基于差商法的嵌入式角位移传感器自标定

孙世政， 何泽银， 董绍江

(1.重庆交通大学 机电与车辆工程学院，重庆 400074；2. 江苏昆山留学人员创业园 博士后科研工作站，江苏 昆山 215300；3. 重庆交通大学 交通运输工程博士后科研流动站，重庆 400074)

基于差商法的嵌入式角位移传感器自标定

孙世政1,2,3， 何泽银1， 董绍江1

(1.重庆交通大学 机电与车辆工程学院，重庆 400074；2. 江苏昆山留学人员创业园 博士后科研工作站，江苏 昆山 215300；3. 重庆交通大学 交通运输工程博士后科研流动站，重庆 400074)

为了摆脱对高精度基准器具的依赖实现对嵌入式角位移传感器的现场标定，结合传感器的结构特点提出了一种利用单个读数头测量值差商的方法实现自我标定。该方法利用傅里叶逼近模型将读数头的误差分离为多次谐波的叠加，采用测量值向前差商的方法获取标定模型的中间变量，运用泰勒展开对差商方法进行了误差估计，并通过提高差商阶数降低模型误差，为了保证标定精度，结合最小二乘算法对标定参数进行了寻优。运用自标定方法对两台不同对极数的嵌入式角位移传感器进行了标定实验，并与传感器常用的比较标定方法进行了对比实验。实验结果表明，两台传感器的误差分别从标定前的±30″和±25″，降低至±2.6″和±2.2″，精度得到了大幅度提高，最终的标定参数与传感器实际的误差成分相吻合，标定精度与比较标定的精度基本相同，能够满足嵌入式角位移传感器的高精度、高效率标定要求。

嵌入式角位移传感器；单读数头；差商法；自标定；标定精度

随着传感器技术的迅速发展，位移传感器在精密机械系统中得到了广泛使用，而如何实现对位移传感器的标定仍是值得研究的问题。传感器的标定过程即为误差校准的过程，误差校准的方法有两类：比较校准和自动校准。比较校准是用高精度的标准仪器与待测仪器进行比较测量实现校准，这种方法被广泛地用于提高仪器和传感器精度。自动校准是利用传感器自身特性来实现对误差的分离，进而实现自我标定。

嵌入式角位移传感器是一种基于电磁感应原理，将被测对象与传感器融合为一体，主要针对机械传动部件的位置检测所研制的新型传感器，由于采用了通过高倍细分和误差修正技术[1-3]，很好地避开了同类传感器精密刻划线的问题，目前该传感器已成功应用于大型车床、铣床等机械主轴回转的位置检测。一般传感器所用的标定方法为比较标定，但在嵌入式角位移传感器的实际应用过程中这种比较标定的方法存在着两个主要问题：①如何不依赖母仪而研制高精度的嵌入式角位移传感器。随着传感器分辨率和原始精度的提高，对校准该传感器的基准仪器的精度要求也相应提高，这就直接制约了高精度角位移传感器的研制；②如何实现传感器的现场直接自动校准。由于受到工作环境、机械参数和电气参数变化的影响，经过标定后的传感器随着时间地推移会出现精度损失的现象，而比较标定的方法难以实现对传感器的现场标定。在这种情况下，迫切需要一种能够实现在现场自我标定的技术[4]。

针对传感器的自标定，国内外的很多学者通过对传感器结构的特殊设计，利用传感器自身的特性来实现对误差的分离和自检，达到自标定的目的。德国物理研究院(Physikalisch Technische Bundesanstalt, PTB)的Probst等[5]研制了一种基于光栅测角仪的高精度转台用于校准角度基准，通过傅里叶分析的方法消除谐波误差，虽然最终精度很高，但仪器结构复杂成本也较高。Masud等[6]开发了一种角度编码器的自动校准系统，通过在主刻度标尺同一圆周不同空间间距设置多个读数头的方法，实现了对角度编码器的自检，这种在整周分布多个读数头的方法对各个读数头的一致 性要求极高，读数头制造和安装的不一致性将直接影响标定的精度。Orton等[7]采用在空气轴承、自由状态下读数头的精确速度来进行自动校准。Lu等[8-9]提出了一种利用光栅脉冲的测量值和精密轴系的动态特性，实现了在单读数头条件下对光栅的分度误差进行自标定的方法。这两种方式的自标定虽然不存在多读数头安装一致性的问题，但标定对精密轴系的动态响应特性有极高的要求。本文结合嵌入式角位移传感器的特点，提出了一种利用单个读数头的误差傅里叶逼近结合测量值差商的标定方法，实现了对嵌入式角位移传感器的误差自标定。实验对比自标定方法与通常的比较标定方法表明，本文构建的自标定系统能够很好地实现对嵌入式角位移传感器高精度、高效率标定。

1 嵌入式角位移传感器

嵌入式位置检测定义为：区别于传统独立传感器的，将传感器嵌入到被测机械系统中，与被测单元融为一体的一种位置检测方式。嵌入式位置检测技术的一个显著优点就是机械系统能够实时检测其自身的工作性能，且信噪比高，结构紧凑。

嵌入式角位移传感器是针对较大尺寸机械传动部件的位置检测所研制的一种新型传感器，其将原有角位移传感器整周封闭的线圈离散成为若干个独立读数头，分布于被测传动部件(尤其适用齿轮、蜗轮)周围，利用被测部件的固有分度来获取运动信息(回转角度)。图1(a)为传统的机械传动部件的位移测量示意图，与这种方法相比，嵌入式角位移传感器采用径向、非接触安装读数头的方式，除了省掉精密传感器和联轴节外，更重要的是它与被测部件融为一体，具有体积小、重量轻、密封好的特点，因此不怕振动、冲击、油污等极端恶劣工况，且更不容易受到空间狭窄、中空和限重等特殊条件的限制，其结构如图1(b)所示。

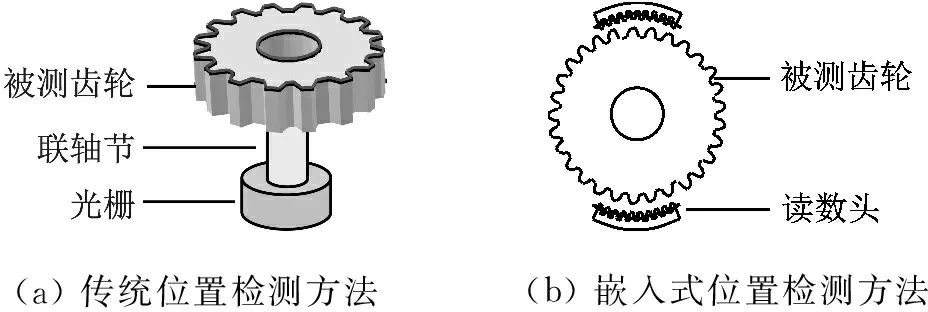
(a)传统位置检测方法(b)嵌入式位置检测方法

图1 嵌入式角位移传感器位置检测与传统位置检测对比

Fig.1 Comparison of embedded angle displacement sensor position detection and traditional position detection

该传感器的工作原理如图2所示，读数头上有两层绕组，分别为激励绕组和感应绕组。当激励绕组通以正弦激励，根据电磁感应原理，感应绕组上会产生同频率的交流信号，当被测部件(转子)相对读数头转动时，空间气隙磁导发生变化，感应信号幅值的大小随着气隙磁导的变化而变化，每转过一个转子齿距，气隙磁导变化一个周期，转过一周，则变化转子齿数个周期，所以转子齿数即为嵌入式角位移传感器的极对数，由于单组感应绕组上产生的信号为驻波信号，故采用两组驻波信号叠加合成的方式形成最终测量用的感应信号，将感应信号与激励信号进行动态鉴相，就可以得到被测部件转动的角位移。

图2 嵌入式角位移传感器工作原理

2 自标定模型

根据误差的定义即误差是测量值和真值之差，可将嵌入式角位移传感器的误差函数可描述为

δ(θ)=f(θ)-θ

(1)

式中：δ(θ)为嵌入式角位移传感器读数头的误差函数；f(θ)为读数头对回转对象的测量值；θ为回转对象角位移的真值。由于真值是无法获知的，虽然这个误差函数是客观存在的，但是无法通过式(1)直接求出。

2.1 傅里叶逼近

嵌入式角位移传感器的测量符合圆周内误差封闭的原则，故可以将误差函数看做以2π为周期的周期函数。根据傅里叶的思想，可以将式(1)中误差函数δ(θ)视为n次误差谐波的叠加，则可表示为[10-12]

(2)

2.2 向前差商法

将式(2)代入式(1)中，两边对测量角度θ求导可得

(3)

f(θn+1)=f(θn)+hf′(θn)+T

(4)

式中：f(θn+1)和f(θn)为相邻的两个测量值；h为标定步长；T为局部截断误差，由此即可使用差商近似导数

(5)

所以，式(3)可表达为

(6)

根据式(6)获得测量值序列{f(θn+1)-f(θn)}的幅度谱{Bn}和相位谱{φn}，则可以得到傅里叶模型中各次谐波的幅值和初相角

(7)

2.3 差商法误差估计与优化

该方法与欧拉法求解一阶常微分方程初值问题的方法不同，差商法中所用的{f(θn+1)-f(θn)}序列为实际测量数据，差商的相邻两值为实际值而非近似值，这就不会产生累积误差。由于利用向前差商的方法代替微分会产生截断误差，将测量值函数Taylor展开

(8)

(9)

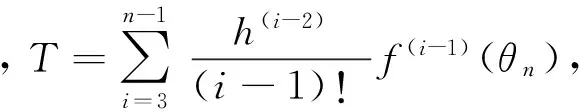
(10)

从式(10)可以明显的看出，在标定步长h较小的情况下，一阶差商、二阶差商和三阶差商产生的截断误差相差并不大；在步长h较大的情况下，提高差商阶数可以有效地降低截断误差。对于提高阶数后的标定，以二阶差商法为例，依次解算出序列{f(θn+1)-f(θn)-hf′(θn)/2}的值。之后便同原理模型中的处理方法一样，利用快速傅里叶获得其幅度谱{Bn}和相位谱{Pn}，进而获得标定所需的参数。三阶差商的方法与二阶相同。

2.4 自标定参数选择

δ(θ)=AL+Δδ(θ)

(11)

式(11)为以幅值和初相位为未知量的方程组，式中n值为谐波次数其值远小于采样点数k，故该方程组为超定方程组，由于测量数据中不可避免地包含有测量误差，待求的参数也必然包含一定的误差，为了提高所得结果的精度，能够抵偿性地减少随机误差的影响，运用最小二乘原理，对方程组进行参数寻优，从低次开始，逐渐增加谐波的次数，以残差平方和为目标，当残差平方和的减少不显著时，解算出n值，同时选取矩阵L和A中对残差影响较大的参数。

3 实验与结果

本文提出的利用单读数头误差的傅里叶逼近结合测量值差商的自标定方法，在嵌入式角位移传感器的标定系统上进行了实验验证。标定系统以精密的分度转台作为测量对象，对比实验中的基准器具采用是德国海德汉高精度光栅，通过弹性联轴结将嵌入式角位移传感器和光栅安装在分度转台的主轴上，控制系统通过驱动电机带动转台做匀速转动的同时，光栅和角位移传感器对分度转台转过的角度进行同步测量。误差数据的采集是动态过程，其对速度的变化比较敏感，为了得到相对恒定的转速，本系统利用光栅将位置信息反馈给运动控制卡形成闭环的控制方式，达到了较高的控制精度。图3为嵌入式角位移传感器自标定实验系统框图。

3.1 模型参数寻优

以24对极的嵌入式角位移传感器为例，分析模型参数的寻优过程。角位移传感器常用的标定速度为0.1 r/min和0.5 r/min，系统的采样频率为400 Hz，在0.1 r/min和0.5 r/min的情况下的标定步长分别为5″和25″。在标定步长一定的情况下，不同阶数差商的截断误差如下图4和图5所示。

图4中在标定速度相对较低步长较小的情况下，一阶、二阶和三阶差商的截断误差较小，误差在0.005″以内，一阶差商的截断误差为0.004 6″，二阶为0.003 5″，三阶为0.003″，各阶之间相差不大；图5中在标定步长较大的情况下，一阶差商的截断误差为0.45″，二阶为0.046″，三阶为0.04″，二阶和三阶差商的截断误差差异不大，但明显比一阶差商误差小；由于传感器的原始误差较大，最终的标定精度数量级通常为0.1″，故两种标定步长下二阶和三阶差商的截断误差对标定精度影响不大，但考虑到标定效率的问题，采用步长为25″，差商阶数为二阶，能更为有效地提高标定效率。

图3 嵌入式角位移传感器自标定实验系统

(a)

(b)

(c)

(a)

(b)

(c)

为了保证标定精度，利用最小二乘算法对标定参数进行寻优，根据式(11)，从低次开始，逐渐增加谐波的次数，直到残差平方和的减少不显著，解算出矩阵A中的谐波次数、相位角和矩阵X。标定参数寻优效果图如下图6所示，表1为寻优后得到的标定参数。

图6 标定参数寻优

表1 自标定参数表

从图6中可以看到，当n=78 时残差平方和的减少不再显著。从标定参数表1中可以看出，谐波幅值较大的为48次和24次，这种短周期的误差主要是由激励正交性和绕线一致性不好引起的，由于转子加工所导致的个别齿有瑕疵，将会产生短周期附带误差，即表中的51次、69次等，传感器使用过程中的安装偏心将会引起长周期1次和2次误差，由此可见，最终的参数寻优结果与传感器实际的误差成分相符合。

根据傅里叶逼近模型，各次谐波的幅值越大表明其在误差中的比重越大，在标定时需要把这些幅值较大的误差谐波补偿到测量值中。对于幅值较小的误差谐波，通常认为幅值小于0.5的误差谐波较小，可以在标定中进行忽略。通过参数寻优后得到了各次主要误差谐波的谐波次数、幅值和初相位，依据傅里叶逼近模型，将这些参数代入到式(2)中，就可以实现对误差函数的重构，在传感器标定过程中，通过误差函数可以得到误差值，将测量值和误差值相加就实现了对传感器的标定。

3.2 传感器自标定

为了验证本文标定方法的有效性和可靠性，共对两种类型嵌入式角位移传感器进行了独立自标定实验，图7为24对极嵌入式角位移传感器的标定结果，图8为18对极嵌入式角位移传感器的标定结果。

(a)标定前(b)标定后

图7 24对极嵌入式角位移传感器的标定结果

图8 18对极嵌入式角位移传感器的标定结果

Fig.8 Result of self-calibration for 18 polars embedded angle displacement sensor

图7中的传感器经过自标定后原始误差从±30″降至±2.6″，图8中的传感器经过自标定后原始误差从±25″降至±2.2″，可以看出该自标定方法可以有效地降低了原始误差。

3.3 标定对比实验

为了验证自标定方法的正确性，与比较标定方法进行了对比实验，分别用自标定方法和比较标定方法对24对极和18对极嵌入式角位移传感器进行了标定对比实验。两种标定方法最终精度对比结果如图9和图10所示。

(a)自标定(b)比较标定

图9 24对极两种标定方法最终精度对比

Fig.9 Comparison of self-calibration and standard implement calibration for 24 polars

从图9和图10可以看出，两种标定方法的最终精度范围基本相同，表明该自标定方法正确有效。与通常的传感器比较标定的方法相比，该方法能够在保证标定精度的情况下实现脱离基准器具的现场标定，与多个读数头自标定的方法相比，该方法可以避免由于读数头不一致所引入的误差，同时可以实现对多个读数头的分别标定。

(a)自标定(b)比较标定

图10 18对极两种标定方法最终精度对比

Fig.10 Comparison of self-calibration and standard implement calibration for 18 polars

4 结 论

本文针对嵌入式角位移传感器提出了一种利用单个读数头实现自我标定的标定方法。该方法利用傅里叶逼近模型将误差分解为多次谐波的叠加，利用测量值的向前差商获取标定模型的中间变量，通过提高差商阶数降低模型误差，运用最小二乘算法对最终的标定参数进行寻优。运用该标定方法对两台嵌入式角位移传感器进行了标定和对比实验，结果表明两台传感器的误差由标定前的±30″左右降至标定后±2.5″左右，精度有了大幅度提高，参数寻优后得到的标定参数与传感器实际的误差成分相吻合，标定精度与以往母仪标定的精度基本相同，对嵌入式角位移传感器脱离基准器具实现现场标定具有较高的指导价值。

[1] GUMAROV S G，KORSUN O A. A method of determining the dynamic error of optical trajectory measurement stations[J]. Measurement Technique, 2011,54(3):281-286.

[2] 高策, 乔彦峰. 光电经纬仪测量误差的实时修正[J]. 光学精密工程, 2007, 15(6)：846-851.

GAO Ce, QIAO Yanfeng. Real-time error-correction method for photoelectrical theodolitet[J]. Optics and Precision Engineering, 2007, 15(6)：846-851.

[3] 高贯斌, 王文, 林铿, 等. 圆光栅角度传感器的误差补偿及参数辨识[J].光学精密工程, 2010, 8(18)：1766-1772.

GAO Guanbin, WANG Wen, LIN Keng, et al. Error compensation and parameter identification of circular grating angle sensors[J]. Optics and Precision Engineering, 2010, 8(18)：1766-1772.

[4] 郭士旭, 余尚江, 陈晋央,等. 压电式压力传感器动态特性补偿技术研究[J]. 振动与冲击, 2016, 35(2): 136-140.

GUO Shixu, YU Shangjiang, CHEN Jinyang, et al. Dynamic compensation technique for piezoelectric pressure sensors[J]. Journal of Vibration and Shock, 2016, 35(2): 136-140.

[5] PROBST R, WRITTEKONF R, KRAUSE M, et al. The new PTB angle comparator[J].Measure Science Technology,1998,9(7):1059-1066.

[6] MASUD A, KAJITANI P. An automatic calibration system for angular encoders[J]. Precision Engineering, 1989, 11(2)：95-100.

[7] ORTON P A, POLIAKOFF J F, HATIRIS E, et al. Automatic self-calibration of an incremental motion encoder[J]. Instrument Measure Technology, 2001,8(6):1617-1618.

[8] LU X D, TRUMPER D L. Self-calibration of on-axis rotary encoders[J]. Annals of the CIRP, 2007, 56(1)：499-504.

[9] LU X D, GRAETZ R, AMIN-SHAHIDI D, et al.On-axis self-calibration of angle encoders[J].CIRP Annals Manufacturing Technology, 2010,59(1)：529-534.

[10] 彭东林, 刘小康, 张兴红, 等. 基于谐波修正法的高精度时栅位移传感器[J]. 仪器仪表学报, 2006, 27(1)：31-33.

PENG Donglin, LIU Xiaokang, ZHANG Xinghong, et al. High-precision time-grating displacement sensor based on harmonic wave correcting method[J]. Chinese Journal of Scientific Instrument, 2006, 27(1)：31-33.

[11] 张宁, 沈湘衡, 杨亮, 等. 利用动态靶标谐波特性评价光电经纬仪的跟踪性能[J].光学精密工程, 2010, 18(6)：1286-1293.

ZHANG Ning, SHEN Xingheng, YANG Liang, et al. Evaluation of tracking performance of photoelectric theodolite by using harmonic property of dynamic target[J]. Optics and Precision Engineering, 2010, 18(6)：1286-1293.

[12] 于梅. 低频振动传感器幅值和相移测量的不确定度[J]. 振动与冲击, 2009, 28(4): 106-110.

YU Mei. Uncertainty of measurement of amplitude and phase shift of low frequency vibration sensor[J]. Journal of Vibration and Shock, 2009, 28(4): 106-110.

Self-calibration for embedded type angle displacement sensors based on difference quotients

SUN Shizheng1,2,3, HE Zeyin1, DONG Shaojiang1

(1.School of Mechatronics and Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, China; 2. Post-doctoral Research Station, Kunshan Business Incubator for Overseas Chinese Scholars, Kunshan 215300, China; 3. Traffic and Transportation Post-doctoral Research Station, Chongqing Jiaotong University, Chongqing 400074, China)

In order to get rid of the dependence on high precision reference and realize field calibration of an embedded type angle displacement sensor, a self-calibration method was proposed using difference quotients of measured values obtained with a discrete probe. With the proposed method, the error function of the probe was separated into multiple harmonics with Fourier approaching model. The forward difference quotient of measured values was used to get intermediate variable of the calibration model. Taylor expansion was applied to estimate errors of difference quotients, the calibration model errors were reduced through increasing the order of difference quotient. To ensure the calibration precision, the least squares algorithm was used to optimize calibration parameters. Two embedded type angle displacement sensors with different pairs of poles were calibrated using the proposed method. The results were compared with those using the traditional comparative calibration method. The actual calibration tests showed that the errors of the two sensors are reduced from ±30″ and ±25″, respectively to ±2.6″ and ±2.2″, respectively; the final calibration parameters are consistent with the actual sensors’ error components; the self-calibration precision is almost the same as the accuracy of the comparative calibration, the former can meet embedded type angle displacement sensors’ calibration requirements.

embedded type angle displacement sensor; discrete probe; difference quotient algorithm; self-calibration; calibration precision

国家自然科学基金资助(51405047)；重庆市教委科学技术(KJ1600534；KJ1600503)；重庆市基础科学与前沿技术研究(CSTC2016JCYJA0514)

2016-05-23 修改稿收到日期：2016-10-27

孙世政 男，博士，讲师，1986年生

何泽银 男，博士，副教授，1985年生

TP212.6

A

10.13465/j.cnki.jvs.2017.13.039