一种负泊松比正弦曲线蜂窝结构的面内冲击动力学分析

邓小林， 刘旺玉

(华南理工大学 机械与汽车工程学院,广州 510640)

一种负泊松比正弦曲线蜂窝结构的面内冲击动力学分析

邓小林， 刘旺玉

(华南理工大学 机械与汽车工程学院,广州 510640)

研究了一种全参数化的正弦曲线蜂窝结构，通过Pro/Engineer构建了其参数化模型，采用ABAQUS建立了正弦曲线蜂窝结构的有限元模型。研究了不同振幅、不同胞壁厚度的正弦曲线蜂窝结构在不同冲击速度下的面内动力学响应。研究表明，正弦曲线蜂窝结构的反作用力波动情况与其振幅以及冲击速度直接相关。振幅越小、蜂窝结构胞壁越厚，其反作用力波动越明显。速度越高，蜂窝结构的反作用力波动越明显。而振幅较大的正弦曲线蜂窝结构，在不同的速度下，其反作用力表现出了较好的稳定性。正弦曲线蜂窝结构固定端的平台应力主要与其厚度有直接关系，与冲击速度无关。通过对正弦曲线蜂窝结构的能量吸收情况分析表明，随着振幅的增加，其能量吸收能力相对下降，随着速度的提高，蜂窝结构能量吸收能力趋向于一致。结果表明，正弦曲线蜂窝结构的轻微拉胀效应可增强其平面内能量吸收能力，相对普通的常规正六边形蜂窝结构，具有更好的能量吸收效果。

负泊松比；正弦曲线；蜂窝结构；面内冲击

汽车被动安全性当中的碰撞安全已成为目前国内外研究的热点，对以耗散碰撞动能的能量吸收结构和材料的相关研究越来越受到重视[1]。蜂窝结构，在能量耗散过程中具有行程长、质量轻，能够在保持稳定平台应力水平下吸收大量冲击动能的特点，具有十分广阔的应用前景[2-3]。针对蜂窝结构的冲击响应的相关分析已经很多，包括面内冲击[4-6]、面外冲击[7-8]、非规则的蜂窝结构冲击[9-11]、蜂窝结构参数优化[12-13]等等，但现有的研究主要集中在常规的正泊松比蜂窝结构的研究和分析方面。

负泊松比材料，也称之为拉胀材料(Auxetic Materials)，与普通正泊松比材料在拉伸时垂直于拉伸方向变窄，压缩时垂直于压缩方向变宽的原理恰恰相反，指的是当材料拉伸时，垂直于拉伸方向变宽，而压缩时垂直于压缩方向变窄。1944年Love[14]在其专著当中对负泊松比进行了描述，这是有记录可查的最早对负泊松比进行描述的论著。虽然自然界早就存在着天然的拉胀材料，但并没有引起太多的关注，直到Lakes[15]在1987年通过用常规的开孔泡沫材料制造出了一种各向同性的负泊松比泡沫材料。自此以后，针对拉胀材料相关研究开始快速发展起来，各种各样不同形式的拉胀结构被不断的设计和研究出来[16-17]。但现有的针对拉胀材料的研究工作主要集中在拉胀材料的拓扑结构以及力学性能和负泊松比变形机制的相关研究上，而引入负泊松比的吸能结构的相关研究，才刚刚开展[18-21]。与正泊松比结构不同的是，负泊松比结构在受到单向冲击压缩时，横向会产生收缩变形，相对传统正泊松比结构，负泊松比结构将具有更好的抗压效果与能量吸收性能。如：杨德庆等[22]利用有限元计算对金属铝拉胀网格蜂窝芯层合板与普通铝蜂窝芯层合板进行了平面内子弹撞击试验仿真，结果显示拉胀蜂窝芯层合板具有更好的平面内抗侵彻性能，这种优势性能被归结于侵彻体前段的拉胀网格受压致密化现象，而这种现象正是直接由其负泊松比特性决定。Schultz等[23]以平面内冲击能量为优化目标，对多孔蜂窝结构的结构参数进行了优化，优化结果表明轻微的拉胀结构与倾斜的蜂窝壁可以获得最大的平面内能量吸收。因此，针对负泊松比材料与能量吸收相关的研究，具有重要的现实意义和研究价值。

2007年Doll等[24]提出了一种正弦曲线凹角结构，提出了这种结构具有负泊松比效应，将该结构旋转成圆柱状用于药物洗脱支架的设计上，与常规的菱形圆柱支架进行了对比，得出了比常规菱形支架更高的周向强度。但将该结构设计成一平面正弦曲线蜂窝结构，及对结构的面内冲击下的力学性能的相关研究并没有涉及。正弦曲线蜂窝结构是一种具有负泊松比效应的结构，其相对常规的负泊松比结构而言，具有结构参数少，各结构参数之间具有关联性等特点，容易通过参数关系来实现整个蜂窝结构模型的全参数化控制和不同结构的蜂窝结构自动化生成等优点。因此，有必要对正弦曲线蜂窝结构进行系统研究和分析。然而，除了Doll等之外，目前没有发现有针对正弦曲线蜂窝结构的相关研究和报道。基于上述原因，本论文拟对正弦曲线蜂窝结构的几何结构以及面内冲击下的不同胞壁厚度、不同冲击速度和不同振幅下的动力学响应进行系统研究，为正弦曲线蜂窝结构的后续研究提供基础。

1 分析模型

1.1 正弦曲线蜂窝的几何结构

图1 正弦曲线蜂窝几何结构图

为了对比分析不同拉胀程度的蜂窝结构面内冲击效应，这里将振幅A设为变量，通过采用Pro/Engineer软件建立了该正弦曲线蜂窝结构的全参数化模型，输入不同的振幅和曲线的阵列数量，即可全自动的生成新的正弦曲线蜂窝结构。

1.2 相对密度

蜂窝材料和泡沫材料的性能主要取决于它们的相对密度，根据相对密度的定义，正弦曲线蜂窝结构的相对密度可表示为

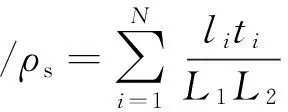
(1)

式中：ρ*为蜂窝结构的表观密度；ρs为构成蜂窝结构的材料的密度；N为正弦曲线的数量；li为第i根曲线的长度；ti为第i根曲线的厚度；L1，L2为整个蜂窝结构的长度和宽度。

通过数值方法计算出单根曲线的长度后，即可通过式(1)求得不同振幅和壁厚的蜂窝结构的相对密度。本论文主要研究不同振幅的正弦曲线蜂窝结构，通过改变正弦曲线的振幅，可得到不同的负泊松比。这里，主要对A分别取0.5 mm、1 mm、1.25 mm、1.5 mm四种不同拉胀效应的蜂窝结构进行对比分析，求得的相对密度如表1所示。

1.3 有限元模型

论文主要采用ABAQUS软件来进行动力学模型分析。图2所示即为常规正六边形蜂窝结构和正弦曲线蜂窝结构冲击模型示意图。考虑到正弦曲线在ABAQUS里建模困难，这里利用Pro/Engineer软件强大的三维参数化建模能力，先在Pro/Engineer软件里对蜂窝结构的三维模型进行构建，然后通过STP中间格式文件导入ABAQUS软件进行模拟仿真。蜂窝结构的面外厚度统一为1.5 mm。材料采用金属铝，并假设其为理想弹塑性模型，密度ρ=2 700 kg/m3、杨氏模量E=69 Gpa、泊松比u=0.3、屈服应力σy=76 Mpa。模型采用四节点减缩积分壳单元进行模拟，单元平均长度为0.5 mm，为了保证收敛，沿厚度方向采用5个积分点。上下刚体均采用解析刚体，边界条件与文献[4,20-21]一致，即固定端刚体与蜂窝结构采用绑定约束，并将固定端刚体固定，冲击端刚体与蜂窝结构采用面面接触，摩擦系数取0.2。为防止压缩后的蜂窝结构穿透刚体，模型施加单面自动接触算法。约束蜂窝结构的所有面外位移以确保结构在冲击过程中不发生面外弯曲。冲击端刚体以恒定冲击速度对蜂窝结构进行冲击，冲击压缩距离为初始长度的80%。为了对比分析不同速度下蜂窝结构的响应，采用了不同的几组速度分别对其进行了仿真模拟。

表1 不同蜂窝壁厚度t与振幅A的相对密度表

(a)

(b)

1.4 平台应力及能量吸收相关概念

名义应力的基本计算公式如下

(2)

式中：σ为名义应力；F为固定端刚体与蜂窝结构之间的接触力；L为蜂窝结构水平面长度；b为面外方向的厚度。通过式(2)可知，名义应力即为蜂窝结构所受到的冲击除以蜂窝结构与底面刚体的接触面积。

蜂窝结构的平台应力可表示为

(3)

式中：ε0为对应于初始峰值应力的名义应变；εd为锁定应变，为蜂窝结构密实化阶段的所对应的应变。

εd一般由式(4)确定

(4)

2 数值模拟结果及讨论

2.1 正弦曲线蜂窝结构变形模式

正弦曲线蜂窝结构面内冲击下的变形模式如图3所示。其中模型参数为：A=1.5 mm、t=0.2 mm、υ=10 m/s。通过图3可知，在冲击的起始阶段，随着压缩的进行，冲击端的蜂窝由于结构本身的负泊松比效应，整个结构发生了横向收缩。当名义压缩应变增加到ε=0.2时，固定端开始出现变形，横向收缩现象更为明显。随着压缩的不断增加，变形由冲击端不断向固定端传播开来，固定端的中间部分也开始由下往上开始变形，整个正弦曲线蜂窝结构开始变成较为规则的菱形形状。当名义压缩应变达到ε=0.53时，菱形的蜂窝结构也开始逐渐被压溃，压溃的部分形成了一种倒“X”形状。当压缩到ε=0.67时，整个形状被压缩成“一”字形形状，中间部分被全部压溃。从ε=0.67到ε=0.8阶段，冲击端到中间部分被一层一层的全部压溃，而固定端部分并没有被完全压实，这主要是因为在有限元模型构建的时候，将固定端的蜂窝结构与固定刚体绑定了起来，导致整个固定端的蜂窝结构整体抗冲击能力增加所致。若固定端的蜂窝结构与固定刚体不绑定，变形将稍有不同，考虑到主要采用横向对比，这里边界条件采用了与文献[4,20-21]一致的设置。

(a) ε=0.08

(b) ε=0.2

(c) ε=0.4

(d) ε=0.53

(e) ε=0.67

(f) ε=0.8

2.2 正弦曲线蜂窝结构在不同速度冲击下的变形模式

蜂窝结构在不同速度的冲击下，其变形模式具有较大的差别。这里分别取A为0.5 mm、1 mm、1.5 mm，υ为3 m/s、10 m/s、20 m/s、50 m/s进行对比分析。所有结构的t=0.2 mm，取变形量为ε=0.4时的变形模式如图4所示。

(a1) υ=3 m/s；A=0.5 mm

(a2) υ=3 m/s；A=1 mm

(a3) υ=3 m/s；A=1.5 mm

(b1) υ=10 m/s；A=0.5 mm

(b2) υ=10 m/s；A=1 mm

(b3) υ=10 m/s；A=1.5 mm

(c1) υ=20 m/s；A=0.5 mm

(c2) υ=20 m/s；A=1 mm

(c3) υ=20 m/s；A=1.5 mm

(d1) υ=50 m/s；A=0.5 mm

(d2) υ=50 m/s；A=1 mm

(d3) υ=50 m/s；A=1.5 mm

当υ=3 m/s，因为速度相对较小，整个变形模式首先从冲击端开始。压缩量达到ε=0.4时，A的取值不同，其变形模式有很大区别。A=0.5 mm的蜂窝结构，其冲击端和固定端往上的几层蜂窝都已经被压溃，而中间部分并没有发生明显的变化。A=1.5 mm的蜂窝结构，整个蜂窝结构能看到明显的横向收缩现象，并且整个蜂窝结构被压成了近乎均匀的菱形形状。A=1 mm的蜂窝结构变形则介于A=0.5 mm和A=1.5 mm这两种蜂窝结构之间，冲击端的蜂窝结构由菱形形状和压溃的菱形混合组成。固定端靠近底部出现了压溃现象，底部往上中间部分变成了菱形形状，蜂窝结构的中间部分没有发生明显的变形。说明A=1.5 mm的蜂窝结构其变形比较均匀，A=0.5 mm的蜂窝结构其冲击波动较大。

当υ=10 m/s时，由于惯性效应，A=0.5 mm的蜂窝结构开始从冲击端逐层压溃，固定端没有发生任何变形和压溃的现象。A=1 mm的蜂窝结构也从冲击端往下压溃，整个蜂窝结构的横向收缩较为明显，而固定端并没有发生变形。A=1.5 mm的蜂窝结构仍然表现出较好的均匀性，整个蜂窝结构被压成了较为均匀的菱形形状。

随着速度的增加，惯性效应增强，当速度达到υ=50 m/s，A=0.5 mm的蜂窝结构变形表现为从冲击端逐层压溃，显示出了与常规蜂窝结构材料相一致的变形模式。A=1.5 mm的蜂窝结构虽然还能看到结构由于负泊松比效应所产生的横向收缩现象，但固定端已经没有变形。

从上述分析可知，正弦蜂窝结构的变形模式与冲击速度和振幅A值有很大的关系。负泊松比越明显的蜂窝结构，其变形相对均匀，波动较小，变形较为平稳。

2.3 不同振幅正弦曲线蜂窝结构的动力响应曲线

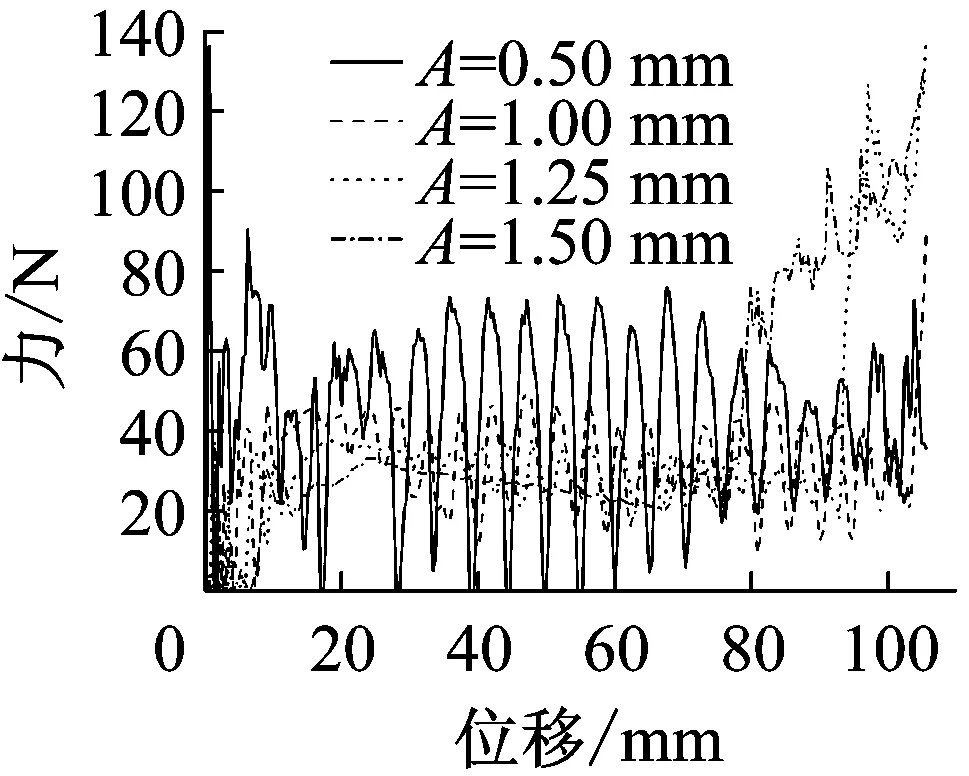
图5和图6是胞壁厚度t=0.2 mm，不同振幅的正弦曲线蜂窝结构分别在υ=10 m/s和υ=20 m/s冲击时，固定端和冲击端的响应曲线。

图5(a)为不同振幅正弦曲线蜂窝结构在υ=10 m/s时固定端的反作用力和位移曲线。通过该图可知，A=0.5 mm的正弦曲线蜂窝结构，其固定端的反作用力波动非常明显，从到达初始蜂值应力开始，一直到压缩距离达到66 mm左右，即ε=0.4时，反作用力才逐渐趋于稳定，具有较大的波动。A=1 mm的正弦曲线蜂窝结构，与普通的多胞材料一样，冲击力到达平均冲击力附近时上下波动，直到最后进入密实化阶段，其变形机制与普通的蜂窝结构材料基本一致。

A=1.25 mm和A=1.5 mm的正弦曲线蜂窝结构，固定反作用力都有一个明显的提高阶段，这主要是因为它们的变形模式引起。平台区的前半部分的变形主要是由正弦曲线被压成菱形状，其作用力相对较小。随着压缩的进行，当ε=0.4，即压缩距离达到66 mm左右时，蜂窝结构开始由菱形逐渐被压溃，平台应力开始有较大提高。A=1.5 mm的正弦曲线蜂窝结构变化相对平稳。A=1.25 mm的正弦曲线蜂窝结构在后半部分有一个突然提高，这主要是因为A=1.25 mm的正弦曲线蜂窝结构在被完全压缩成菱形结构前，靠近冲击端的蜂窝开始被压溃所致。

图5(b)为υ=20 m/s时的响应曲线，其固定端反作用力和位移曲线与υ=10 m/s时的蜂窝相比，由于惯性效应的增强，各种不同振幅的正弦曲线蜂窝结构反作用力的波动都有所提高，其中A=0.5 mm的蜂窝结构的波动最为激烈。A=1.25 mm的蜂窝结构由于冲击速度的增加，其第一个平台区出现了增长，在压缩距离达到92 mm时，平台应力出现了大幅度的增加，快速进入了压实阶段。尽管速度增加，但A=1.5 mm的蜂窝结构相对υ=10 m/s速度，平台应力并没有出现很大的波动，只有在蜂窝结构由菱形逐渐被压溃时，其反作用力波动较大，主要是因为速度的增加，菱形结构被压溃和坍塌所致。

图6为胞壁厚度t=0.2 mm，不同振幅的蜂窝结构分别在υ=10 m/s和υ=20 m/s冲击时，冲击端的响应曲线。通过对比分析图5和图6可知，冲击端的反作用力与固定端的反作用力具有基本一致的趋势，但冲击端波动相对于固定端的反作用力更为明显，尤其在冲击开始的一瞬间，具有一个很大的冲击反力。振幅越小的蜂窝结构，波动情况越明显。

(a) υ=10 m/s

(b) υ=20 m/s

图5 不同振幅蜂窝结构固定端在υ=10 m/s和υ=20 m/s冲击时力和位移曲线(t=0.2 mm)

Fig.5 Dynamic force-displacement curves of honeycombs with different amplitude under 10 m/s andυ=20 m/s impact velocities at the supporting end

(a) υ=10 m/s

(b) υ=20 m/s

图6 不同振幅蜂窝结构冲击端在υ=10 m/s和υ=20 m/s冲击时力和位移曲线(t=0.2 mm)

Fig.6 Dynamic force-displacement curves of honeycombs with different amplitude under 10 m/s andυ=20 m/s impact velocities at the impacting end

为了对比分析不同厚度的正弦曲线蜂窝结构在不同速度冲击下的固定端的响应情况，这里对振幅A=1 mm和A=1.25 mm的正弦曲线蜂窝结构分别在t=0.1 mm、t=0.2 mm、t=0.3 mm、t=0.4 mm、t=0.5 mm五种不同厚度，υ=3 m/s、υ=10 m/s、υ=20 m/s三种不同速度下的冲击响应情况进行了分析，分析结果如图7所示。通过分析图7可知，平台应力主要与蜂窝结构的厚度直接有关，随着厚度的增加，平台应力明显增加，但随着速度的增加，固定端的平台应力基本保持不变，其结果与文献[21]所分析的结果一致。

(a) A=1 mm

(b) A=1.5 mm

2.4 正弦曲线蜂窝结构的能量吸收特征

评价结构能量吸收的最重要指标为材料单位质量吸能的能量，其表达式可表示为[25]

(5)

式中：Eint为结构的能量吸收；m为结构的质量。

而结构的能量吸收Eint又可表示为

(6)

根据式(2)中Δρ=ρ*/ρs得

m=ρ*v=Δρ×ρs×(L×L×b)

(7)

将式(6)和式(7)代入式(5)可得

(8)

这里，将常规正六边形蜂窝与具有负泊松比效应的正弦曲线蜂窝结构进行对比分析，研究正弦曲线蜂窝结构的能量吸收特征。蜂窝结构的最重要参数为其相对密度，而四种不同振幅的正弦曲线蜂窝结构的相对密度分别为：0.033 897 475、0.035 512 121、0.036 658 081、0.037 994 697。取其平均值0.036作为对比分析的正六边形蜂窝结构的相对密度。根据正六边形蜂窝结构的相对密度方程

(9)

(10)

根据式(10)即可求得所设计的正六边蜂窝结构的边长为3.2mm。其结构如图2所示。采用与正弦曲线完全相同的数值分析和设置条件对其进行仿真对比分析。图8所示即为胞元壁厚为0.1mm时，常规正六边形蜂窝结构和不同振幅的正弦曲线蜂窝结构在不同冲击速度下的单位质量能量吸收情况。

(a) υ=10 m/s

(b) υ=20 m/s

(c) υ=50 m/s

(d) υ=120 m/s

通过图8可知，当υ=10 m/s时，在压缩应变ε=0.2之前，常规正六边形蜂窝结构的能量吸收好于正弦曲线蜂窝结构的能量吸收。但随着压缩的进行，正弦曲线蜂窝结构的负泊松比效应导致的横向收缩，使得振幅A=0.5 mm的正弦曲线蜂窝结构的单位能量吸收性能逐渐超过常规正六边形蜂窝结构。而A=1 mm和A=1.5 mm两种正弦曲线蜂窝结构由于在压缩初始阶段变为菱形阶段能量吸收相对较少，再加上A=1 mm和A=1.5 mm两种正弦曲线蜂窝结构本身质量相对较大，导致其整体单位能量吸收情况较低。该结论也与Schultz等的轻微拉胀结构与倾斜的蜂窝壁可以获得最大的平面内能量吸收的结论相一致。υ=20 m/s时的能量吸收情况总体上与υ=10 m/s保持一致。但随着速度的增加，其变形模式逐渐演成为由冲击端向固定端孔壁的逐层坍塌，在υ=120 m/s时，常规六边形蜂窝结构的能量吸收已经始终高于正弦曲线蜂窝结构。这也主要是由于正弦曲线的蜂窝结构在没有完全横向收缩之前即已经从冲击端被逐层压溃。值得指出的是，振幅较小的蜂窝结构，其能量吸收曲线呈现波浪形上升，而振幅较大的蜂窝结构，其能量吸收曲线几乎是以直线的形式上升，也说明了振幅较小的蜂窝结构波动较为剧烈。振幅较小的蜂窝结构其单位能量吸收性能相对振幅较大的蜂窝结构要好。速度越大，其能量吸收越多，并且随着速度的增加，惯性效应增强，不同蜂窝结构的单位质量能量吸收逐渐趋向于一致。通过上述分析可看出，蜂窝结构的轻微拉胀效应可增强其平面内能量吸收能力，相对普通的常规蜂窝结构，具有更好的能量吸收效果。

3 结 论

论文对不同振幅、不同厚度的正弦曲线蜂窝结构在不同速度冲击下的面内动态冲击特性进行了分析和研究。研究结果表明，不同振幅的正弦曲线蜂窝结构，变形模式有较大差异，振幅越少、速度越高，固定端的反作用波动较大。振幅较大的蜂窝结构，其平台应力在初始阶段较低，在压缩的后半程阶段出现了一个较大的提高，随着速度的增加，其平台应力并没有出现较大的波动情况，表现出了较好的稳定性。论文对不同厚度的蜂窝结构在不同速度冲击下的响应情况进行了分析，蜂窝结构固定端的平台应力主要与其厚度有直接关系，与其冲击速度无关。通过对蜂窝结构的能量吸收情况分析表明，随着振幅的增加，其能量吸收能力相对下降，高速冲击时，不同的正弦曲线蜂窝结构在不同压缩阶段能量吸收能力趋向于一致，而轻微拉胀效应的正弦曲线蜂窝结构比常规蜂窝结构能量吸收能力更好。

[1] JOHNSON W, REID S R. Metallic energy dissipating systems[J]. Applied Mechanics Reviews, 1978, 31(3): 277-288.

[2] GIBSON L J, ASHBY M F. Cellular solids: structure and properties[M].2nd ed. Cambridge: Cambridge University Press,1977：5-35.

[3] 张新春，刘颖，张建辉.金属蜂窝材料的面内冲击响应和能量吸收特[J].功能材料，2013，44(15)：2143-2147.

ZHANG Xinchun，LIU Ying，ZHANG Jianhui. In-plane crushing response and energy absorption characteristics of metal honeycombs[J]. Functional Materials，2013，44(15)：2143-2147.

[4] RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs—a finite element study[J]. International Journal of Impact Engineering, 2003, 28(2): 161-182.

[5] DEQIANG S, WEIHONG Z. Mean in-plane plateau stresses of hexagonal honeycomb cores under impact loadings[J]. Composite Structures, 2009, 91(2): 168-185.

[6] SUN D, ZHANG W, ZHAO Y, et al. In-plane crushing and energy absorption performance of multi-layer regularly arranged circular honeycombs[J]. Composite Structures, 2013, 96(4): 726-735.

[7] XU S, BEYNON J H, RUAN D, et al. Experimental study of the out-of-plane dynamic compression of hexagonal honeycombs[J]. Composite Structures, 2012, 94(8): 2326-2336.

[8] DEQIANG S, WEIHONG Z, YANBIN W. Mean out-of-plane dynamic plateau stresses of hexagonal honeycomb cores under impact loadings[J]. Composite Structures, 2010, 92(11): 2609-2621.

[9] ZHENG Z, YU J, LI J. Dynamic crushing of 2D cellular structures: a finite element study[J]. International Journal of Impact Engineering, 2005, 32(1): 650-664.

[10] LI K, GAO X L, WANG J. Dynamic crushing behavior of honeycomb structures with irregular cell shapes and non-uniform cell wall thickness[J]. International Journal of Solids and Structures, 2007, 44(14): 5003-5026.

[11] LIU Y D, YU J L, ZHENG Z J, et al. A numerical study on the rate sensitivity of cellular metals[J]. International Journal of Solids and Structures, 2009, 46(22): 3988-3998.

[12] XIE S, ZHOU H. Analysis and optimization of parameters influencing the out-of-plane energy absorption of an aluminum honeycomb[J]. Thin-Walled Structures, 2015, 89: 169-177.

[13] HE Q，MA D W. Parametric study and multi-objective crashworthiness optimization of reinforced hexagonal honeycomb under dynamic loadings[J]. International Journal of Crashworthiness，2015，5：1-15.

[14] LOVE A E H. A treatise on the mathematical theory of elasticity[M]. Cambridge: Cambridge University Press, 2013.

[15] LAKES R. Foam structures with a negative Poisson’s ratio[J]. Science, 1987, 235: 1038-1040.

[16] CARNEIRO V H, MEIRELES J, PUGA H. Auxetic materials—a review[J]. Materials Science-Poland, 2013, 31(4): 561-571.

[17] PRAWOTO Y. Seeing auxetic materials from the mechanics point of view: a structural review on the negative Poisson’s ratio[J]. Computational Materials Science, 2012, 58: 140-153.

[18] QIAO J X，CHEN C Q. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs[J].International Journal of Impact Engineering，2015，83：47-58.

[19] ZHANG X C, AN L Q, DING H M, et al. The influence of cell micro-structure on the in-plane dynamic crushing of honeycombs with negative Poisson’s ratio[J]. Journal of Sandwich Structures and Materials，2014，17(1):26-55.

[20] 卢子兴，李康.四边手性蜂窝动态压溃行为的数值模拟[J].爆炸与冲击，2014，34(2):181-187.

LU Zixing，LI Kang. Numerical simulation on dynamic crushing behaviors of tetrachiral honeycombs[J]. Explosion and Shock Waves，2014，34(2):181-187.

[21] 张新春，刘颖，李娜.具有负泊松比效应蜂窝材料的面内冲击动力学性能[J].爆炸与冲击，2012，32(5)：475-482.

ZHANG Xinchun，LIU Ying，LI Na. In-plane dynamic crushing of honeycombs with negative Poisson’s ratio effects[J]. Explosion and Shock Waves，2012，32(5)：475-482.

[22] 杨德庆, 马涛, 张梗林. 舰艇新型宏观负泊松比效应蜂窝舷侧防护结构[J]. 爆炸与冲击, 2015, 35(2):243-248.

YANG Deqing，MA Tao，ZHANG Genglin. A novel auxetic broadside defensive structure for naval ships[J]. Explosion and Shock Waves，2015，35(2)：243-248.

[23] SCHULTZ J, GRIESE D, SHANKAR P, et al. Optimization of honeycomb cellular meso-structures for high speed impact energy absorption[C]∥2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. [S.l.]: ASME, 2011:955-965.

[24] DOLLA W J, FRICKE B A, BECKER B R. Structural and drug diffusion models of conventional and auxetic drug-eluting stents[J]. Journal of Medical Devices, 2007, 1(1): 47-55.

[25] KOOISTRA G W, DESHPANDE V S, WADLEY H N G. Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminium[J]. Acta Materialia, 2004, 52(14):4229-4237.

In-plane impact dynamic analysis for a sinusoidal curved honeycomb structure with negative poisson’s ratio

DENG Xiaolin， LIU Wangyu

(School of Mechanical & Automotive Engineering， South China University of Technology， Guangzhou 510640， China)

A fully parameterized sinusoidal curved honeycomb structure was studied, the software Pro/Engineer was used to build the parameterized model of the honeycomb structure. The finite element model for the honeycomb structure was established using the software ABAQUS. Its in-plane dynamic responses with different amplitudes and cell wall thicknesses under different impact velocities were studied. The results showed that the reaction forces of the honeycomb structure is directly related to its amplitudes and impact velocities; the smaller the amplitudes and the thicker the cell wall thickness, the more obvious the fluctuations of reaction forces; the higher the impact velocities，the more obvious the fluctuations of reaction forces; if the honeycomb structure has larger amplitudes, its reaction forces have a good stability under different impact velocities; the honeycomb structure fixed end’s platform stress mainly depends on the cell wall thickness, but independent on impact velocities; with increase in amplitudes, the structure’s energy absorption capacity drops; with increase in impact velocities, the structure’s energy absorption ability tends to be consistent; its slight dilatancy effect can enhance its energy absorption capacity in plane; compared with the energy absorption ability of a regular hexagonal honeycomb structure, that of a sinusoidal curved honeycomb structure is better.

negative poisson’s ratio； sinusoidal curve； honeycomb structure; in-plane impact

广东省自然科学基金(2014A030313251)；广西自然科学基金(2014JJBA60066；2016JJA110045)；广西高校中青年教师基础能力提升项目(KY2016YB437)

2015-12-28 修改稿收到日期：2016-04-21

邓小林 男，博士,1984年生

刘旺玉 女，博士，教授，博士生导师，1966年生 E-mail:mewyliu@scut.edu.cn

O343

A

10.13465/j.cnki.jvs.2017.13.016