七芯铠装电缆传输特性仿真模型研究

王鋆晟，孟文博，文晓哲，王洪超

（吉林大学仪器科学与电气工程学院，吉林 长春 130026）

七芯铠装电缆传输特性仿真模型研究

王鋆晟，孟文博，文晓哲，王洪超

（吉林大学仪器科学与电气工程学院，吉林 长春 130026）

为经济有效地获取任意长度七芯铠装电缆的传输特性，基于多导体传输线理论对七芯铠装电缆的传输特性进行建模仿真分析。首先采用有限元方法计算模型参数即电缆单位长度分布参数，将趋肤效应和钢制铠装邻近效应的影响计算在内；然后以相似变化思想解模型方程即多导体传输线方程，获得电缆近端及远端传输特性曲线；最后以长度为3km的七芯铠装电缆为例，将模型仿真结果与实测数据进行对比，证明模型的有效性。结果表明：外围缆芯的传输特性更加复杂多变且衰减剧烈；中间缆芯的传输特性衰减变化较平缓，更适合用于高速通信。

七芯铠装电缆；多导体传输线；有限元仿真；传输特性

0 引 言

在VSP测井及水力压裂过程监测等井中测试领域，对作为传输介质的七芯铠装电缆的传输特性有清晰的认识是进行高质量数据传输的前提。测试过程中所使用的七芯铠装电缆长达几千米，信号在电缆上的传输属于长线传输，受分布电阻、分布电感、分布电容等参数的影响,电缆可用带宽很窄,长期以来一直是提升井中数据传输速率和质量的瓶颈。此外,电缆的传输特性具有非线性，非线性信道对不同形式的信号所产生的影响也不尽相同，很难给出固定参数来精确计算信号传输特性[1]。

自20世纪70年代末，Clayton教授[2-4]系统地提出多导体传输线理论，并采用这种有效的近似分析方法分析了带状电缆、双绞线电缆信号传输过程的衰减、串扰问题，使得多导体传输线理论在多芯电缆传输特性的分析领域得到了广泛的应用。如Mazloom等[5]针对瑞典铁路用悬空信号电缆，进行了建模和试验研究；Spadacini等[6]借助多导体传输线理论对卫星供电线路的电磁辐射量进行预测研究；谢彦召等[7]对架空多导体传输线缆的电磁脉冲响应进行了计算，为防护设计提供参考。七芯铠装电缆相对于常用多芯电缆结构更加复杂，七根绞在一起的屏蔽电缆的外侧尚有一层厚厚的钢制铠装。受铁磁性物体临近效应的影响，电缆传输特性变化情况更加难以预测。目前国内主要采取测试方法获得七芯铠装电缆的传输特性[8]。但对千米级七芯铠装电缆而言，测试法需针对不同的通信方案和硬件连接状况分别进行测试，不仅会严重延迟研发进度，还需要大量经费支持。

为了以一种经济有效的方法获得任意长度的七芯铠装电缆的传输特性。参照上述多芯电缆传输特性分析方法，本文将七芯铠装电缆视作一种准TEM（横向电磁场，即电场和磁场分量均分布在与传播方向垂直的平面内，也即沿传播方向没有电场和磁场分量）结构，则各缆芯间的电压和流过缆芯的电流能够被唯一的定义，继而可通过建模方法获得电缆的传输特性。

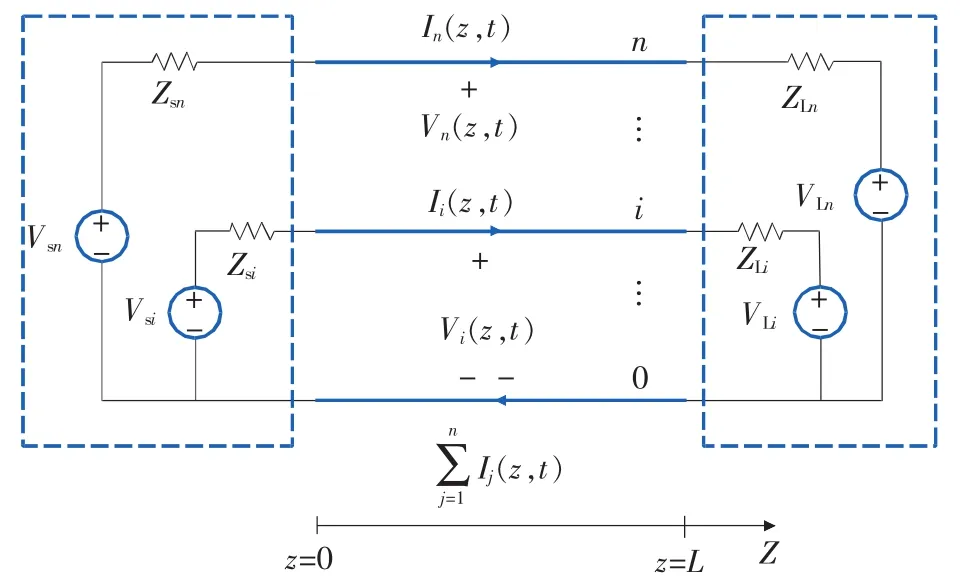
图1 多导体传输线系统

1 理论基础

本文将七芯铠装电缆视作一种准TEM结构，也是一种多导体传输线结构，因而可借助多导体传输线理论[9]建立模型分析铠装电缆的传输特性。

分析一个由n+1个导体组成的总长为L的多导体传输线结构，n+1个导体互相平行且平行于Z坐标轴（如图 1 所示）。 在近端（z=0）和远端（z=L）处的链接网络以广义戴维南模型表示，包含集中式激励源。

假设电磁场沿导体传输时是横向电磁场（TEM）结构，以0号导体作为参考导体和电流回路，传输线方程为

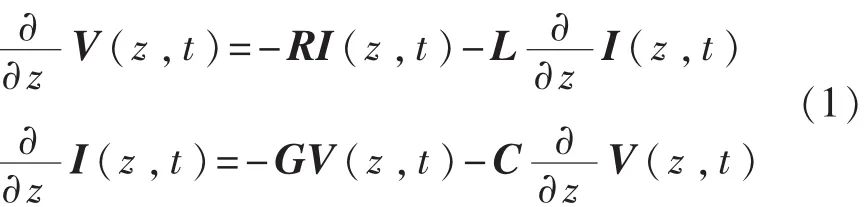
其中V和I为n×1阶向量，包含n个导体的电压[V（z，t）]i=Vi（z，t）和 n 个导体的电流[I（z，t）]i=Ii（z，t），i代表此分量处于向量中的第i行，也代表此分量是第i个导体的数据，z表征其在z轴上的坐标，t表征时间。同样其中R、L、C、G分别是单位长度电阻矩阵、单位长度电感矩阵、单位长度电容矩阵和单位长度电导矩阵。各矩阵组成元素如图2所示，单位长度参数矩阵的形式如下式：

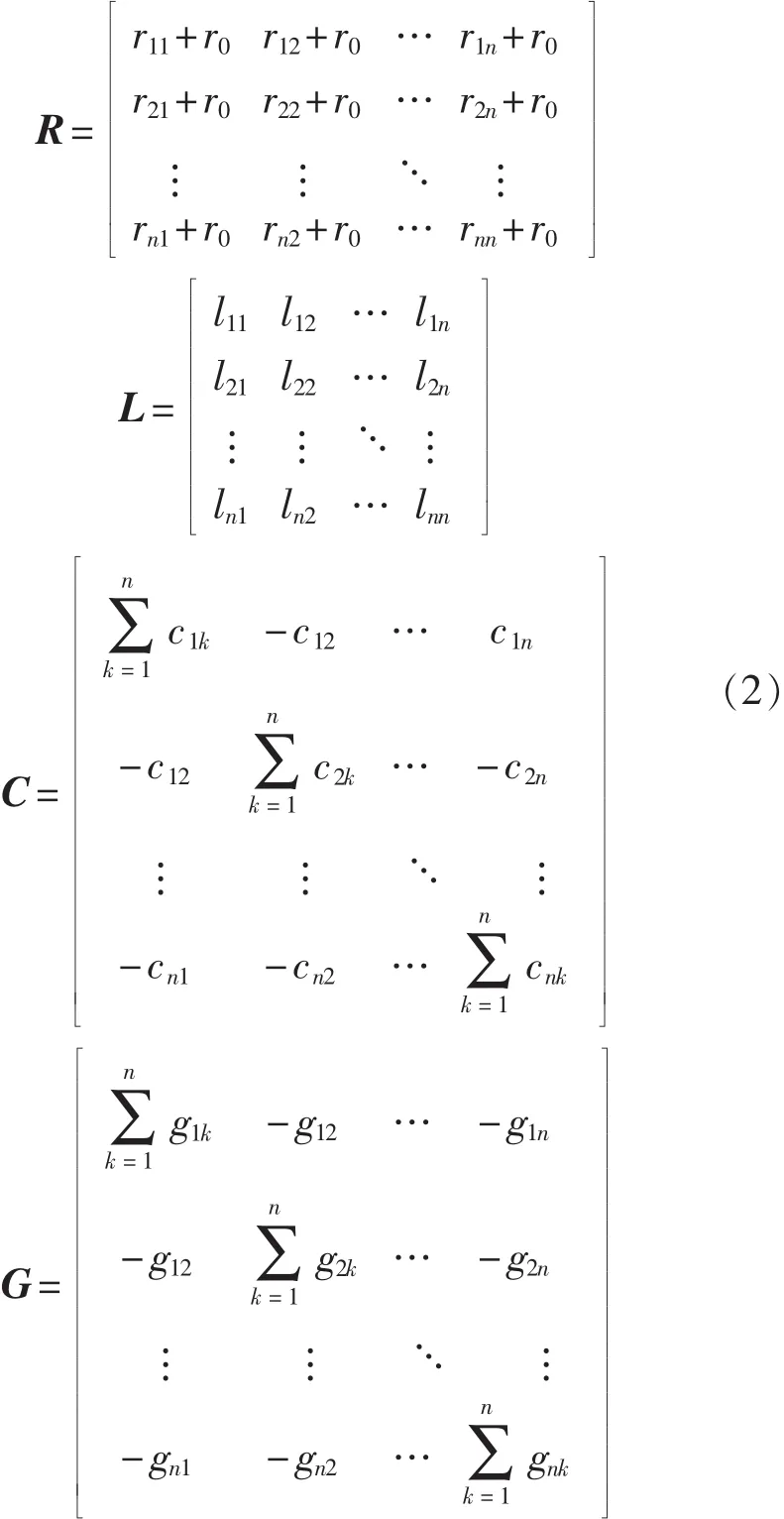
从多导体传输线理论可知获得多导体传输线的单位长度分布参数是对多导体传输线分析的前提条件，解多导体传输线方程是获得各个导体上的电压、电流分布的必要过程。因而本文将首先通过有限元法计算七芯铠装电缆的单位长度分布参数矩阵R、L、C、G（获取模型参数），然后通过矩阵转换方法解多导体传输线频域方程（解模型方程）以获得千米级电缆的传输特性。

图2 单位长度等效电路图

2 模型建立

由理论分析可知，对七芯铠装电缆的传输特性建模分析主要分为两步。

2.1 有限元法计算模型参数

一般情况下，传输线的单位长度参数多采用解析方式获得。解析方式简洁迅速，但只能解决简单结构的问题，对结构更加复杂的多导体传输线（如七芯铠装电缆）是无能为力的[10]。

本文采用有限元方法计算七芯铠装电缆的单位分布参数，不受复杂结构的限制，且能充分考虑到趋肤效应和邻近效应对单位参数的影响，获得各对应频率点下分布参数值。具体思路如下：

一个任意形状的截面图形Ω如图3所示，其中Ω1，Ω2，…，Ωn为 n 个导体（本文中即为缆芯），Ωn+1，Ωn+2，…，Ωn+m为包围着n个导体的m块介电常数不同的绝缘区域（本文中为缆芯外绝缘物质）。

又有差分形式的频域麦克斯韦方程组为

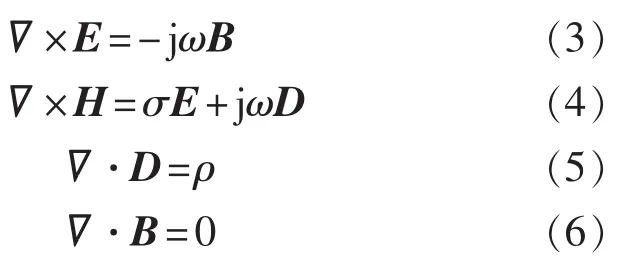
式中：σ——电导率；

E——电场强度；

B——磁通量密度；

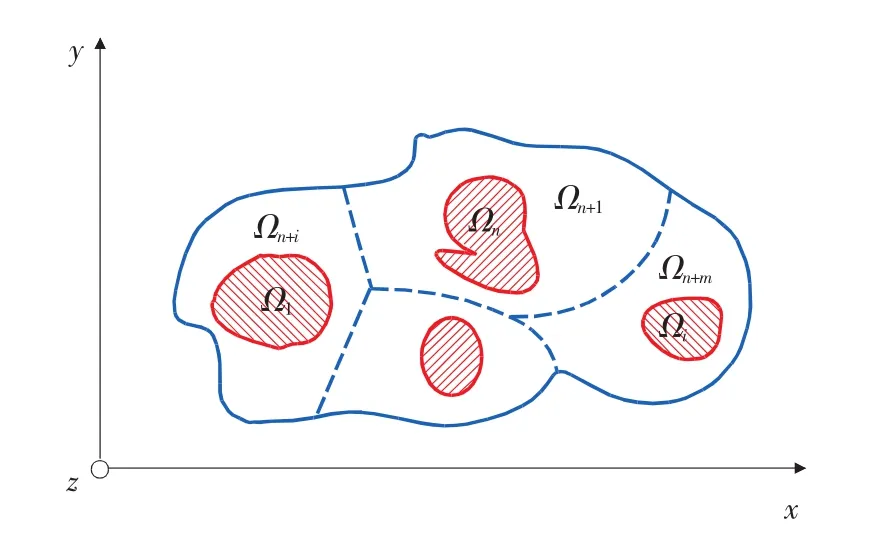
图3 截面的几何构造

H——磁场强度；

D——电通量密度；

ρ——电荷密度；

ω——角频率。

2.1.1 求解电阻、电感

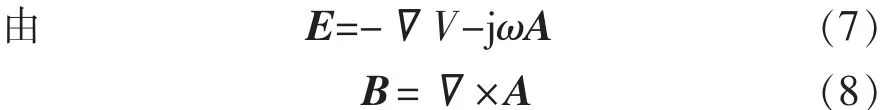
结合式（3）和式（4）可得：

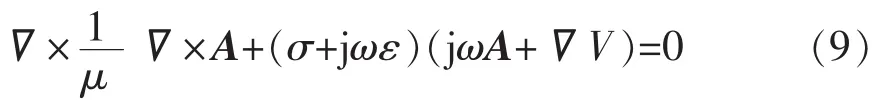
采用有限元方法结合诺埃曼边界条件n×A=0（n为截面区域Ω边界的法向量）在电缆截面区域内解方程,可解得截面区域内电流分布状况。

从能量损耗角度[11-14]计算自电阻值rii：

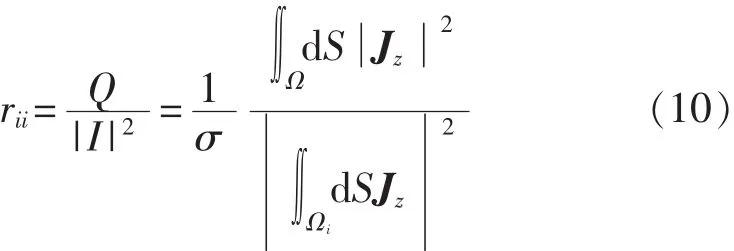
式中Jz为沿Z轴方向流过电缆横截面的电流密度矢量。

在计算出自电阻后，假设i导体中电流为Ix，j导体中电流为-Ix，则功率损耗Q与互电阻rij的关系为

自电感Lii和互电感Lij是通过计算整个区域的磁蓄能Wm获得：

假设i导体和j导体流过的电流分别是Ii和Ij，其他导体内电流为0，则：

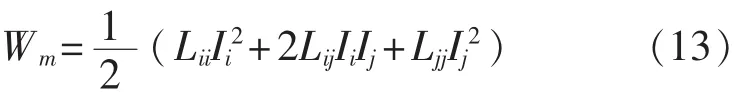
2.1.2 求解电容

自电容和互电容是通过在所有非导体区域内解给出狄利克雷边界条件的拉普拉斯方程获得电势分布后求得。

计算i导体的自电容Cii时将其表面电位设为Vi，其他导体表面和铠装表面电位均为0，则：

We为在所有非导体区域Ωm=Ωn+1∪Ωn+2∪…∪Ωn+m内的电场蓄能：

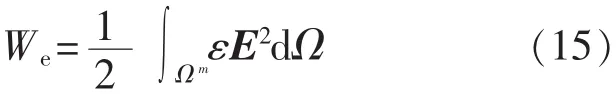
互电容Cij则是假设相应的i导体和j导体的表面电位分别为Vi和Vj。

2.1.3 求解电导

电导表征导体周围介质的导电性能，因铠装电缆采用的绝缘介质，电导值很小趋近于0，本文中假设其为0。

2.2 频域方法解模型方程

按上述方法求得模型参数后，获得传输特性的过程转化为求解模型方程（多导体传输线方程）的过程。本文通过相似变换的方法求解多导体传输线方程[15]。

假定随时间变化的传输线的激励源是正弦波并已处于稳态。因此，传输线上的电压和电流也是与激励源同频率的正弦波。则多导体传输线方程的频域形式为

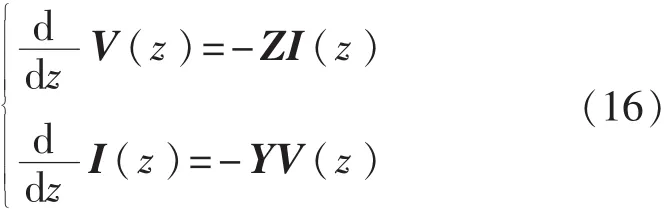
其中n×n单位长度阻抗矩阵 Z=R+jωL，导纳矩阵Y=G+jωC。

假设传输线是均匀的，即传输线横截面的尺度和传输线周围介质的特性沿传输线均是不变的（与Z无关）。将式（16）转化为二阶常微分方程

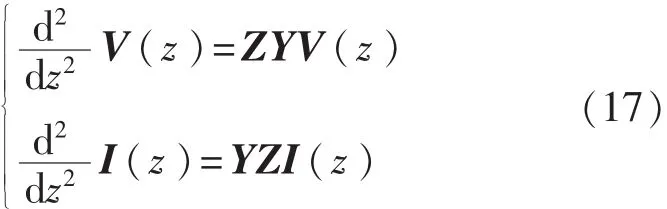
上式方程是互相耦合的。因为ZY和YZ是满秩矩阵，即每一组的电压 Vi（z）和电流 Ii（z）影响着其他所有组的电压和电流。求解方法的基本思想是采用相似变换对方程解耦。

进行模量变换：

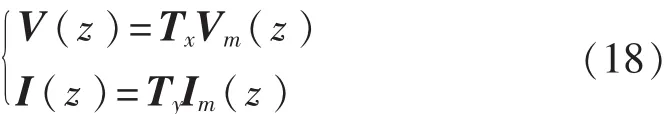
其中n×n非奇异复矩阵Tx和Ty定义为传输线上实际的相量电压V和I与模电压Vm和Im间的变量变换，则式（17）可变为

这里γ2是一个n×n对角矩阵：

若能找到变换矩阵Tx和Ty，则式（19）被成功解耦。

因为Z和Y均为对称阵，则ZY的转置即是YZ，有相同的特征值，因此只需找到Tx和Ty中的一个，就能解耦方程。方程（19）解耦后，参照双导体传输线计算思路，可得到解为

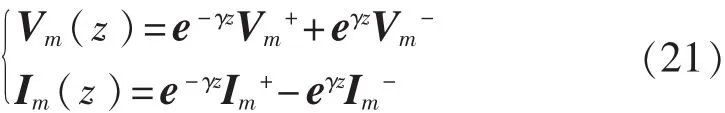
其中，指数矩阵定义为

Vm和Im是n×1待定常数向量，它们与前向、反向横行波有关，即：

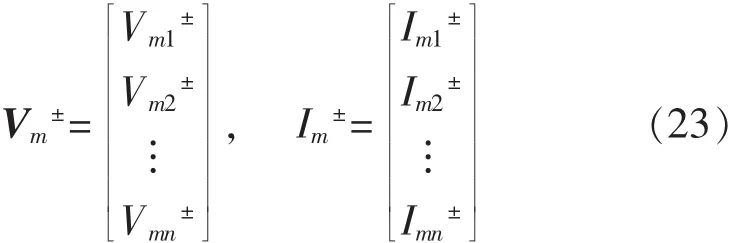
利用式（18），可以将求得的模电压和模电流通过变换获得传输线上实际的电压和电流：

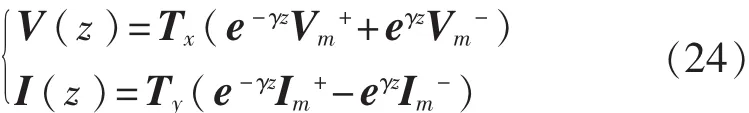
也可转化为仅用Im表示，即：

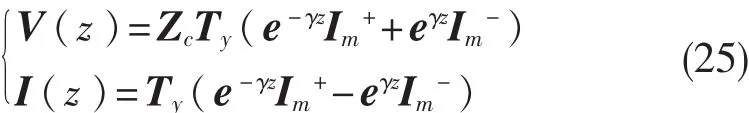
其中Im+、Im-在方程解偶后结合如图1所示的终端条件，由下式求得：

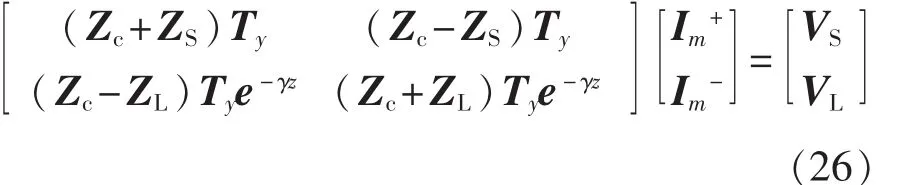
其中特征阻抗矩阵 Zc=ZTyγ-1Ty-1。 电压矩阵 VS、VL表征图1中近端及远端的电压量，阻抗矩阵ZS、ZL表征图1中近端及远端的端接阻抗。

通过上述过程求得长度为z的七芯铠装电缆上的电压、电流值，即可获得其传输特性。

3 模型验证及实例应用

按上述建模方法对一长度为3 km的七芯铠装电缆的传输特性进行建模仿真，首先使用有限元软件计算七芯铠装电缆的单位长度分布参数。

使用三角形有限元对七芯铠装电缆的截面进行剖分，在结构尺寸越加精细的部分进行更加精细的划分，以满足计算精度要求（见图4）。图中黑色部分即为结构交界处及精细结构被进行精细剖分的结果。各部分材质属性设置如表1所示，缆芯的材质是铜，铠装的材质是钢。

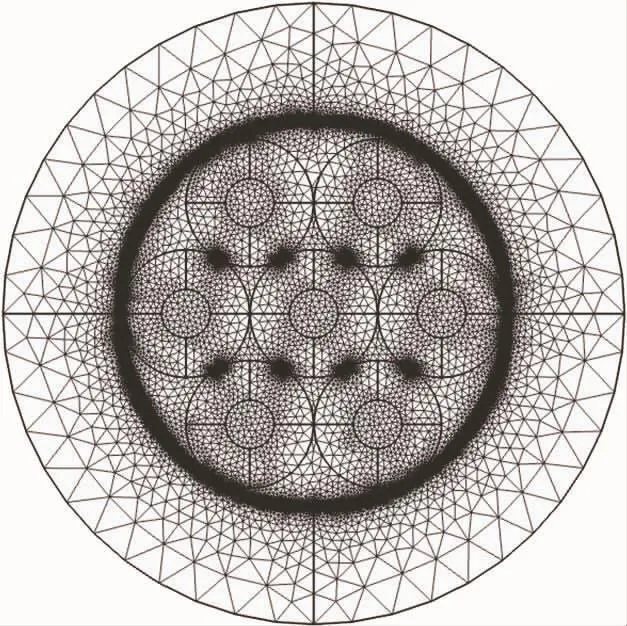
图4 电缆截面剖分效果图

表1 电缆仿真材质属性

如上文建模方法中所述对截面区域内的电流密度和电势分布进行了分析（如图5、图6所示），可看到电流密度分布和电势分布受趋肤效应和邻近效应影响明显，即铠装电缆的单位长度分布参数受频率影响。通过有限元方法计算电缆单位长度分布参数即可将邻近效应和趋肤效应的影响纳入计算范围，得到与实际状况相符的结果。

在使用有限元法获得电缆单位长度分布参数后，按2.2中所述方法使用Fortran语言编写程序解模型方程，如图1所示，在电缆末端加50Ω匹配电阻，分别以中间芯和外围芯进行信号传输仿真，获得电缆近端和远端传输特性。

对一长度为3 km缠绕在电缆盘上的七芯铠装电缆的近端及远端传输特性进行测试，在近端传输信号的缆芯处通过一内阻为50 Ω的信号源输入幅值为5V的正弦激励，其余缆芯通过50Ω的匹配电阻接地，电缆远端同仿真模型一样接以50Ω匹配电阻，逐个频率点进行测试获得测试结果。测试结果与仿真数据对比，如图7～图9所示。

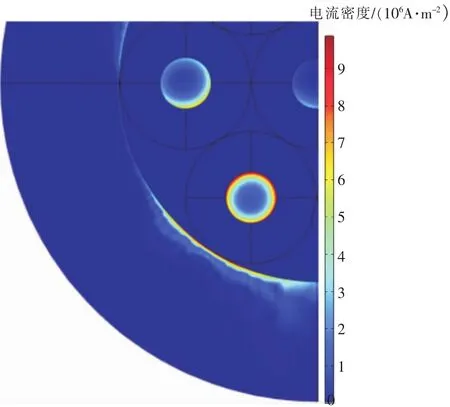
图5 相邻缆芯分别通以1A，-1A（300kHz）电流时电流密度分布

可以看出电缆近端的仿真结果可以与实测数据很好的吻合，随着频率的增大，衰减也在逐渐增大，在100kHz附近增益约为-6dB。

经过3km的传输后，外围缆芯远端的仿真结果也能较好地与实测数据吻合。但可看出幅度增益波动剧烈，在100kHz附近波动可达5dB，因而外围缆芯不适合用于高速传输方案，会产生较高的误码率。

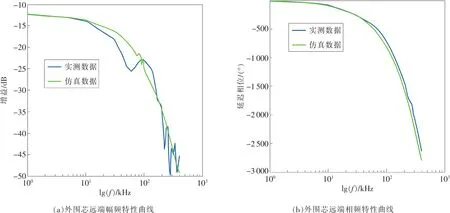
图8 3km电缆外围芯远端传输特性

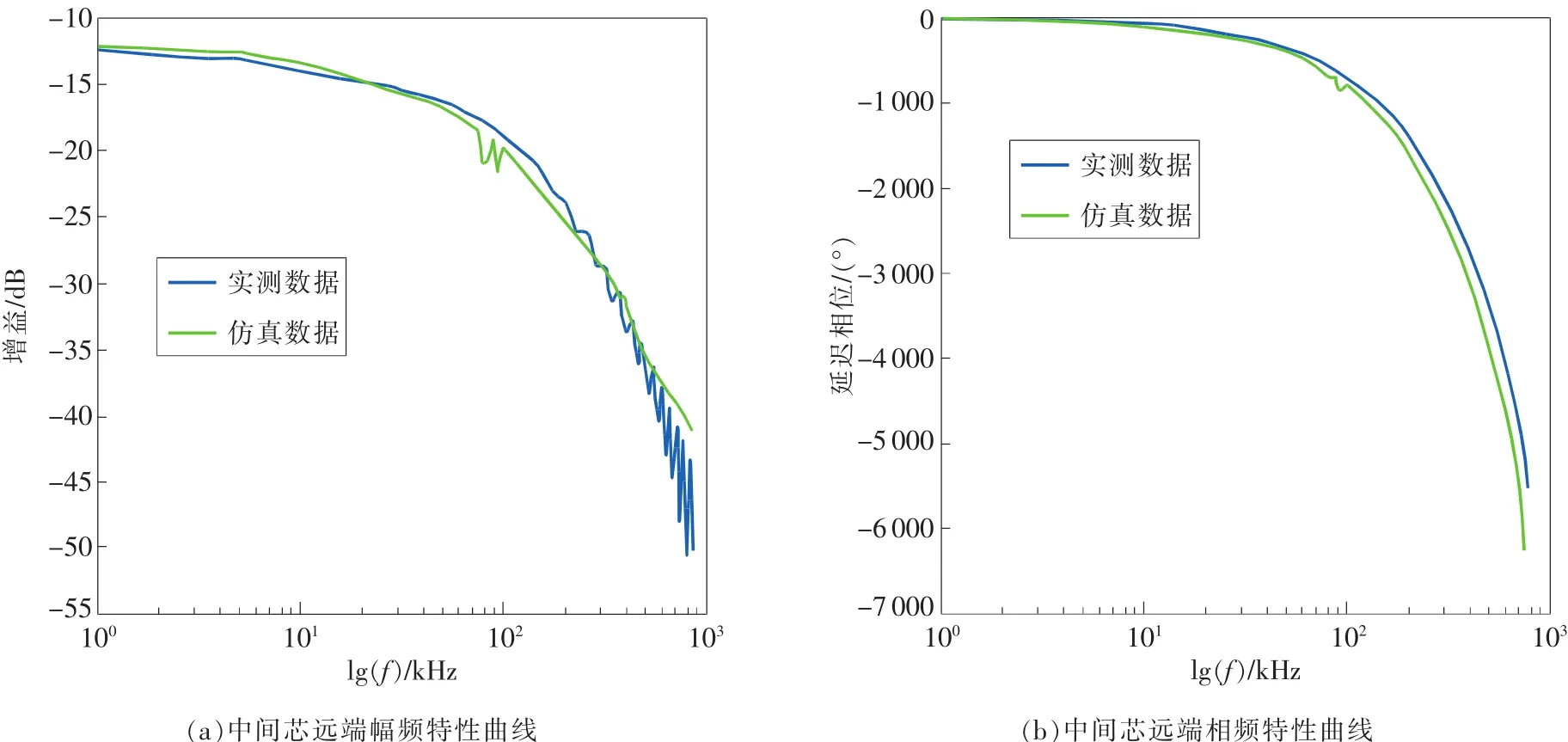
图9 3km电缆中间芯远端传输特性

从图中可看出，中间缆芯远端的仿真结果能更好地与测试结果吻合，且通过与图8对比可看出，中间缆芯衰减更小，幅度曲线更平滑，可以很好地解释七芯铠装电缆应用中的经验性结论：外围缆芯的传输特性更加复杂多变，且衰减剧烈；比较而言，中间缆芯更适合用于高速通信。

综上所述，通过文中所用仿真模型可以简单有效地获得任意长度七芯铠装电缆的传输特性，且结果中的误差是在假设整根七芯铠装电缆是均匀的，即电缆任意一处横截面的尺寸和周围介质的特性沿电缆轴向均不变的前提下产生的，这与实际情况有一定偏差。若对精度有更高要求，可将长距离铠装电缆进行分段，每一段的截面尺寸和周围介质属性根据实际情况分别设置，上一段的输出作为下一段的输入进行更加精细的处理，即可根据需求得到更高的精度。

4 结束语

本文基于多导体传输线理论对七芯铠装电缆的传输特性进行了建模，采用有限元法计算模型参数，通过矩阵转换方法解模型方程，获得了电缆近端与远端的传输特性。并以长度为3km的电缆为例，将模型仿真结果与实测结果进行了对比，证明了仿真模型的有效性。实际应用中铠装电缆沿轴向方向截面特性受多因素影响，并非均匀不变的。为进一步提高精度可将电缆截面特性沿轴向变化情况作为模型参数之一纳入考虑范围，进行分段计算，但精度的提升是以计算量的增加为代价的。

[1]张菊茜，卢涛，李群，等.一种基于OFDM技术的900 Kbit/s测井数据传输系统[J].测井技术，2009，33（1）：84-88.

[2]CLAYTON R P.Solution of the transmission line equations for lossy conductorsand imperfect earth[J].Proceedings of the Institution of Electrical Engineers，1975，122（2）：177-182.

[3]CLAYTON R P.A brief history of work in transmission lines for EMC applications[J].IEEE Transactions on Electromagnetic Compatibility，2007，49（2）：237-252.

[4]CLAYTON R P.A serious problem in using the jarvis model for the prediction of crosstalk[J].IEEE Electromagnetic Compatibility Magazine，2012，1（3）：46-55.

[5]MAZLOOM Z， THEETHAYI N， THOTTAPPLLIL R.Indirect lightning-induced voltages along a railway catenary-track multiconductor transmission-line system with lumped components[J].IEEE Transactions on Electromagnetic Compatibility，2011，53（2）：537-539.

[6]SPADACINI G， GRASSI F， BELLAN D， et al.Prediction of conducted emissions in satellite power buses[J].International Journal of Aerospace Engineering，2015，41（3）：439-448.

[7]谢彦召，王赞基，王群书，等.架空多导体传输线缆的电磁脉冲响应计算[J].清华大学学报（自然科学版），2006，46（4）：449-452.

[8]杨小锋.测井电缆特性测试技术研究[D].大庆：东北石油大学，2014.

[9]ANTONINIG，ORLANDI A，PIGNARIS A.Review of Clayton R.PaulStudies on Multiconductor Transmission Lines[J].IEEE Transactions on Electromagnetic Compatibility，2013，55（4）：639-646.

[10]DARCHERIF A， RAIZER A,SAKELLARIS J， et al.On the use of the surface impedance concept in shielded and multiconductor cable characterization by the finite element method[J].IEEE Transactions on Magnetics，1992，28（2）：1446-1449.

[11]BONYADI-RAM S， KORDIB， BRIDGES G E.A Full-space conformal mapping for the calculation of series impedance of overhead transmission lines and underground cables[J].Electric Power Systems Research，2012（91）：95-103.

[12]杜学峰.长电缆传输研究[D].合肥：中国科学技术大学，2006.

[13]DEMEESTER T， GINSTE D V， DANIËL D Z.Accurate study of the electromagnetic and circuit behavior of finite conducting wedges and interconnects with arbitrary cross-sections[C]∥IEEE 19th Conference on Electrical Performance of Electronic Packaging and Systems.Washington DC：IEEE Computer Society，2011：133-136.

[14]RASOULPOOR M，MIRZAIE M，MIRIMANI S M.Losses distribution in sheathed power cables under non-sinu soidal currents using numerical method[J].Computer Aplications in Engineering Education，2016，24（5）:692-705.

[15]CLAYTON R P.多导体传输线分析[M].杨晓宪，郑涛，译.2版.北京：中国电力出版社，2013:176-191.

（编辑：李妮）

Simulation research on seven-core armored cable’s transmission characteristics

WANG Junsheng，MENG Wenbo，WEN Xiaozhe，WANG Hongchao
（College of Instrumentation ＆ Electrical Engineering，Jilin University，Changchun 130026，China）

In order to obtain the transmission characteristics of seven-core armored cable of arbitrary length in a cost-effective manner，based on the theory of multiconductor transmission lines，the transmission characteristics of seven-core armored cable were simulated and analyzed.Firstly，the finite elementmethod wasused to calculate the cable unitlength distribution parameters，and the effect of the skin effect and proximity effect caused by steel armor were calculated.Then，the transmission equation of the multiconductor was solved by the similarity transformation idea.Finally，the simulation results of seven-core armored cable with length of 3km were compared with the measured data，which proved the effectiveness of the model.The results show that the transmission characteristics of the outer cable core are more complicated and decay drastically.The transmission characteristics of the inter cable core change more slowly and more suitable for high-speed transmission.

seven-core armored cable；multiconductor transmission line；finite element simulation；transmission characteristics

A

1674-5124（2017）04-0118-07

10.11857/j.issn.1674-5124.2017.04.025

2016-09-03；

2016-10-20

国家自然科学基金项目（41074074）

王鋆晟（1989-），男，河南平顶山市人，硕士研究生，专业方向为井下通信技术。