基于禁忌搜索的战略投送枢纽选址研究

毕海玲，张旭涛，傅 钰

(军事交通学院 装备保障系，天津 300161)



● 基础科学与技术 Basic Science & Technology

基于禁忌搜索的战略投送枢纽选址研究

毕海玲，张旭涛，傅 钰

(军事交通学院 装备保障系，天津 300161)

为解决战略投送枢纽的选址与分配问题，将战略投送网络选址问题抽象为轴辐式多式联运问题，建立带时间约束的0-1整数规划模型。针对模型的复杂性，设计一种基于特定最短路算法和禁忌搜索的启发式算法，运用仿真算例验证算法的收敛性和有效性。研究表明，该算法能有效对模型求解，可为国防交通建设规划提供决策参考。

战略投送；枢纽选址；整数规划；禁忌搜索；最短路算法

战略投送是指综合运用国防战略交通运输力量，采用多种输送方式，将战略纵深军事力量及装备投送到遂行任务的地区，以在特定的区域内快速聚焦军事力量，形成有利态势，争取行动主动权的军事行动[1]。战略投送在实施过程中，一般首先将人员和物资通过摩托化机动的方式在国防交通枢纽处集结，然后利用国防交通干线通过多种运输方式集中运输到离任务点最近的交通枢纽，最后根据任务需求对人员和物资进行分散运输(摩托化机动)到达配置地域。战略投送枢纽的选址与分配问题是国防交通规划与调度中面临的一个重要问题。现有的战略投送研究一般属于定性研究[2-3]，传统枢纽选址问题研究大多只针对单一运输网络建立总成本最小规划模型[4]，现有多式联运研究多集中在联运路线的选择方面[5]，枢纽选址问题的研究较少，且一般只考虑优化网络成本。多式联运中节点之间存在多种运输方式，节点之间同一方向含有多重边，使得多式联运枢纽选址问题变得更为复杂。现有研究[6-7]在求解分配子问题时一般是将其转化为无容量约束的指派问题，由于在优化过程中需要反复多次求解子问题，运算量很大，算法效率不高。另外，战略投送对运输时间有比较高的要求，在枢纽选址建模时必须考虑时间约束，模型求解较为困难。

本文将战略投送常规枢纽选址问题抽象为带时间约束的多式联运轴辐式网络枢纽选址问题，建立无容量约束多分配0-1整数规划模型。针对模型参数变量多、组合优化难以定量求解的特点，将问题分解为枢纽选址问题和交通流分配两个子问题。其中选址问题采用禁忌搜索算法，而对于分配问题，通过节点间的路权比较以及是否满足时间约束，将多边网络简化为单边网络，采用有限迭代的Floyd最短路算法整体求解，使整个算法的计算量大大减少。

1 问题描述及假设

战略投送中，采用多种运输方式对人员和物资进行输送，其过程属于多式联运[8]。其中：摩托化机动看作多式联运中的公路运输，干线运输过程采用铁路运输或公路运输；战略投送网络可抽象为轴辐式网络结构[9]，人员和物资的出发点以及最终到达的各配置地域看作网络中的非枢纽节点，集结点和配置中心可看作网络中的枢纽节点。本文研究基于以下假设：①枢纽网络为完全网络；②枢纽间采用干线运输时，由于规模效应，运输成本和成本存在一个折扣系数；③一个非枢纽节点可以与多个枢纽节点相连，非枢纽节点间不能直接相连；④任意起讫点的人员物资运输最多经过两个枢纽进行转运；⑤在采用干线运输时需要转运，转运成本和时间计算在枢纽对之间；⑥枢纽和干线运输无容量限制。

2 模型构建

2.1 模型参数

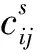
2.2 决策变量

2.3 整数规划模型

基于以上模型假设和模型参数设置，建立战略投送枢纽选址整数规划模型：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

∀i,j,k,m∈N,s∈S

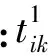
3 基于特定Floyd最短路的禁忌搜索算法

枢纽选址分配属于组合优化问题，已经被证明为NP难问题[10]，采用启发式算法求解是一种普遍的做法。在常见的启发式算法中，禁忌搜索[11]能模拟人类的思考过程，利用短期和长期禁忌表，避免迂回搜索并能跳出局部最优，对解决此类复杂的组合优化问题非常有效。在搜索过程中，涉及反复多次求解给定枢纽集时，如何确定非枢纽点与枢纽点之间的分配关系以及起讫点间的运输路线与运输方式的问题，本文设计了一种特定Floyd最短路算法整体求解。

3.1 特定Floyd最短路算法

Floyd最短路算法是用于整体求解给定权重简单图最短路的最常用方法。由于战略投送运输网络中节点间同一方向存在两种运输方式，属于复杂网络，需要对网络进行特定简化。另外，模型中含有时间约束，当以成本为权重的最短路满足时间约束时，以该最短路作为问题的满意可行解。当不满足时间约束时，选择以时间为权重求解最短路问题，作为问题的满意可行解。如以时间为权重求解得最短路仍不满足时间约束，则该枢纽选择方案不可行。

设p个枢纽构成的枢纽集为H={h1,h2,…,hp}，构造图G=(N,E)，其中N={1,2,…,n}，eij∈E，取i→j权重最小的边，于是含有多重边的多式联运网络可以简化成不含多重边的简单图。令网络的权矩阵为D=(dij)n×n，当以成本最小化求解最短路时，有

(8)

当以时间最小化求解最短路时，有

(9)

令网络的路由矩阵为R=(rij)n×n，其中rij=j为节点i到节点j最短路所经过的第一个点的下标。Floyd最短路算法的基本步骤：

(1)输入权矩阵D(0)=D，R(0)=R。

传统Floyd算法的复杂度为O(n3)，由于模型假设非枢纽节点只能与枢纽节点连接，如果将枢纽节点与非枢纽节点区分，上述迭代过程仅需要迭代p次即可。由于战略投送任意节点间的交通流为对称交通流，i→j与j→i是同一条路线，该模型中分配问题算法的实际复杂度为O(pn2/2)。

3.2 禁忌搜索算法设计

(1)解及邻域的构造。随机产生一组节点作为初始枢纽集，采用将一个非枢纽点与枢纽点对换的方法来构造邻域空间。

(2)评价函数。采用式(1)作为解的评价函数，搜索过程根据评价函数优劣进行移动。

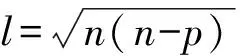
(4)禁忌频率。将每次运行算法时节点被禁忌的频率记录下来并累加作为一种长期记忆，在产生下一次运行算法的初始解时避开那些禁忌频率高的节点，以使搜索向未搜索过的解空间区域进行。

(5)特赦准则。若某个禁忌候选解优于当前最好解，则解禁此候选解并将其作为当前解和最优解；若候选解均被禁忌，且不存在优于最优解的候选解, 则对候选解中最佳的候选解进行解禁作为当前解。

3.3 算法基本步骤

步骤1 设置禁忌表为空，设置算法的最大运行次数MaxRun，每次运行最大迭代次数MaxIteration和最优解连续不变的迭代次数MaxCount，设置节点禁忌频率矩阵对应频率NodeFrequency=0。

步骤2 产生初始解StartingSolution，令当前解CurrentSolution=StartingSolution，最优解BestSolution=CurrentSolution。

步骤3 产生当前解的邻域，求解邻域内所有枢纽集的最短路问题，若存在可行解，对可行解根据评价函数进行排序，作为待选解，转步骤4；若不存在可行解，选择评价函数最小的枢纽集作为当前解，转步骤7。

步骤4 最好的待选解是否优于最优解，若是则转步骤7，若否则转步骤5。

步骤5 所有解是否都被禁忌，若是选择最好的候选解作为当前解，若否将非禁忌的最好候选解作为当前解，转步骤7。

步骤6 将该解作为当前解，并更新最优解，更新禁忌表和禁忌频率，迭代次数Iteration+1，转步骤8。

步骤7 更新当前解，更新禁忌表和禁忌频率，迭代次数Iteration+1，最优解连续不变的迭代次数Count+1。

步骤8 若迭代次数和最优解连续不变的迭代次数均未达到限制，则继续迭代；若已达到限制，运行次数run+1，并转步骤9。

步骤9 将禁忌频率高的节点排除在外，产生新的初始可行解，转步骤2。

步骤10 运行次数达到最大限制，结束算法，输出结果。

4 算例

本文算例数据采用仿真方法产生，产生数据时满足一定规则，以符合实际情况。设置参数值时参考了相关多式联运枢纽选址文献[6-7]中的数值与方法。

4.1 数据产生方法

以15个战略投送节点为例介绍数据产生方法，节点间横纵坐标从[0，1 000]中抽样产生(见表1)。

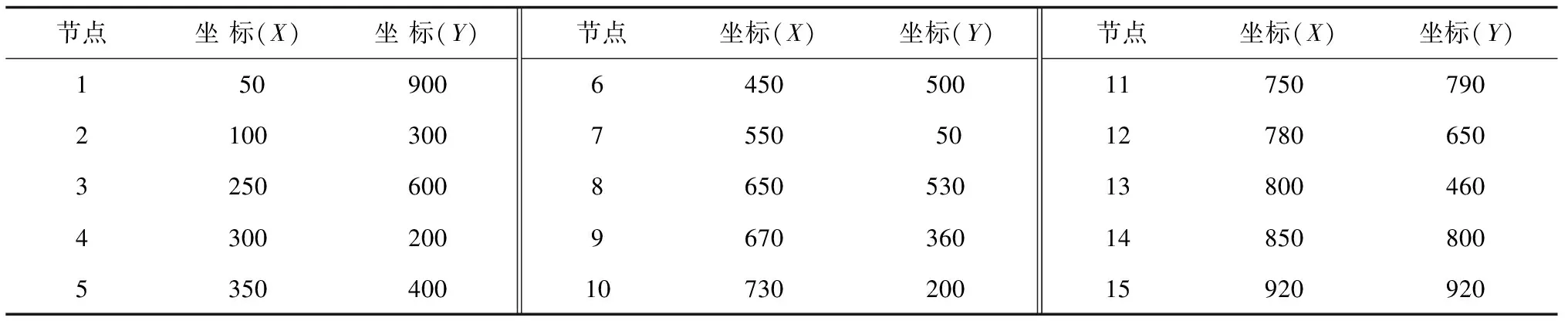
表1 网络节点编号及坐标

4.2 算法收敛性与有效性检验

对上述15节点投送网络算例进行求解，禁忌搜索算法中的禁忌长度设为7，禁忌频率设为10。设共建5个枢纽，当初始枢纽集为[2，6，12，14，15]时，记录迭代过程中当前解目标函数的变化情况并绘图(如图1所示)。由图1可知，在迭代初期的搜索过程中，目标函数迅速收敛，然后在第11次时，目标函数有所上升，这是由于禁忌搜索算法允许接受劣解，并不总是选择当前最优解作为当前解进行搜索，从而具有跳出局部最优解，在新的区域进行搜索的能力。最终，搜索过程在迭代30次后趋于收敛。因此，算法设计每次运行最大迭代次数为50次，算法重复运行15次后最优解保持不变，故设置算法的最大运行次数为20次。

为检验算法有效性，利用上述产生仿真数据的方法，分别产生节点数量为10、15、20、25、30、40、50，枢纽数量为3、5、7、9、11、13、15的投送网络数据，采用本文提出的算法求解，并与用Complex 12.0软件和Meng等[12]提出的混合遗传算法求解的结果做对比(见表2)。采用当前主流规划软件Complex求解时，求解时间随着问题规模的增大而快速增加，当投送网络节点超过30个时，Complex不能在合理的时间得到最优解，采用启发式算法则能显著改善问题的求解时间。本文提出的基于Floyd的禁忌搜索算法的求解速度要高于Meng等[12]提出的混合遗传算法，这是由于模型求解属于组合优化问题，禁忌搜索利用禁忌表避免了迂回搜索，使得寻优过程更加高效。

4.3 算例结果与分析

以15节点投送网络算例结果进行讨论，最优枢纽集为[1，5，8，10，14]，对应目标函数值为2.258 1×107元。最优枢纽集的路由矩阵见表3。从表3中不但可以得到非枢纽节点与枢纽节点间的分配关系，如非枢纽节点2全部分配给枢纽节点5，非枢纽节点9点主要分配给枢纽节点8，还可以分配给枢纽节点10；而且还可以得到任意点对间的路线，如节点3到节点9的路线为3→5→8→9，节点1到节点7的路线为1→8→10→7。枢纽间的运输方式选择可以观察最优枢纽集下的路网权矩阵，通过式(8)和式(9)反推得到，在此不再赘述。

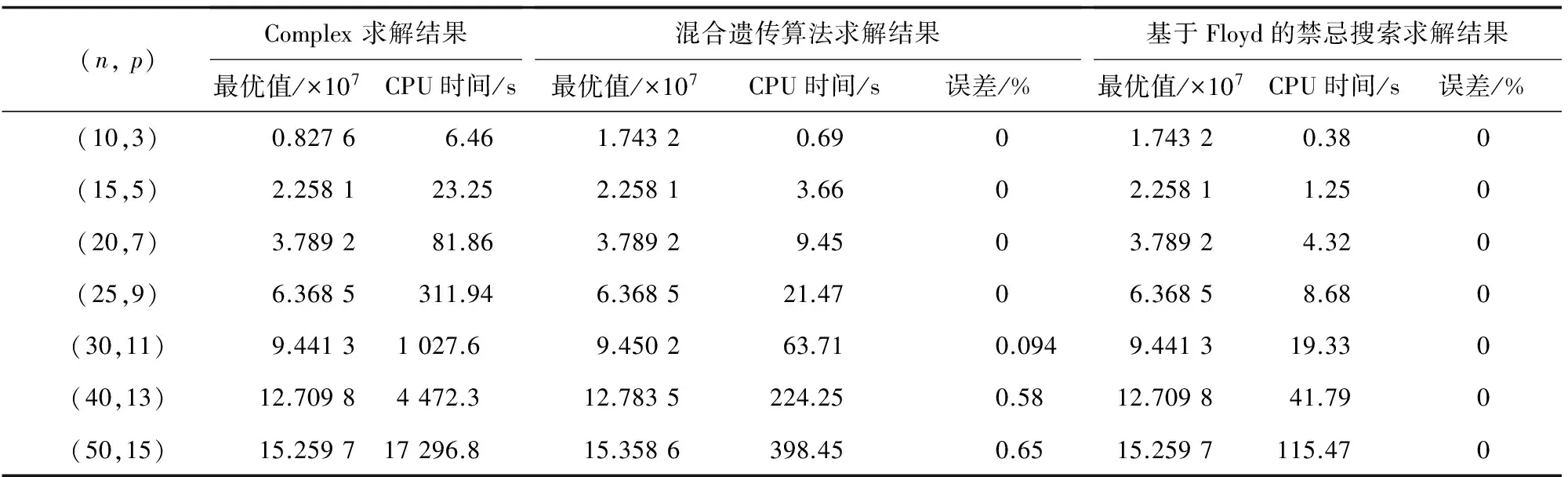
表2 基于Floyd的禁忌搜索算法与其他方法性能对比

表3 最优枢纽集下的路由矩阵

表3(续)

采用Floyd最短路算法可以得到枢纽与非枢纽间的分配关系(如图2所示)。图2中同心的双圆表示在该节点处建立枢纽，粗实线代表干线运输，细实线表示普通公路运输。观察图2可以发现，节点1在地图中属于孤点，但却在该点建立了枢纽，且只有节点3的部分运输分配到枢纽1。这是由于节点1和各个节点间均有流量，而且距离较远，如果不建为枢纽而采用通过其他枢纽中转时，由于节点间的距离满足三角不等式，势必会引起总成本的增加。

5 结 语

本文设计的算法能有效对模型求解，其结果能为国防交通建设规划提供决策参考。考虑到投送成本和时间都与投送距离成正比关系，二者具有高度的正相关性，故本文在对枢纽选址问题进行建模时是以成本作为目标函数，将时间因素放在模型约束里来考虑。战略投送由于其军事特性，时间和成本同等重要，有时甚至要优先考虑，未来研究可以将时间作为目标函数，或者将时间、成本、运量等因素综合考虑。本文研究仅考虑了公、铁联运，该模型可以扩展到公、铁、水、空多种运输方式。

[1] 管井标, 周赤非, 许瑞明, 等. 战略投送能力评估方法研究[J]. 军事运筹与系统工程, 2011, 25(2): 76-80.

[2] 张国全, 陈兆仁, 王春颖, 等. 建制部队战略投送需求基本内涵与主要特征分析[J]. 军事交通学院学报, 2013, 15(6): 1-5.

[3] 海军. 部队战略投送模式研究现状[J]. 国防交通工程与技术, 2013, 11(4): 1-5.

[4] FARAHANI R Z, HEKMATFAR M, ARABANI A B, et al. Hub location problems: A review of models, classification, solution techniques, and applications[J]. Computers & Industrial Engineering, 2013, 64(4): 1096-1109.

[5] STEADIESEIFI M, DELLAERT N P, NUIJTEN W, et al. Multimodal freight transportation planning: A literature review[J]. European Journal of Operational Research, 2014, 233(1): 1-15.

[6] ISHFAQ R, SOX C R. Hub location-allocation in intermodal logistic networks[J]. European Journal of Operational Research, 2011, 210(2): 213-230.

[7] ALUMUR S A, KARA B Y, KARASAN O E. Multimodal hub location and hub network design[J]. Omega, 2012, 40(6): 927-939.

[8] 毕海玲，张旭涛，傅钰. 联合投送背景下运输网络弹性研究[J]. 军事交通学院学报, 2015, 17(8): 83-86.

[9] BI H L, KANG K, ZHANG X T. A biobjective and trilevel programming model for hub location problem in design of a resilient power projection network[J]. Mathematical Problems in Engineering, 2016, 2016: 1-9.

[10] O'kelly M E. A quadratic integer program for the location of interacting hub facilities[J]. European Journal of Operational Research, 1987, 32(3): 393-404.

[11] Martins de Sá E, Contreras I, Cordeau J F. Exact and heuristic algorithms for the design of hub networks with multiple lines[J]. European Journal of Operational Research, 2015, 246(1): 186-198.

[12] MENG Q, WANG X. Intermodal hub-and-spoke network design: incorporating multiple stakeholders and multi-type containers[J]. Transportation Research Part B Methodological, 2011, 45(4): 724-742.

(编辑：史海英)

Hub Location in Strategic Projection Based on Tabu Search

BI Hailing, ZHANG Xutao, FU Yu

(Equipment Support Department, Military Transportation University, Tianjin 300161, China)

To solve the problems of hub location and allocation in strategic projection, the paper firstly abstracts the problem of network location into radiant multimodal transport, and establishes 0-1 integer programming model with time restraint.Then, it designs a heuristic algorithm based on specific shortest path algorithm and Tabu search according to the complexity of the model, and verifies the convergence and validity of the algorithm through simulation example. The research shows that this algorithm can solve the model and provide decision-making reference for planning national defense transportation construction.

strategic projection; hub location; integer programming; Tabu search; shortest path algorithm

2016-11-13；

2017-03-23．

毕海玲(1979—)，女，博士研究生，讲师.

10.16807/j.cnki.12-1372/e.2017.06.019

F560

A

1674-2192(2017)06- 0081- 06