循环平稳在滚动轴承故障诊断中的应用

汪治安，夏均忠，但佳壁，于明奇，吕麒鹏

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161)



● 车辆工程 Vehicle Engineering

循环平稳在滚动轴承故障诊断中的应用

汪治安1，夏均忠2，但佳壁2，于明奇1，吕麒鹏1

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通学院 军用车辆系，天津 300161)

为探索循环平稳在滚动轴承故障诊断中的应用原理及研究现状，论述循环平稳对滚动轴承故障振动信号的解调原理；研究二阶循环平稳和高阶循环平稳在滚动轴承故障诊断中的应用，并分析其优点和不足；阐述变转速工况下滚动轴承故障诊断方法——角度/时间循环平稳。结果表明，高阶循环平稳和角度/时间循环平稳的应用是滚动轴承故障诊断的研究方向之一。

滚动轴承；故障诊断；循环平稳；高阶循环平稳；角度/时间循环平稳

滚动轴承在各种机械中的旋转部件工作，其振动信号具有周期性变化的特点，当出现点蚀故障时，其振动信号是循环平稳随机信号[1]，可以利用循环平稳理论对滚动轴承进行故障诊断。

循环平稳信号是指其统计特征参数随时间按周期或多周期规律变化的一类非平稳信号[2]。循环平稳信号不同于一般的非平稳信号，它本身具有非平稳性，但同时又表现出周期性，兼具了平稳性和非平稳性的特点，表现为周期性非平稳。

相比于其他现代信号处理方法，循环平稳分析具有自己独特的优势。

(1)循环平稳信号具有周期平稳性，克服了非平稳信号无法用时间平均代替集合平均的缺陷，简化了分析难度，有利于工程应用。

(2)具有完整的理论体系，将循环平稳随机过程的研究建立在循环统计量的基础上，使得理论和实践上都有充足的依据。

利用循环平稳表征故障特征的方式主要有3种：①利用二阶循环平稳的α-f平面的离散循环频率α来表示故障特征频率；②将循环统计量转换到时频域中表示故障特征；③利用高阶循环平稳的双谱来表示故障特征。为了实现变转速工况下轴承故障诊断，循环平稳理论也从稳态假设条件下的循环平稳，扩展到非稳态假设条件下的广义准循环平稳理论[3]。

1 滚动轴承故障振动信号的循环平稳分析

McFadden等[4]首先提出了滚动轴承点蚀、疲劳剥落等单一局部故障的理论模型；此后，Antoni等[5-6]对该模型进行了改进，引入滚道和滚动体之间的微小随机滑动，得到的模型更加符合轴承的实际运行状况。

将s(t)视为滚动轴承点蚀故障的一次脉冲，其所对应的幅值为Ai，T为脉冲产生的周期，n(t)为零均值的加性噪声，考虑滚动体与滚道之间的微小滑动τ(i)，则滚动轴承故障振动信号模型可描述为

x(t)=∑Ais(t-iT-τi)+n(t)

(1)

其时域信号波形如图1所示。

利用循环平稳对该振动信号进行分析，可以得到滚动轴承的时变自相关函数Rx(t,τ)为

φτ(t)+Rn(τ)

(2)

式中：Rn(τ)为平稳随机噪声的自相关函数；φτ(t)为τi的概率密度函数。

谱相关密度函数为

对式(3)分析可知，非零谱相关密度对应故障发生频率α及其倍频和以调制频率为间距的边频带成分。由此可以得出滚动轴承不同部位点蚀故障振动信号的循环平稳特征频率，其结果见表1。其中：fop、fip、fbp分别为滚动轴承外圈、内圈、滚动体的通过频率；fr、fcc分别为轴承的转频和保持架转频；n、k为正整数。

表1 滚动轴承的循环平稳特征频率

通过谱相关密度函数的α-f平面表示故障特征，不仅能够表示轴承的故障特征频率，还能表示特征频率对应的信号能量分布(如图2所示)。

自循环平稳被用于滚动轴承故障诊断以来，取得了许多成就，研究者从不同的角度提出了不同的故障诊断方法。根据表示信号周期性的统计特征不同，循环平稳随机过程分为一阶、二阶和高阶，但用于滚动轴承故障诊断的主要是二阶循环平稳和高阶循环平稳。

2 二阶循环平稳

若随机过程x(t)的自相关函数Rx(t,τ)(即该随机过程的二阶矩)满足：

(4)

则称x(t)二阶循环平稳。

二阶循环统计量主要包括循环自相关函数、谱相关密度函数、谱相干密度函数等。

(5)

(6)

谱相干函数ρuv(f)：

(7)

基于二阶循环统计量的滚动轴承故障诊断主要有以下几个方面研究。

(1)循环平稳信号的时频分析。为了提高抑制噪声的能力，同时又不增加计算量，将循环平稳信号在时频域进行分析，以期达到更好的效果。Urbanek等[7]提出了一种能提取不同运行速度及不同载荷下振动信号中的二阶循环平稳成分的时频分析方法。王宏超等[8]对谱相关分析方法加以改进，提出了一种集成改进谱相关(integrated improving spectrum correlation, IISC)分析方法，相对于改进谱相关方法，IISC方法只提取调制频率而忽略载频，具有更直观的效果，同时还具有更强的抗噪能力。

(2)与其他方法结合。将不同的诊断方法相结合，发挥不同方法的优点。Girondin等[9]将循环自相关、小波分析与支持向量机相结合用于滚动轴承特征提取。徐亚军等[10]将线调频小波路径追踪算法与阶比循环平稳解调法相结合，对变转速工况的滚动轴承进行故障诊断。

(3)循环平稳分析效率的提高。循环平稳分析的缺点在于其计算量大，耗费时间长，不利于快速诊断，限制了其在实际中的应用。柳亦兵等[11]应用对数谱相关函数灰度值能够反映信号中的随机成分对循环平稳特性的影响，定性判断故障引起的谱相关函数中的随机成分的变化，通过共振区切片进行故障解调分析。Ming等[12]在FFT变换的基础上研究了谱自相关分析，相比于其他循环平稳故障特征频率提取方法，其运算时间短。

二阶循环统计量自身良好的解调性能，使其成为常用的滚动轴承故障诊断方法之一。但是，基于二阶统计量的特征提取方法也存在自身的缺陷。

(1)Wigner-Ville时频分布会存在交叉干扰项，影响特征提取的准确程度；

(2)自相关函数可以很好地描述平稳高斯过程，但是对非高斯过程无能为力；

(3)故障发生早期振动信号的冲击幅值很低，故障信息淹没在噪声和干扰信号中，二阶循环分析对噪声敏感，难以从实际信号中提取有效信息。

相比于二阶循环统计量，高阶循环统计量在信号处理中不仅可以保留信号的相位信息，还具有对高斯和非高斯噪声的自然免疫功能，十分有利于分析非平稳、非高斯信号，使得高阶循环平稳成为轴承状态监测和故障诊断的重要方法。

3 高阶循环平稳

高阶循环统计量是以循环平稳信号的高阶统计量为理论基础发展起来的，因此高阶循环统计量具有高阶统计量和循环平稳统计量的优点。其主要是指高阶循环矩、高阶循环累积量以及对应的高阶循环矩谱、高阶循环累积量谱。

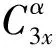
(8)

循环双谱的阶次最低，计算相对简单，但它具有高阶循环累积量谱的所有优点，能够分析滚动轴承的循环平稳特性，抑制信号的高斯和非高斯噪声。目前，高阶循环平稳在滚动轴承故障诊断方面的研究主要有两点。

(1)故障特征的表示。高阶循环统计量是含有多个参变量的多维函数，难以用传统的谱分析方法清楚、直观地表达故障特征，因此，将高阶循环平稳用适当的方式用于故障特征提取是研究的重点之一。周宇等[13]尝试用循环双谱的中心频率的切片谱对滚动轴承的早期故障进行特征提取。

(2)计算效率的提高。高阶循环平稳虽然具有非常好的优点，但是它需要较大的数据采集量，且计算复杂，限制了其在实际中的应用。因此，在利用高阶循环平稳的同时，必须考虑如何降低其计算量，提高计算效率。唐贵基等[14]将局部均值分解和切片双谱相结合对滚动轴承进行故障诊断，利用了高阶谱抑制噪声的优点，同时也降低了计算量。Dong等[15]提出了频率—轴双谱方法，比循环双谱更适合分析幅值和频率调制信号，并在故障诊断的准确性和计算效率方面得到提高。

前述的二阶、高阶循环平稳滚动轴承故障诊断方法都是建立在转速稳定或小范围波动的前提下，但在实际中，大部分机械都是运行在变转速或者变载荷的条件下，上述方法难以有效识别故障。相比于稳定工况，变转速下的振动信号变得更复杂[16]，轴承载荷和转速的变化都会引起振动信号的调制现象，增加了轴承故障诊断的难度。

4 角度/时间循环平稳

近年来，许多学者致力于将循环平稳方法应用到变转速工况轴承故障诊断。李蓉等[17]将阶次分析和循环平稳解调相结合，实现了变转速工况下齿轮箱复合故障的诊断。Abboud等[18-20]提出了角度/时间循环平稳(angle/timecyclostationary,ATCS)方法，将角度/时间自相关函数(angle/timecovariancefunction,ATCF)进行双重傅里叶变换，得到阶频谱相关(order-frequencyspectrualcorrelation,OFSC)，能够表现调制信号和载波信号能量的阶频分布，用于表征轴承故障特征。

4.1ATCS信号

如果振动信号的ATCF具有周期性，并且在循环阶处存在非零傅里叶系数，那么这个信号是ATCS信号。其振动模型为

(9)

ATCS信号模型示意图如图3所示。

4.2 角度/时间循环平稳分析

在循环平稳统计量中将时间和角度联合表示，得到ATCF：

C2x(θ，τ)=E{x(t(θ))x(t(θ)-τ)}

(10)

ATCF描述了循环调制的过程，通过角度变量和由时间延迟变量携带的载波特征的平均来描述。

对于ATCS信号， ATCF是关于变量的严格角度周期函数，因此在循环阶i时的非零傅里叶系数为

(11)

和循环谱相关类似，阶频谱相关被定义为ATCF的二次傅里叶变换，第一次傅里叶变换将角度(弧度)映射到阶(没有单位)，第二次傅里叶变换将时间(秒)映射到频率：

(12)

式中αθ为阶，表示轴每旋转一周某事件发生的次数。

式(12)可以通过时域信号计算得到：

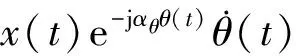
(13)

对于ATCS信号，其OFSC为

S2x(αθ，f)=Sxxαθ(f)

(14)

可以将阶频谱相关理解为信号x(t)和xαθ=x(t)ejαθθ(t)θ(t)W/Φ谱相关密度函数。

由阶频谱相关可以得到信号的阶频图，其中的循环阶显示了波形中的循环信息，用来表示故障信息；将与理论计算的故障阶次进行对比，即可判断出该振动信号的故障类型，实现变转速工况下的滚动轴承故障诊断，其诊断流程如图4所示。它与传统循环平稳分析的区别如图5所示。

ATCS分析扩展了循环平稳理论在滚动轴承故障诊断中的应用，成为循环平稳理论滚动轴承故障诊断研究的新方向。

5 结 论

(1)二阶循环平稳是滚动轴承故障特征提取常用方法，能够有效解调故障振动信号，提取故障信息。但其抑制噪声的能力有限，且在时频分布的应用中难以抑制交叉干扰项，限制了其在滚动轴承故障诊断中的应用。

(2)高阶循环平稳分析自身具有良好的噪声抑制能力，克服了二阶循环平稳方法的不足，但其故障特征表示方法和计算效率还有待更多研究。

(3)在循环平稳理论基础上提出的角度/时间循环平稳分析，实现了变转速工况下滚动轴承故障诊断，具有广阔的应用前景，已经成为循环平稳理论在滚动轴承故障诊断研究中的新方向。

[1] 夏均忠,刘远宏,但佳壁,等.基于EMD分形技术提取变速器轴承故障特征[J].噪声与振动控制,2012,4(2):119-127.

[2] 王宏超,陈进,董广明.基于谱相关密度组合切片能量的滚动轴承故障诊断研究[J].振动与冲击,2015,34(3):114-117.

[3] ABBOUD D, ANTONI J, ELTABACH M, et al. Deterministic-random separation in nonstationary regime[J]. Journal of Sound and Vibration, 2016,362(3):305-326.

[4] MCFADDEN P D, SMITH J D. Model for the vibration produced by a single point defect in a rolling element bearing[J]. Journal of Sound and Vibration, 1984,96(1): 69-82.

[5] ANTONI J, RANDALL R B. A stochastic model for simulation and diagnostics of rolling element bearings with localized faults[J]. Journal of Vibration and Acoustics, 2003,125(3): 282-289.

[6] ANTONI J. Cyclic spectral analysis of rolling-element bearing signals: facts and fictions[J]. Journal of Sound and Vibration, 2007,304(3-5): 497-529.

[7] URBANEK J, BARSZCZ T, ZIMROZ R, et al. Application of averaged instantaneous power spectrum for diagnostics of machinery operating under non-stationary operational conditions[J]. Measurement, 2012, 45(7): 1782-1791.

[8] 王宏超,陈进,霍柏琦,等.强抗噪时频分析方法及其在滚动轴承故障诊断中的应用[J].机械工程学报,2015,51(1):90-96.

[9] GIRONDIN V, PEKPE K M, MOREL H. Bearings fault detection in helicopters using frequency readjustment and cyclostationary analysis[J]. Mechanical Systems and Signal Processing, 2013,38(2):499-514.

[10] 徐亚军,于德介,刘坚.基于线调频小波路径追踪阶比循环平稳解调的滚动轴承故障诊断[J].航空动力学报,2013,28(11):2601-2608.

[11] 柳亦兵,辛卫东,李宏,等.滚动轴承故障的谱相关特征分析[J].中国机械工程,2013, 3(2): 351-355.

[12] MING A B, QIN Z Y, ZHANG W, et al. Spectrum auto-correlation analysis and its application to fault diagnosis of rolling element bearings[J]. Mechanical System and Signal Processing, 2013,41(1):141-154.

[13] 周宇,陈进,董广明,等.基于循环双谱的滚动轴承故障诊断[J].振动与冲击,2012,31(9):78-81.

[14] 唐贵基,王晓龙.基于局部均值分解和切片双谱的滚动轴承故障诊断研究[J].振动与冲击,2013,32(24):83-88.

[15] DONG G, CHEN J. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings[J]. Mechanical System and Signal Processing, 2012,33(11):212-236.

[16] 林京,赵明.变转速下的机械设备动态信号分析方法的回顾与展望[J].中国科学:技术科学,2015,45(7): 669-686.

[17] 李蓉,于德介,陈向民,等.基于阶次分析与循环平稳解调的齿轮箱复合故障诊断方法[J].中国机械工程,2013,24(10):1320-1327.

[18] ABBOUD D, ANTONI J, ELTABACH M, et al. Angle/time cyclostationarity for the analysis of rolling element bearing vibrations[J]. Measurement, 2015,75(11): 29-39.

[19] ABBOUD D, BAUDIN S, ANTONI J, et al. The spectral correlation analysis of cyclo-non-stationary signals[J]. Mechanical System and Signal Processing, 2016, 75(6): 280-300.

[20] ABBOUD D, ANTONI J. Order-frequency analysis of machine signals[J]. Mechanical System and Signal Processing, 2017,87(3): 229-258.

(编辑：张峰)

Application of Cyclostationary in Rolling Bearing Fault Diagnosis

WANG Zhian1, XIA Junzhong2, DAN Jiabi2, YU Mingqi1, LYU Qipeng1

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China; 2.Military Vehicle Department, Military Transportation University, Tianjin 300161, China)

To explore the application principle and research status of cyclostationary in rolling bearing fault diagnosis, the paper firstly discusses the demodulation principle of cyclostationary on rolling bearing fault vibration signal. Then, it studies the application of second-order cyclostationary and higher-order cyclostationary in rolling bearing fault diagnosis, and analyzes its advantages and disadvantages. Finally, it elaborates the fault diagnosis method for rolling bearing named angle/time cyclostationary under the condition of variable speed. The result shows that the application of higher-order cyclostationary and angle/time cyclostationarity is one of the research directions for rolling bearing fault diagnosis.

rolling bearing; fault diagnosis; cyclostationary; higher-order cyclostationary; angle/time cyclostationary

2017-01-01；

2017-01-13．

汪治安(1992—)，男，硕士研究生； 夏均忠(1967—)，男，博士，教授，硕士研究生导师.

10.16807/j.cnki.12-1372/e.2017.06.007

TH133.33

A

1674-2192(2017)06- 0025- 06