基于多因子模型的量化选股分析

徐景昭

摘 要：基于量化投资中常用的多因子模型，对使用较为广泛的11个因子利用回归法进行有效性检验，选出有效因子分别构造了适合一般投资者使用的基本多因子模型、基于货币周期的行业轮动多因子模型以及基于固定效应下的多元回归模型。通过实证分析比较不同模型间所构建的投资组合的收益率与市场收益率，验证了量化选股策略的有效性，也为不同层次的投资者提供了研究数据与选股策略。

关 键 词：量化投资；多因子模型；行业轮动效应；多元回归分析

中图分类号：F830.91 文献标识码：A 文章编号：2096-2517（2017）03-0030-09

Analysis on Quantitative Investing Strategy Based on

Multi-factor Model

Xu Jingzhao

（Jiangxi University of Finance and Economics， Nanchang 330013， China）

Abstract： Based on the multi-factor model commonly used in quantitative investment， this paper uses the regression method to test the validity of 11 factors， then selects some effective factors to construct the basic multi-factor model， which is suitable for the ordinary investors. Moreover， based on the monetary cycle and the multiple regression models on the fixed effect， the paper compares the yield and market rate of return of the portfolio constructed by different models through empirical analysis， demonstrates the effectiveness of the stock selection strategy， and provides the research data and stock selection strategy for different investors.

Key words： quantitative investment； multi-factor model； industry wheeling effect； multiple regre-ssion analysis

隨着中国资本市场复杂程度日渐加深和规模日益庞大，投资品种和数量与日俱增，无论是个人或是机构投资者所拥有的投资渠道与投资方法也在逐渐增多。量化投资作为一种来自海外资本市场的先进技术，在海外资本市场中受到了广泛追捧，著名的西蒙斯与大奖章基金便是利用了量化投资技术，于1989～2007年间获得了高达38.5%的平均年收益率。 中国的量化投资发展虽仍在起步阶段，但越来越多的投资人开始研究量化投资，试图通过数学、金融学、计算机科学相结合的优势来寻求超额收益。据统计显示，截至2016年10月，中国公募基金中共有48支基金以“量化”命名，其中长信量化先锋基金（519983），申万菱信量化小盘股票基金（163110）与大摩多因子策略混合基金（233009）等均表现出色，具有较高的年化收益率。而无论是在个体投资或是基金投资中，多因子选股模型均是较为广泛的量化模型之一。本文基于多因子模型策略，利用2011～2015年的数据对投资过程中的常用因子进行有效性检验，并使用有效因子构建基本多因子模型，根据假设创造性地使用简单打分法构建投资组合，基于2014～2016年的历史数据进行实证分析， 为广大一般投资者提供了一种简单可行且收益率超过市场表现的投资策略。最后结合行业轮动效应与面板数据的多元回归分析对基本模型进行了深化与修正，创新性地提出了基于多因子模型的更多投资策略，也为较深层次的理论研究者提供了思路与数据参考。

一、文献综述

关于量化投资选股策略的研究涉及许多方面，常见的包括多因子模型、风格轮动模型、动量反转模型、趋势追踪模型等。对于多因子模型，最重要的环节便是有效因子的选取。大多数论文对于有效因子的选取通常采用因子评分法，此方法最早由Piotroski（2000）提出，常见操作为：将股票池中的股票按N个候选因子的大小依次排序， 按照每个排序选取排名靠前的股票等权重构建N个极端的股票组合持有到期末， 计算N个组合的平均收益率并与基准的指数收益率进行比较，用此方法能成功获取alpha收益组合所使用的排序因子即为有效因子[1]。另外一种方法则是回归法，通过计量模型求得单个因子对股价波动的贡献与显著性。丁鹏曾在其《量化投资——策略与技术》一书中使用1997～2006年的历史数据对常用的因子进行了有效性检验[2]，大多数检验多因子模型的论文所使用的数据也均在2012年前。本文所选数据在2011～2016年间，更具有时效性，且本文在选取有效因子的部分中采用Fama-Macbeth regression的基本思路，对候选因子进行时间序列回归，再对得到的所有β值求t统计量检验其显著性，通过检验的即为有效因子。关于行业轮动效应的研究，有学者将行业轮动与多因子模型相结合，对基于经济周期的行业板块轮动效应进行了实证分析，后续相关文章也大多照此思路，运用宏观经济指标来调整不同行业间的权重。本文在吸取前人研究的基础上，结合最新的货币周期动态，提出以货币增速剪刀差为分界点的行业轮动策略，并使用2014～2016年的最新数据进行了实证分析。

二、多因子模型的理论基础

多因子模型的建立主要在CAPM模型、APT模型等理论的基础上逐步演化而来[3]。CAPM模型在非常严格的假定下，通过构造资本市场线方程E（rp）=rf+■？滓p与证券市场线方程E（ri）=rf+[E（rm）-rf]？茁i，说明了有效组合的期望收益率包括无风险收益率和市场风险的价格与组合标准差的乘积， 对有效组合的风险度量指标则是组合的标准差； 而对风险证券的期望收益率也包括两个部分，即无风险收益率和？茁值与市场风险溢价的乘积，对风险证券的风险度量指标则是β值。

套利定价理论APT模型放宽了CAPM模型的严格假定，可以通过下式表示：

ri=？琢i+？茁i1F1+？茁i2F2+……+？茁inFn+？着i

其中，ri表示任意一种证券i的实际收益率；？茁i表示证券i相对于k因素的敏感度；？着i表示误差项，也可以认为是只对个别证券收益起作用的非系统因素；Fn表示对所有资产都起作用的共同因素。APT模型不仅放宽了CAPM模型过于严格的假定，也为后来多因子模型的发展奠定了基础。例如之后问世的Fama-French三因素模型，可以通过下式表示：

E（ri）=rf+？茁iE（rm-rf）+s1E（SMB）+h1E（HML）

它使用了风险值、市值因子和账面价值比三因素来衡量对金融资产收益的影响，并且得到了很好的验证。然而，对于如今资本市场日趋复杂的趋势，仅仅运用三个因子不足以衡量当今市场的变化波动，还有许多因子会共同作用于证券投资的收益率。于是Fama和French于2015年提出Fama-French五因子模型[4]，可以通过下式表示：

E（ri）=？琢i+？茁i（rm-rf）+siE（SMB）+hiE（HML）+

riE（RMW）+ciE（CMA）+？着i

在三因素的基础上增加了盈利能力RMW与投资水平CMA两个因素，修正了原模型的不足。本文通过将量化分析中的常用因子分为价值因子、成长因子、质量因子和动量因子四类，并通过有效性检验来筛选因子，构建模型与投资组合。

三、候选因子与有效性检验

首先使用多因子模型将量化投资中的11个常见因子按价值因子、成长因子、质量因子、动量因子进行划分，如表1所示。

本文采用的数据均来源于Wind资讯，对2011～2015年间每一年的数据，用沪深300中的所有股票涨跌幅对每只股票对应的检验因子进行时间序列回归，公式如下：

yt+1=？琢t+？茁txt+？着t

得到每只股票涨跌幅对各因子的回归系数？茁i（i=1，2，3，……，300）后，剔出异常值和缺省值的影响，对有效的所有β值在5%的显著性水平下进行t检验（H0∶ ■=0；H1∶ ■≠0），结果如表2所示。

可见，在2011～2015年间的中国股市中，较为有效的因子有市盈率、市净率、净资产收益率增长率、资产负债率与月平均换手率。由于市盈率与市净率同属于价值因子部分， 为了追求基本模型的简单明确，防止冗杂因子出现，比较之下本文选择市净率作为价值因子代表， 成长因子中选择ROE增长率为代表， 质量因子中选择资产负债率为代表，动量因子中选择月平均换手率为代表，用以构建后续的基本模型。

四、基本的多因子模型构建与实证分析

重新回顾Fama-French三因素与五因素模型，两个模型在多次修正与检验中都坚持使用了一个重要的影响收益的因素——市值。从上文的有效检验来看市盈率（即市值/净利润）就是一个严格负相关的有效因子。 从现实来看，A股市场的投资者结构表明，大多数投资者的确是对高市盈率、总市值大的股票避而远之， 对该类股票不拥有持有的信心，甚至具有较强的看跌预期。本文选用市净率作为价值因子的代表，但是考虑到市盈率与市值的影响，本文将市值加入多因子选股策略中，强调选择股票池中市值较小的股票进行优先投资，结合上文中提到的另外四个有效因子，构建基本的多因子模型如下：

E（ri）=rf+？茁1E（ROEg）+？茁2E（DAR）+？茁3E（PB）+

？茁4E（MV）+？茁5E（MTO）+？着

其中，PB代表市净率，MV代表总市值，MTO代表月平均换手率， 从上文的因子有效性分析可知，这三个因子与投资组合预期收益存在负相关关系；ROEg表示净资产收益率的同比增长率，DAR表示资产负债率， 与投资组合预期收益存在正相关关系。该因子模型的选股思路在于，选用ROE增长率与资产负债率作为两个有效因子挑选符合条件的股票同时，考虑到市值、市净率与月平均换手率对收益的负作用，在进行比较时倾向选择总市值小、市净率低且换仓月平均换手率较低的股票建立投资组合。

首先， 采用简单打分法进行投资组合的構建。按照每个因子值进行排序，正相关的因子按降序排列，负相关的因子按升序排列，并按照该排序给沪深300中的每只股票从1到300给每项因子排序并依次打分，最后将5项因子得分的平均成绩按升序排列， 股票得分越低表示在该模型上的表现越好。注意，此处打分法中最后的平均得分是基于因子等权重的假设，目的是方便一般投资者能简单运用该模型进行选股策略，同时也为了验证量化选股的强有效性。后文中会放开该假定重新计算不同因子的各项权重。

其次，考虑组合中的股票个数。根据Fama对资产组合中证券数量与资产组合风险关系的实证分析结论可知，最初几种股票加入资产组合时能显著降低组合标准差，但当股票数量增加到20种时，再增加证券就不能明显降低资产组合标准差。所以本文在剔除缺省值与极端值影响的情况下， 选取得分表现最好的前20只股票构建资产组合， 半年进行一次调仓。由于进行因子打分时需要使用上市公司半年报与年报的相关披露数据，根据相关法律规定，上市公司年度报告的披露不应当晚于次年的4月30日， 半年度报告的披露不应当晚于当年的8月31日。因此，将实证分析的起始时间定于2014年11月1日， 半年调仓时间为2015年4月23日左右，该时间已确保了在进行调仓时上市公司的数据已披露，所构建的投资组合如表3所示。

本文选取2014年11月1日至2016年11月4日的历史数据对投资组合的收益进行实证分析。选取该时间段的原因是： 首先该数据时效性较强，可证明该模型在现今中国股市中的有效性；其次考虑到该时间段经历了牛市开始、牛市顶点、牛熊市切换、熊市低点与市场回升五个阶段，具有比较全面的覆盖性，可以得出该模型在市场的不同阶段的具体表现。选用的基准指数为沪深300指数，比较沪深300指数收益与多因子模型所构建的资产组合在2年内收益，具体操作为：每半年视为一期，每期采用相同的初始资金，每期初均对投资组合的股票进行等金额的投资，半年后清仓并调仓，比较每期投资组合与同期沪深300指数的持有至到期收益，如图1、图2和表4所示。

由多因子选股模型运行结果和基准收益率的趋势对比我们可以看出， 当股市处于牛市行情时（2014.11～2015.5）， 多因子选股模型相对于基准收益率而言有极好的表现，半年间持有至收益率高达135.05%，远高于基准收益率89.35%，说明该模型在牛市的环境下选股能力比较强。当股市处于牛熊市切换时（2015.6～2015.11），该模型开始时同样有较好的表现，半年累计收益率维持在-16.7%，相对于指数在牛熊市切换时产生的大幅下跌（-25.6%），该模型在该阶段表现出较强的防御能力。当市场进一步下跌处于熊市低点时（2015.11～2016.2），该模型在前半段时间仍表现出很强的防御能力，但后期市场开始出现反弹行情时（2016.2～2016.5），略低于基准收益率，不过差别较小。而一旦市场出现持续较强反弹回升的行情时（2016.6～2016.11），该模型也能成功获得较高超额收益。

总体来看， 该多因子选股模型在样本期间总体表现较为优异， 但当该投资收益相对应的波动率超过了市场的总体水平时， 该模型仍存在一定风险。且该模型的选用具有较强的阶段性，适合在整体股市进入牛市、牛熊市切换或是出现较强反弹行情时使用， 但在市场出现剧烈波动时有效性有所下降。

五、基于行业轮动效应的多因子模型修正

根据行业轮动模型来看，自上而下的投资分析方法认为，宏观经济决定了资产的收益率。所以投资者应先关注宏观经济运行状况再进行资产配置或是调整投资组合的风格。利用宏观经济指标驱动行业配置的理念与作用在行业因子中也是股票收益的重要贡献因子，通过行业层面分析，选择适合当前经济运行状况的行业进行配置，获得超额收益的概率也会较高。当宏观经济指标下行时，应投资于非周期性行业；当宏观经济指标上行时，则投资于周期性行业。

而中国资本市场的投资者在近几年来经常参考的一个宏观经济指标便是货币政策与货币周期。狭义的货币政策股市传导机制由Chami等（1999）提出，主要分析了货币政策影响通货膨胀率而导致股东权益变化进而引起的投资变化；广义的货币政策传导机制认为货币政策影响股市的两个重要操作指标是利率和货币供应， 通过资产替代效应、预期效应、成本效应、股票定价效应等一系列机制影响股票市场[5]。可见掌握货币政策，分析货币周期的确对投资者的资产配置有着一定的指导意义。我国的货币政策主要通过中央银行调整存款准备金率、调整再贴现率与公开市场操作等手段来控制货币供应量。我国现行的货币统计制度将货币供应量划分为三个层次：

第一，流通中现金（M0），指单位库存现金和居民手持现金之和。

第二，狭义货币供应量（M1），指M0加上单位在银行的可开支票进行支付的活期存款。

第三，廣义货币供应量（M2），指M1加上单位在银行的定期存款和城乡居民个人在银行的各项储蓄存款以及证券公司的客户保证金。

统计2014～2016年中国M1与M2的同比增长率，如图3所示。

结合我国的货币政策来看， 自2014年11月22日中国人民银行采取非对称方式下调金融机构人民币贷款和存款基准利率开始，我国央行连续在2015年中进行了6次降准降息。表现为我国M1增速自2015年3月开始保持稳步上升趋势，从M1与M2的增速差来看，2015年10月出现货币增速剪刀差。根据相关文献论证，货币增速剪刀差与宏观经济变量之间存在着相关关系，宏观经济指标的改善会在一定程度上提高货币活化度，导致货币增速剪刀差扩大；同时货币增速剪刀差会进一步引起宏观经济指标的改善，实证分析也表明货币增速剪刀差与国内生产总值同比增速呈现正相关关系[6]。可见，货币增速剪刀差的出现一定程度上体现了宏观投资环境的改善。结合行业轮动效应可以认为，货币增速剪刀差的出现与消失均可以作为进行行业轮动调整的信号： 在2014.11～2015.10这一时段货币周期仍处于较为紧缩的状态，应倾向投资于非周期性行业； 在2015.11～2016.11这一时段属于货币周期的扩张阶段， 应多考虑选择周期性行业。 根据William·F·Sharp市场模型来看， 单个证券或一个投资组合的收益率与市场指数的收益存在一定关系，其相关系数定义为β值， 当β>1时， 可称为进攻性证券；β<1时，则是防御型证券。同样，我们将一个行业中的所有股票看作一个投资组合，其收益对市场指数的敏感性也可以用β表示，β>1时， 可定义为周期性行业；β<1时，则是非周期性行业。对于每个行业的β值可采用单因素模型进行测算，具体公式为：

Y=？琢+？茁X+？着；？茁=■

其中，y为沪深300指数收益率序列数据，x 为行业指数收益率序列数据，n为区间内根据时间频度决定的收益率个数，此处均采用年化数据进行计算。行业划分按照Wind一级行业划分，行业指数使用Wind资讯行业指数， 计算出以沪深300为样本数据的行业β值，如表5所示。

根据前文所选出的投资组合，进行考虑行业β值与货币周期后的仓位调整：当货币周期处于紧缩时，赋予β值较小的行业较高的仓位，当货币周期处于扩张时，则做相反处理，具体仓位计算如下：

紧缩时：wi=■×0.05（i=1，2，3，……，10），

？姿t=1/∑wi，Pit=？姿twi

扩张时：wi=？茁i×0.05（i=1，2，3，……，10），

？姿t=1/∑wi，Pit=？姿twi

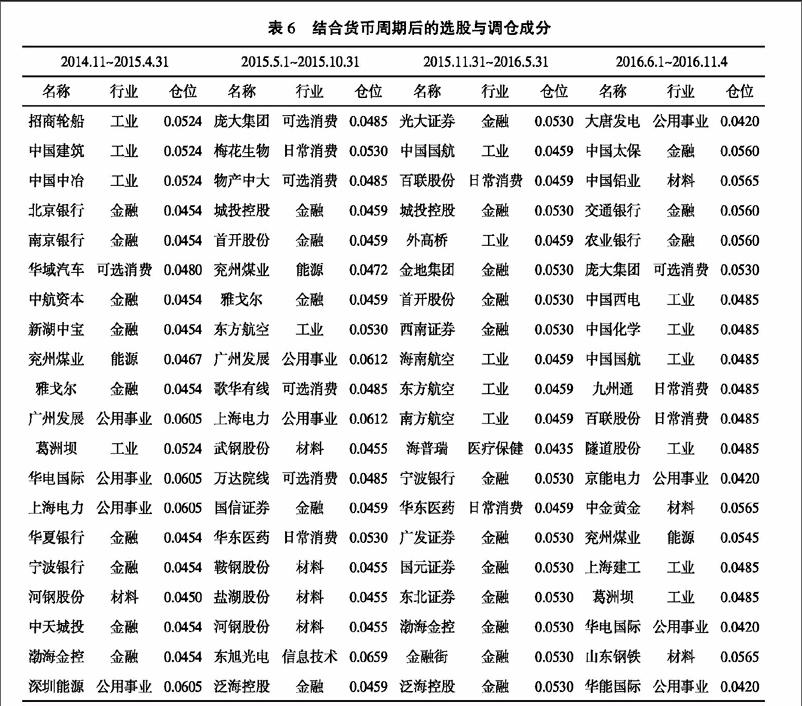
其中，？茁i表示第i个行业的？茁值，wi为第i个行业考虑行业轮动后的平均仓位，？姿t为第t期的调整因子，Pit为第i个行业在t期的具体仓位。根据计算可得基于行业轮动的投资组合调整结果，如表6所示。

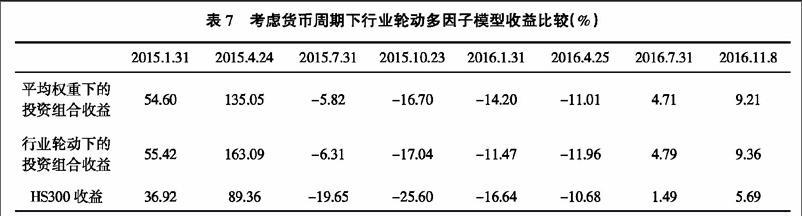
将平均仓位下的投资组合与行业轮动下的投资组合收益在同一时期进行持有至到期收益率的实证对比，结果如表7所示。

综合来看，加入行业轮动效应后修正的多因子选股模型虽然不能保证在每一个时间点均获得比基本多因子模型高的超额收益，但是在近两年的投资期中的确能收获更高的平均收益率，且表现结果也能超过市场收益。可以证明，中国股市在近期内的确存在着较为明显的行业轮动效应，加入行业轮动调仓的确能增强多因子模型获得超额收益的能力，同时也验证了量化选股的各项策略间存在互补关系。

六、基于多元回归分析的多因子模型修正

在前文的基本多因子模型中曾使用简单的打分法，假设因子同权重时对股票池中的股票进行排序打分建立投资组合。但现实中每个因子对收益率的贡献一般不会出现均等情况。 为了修正该假设，本文采用构建面板数据进行多元回归分析的方式来比较因子间的权重大小。 具体操作为： 利用2012～2015年间的历史数据建立短面板数据，由于不同因子间的量纲差距较大，先对单项因子进行线性标准化处理，即通过数学变换将各因子的取值换算为（0，1）内的数字来解决因子间的不可公度性，计算公式为：

X■■=■

其中，i代表不同因子（i=1，2…5），xi为各项指标的原始值，min（x）与max（x）分别代表该因子的最小值与最大值，X■■表示该因子的标准化值。将数据进行标准化处理后，构建以下计量模型对原多因子模型进行修正：

CHGnt+1=？茁0+？茁1ROEgnt+？茁2DARnt+？茁3MTOnt+？茁4PBnt+

？茁5MVnt+an+unt

其中，n代表沪深300中不同股票的观测值（n=1，2，…，300），t代表时间。CHGnt+1为股票在下一期的涨跌幅；ROEgnt代表净资产收益率的同比增长率；DARnt代表资产负债率；MTOnt为月平均换手率；PBnt为市净率；MVnt代表总市值；an为非观测效应，概括了影响着CHGnt但又不随着时间而变化的因素；unt为特异性误差。

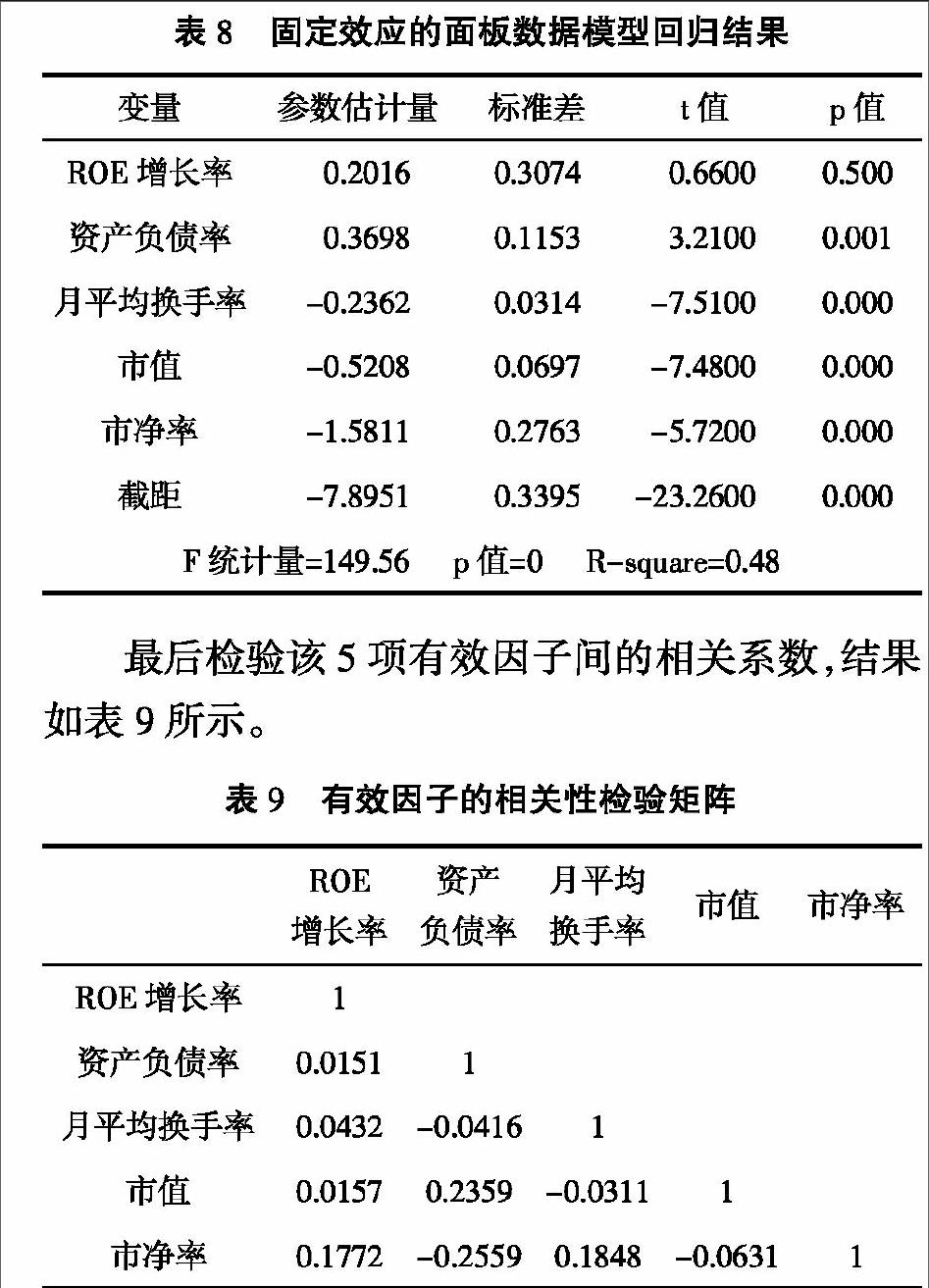
在使用该模型进行回归分析前，对该模型进行Hausman检验来确定是使用随机效应模型还是固定效应模型更为有效。Hausman检验结果表明p=0， 强烈拒绝随机效应模型会提供一致性估计的原假设， 因此决定采用固定效应模型进行回歸分析。为避免异方差性，在回归前对各变量进行取对数处理，回归后结果如表8所示。

最后检验该5项有效因子间的相关系数，结果如表9所示。

取阈值为0.5， 由数据可证明并未有两两因子间出现较高的相关系数，证明最初的基本多因子模型并未有冗杂因子，该多元回归模型也不存在多重共线性。

通过面板数据的计量模型实证分析来看，净资产收益率同比增长率与资产负债率的确均与股票涨跌幅存在正相关性，且资产负债率对股价涨跌仍存在显著性影响。但净资产收益率的同比增长率虽然通过了单因子回归的有效性检验，但在多元回归模型中并未通过显著性检验；而月平均换手率、市净率与总市值则与前文描述一致，存在严格的负相关性。由于篇幅原因，本文在此未做实证分析，而是根据这一结果对前文的打分法提出如下两种修正策略，供投资者参考：

第一，在进行打分法排序时加入因子权重的具体数值，具体计算为：单个因子得分Si=？茁i·R。其中i表示不同有效因子，？茁i为不同因子由多元回归模型所计算出的权重，R为排名得分（R=1，2，…，300），通常正相关因子按升序排列给予1～300得分，负相关因子按降序排列给予1～300得分，每只股票总得分为∑Si，根据∑Si选出得分最高的20只股票构建投资组合。

第二，综合比较多元回归的因子权重？茁i，以及显著性检验统计量|t-value|的绝对值大小， 对影响最大的因子进行优先筛选，影响越小的因子筛选顺序越靠后。例如在本文模型中的具体操作为：选出有效因子中影响最大的因子并按其值在沪深300股票池中优先筛选出前100只股票，再按照第二有效因子的排序筛选出前60只股票，第三、第四、第五有效因子分别选出前40、前30、前20只股票，最后筛选出的20只股票即为构建的投资组合。

七、结论

本文以量化投资中最常用的多因子模型为基础，从一元回归对因子进行有效性检验开始，筛选出近年来从数据上较为有效的因子，构建了基本的多因子模型，采用简单打分法为广大投资者提供了一个简单可操作、无需太多复杂整理运算的选股策略，并放入近期的市场中，用历史数据验证了该多因子选股模型的投资效果的确高于市场的表现，从而证明了量化选股策略的强有效性。随后进一步修正了多因子模型，从货币周期的角度出发验证了中国股市近年来存在的行业轮动效应，启发了投资者在构建资产组合或分配仓位时要考虑宏观经济指标与行业因素；再加入较为复杂的面板数据多元回归，使用固定效应估计法，在模型中修正了各有效因子的权重，为较深层次的理论研究者与量化投资者提供了相关数据与分析思路。

总体来看，量化投资依靠较大的数据量与科学的数理统计相关运算，的确能提供寻求超额收益的有效策略，同时也证明了量化投资在中国股票市场具有很强的可行性与市场潜力，多因子模型只是量化投资策略中的简单一种，还有更多丰富的策略等待广大的投资者去验证与修正。肯定的是，量化投资会随着中国资本市场的复杂深化而日渐普及。

参考文献：

[1]PIOTROSKI，J D. Value Investing： The Use of Historical Financial Statement Information to Separate Winners from Losers[J]. Journal of Accounting Research，2000（38）.

[2]丁鹏.量化投资——策略与技术[M]. 北京：电子工业出版社，2012.

[3]桂荷发，吕江林. 证券投资理论与实务[M]. 北京：高等教育出版社，2012.

[4]FAMA，E F，FRENCH K R. A Five-Factor Asset Pricing Model[J]. Journal of Financial Economics，2015（116）.

[5]CHAMI R，COSIMANO T F，FULLENKAMP C. The Stock Market Channel of Monetary Policy[J]. Social Science Electronic Publishing，1999（22）.

[6]范立夫，周亚，史欣沂. 货币增速剪刀差与宏观经济关系的实证研究[J].宏观经济研究，2016（8）.

（责任编辑、校对：李丹）