提问到位 激活思维
陈玉红
数学课堂教学中,如何设计问题,激发学生思维,使学生通过主动学习融会贯通地掌握知识,形成能力,是值得深入探索的一个课题。笔者在听课过程中,发现教师提问常用的是简单的一问一答的方式,没有真正启发学生的思维,引发深入的思考。教师在教学中的提问要到位,才能激活学生的思维。
一、设计适度的问题,培养学生敏捷的思维能力。
教学实践表明:学生的思维是否敏捷,一个重要的因素是看老师在教学过程中设计的问题是否适度。这里所说的适度,就是指设计的问题符合绝大多数学生的认知水平和知识能力。设计的问题适度,有利于激发学生的兴趣和思维的积极性,培养学生敏捷的思维能力。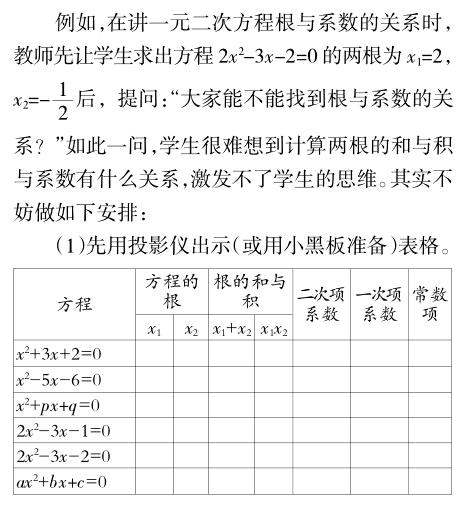
(2)要求学生先填前两个二次项系数为1的方程部分的内容。
(3)教师再提问:观察它们的根与一次项系数、常数项之间有什么共同的规律?然后让学生猜想方程x2+px+q=0的两根之和、两根之积。
(4)用同样的方法观察第二组中二次项系数不是1的方程,再提问:能否得出相同的结论?最后师生共同归纳出一般结论。
这样设计的问题照顾到了学生的接受能力,由易到难,由简单到繁杂,由浅入深。学生回答问题踊躍,思维敏捷,在获得发现的喜悦感和成功的满足感的同时也提高了对数学学习的兴趣。
二、设计开放性问题,培养学生的求异思维能力。
求异思维就是不墨守成规,寻求变异,随时注意变换角度思考,通过活跃的思维达到求异、求佳、求新。教师在教学中,除有计划、有目的地设计一些一题多解、一题多变、一题多用等问题,培养学生全方位、多层次探索问题的能力之外,还应设计一些开放性问题,通过寻求问题的结论或某种规律,发展学生的求异思维,培养学生的创新能力。
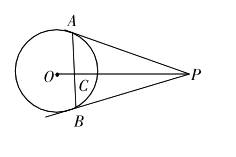
例如,教学切线长定理时,教师设计了如下问题:如图,已知PA,PB是圆O的切线,A,B为切点。AB与OP相交于C。根据已知条件,写出四个结论(多者不限)。教师可多设计一些这样的给出条件、探索结论的问题,能够使学生发散思维,有利于培养求异思维能力。
(作者单位:双峰县锁石中学)