小学数学思想方法渗透探析
赖丽华(德化县尚思小学,福建德化362500)
小学数学思想方法渗透探析
赖丽华
(德化县尚思小学,福建德化362500)
数学思想方法对于开发学生智力,培养良好的思维品质以及加强中小学数学教学的衔接都是大有裨益的。教学中,教师在传授给学生数学知识的同时,还要注重数学思想方法的渗透,提升学生的数学核心素养。
思想方法有序;转化;数形结合;数学模型
数学思想方法,是对数学知识发生过程的提炼、抽象、概括和升华,是对数学规律的理性认识,是数学教学的灵魂。数学学习,除了获得基本的知识技能,最重要的就是感悟数学中蕴含的基本数学思想。数学教学的最高境界是在传授给学生数学知识的同时,注重数学思想方法的渗透,从而提升学生的数学核心素养。
一、有序,建构知识框架
数学知识发生、形成、发展的过程,就是数学思想方法产生的过程,因此,教师不仅仅要引导学生解决数学问题,更应该把学生的思维通过数学问题引向更广阔的数学空间,去发现问题,解决问题,尝试创新,并感受数学思想方法。
如在教学《6和7的组成》时,学生汇报6的分法时,有些学生分出了3种,有的学生分出了4种,有的学生分出了5种,有的学生按一定的顺序来分,有的学生没有按顺序分。展现在教师们面前的学生的分法有点杂乱且无序,他们不容易也很难看出其中隐含什么样的规律和蕴含着什么样的数学思想。面对低年级学生的无序摆放,此时笔者就抓住学生生成资源的这一细节进行追问:“这样看起来有点乱,小朋友们,能不能想个办法让它们分得既不会重复又不会遗漏呢?”然后再给学生充分的动手、探究、发现的时间,引导探索将一个数分成两份时,如何能穷尽所有的分法,让学生自主讨论。最后进一步总结提升,引导学生观察比较出:有序和不会重复也不会遗漏包含了两种方法,一是按顺序分;二是一组一组地分。例如6分成两份有5种分法,6可以分成1和5,6可以分成2和4,6可以分成3和3……接着对7的分法,就可以采取用同样的方法放手让学生独立自主地操作,最后学生能够很快正确地汇报出7的两种分法如下,第一种方法是按顺序分(包含从小到大,和从大小的分法)。

按从小到大进行分与合,左边的数从1开始分起,然后依次增多,右边的数依次减少;第二种分法即一组一组地分:按从小从大到的顺序分的同时,以组为单位进行分与合,即在分出一种的情况下,同时交换位置。如,7可以分成1和6,同时交换位置,7可以分成6和1。按顺序一组一组地分,学生马上可以想到7可以分成2和5,7可以分成5和2;7可以分成3和4,7可以分成4和3。即左右两个数交换位置,一组一组的分,分3组,同样可以得出6种分法。
在这个知识的建构过程中培养了学生有序地、全面地思考问题的意识,渗透了有序思想、优化的数学思想方法。
二、转化,突破教学重难点
一般而言,教学重难点即是必须运用或揭示的数学思想方法之处。因此,突破重难点,就得围绕渗透数学思想方法,展开教学过程。
师:平行四边形的面积=底×高,这个公式是怎样得来的?(面对这个完全陌生的问题,学生没有头绪。)
师(迟疑了一会):能不能“转化”成已学过的图形?于是笔者即刻板书“转化”。
生1:将平行四边形转化为已经学过的长方形。
师:那么,“转化”又有什么意义呢?
生2:它将一个无法解决的问题转化成了可以解决的问题。
生3:利用旧知识解决了新问题。
这样开门见山将“能不能转化成已学过的图形?”直接抛向学生,让学生独立自由地思考。接着教师用了几何画板制作的课件,向学生动态地演示一个任意四边形,满足了一定的条件就转化为平行四边形的过程,并通过课件的动态优势,演示图形运动,并配以精确的数据测量,加深学生的印象。让每个学生通过观察、操作来得出:运用“转化”思想,从“长方形的面积=长×宽”推出“平行四边形的面积=底×高”。使学生获得对数学转化思想理解的同时,认识事物之间是普遍联系、相互转化的,进而对转化的数学思想方法积累了感性认识,促进了“三维”目标的达成。
三、数形结合,化抽象为具体
高度的抽象性,是数学思想方法的主要特点之一。教学中,教师们要遵循小学生的年龄特点、思维特征,以观察、操作、思考等数学活动为载体,把某种数学思想方法融入到具体的、实在的数学知识之中,从而达到化抽象为具体的目的。如在教学《异分母分数加减法》时,解决这样一道题:“一杯牛奶,小明第一次喝了半杯,第二次又喝了剩下的一半,就这样每次都喝了上一次剩下的一半。问小明4次一共喝了多少牛奶?”一般情况下,学生会把四次所喝的牛奶加起来,通分求出4次一共喝一杯牛奶的列式为:
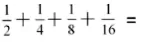
在教学中,不少学生对算理及解题过程模棱两可。这时笔者就引导学生画一个正方形表示一杯牛奶,题意如右图,让学生思考如何求,并从图中直观地得出答案。这样,从实物直观到图形直观再到数学符号,使学生感受到数形结合的思想方法在问题解决中的重要作用。

四、数学模型,拓展学生思维
教学《8的加法》的课堂巩固练习时,笔者设置了这样的情境:现在教师的一只手有5个扣子,如果再加上3个扣子,一共有几个扣子了呀?(8个)你可以用摆圆片的方式把它的算式表示出来吗?(教师指导学生摆圆片,并请一个学生上黑板进行板演摆的情况)如图:
(1)●●●●●●●●
(2)●●●●●●●●
师:这些摆法都可以用哪个算式来表示呢?
生:(齐答)5+3=8
师:那这里的5表示什么?3和8又表示什么呢?生:……
师:数学具有高度的概括性,请你们想一想,生活中5+3=8还可以表示什么呢?
生1:我有5本课外书,妈妈又给我买了3本,一共有8本课外书。
生2:我原来有5支铅笔,又买了3支,现在一共有8支铅笔。
生3:树上有5只小鸟,又飞来了3只,树上一共有8只小鸟。
生4:这本故事书我上午看了5页,下午再看3页,一共看了8页。
生5:妹妹原来有5元钱,我再给她3元钱,妹妹现在有8元钱。
……
师:孩子们,你们把意思表达得非常完整,那你们举的例子中,事情各不相同,有的是买书,有的是买铅笔,有的是讲树上的小鸟,有的讲的是看课外书,有的是讲有关钱的问题,可为什么都能用5+3=8这个算式来表示呢?
生:因为他们都是表示5个和3个合起来,一共有8个的意思,所以可以用5+3=8来表示。
师:是呀,一个算式能表示出那么多不同的事情,这算式真是太神奇、太伟大、太有意思了。
一句“请你找一找,生活中5+3=8还可以表示什么呢?”的问题,让学生通过联想进行扩展,明白生活中许多不同的情景都能用同一个算式表示的道理,从而拓展学生的思维,赋予5+3=8更多的“模型”意义,有效地渗透数学模型的思想,以此带领学生领略数学隐含的魅力。
数学思想活动无法通过短期的训练而被掌握,必须通过长期的渗透和影响才能够形成。但只要教师心中有学生,一切从学生的实际立场出发,及时捕捉,谨慎、智慧地把握并抓住教材的特点,就一定能帮助学生更好地掌握和深入理解所学的数学思想方法。因此,在进行小学数学的教学过程中,教师们应该“随风潜入夜,润物细无声”,让数学思想方法之雨滋润学生的心田。
[1]沈文选,杨清桃.数学思想领悟[M].黑龙江:哈尔滨工业大学出版,2018.
[2]史宁中.数学基本思想16讲[M].北京:北京师范大学出版社,2016.
[3]王永春.小学数学思想方法的梳理[M].北京:课程教材研究所,2014.
[4]林碧珍.构建富有数学思想的课堂[M].福州:福建教育出版社,2014.
(责任编辑:陈志华)

