一类进化分布动态模型及其应用

韩晓卓, 覃姜色, 杨淑伶,*, 惠苍

1. 广东工业大学, 应用数学学院, 广州 510520

2. Stellenbosch大学, 数学系及开普顿数学中心, Matieland 7602, 南非

一类进化分布动态模型及其应用

韩晓卓1, 覃姜色1, 杨淑伶1,*, 惠苍2

1. 广东工业大学, 应用数学学院, 广州 510520

2. Stellenbosch大学, 数学系及开普顿数学中心, Matieland 7602, 南非

文章介绍了一类用以描述由自然选择作用引起物种表型进化的动态模型。该模型通过反应扩散方程和积分微分方程表达种群内不同表型特性间可能的竞争、利用与互惠等生态作用, 进而导致可能的定向和分歧选择, 从而实现表型特征的收敛和分岔动态, 形成种内和种间的多样化。通过举例和数值模拟发现, 该模型对于解释同域物种形成和生物间相互作用对表型进化的影响具有重要的理论价值。文章进一步说明表型特征的稳定进化分布与进化稳定对策理论的一致性。

适应性动态; 进化分布; 反应扩散方程; 积分微分方程; 进化稳定对策

Key words:adaptive dynamics; evolutionary distribution; reaction-diffusion equation; integro-differential equation; evolutionarily table strategy (ESS)

1 前言

适应性进化在传统意义下被看作是有机体在静态的适合度景观上的爬坡过程和生态位充填过程。这种适应性导致的种内甚至种间多样化, 常常出现在环境梯度上或成为由地理迁移障碍而导致的局域特定表型。因此, 局部生态系统所能容纳的物种数量通常取决于生态位竞争强度和环境容纳量。相反的, 协同进化往往会引发频率或密度依赖选择, 致使一类物种的进化改变可以导致不同表型以及物种种群大小的变化, 从而胁迫另一物种的适应性反应以平衡其适合度的改变[1]。这样一个动态的适合度景观, 可以促使物种通过定向选择和分歧选择的方式达到其表型特征的收敛和分岔的状态, 进而导致种内和种间多样化进化的可能性[2]。

一般意义下, 进化轨迹被视为有机体通过优化其生活史策略(或特性)试图使其适合度最大化的进化动态过程。这一观点其实包含了两个假设: 首先,在可实现的特性集合中, 适合度测度可以最大化;其次, 通过进化改变的逐渐累加作用, 最优性状是可以达到的。由第一个假设得出进化稳定策略的定义(Evolutionarily Stable Strategy, ESS); 而第二个假设是指最优特性的收敛稳定状态: 即邻近最优特征的特性可以被更接近的特性通过定向选择而入侵、取代并替换。收敛稳定的 ESS被称为连续稳定策略Continuously Stable Strategy, CSS)。通常, 所谓的进化入侵分析(Evolutionary Invasion Analysis, EIA)就是一组定量分析方法, 旨在给出 ESS存在并可以由稀有突变特性通过入侵替换而最终达到的进化条件[3].

适应性动态方法(Adaptive Dynamics, AD)是用于研究数量特性或表型特征进化动态的一个有力的分析工具, 于1990年由博弈论学家[3–4], 种群遗传学家[5]和理论生态学家[6]发展起来, 适用于当适合度为密度依赖或频率依赖时由稀有且微小的突变所引起的进化改变[8]。当群落或种群中的个体相互作用时, 其适合度不仅取决于自身的性状, 还取决于其他不同性状个体的频率或密度。因此, 性状的演化可以通过检测处于稳定平衡的群落中稀有突变的存活率来评价。而适应性动态的典型方程就是用以描述表型特性在定向选择的作用下通过稀有突变在本地种群中的连续入侵。

然而, 上述AD模型的进化稳定分析方法, 常常忽视了进化特征的差异性, 实际上只考虑了特征均值的进化[7]。然而, 如果只针对平均特征或均一特征进行分析的话, 将忽略许多重要的生态和进化方面的问题, 从而导致例如对入侵物种传播速度的低估[9]。而且, 对于平均特征的数值分析, 还经常取决于对生态时间尺度和进化时间尺度的分离, 这一假设有悖于近来所观察到的生态与进化过程可以发生在相似时间尺度上[10]。鉴于上述原因, 根据Levin和Segel[12]于1985年提出的最初假设, Cohen[13]于2003年引入了进化分布(Evolutionary Distribution,ED)的概念, 用以研究连续特征空间上生物特征的进化动态。ED概念的发展来源于对反应扩散方程的扩展, 其中反应项用以表达如不同特征间的竞争和捕食等生态作用, 而扩散项则代表了表型特征在该特征空间上的漂变过程。随后, Cohen在2009年讨论了ED的一般性概念和在不同生态系统中的应用[14], 并于2011年先后考虑了具有时滞的ED系统[15–16], 确立了资源耗散系统进化动态所满足的条件。本文将在第二部分中, 首先介绍进化分布动态方法, 然后就其简单的应用说明结果的意义, 并就相关问题进行讨论。

2 模型

2.1 模型建立

自然选择作用下的种群动态数学模型需明确表达三项内容: 种群的增长动态、遗传变异规律和自然选择过程, 现分别作以说明。首先, 假设U(t)为t时刻时的种群密度函数, 其增长动态可利用经典生死过程表示, 即:

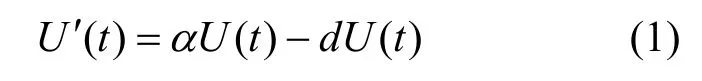
其中α代表种群的内禀增长率, 当然这里只是最简单的情形, 如果考虑α是表型特征和密度依赖时, 模型会相应的变复杂; d（U(t)）表示依赖于自身密度的种群死亡率。当考察具有某种特定特征的种群时, 可将上述密度函数定义为U(x,t), 其中x代表表型特征值。

其次, 考虑遗传变异规律以非常小的概率随机

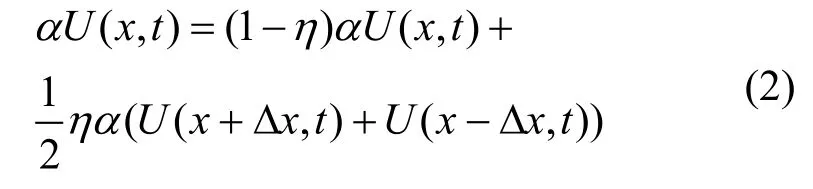
这意味着, 种群的增长过程除了自身的内禀增长项外, 还来自于相邻表型特征值的突变过程。根据泰勒级数展开定理, 上式(2)可转换为如下表达式:

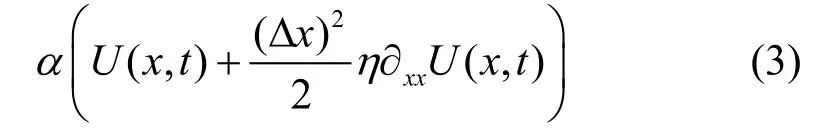
若记ε2=η(Δx)2(也可称为突变率), 则根据方程(1),表型x的进化分布动态即为:

方程(4)即为经典 Fisher反应扩散方程的扩展, 体现了具有 x特性的种群密度U(x, t)增长率随x±Δx突变作用而变化的动态。

如果突变是发生在整个连续的适应性特征区间内, 则上述动态方程需要利用积分微分方程来表达。令ζ(≥0)是定义在ℝ上的光滑函数, 满足∫ℝζ(x) dx=1。考虑到不同的表型特征可能产生的突变效果, 取突变核函数为:以表示特性x的突变概率,通常定义为任一点x到某一中心之间欧氏距离的单调函数, 即当x远离该中心时, 函数取值很小, ε代表突变核的宽度。不失一般性, 选择均值为0、方差为2ε的高斯函数作为ζ的主要形式, 即:

其中方差代表表型特征以z值为中心的突变率大小。此时, 种群生长过程可表达为:

将其带入到方程(1), 则得到如下具有突变形式的种群特征动态:

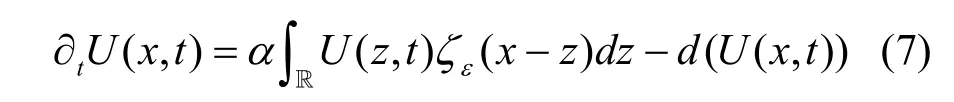
需要说明的是上述分别给出的具有离散特征值和连续特征值的突变形式的动态(即方程(4)和方程(7))只有当同时满足时间间隔很小和突变核为高斯函数两个条件时, 才具有一致的结果(具体证明过程参见参考文献[17])。

最后, 考虑自然选择过程。选择是指特征x在某个时刻 t产生具有相同特征的后代的能力相比于其他特征y(x≠y)具有明显的优势, 而且这种优势不仅取决于特征x和时间t, 也依赖于具有这种特性的种群密度U(x, t), 从而直接影响种群的增长动态。又因为不同表型间的死亡率也存在差异, 因此, 常常通过定义某一特性在某点死亡率最小来体现选择优势。将方程(4)或方程(7)中的d(U(x, t))项改写为s(U(x, t),x) U(x, t), 以此体现具有密度和特征依赖的选择效应, 其中s为自然选择函数。不同的生态过程对进化结果的影响也可在此项中表达。综合上述三个过程, 种群特性的进化动态即为如下形式:

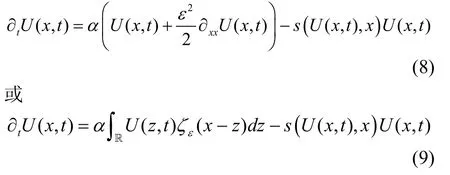
其中方程(8)中的扩散项用以表达表型适应性特征的遗传变异过程, 而反应项则表达自然选择的进化过程。

上述针对于一个适应性特征的进化动态, 可直接推广到具有n个特性的情形。Cohen和Galiano于2013年明确给出了多个特性的进化分布(ED)的定义[14]:

的解即为表型特征的进化分布。其中α和s参数意义同上, εi第i个适应性特征的突变率。此类方法还可以进一步扩展为考虑不同特征间的协同变异, 即类似于Price方程的拓展模型。

2.2 应用

生态学家曾认为: 在单个(同域)种群中发生物种分化的可能性极低, 新物种只有在异域的前提下通过物种子种群间的某些基因流障碍隔离而形成。但这一观点受到 Dieckmann和 Doebeli[18]的质疑,他们认为同域或异域都有可能导致新物种的形成。在这里, 我们通过简单的模型说明由竞争引起的自然选择作用可以导致连续特征分布上某些表型的种群密度呈现明显分化或多态状态, 从而诱发物种形成。

作为自然选择的主体, 竞争只是导致种群密度U下降, 它并不影响突变过程和种群密度的增加。由于竞争通常发生在表型特征具有较小差异的个体间, 类似的, 我们仍采用高斯函数表示种群密度因竞争而导致的减少过程:

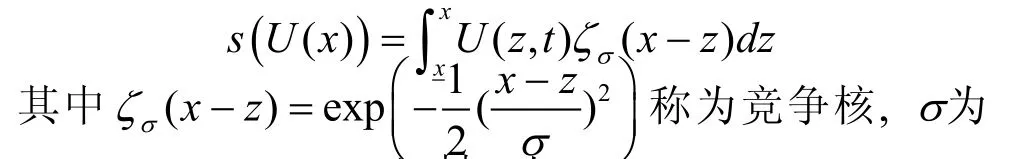
竞争核宽度, 反映表型相似特性之间的竞争强度。此时根据方程(8), 单个表型特性的进化分布动态可表达为:

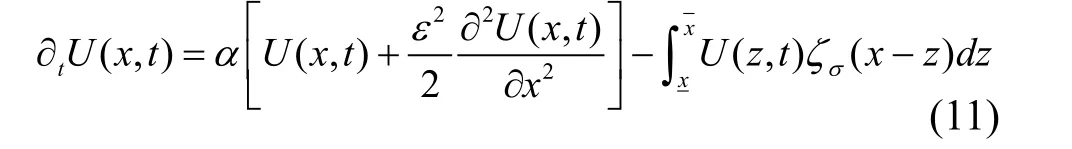
3 结果

从模拟结果看出: 随着时间的增加, 表型特征的密度分布曲线由单峰逐渐转变为双峰分布(见图1)。如果将特性密度达到局部最大值的点称为一个新的变体(morph)的话, 那么变体的数目可以量化表型的多样性。此时, 由图1可见: 原本具有唯一表型的物种则显然分化为两个子物种, 呈现出表型的多向性分布特点[14][19]。

模型中的参数σ作为竞争强度的刻画指标, 具有重要的生态学意义, 其由小到大的变化趋势反映了相似特性间由强变弱的竞争关系。该参数对于表型特性进化分布动态的影响见图 2。当σ=0.1时,单一的特征初值随时间变化扩展到整个特征区间上;当σ=0.5时, 特征最终分化为较为明显的3种变体,其中中间的特征密度相对于边界两端的密度较低;而当σ增加到1时, 中间的特征消失, 连续特征则在靠近边界的两侧形成差异较大的2种变体, 导致明显的表型隔离; 直到σ=2时, 具有高密度的初始特征也逐渐消失, 整个特征区间上并无显著的特征产生。显然, 随着参数σ值接近零时, 可以有无限表型共存,这就是所谓的极限相似性原理。根据密度值进一步可看出: 具有强竞争关系的表型特征, 相对于较弱的竞争关系而言, 在进化稳定后具有较高的种群密度。

另外, 如果将进化分布动态公式(11)中的积分符号改为正号的话, 则竞争关系转换为有利于特征增加的合作关系, 那么, 图2中σ=1的情形, 其表型特征的中间值密度将因合作关系而成为特征分布中的最大值。这意味着生态关系中, 竞争引起多样性的增加, 而合作却使多样性减少。

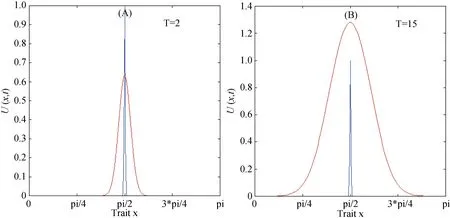
图 1 具有竞争作用的进化分布动态。蓝色线为特征初值, 红色线为特定时间步长下的进化分布。参数为:α=1,σ=1,ε2=0.005,=0,=π.Fig. 1 Dynamics of evolutionary distribution with competition. The blue lines are initial values of trait, and the red lines are evolutionary distribution at certain times steps. Parameters are α=1,σ=1,ε2=0.005,=0,=π.

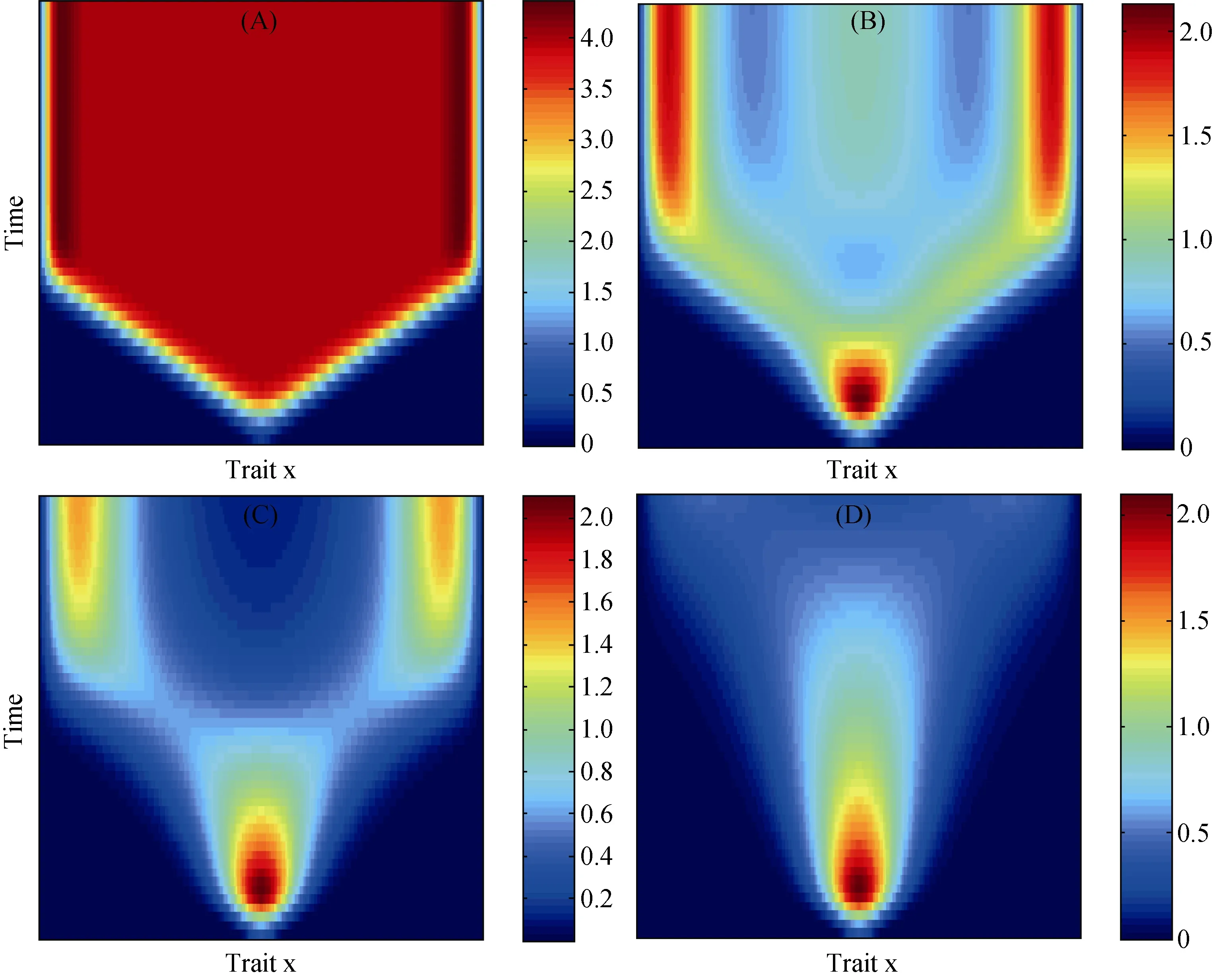
图2 参数σ对种群密度进化分布的影响, 其中(a) σ=0.2, (b) σ=0.5, (c) σ=1, (d) σ=2, 其他参数为: α=1,σ=1,ε2=0.005,=0,=π, T=50.Fig. 2 Effects of different parameter 错误！未找到引用源。 on evolutionary distribution of the traits’ density, with (a) σ=0.2,(b) σ=0.5, (c) σ=1, (d) σ=2, Other parameters are: α=1,σ=1,ε2=0.005,=0,=π, T=50.

4 讨论

之前有关进化的数学模型都是建立在适合度景观概念的基础上: 即景观的高处位置具有较高的适合度, 表型以爬坡(hill-climbing)的方式向景观高处移动, 这一动态变化过程体现了进化中的突变、变异和选择等主要过程。用适合度景观的观点把进化过程理解为有机体在具有一定特性的表型地貌上的运动过程, 其最终结果受控于因环境因素导致的选择[20]。然而, 事实上, 适合度景观的比喻忽略了进化中的另外一种动态过程: 虽然环境对选择过程、进而对有机体的适应性施加了影响, 但是后者同样可以塑造环境[21], 也即生态位构建的作用[22]。最初的适合度景观的概念并没有给予这一过程没有明确的表达。然而, 在进化分布动态的框架下, 表型不再沿着适合度景观徘徊或游荡, 后代通过其特征的局部突变过程就产生在这些表型的亚群中。因此, 进化分布框架下的表型不再是一张适合度景观图, 而是像抛一条具有固定边界(Dirichlet函数)的毯子而形成的曲面。

利用进化博弈理论研究生态与进化诸多问题的核心概念是进化稳定对策(ESS), 它是指如果占群体绝大多数的个体选择进化稳定策略, 那么, 小的突变者群体就不可能侵入到这个群体; 或者说, 在自然选择压力下, 突变者要么改变策略而选择进化稳定策略, 要么退出系统而在进化过程中消失。通常,研究进化博弈的目的旨在找到进化对策达到ESS状态时突变不可入侵的条件。目前, 为获得这一条件而广泛使用的方法即为Dieckmann[7]于1997年提出的适应性动态方程。然而, 本文所介绍的进化分布方法则具有更好的适用性。根据模型部分的介绍,ED方法研究的适应性特征具有连续性。对特定进化系统的分析表明: 局部稳定的进化分布不可能被突变的表型小种群入侵。换句话说, 动态博弈中的入侵实际上是通过稳定ED的扰动表示的; 如果ED为全局稳定, 那么相应于ESS的稳定条件则也是全局上的[14]。

然而在具体的数值计算中, 由于偏微分方程、特别是非线性系统的偏微分方程稳定性理论还不完备, 导致ED的稳定性研究也变得更为复杂。一般而言, 所有 ED模型的表型特征的初始条件都选择在资源分布的峰值处以 Dirac函数形式给定。通过数值模拟发现, 如果较前一时间步长, 系统出现了一个或两个局部最大值, 那么该最大值点在数值上就被认定为是一个分支事件, 也即新变体的出现。当然, 数值波动也可能引起特征的局部最大值, 导致假分支的出现。为了有效避免该风险, 建议每20个时间步长进行检测是否有分支出现, 进而利用平均算法将更小尺度上的波动移除。需要说明的一点是:表型是指一个有机体所表现出来的一组特殊的适应性特征值的集合。在一个种群中适当的表型差异是存在的, 对这些表型内差异, 我们不去处理。但是, 如果当这些差异达到一定的数量级, 必然受到自然选择作用的约束, 就有必要将具有较大差异的表型值认定为是不同的子种群, 从而表明多样化的产生。

目前, 关于特征进化的研究已有越来越多的用到此方法。Doebeli和Ispolatov[19]通过物种对资源竞争的进化动态说明: 如果有机体的生态属性是由复杂的多重特征所决定的话, 那么频率依赖选择对于产生多样性的条件相对于高维表型空间下多样性产生的条件更容易满足。Minoarivelo and Hui[23]利用具有依特征调节关系的双向互惠网络的生态与进化模型研究了网络连通性、嵌套性和模块化的特有水平是如何受到资源可利用性、互惠关系与竞争强度之间特性差异性的容忍度以及竞争强度等的影响。结果证实: 通过特征调节的生态与进化过程的相互作用能够解释在互惠网络中复杂的结构特点。另外,Hui[23]等人也在《Evolutionary Biology: Biodiversification from Genotype to Phenotype》书中, 用一章的篇幅介绍了AD和ED两种方法, 并就依特征调节的竞争作用、交叉营养级关系和消耗生态位宽度(食谱宽度)对协同进化系统中适应性多样性的重要性影响进行了详细的研究[24]。Landi[2]等人通过建立尺寸大小结构种群的生态进化动态模型来研究渔业政策、捕鱼死亡率、生活史妥协关系和其他统计与环境参数对分裂选择的潜在影响。

此类适应性进化模型除了可以研究上述的关于种内特征多态以及物种形成的问题[25], 还可以对很多关于特征依赖的生态学现象进行机理性的讨论。我们这里罗列两个具有研究前景的例子。第一, 入侵生物学的中心议题是关于对入侵物种入侵力和被入侵生态系统的特征表达。给定一个生态系统中物种特征的完备描述, 入侵物种的何种特征会产生最大的入侵力和影响力？这些问题同样可以用特征进化的方法予以描述和讨论[26–27]。第二, 关于生态位构建的众多研究已表明: 有机体与环境的反馈机制对物种的多样性分布结构、集合种群的时空动态和相互作用的生态系统产生深远的影响[24]。事实上,生态位构建作为改变物种进化源的一种推动力, 也将显著改变物种的进化轨迹[24]。因此, 利用进化分布模型探究有机体的生态位构建作用对物种进化动态、物种形成、多态维持机制以及进化稳定条件等方面的影响将具有重要的理论价值。

致谢：感谢英国约克大学(University of York)复杂系统分析中心(York Centre for Complex Systems Analysis, YCCSA)在访学期间提供的所有帮助。

[1] HUI C, MINOARIVELO HO, NUWAGABA S, et al.Adaptive diversification in coevolutionary systems. In: P.Pontarotti (ed.) Evolutionary Biology: Biodiversification from Genotype to Phenotype[M]. Springer, Berlin, 2015,pp.167–186.

[2] LANDI P, HUI C, DICECKMANN D. Fisheries-induced disruptive selection[J]. Journal of Theoretical Biology,2015, 365: 204–216.

[3] OTTA SP, DAY T. A biologist’s guide to mathematical modelling in ecology and evolution[M]. Princeton University Press, Princeton, 2007.

[4] NOWAK M, SIGMUND K. The evolution of stochastic strategies in the prisoner’s dilemma[J]. Acta Applicandae Mathematicae, 1999, 20: 247–265.

[5] ABRAMS PA, HARADA Y, MATSUDA H. On the relationship between quantitative genetic and ESS models[J]. Evolution, 1993, 47: 982–985.

[6] METZ J, NISBET R, GERITZ S. How should we define‘fitness’ for general ecological scenarios[J]. Trends in Ecology & Evolution, 1992, 7: 198–202.

[7] DIECKMANN U, LAW R. The dynamical theory of coevolution: a derivative from stochastic ecological processes[J]. Journal of Mathematical Biology, 1996, 34:579–612.

[8] WAXMAN D, GAVRILETS S. 20 questions on adaptive dynamics[J]. Journal of Evolutionary Biology, 2005, 18:1139–1154.

[9] RAMANANTOANINA A, OUHINOU A, HUI C. Spatial assortment of mixed propagules explains the acceleration of range expansion[J]. PLoS ONE, 2014, 9: e103409.

[10] YOSHIDA T, JONES L, ELLNER S, et al. Rapid evolution drives ecological dynamics in a predator-prey system[J].Nature, 2003, 424: 303–306.

[11] JONES LE, BECKS L, ELLNER SP, et al. Rapid contemporary evolution and clonal food web dynamics[J].Philosophical Transaction of the Royal Society London B,2009, 364: 1579–1591.

[12] LEVIN SA, SEGEL LA. Pattern generation in space and aspect[J]. SIAM Review, 1985, 27: 45–67.

[13] COHEN Y. Distributed predator-prey co-evolution[J].Evolutionary Ecology Research, 2003, 5: 819–834.

[14] COHEN Y. Evolutionary distributions[J]. Evolutionary Ecology Research, 2009, 11: 611–635.

[15] COHEN Y. Darwinian evolutionary distributions with time-delays[J]. Dynamics of Continuous, Discrete and Impulsive Systems, Series B: Applications and Algorithms,2011a, 18: 29–48.

[16] COHEN Y. Evolutionary distributions: producer consumer pattern formation[J]. Biological Dynamics, 2011b, 5:253–267.

[17] COHEN Y, GALIANO G. Evolutionary distributions and competition by ways of reaction-diffusion and by ways of convolution[J]. Bulletin of Mathematical Biology, 2013,75(12): 2305–2323.

[18] DOEBELI M, DIECKMANN U. Evolutionary branching and sympatric speciation caused by different types of ecological interactions[J]. American Naturist, 2000, 156:S77–S101.

[19] DOEBELI M, ISPOLATOV I. Complexity and diversity[J].Science, 2010, 328: 494–497.

[20] WRIGHT S. Evolution and the genetics of population[M].University of Chicago Press, Chicago, 1969.

[21] METZ J, NISBET R, GERITZ S. How should we define‘fitness’ for general ecological scenarios[J]. Trends in Ecology & Evolution, 1992, 7: 198–202.

[22] LALAND KN, ODLING-SMEE FJ, FELDMAN MW. The evolutionary consequences of niche construction: a theoretical investigation using two-locus theory[J]. Journal of Evolutional Biology, 1996, 9: 293–316.

[23] MINOARIVELO HO, HUI C. Trait-mediated interaction leads to structural emergence in mutualistic networks[J].Evolutionary Ecology, 2016, 30: 105–121.

[24] BRANNSTROM A, LOEUILLE N, LOREAU M, et al.Emergence and maintenance of biodiversity in an evolutionary food-web model[J]. Theoretical Ecology, 2011,4: 467–478.

[25] ZHANG F, HUI C, PAUW A. Adaptive divergence in Darwin’s race: how coevolution can generate trait diversity in a pollination system[J]. Evolution, 2013, 67: 548–560.

[26] HUI C, RICHARDSON DM, LANDI P, et al. Defining invasiveness and invasibility in ecological networks[J].Biological Invasions, 2016, 18: 971–983.

[27] MINOARIVELO HO, HUI C. Invading a mutualistic network: To be or not to be similar[J]. Ecology and Evolution, 2016, DOI: 10.1002/ece3.2263

[28] 莫昌健, 韩晓卓. 生态位构建作用对捕食-竞争系统的影响[J]. 生态科学, 2016, 35(5): 73-81.

[29] 崔丽娟, 李伟, 赵欣胜, 等. 采砂迹地型湿地恢复过程中优势种群生态位研究[J]. 生态科学, 2013, 32(1): 073–077.

On the dynamical model of evolutionary distribution and its application

HAN Xiaozhuo1, QIN Jiangse1, YANG Shuling1,*, HUI Cang2
1. School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China 2. Department of Mathematical Sciences, Stellenbosch University, and African Institute for Mathematical Sciences,Matieland 7602, South Africa

Adaptive dynamics of functional traits for interacting and coevolving species is the crux of ecology and evolution.We here introduce the dynamical model of evolutionary distribution (ED) that encapsulates the evolutionary dynamics of functional traits under natural selection. Such models are formulated in the form of partial differential equations of the reaction-diffusion type, using integro-differential equations to express trait-mediated ecological interactions and the diffusion trait mutation. The ED model can thus portray the adaptive dynamics of interacting traits for coevolving species under typically frequency- or density-dependent selection due to reciprocal biotic interactions such as competition, antagonism and mutualism.Traits of coevolving species can converge or diverge in the ED model, respectively, through directional and disruptive selection,resulting in a wide range of intra- and inter-specific evolutionary trajectories and possibilities, such as the Red Queen dynamics and adaptive diversification. Using a simple system with species competing for resources, we demonstrate the potential of using such models for investigating the emergence of polymorphism and sympatric speciation, as well as the effects of the types and strengths of ecological interactions on phenotypic evolution. We show that the stable evolutionary distribution of functional traits actually corresponds to the evolutionarily stable strategy (ESS) of the multiplayer evolutionary game. The ED model is,thus, a powerful tool for exploring the diverse and complex trajectories of coevolutionary systems.

10.14108/j.cnki.1008-8873.2017.03.019

Q141

A

1008-8873(2017)03-135-07

韩晓卓, 覃姜色, 杨淑伶, 等. 一类进化分布动态模型及其应用[J]. 生态科学, 2017, 36(3): 135-141.

HAN Xiaozhuo, QIN Jiangse, YANG Shuling, et al. On the dynamical model of evolutionary distribution and its application[J].Ecological Science, 2017, 36(3): 135-141.

2015-12-05;

2016-03-05

国家自然科学青年基金项目(11401115), 国家自然科学面上项目(31670391), 国家留学基金委国家公派高级研究学者及访问学者(含博士后)项目(201508440178)

韩晓卓(1978—), 女, 青海西宁人, 博士, 副教授, 主要从事数学生态学研究, E-mail: hanxzh@gdut.edu.cn; 覃姜色(1989—), 男, 广西柳州人,硕士研究生, 从事数学生态学研究, E-mail: 413922421@qq.com

*通信作者:杨淑伶(1977—), 女, 硕士, 讲师, 主要从事偏微分方程数值计算研究, E-mail: t_ysl@163.com; 惠苍(1977—), 男, 博士, 教授, 从事理论生态学与进化生态学研究, E-mail: chui@sun.ac.za