基于内点法的不敏卡尔曼滤波算法

贺姗+师昕

摘要：针对非线性不等式状态约束滤波问题，提出一种基于内点法的不敏卡尔曼滤波算法。该算法在不敏卡尔曼滤波的基础上结合了优化算法的思想，采用内点优化法求解非线性不等式约束条件下的最优解。在算法实现过程中，引入障碍项，用无约束障碍函数近似化受约束目标函数，采用一个相当小的正数即障碍因子，通过序列极小化方法逐渐减小该障碍因子，经过迭代快速搜索出非线性不等式状态约束问题的近似最优解。对具有约束的航路跟踪系统进行实验仿真，实验结果表明新算法在处理非线性不等式状态约束滤波问题时，能够有效地提高状态估计精度，获得较高的滤波精度，且时间复杂度较低。

关键词：状态约束；不敏卡尔曼滤波；优化算法；目标跟踪；信息融合

DOIDOI：10.11907/rjdk.171335

中图分类号：TP312

文献标识码：A 文章编号：1672-7800（2017）006-0040-05

0 引言

在状态估计问题中，状态向量可能受到很多因素制约。例如：船只在海上航行中会受到航路的约束，钟摆摆动过程中需要遵守机械能守恒定律。若将这些约束条件有效地施加到状态估计过程中，能够更加逼近实际状态值，获得较高的滤波精度[1-3]。因此，针对受约束条件下状态估计问题的研究具有重要意义。

近年来，人们针对等式状态约束问题进行了深入研究，并提出了很多有效的约束算法。例如：水平滑动估计算法（Moving Horizon Estimation， MHE）[4-5]、平滑约束卡尔曼滤波（Smoothly Constrained Kalman Filter， SCKF）[6]、二阶泰勒级数展开非线性约束滤波（2ord Nonlinear Constrained，2ord NC）[7]等。在实际问题中，系统状态向量也可能受到不等式约束条件的限制。然而，针对该问题的研究成果较少。2002年，Simon针对不等式约束问题提出了概率密度截断算法[8]，该算法将不等式约束函数转换为概率密度函数，能够获得较高的滤波精度，但是其计算量会随着状态维数的增大而迅速增大，因而不适合状态维数较高的约束问题。Vincent等[9]提出了一种模糊逼近的方法，即将不等式约束条件视为带有模糊噪声的量测值，然后利用拉格朗日乘子法迭代求解出受约束后下的状态估计值，然而其受限于随时间变化的约束问题。2010年，Simon[3]提出了积极集法，该方法利用先验等式约束方程对不满足不等式约束的估计值进行逼近，取得了较好效果。本文结合优化算法的思想，采用内点法[10]解决不等式状态约束滤波问题。该算法引入障碍项，将约束问题转换成无约束问题，即用障碍函数代替原目标函数，利用一个相当小的正数即障碍因子，采用序列极小化的方法，逐渐减小障碍因子，经过迭代，获得不等式约束滤波问题的近似最优解[11-13]。该算法为非线性不等式约束滤波问题提供了一种新的实现途径，并具有较好的滤波结果。

3 非线性不等式约束滤波最优解求解

经过上述UKF算法滤波后，得到滤波更新值k|k和Pk|k，此时需要通过非线性不等式约束条件对k|k进行修正，以达到约束优化的目的。为解决该非线性不等式约束问题，本文采用内点法。该算法在优化过程中引入了障碍项，用获得的障碍函数代替原目标函数，即可将复杂的约束问题转换成无约束问题。然后利用一个相当小的正数，即障碍因子，采用序列极小化的方法，逐渐减小障碍因子，迭代求解出非线性不等式约束滤波最优解。内点法在可行域周围筑起一道“障碍”，一旦搜索点接近该边界时，通过迅速增大障碍函数，迫使迭代点始终都在可行域内部。当搜索点远离可行域边界时，则用障碍函数近似目标函数，此时，可以将障碍函数的无约束最优解作为带约束目标函数的最优解。针对式（5）所考虑的优化问题，其可行域为：

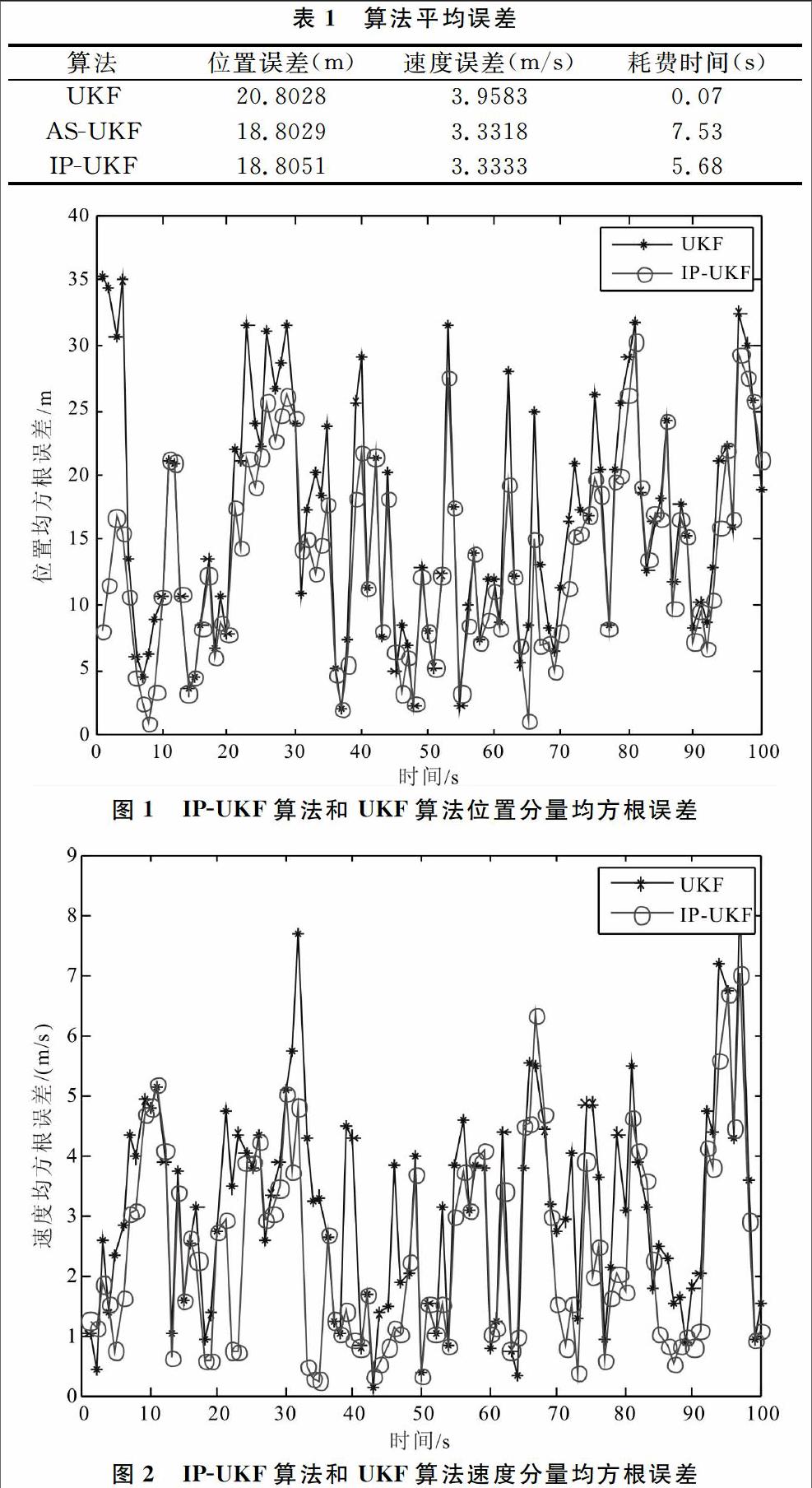
由式（41）可知该系统为非线性，滤波过程采用不敏卡尔曼滤波算法。在此基础上，通过约束式对滤波结果进行修正，以提高滤波精度。本文分别从位置均方根误差和速度均方根误差两个方面对比各算法的误差性能，实验结果如图1和图2所示。由图1可知，分别采用无约束UKF算法和IP-UKF算法对目标进行滤波后，IP-UKF算法的位置均方根误差小于无约束UKF算法的位置均方根误差，图2给出了两种滤波算法速度均方根误差的对比结果，从图中易知，经IP-UKF算法滤波后的速度均方根误差小于无约束的UKF算法。从上述两方面分析结果可知IP-UKF算法与一般的无约束UKF算法相比能够取得更高的滤波精度，滤波结果更好地收敛于真实值。尽管在个别时刻出现了波峰值，但是IP-UKF算法的整体性能和无约束UKF算法相比表现较好。图3和图4为无约束UKF算法和AS-UKF算法滤波之后的均方根误差对比结果，由图可知，经过AS-UKF算法滤波后的位置和速度均方根误差均小于无约束的UKF算法的均方根误差。

为了更加清晰比对出本文提出的IP-UKF算法和AS-UKF算法的性能优越性，采用100次蒙特卡罗仿真实验，其结果如表1所示。由表1可知，经过100次蒙特卡罗实验之后，IP-UKF算法与AS-UKF算法相比较，位置和速度均方根误差相当，而时间复杂度稍低，且IP-UKF算法实施过程根本不同于AS-UKF算法：AS-UKF算法不能直接应用于不等式状态约束估计，具体实现过程中首先需要判断滤波结果是否符合约束条件，如果满足，则不进行约束处理；否则，采用先验等式约束条件对滤波结果进行约束限制，最终得到约束后的滤波结果。且AS-UKF算法在實施过程中会经常遇到困难，其计算量会随着约束条件数的增加而呈指数增长。综上所述，本文提出的IP-UKF算法能够有效地利用约束条件对状态值进行修正，算法时间复杂度较低，为解决解决具有非线性不等式状态约束的滤波问题提出了一种新的实现途径。

5 结语

针对非线性不等式状态约束问题，本文提出了一种新的算法，即基于内点法的不敏卡尔曼滤波算法。实施过程中引入了障碍项，其特点是能够将较复杂的受约束滤波问题转化为无约束滤波问题，从而可利用最优化理论解决该问题。其具体实现是在可行域内通过迭代方法，促使障碍函数和目标函数尽可能地接近，障碍函数求得的最优解即可作为约束滤波问题的最优解。本文算法为解决该类非线性不等式状态约束滤波问题提供了一种新的实现途径，通过对系统状态向量进行约束限制，可修正状态估计值，提高状态估计精度。仿真实验结果表明，本文提出的IP-UKF算法具有较小的误差值，可以更加精确地估计出状态值，使状态估计值更好地收敛于真实状态值，有效地提高了滤波精度，是一种可行的非线性不等式约束滤波算法。

参考文献：

[1]陈金广， 李洁， 高新波. 一种迭代收缩非线性状态约束滤波算法[J]. 西安电子科技大学学报，2011， 38（1）： 104-109.

[2]JULIER S，UHLMANN J， DURRANT-WHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control， 2000， 45（3）： 477-482.

[3]SIMON D. Kalman filtering with state constraints： a survey of linear and nonlinear algorithms[J]. IET Control Theory & Applications， 2010， 4（8）： 1303-1318.

[4]MICHALSKA H， MAYNE D. Moving horizon observers and observer based control [J]. IEEE Transactions on Automatic Control， 1995， 40（6）： 995-1006.

[5]RAO C， RAWLIAGS J， LEE J. Constrained linear stateestimation—a moving horizon approach[J]. Automatica，2001， 37（10）： 1619-1628.

[6]DE GEETER J， VAN BRUSSEL H， DE SCHUTTER J. A smoothly constrained Kalman filter[J].IEEE Transactions on Pattern Analysis and Machine Intelligence， 1997， 19（10）： 1171-1177.

[7]YANG C， BLASCH E. Kalman filtering with nonlinear state constraints[J]. IEEE Transactions on Aerospace and Electronic Systems， 2009， 45（1）： 70-83.

[8]SIMON D， CHIA T. Kalman filtering with state equality constraints[J].IEEE Transactions on Aerospace and Electronic Systems， 2002， 38（1）： 128-136.

[9]VINCENT S， GHALEB H， HOUCINE C. State estimation under nonlinear state inequality constraints：a tracking application[C].16th Mediterranean Conference on Control and Automation. France： IEEE，2008：1669-1674.

[10]BRADLEY M B， JAMES V B， GIANLUIGI P. An inequality constrained nonlinear Kalman-Bucy smoother by interior pointlikelihood maximization[J].IEEE Transactions on Automatic Control，2009.

[11]BOONANS J， GILBERT J. Numerical optimization：theoretical and practical aspects[M].New York： Spring， 2000：51-65，353-368.

[12]JIANG Q， GENG G C. A reduced-space interior point method for transient stability constrained optimal power flow[J]. IEEE Transactions on Power Systems， 2010，25（3）： 1232-1240.

[13]SIMON D.Optimal state estimation[M].New Jersey：John Wiley & Sons， 2006： 218-222.

[14]JULIER S，UHLMANN J， DURRANT-WHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control，2000，45（3）：477-482.

（責任编辑：陈福时）