基于贝叶斯理论的中国近海网格化气象要素概率预报研究

宋 毅，宋晓姜，高志一，张志华，李 敏

（国家海洋环境预报中心，北京 100081）

基于贝叶斯理论的中国近海网格化气象要素概率预报研究

宋 毅，宋晓姜，高志一，张志华，李 敏

（国家海洋环境预报中心，北京 100081）

基于贝叶斯理论建立了一种基本概率预报模式，将欧洲中期天气预报中心数值模式的确定性海面风场预报转换为概率预报，并对概率化后的释用产品进行了评估与检验。对2016年3月和4月释用产品的检验结果表明，在中国近海1 425个渔区的全风速预报中，贝叶斯概率预报准确率均较高；对6级及以上大风的预报，贝叶斯概率预报的准确率也较高，且空报率低，无漏报。本文的研究成果为预报员进行业务预报具有指导性意义，同时将为进一步构建海面风场的网格化业务预报体系奠定了技术基础。

贝叶斯理论；概率预报；网格化；业务预报

1 引言

随着涉海项目日益频繁，开展海洋气象要素网格化预报成为当务之急。海洋预报要素网格化预报的主要思路是，以优质的数值预报产品及相对应的历史实况观测或再分析数据为基础数据，利用气象学和海洋学诊断、统计等客观方法输出释用后的预报数据，通过交互式、网格化预报发布平台，结合预报员经验订正方法，最终完成预报要素的网格化发布。因此，选取优质的数值预报产品和适当的释用方法，以及预报员经验订正过程构成了网格化最重要的3个环节。

目前国内外主流预报机构已经开展了一系列网格化预报工作。欧洲中期数值预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）针对温度、气压要素、风要素采用高斯密度分布对预报结果进行订正[1]，针对降水量采用逻辑回归[2]或分位数回归方法，贝叶斯平均方法[3]也被用于集合预报释用订正；美国国家环境预报中心（National Centers for Environmental Prediction，NCEP）利用再预报技术[4]、贝叶斯平均方法[3]等对集合预报进行释用订正；中国气象局国家气象中心研发了以“精细化气象要素客观预报平台（Meteorology Element Objective Forecast Interation System，MEOFIS）”为代表的集成多种数值预报产品解释应用技术的客观气象要素预报系统，初步建立了网格化、定量化的产品体系。当前，我国海洋预报机构的网格化预报技术尚未建立，现阶段主要依靠一线预报员主观判断对数值结果进行人工订正，主观影响较大且耗费大量人力，越来越无法满足现代海洋预报业务的要求。因此，建立开展网格化预报体系成为迫切需求。

由确定性预报向概率预报转变已成为当今天气预报的热点。由于数值模式输出的单一确定性预报产品，否定了客观存在的预报不确定性，据此而提供的预报信息是不完善的[5]，对预报员及使用者的指导意义有局限性。而通过概率天气预报，为预报员及使用者提供了对天气状况未来发展趋势认知状态的较完整表达，实现了对预报不确定性的定量化表达[6-8]。而将贝叶斯统计理论应用于概率预报技术成为了近年来数值预报的新趋势[3,9-11]。

本文工作着眼于目前亟待发展的我国海洋预报要素网格化技术，落脚于中国近海1 425个渔区（每个渔区范围为0.5°×0.5°），选用ECMWF T1279模式，依据贝叶斯统计理论，实现海面风的确定性预报向概率预报的转变，初步构建海洋气象要素的网格化业务预报。

2 数据及方法介绍

2.1 数据资料

本文所用的数值预报产品为ECMWF T1279模式预报，水平分辨率为0.125°×0.125°，选用2014年12月—2016年4月的逐12h预报数据进行分析，其中2014年12月—2016年2月数据用于概率预报模型建立，2016年3—4月作为预报试验的检验期。为了评估模式预报性能，使用了对应时期的ECMWF较高分辨率（0.125°）ERA-Interim再分析数据，该数据是ECMWF第三代再分析数据，使用了ECMWF的IFS（Integrated Forecast System）Cy31r2模型，其采用四维变分同化技术，结合改进的卫星数据误差校正等技术，相比前两代（ERA-15、ERA-40）再分析数据，其数据质量有所提升。考虑到中国近海浮标数量有限、卫星遥感数据则在时间、空间的不连续，本文在评估、订正网格化数值预报产品时，选用ERA-Interim再分析数据作为“观测值”。此外，为了讨论再分析数据的可靠性，本文还使用了2014年的中国近海22个逐小时浮标数据进行对比分析。

2.2 贝叶斯方法

贝叶斯方法描述的是两个事件的条件概率之间的关系。条件概率通常写为P(A|B)，表示在事件B发生的条件下事件A发生的概率。贝叶斯方法用公式表示如下：

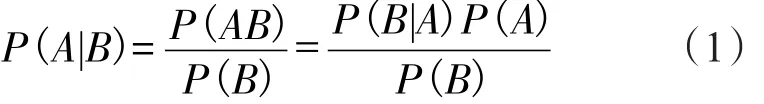
式（1）即为贝叶斯公式的密度函数形式，其中P（AB）表示事件A与B（在本文中为实况与预报）的联合概率密度函数；P（A）是事件A的边缘或先验概率分布函数，包括了A的先验信息；P（B|A）表示在事件A发生的条件下B发生的概率密度函数；P（B）是事件B的边缘或先验概率分布函数；P（A|B）称为A的后验概率分布函数。

在本文中，基于确定性预报值与观测值之间的统计关系，借助于贝叶斯统计理论，在已知预报因子的预报值情况下，获得预报量后验概率分布，把一个确定性预报转化为一个概率预报，从而实现对预报不确定性的定量化。

2.3 预报结果检验与评估

为了检验预报场与观测场之间的差异，引入模式技巧评分公式（见式（2））[12-14]

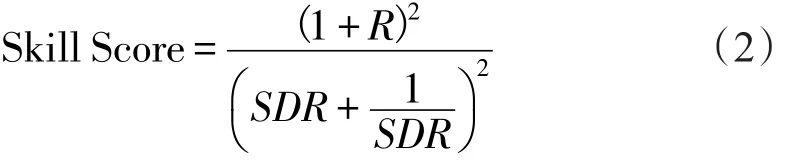
式中：R是某一区域上数值预报与观测数据时间序列相关系数；SDR是某一区域上数值预报与观测数据标准偏差的比值。上述公式综合检验了数值预报与观测数据的时间演变规律及预报偏差。根据经验，将模式技巧评分划分为5档，优秀（0.9≤S＜1）、良好（0.8≤S＜0.9）、中等（0.7≤S＜0.8）、及格（0.6≤S＜0.7）和较差（0≤S＜0.6）。

在对概率预报进行检验时，将实测风速值与检验时段下的概率预报风速区间对比。相同时刻实测风速值落在该概率预报区间内称为“准确预报”，小于该区间最低风速值称为“空报”，大于该区间最高风速值为称为“漏报”。按下列公式量化预报质量：

预报准确率（CS）：

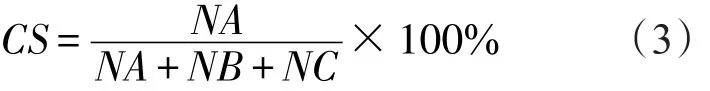
空报率（FAR）：

漏报率（PO）：

式中：NA为预报时段准确预报次数；NB为空报次数；NC为漏报次数。在本文中对全风速概率预报的检验只关注预报准确率，对大风过程预报检验则同时关注预报准确率、空报率及漏报率。

3 结果

3.1 ECMWF数值模式性能评估

在应用贝叶斯理论之前，首先对ECMWF确定性（单一）预报产品性能进行了客观检验，本文基于ERA-Interim再分析风场数据，评估了2014年12月—2016年2月ECMWF确定性预报风场在预报时效分别为24h（见图1a）、48h（见图1b）和72h（见图1c）的预报性能。如图1所示，24 h预报时效下，数值模式对黄海、东海中北部、台湾海峡、南海、日本海及西北太平洋远海的预报能力均较强，为优秀档次；对渤海、东海南部及北部湾的预报能力次之，为良好档次；中国近海沿岸、菲律宾沿岸、日本沿岸及赤道西太平洋以中等偏上水平为主，但对个别沿岸地区的预报则相对较差。

相比24 h预报时效下模式预报能力，48 h预报能力有略微降低（见图1b），主要表现在东海中北部、日本海及西北太平洋远海的预报能力由优秀档次降到良好；中国近岸预报能力仍以中等偏上水平为主。72 h的预报能力则有明显降低（见图1c），但整体仍维持在中等以上水平，仅在个别华南沿岸、台湾岛西南沿岸、日本沿岸及菲律宾沿岸的预报相对较差。

3.2 贝叶斯概率预报实例

3.2.1 贝叶斯概率预报模型

基于贝叶斯理论，对中国近海1 425个渔区逐一进行处理，同时给出订正后的最优值及概率预报区间，完善预报信息。考虑到统计订正方法需要大量样本作为基础，订正海域出现十级及以上风力事件偏少，因此本文只订正风速≤25 m/s的过程；此外，依据2014年12月—2016年2月的再分析数据与预报数据建立的库文件，当样本库中某一区间样本数占总时次的比重低于5%时，也不对该预报值进行订正，释用方法不推荐。

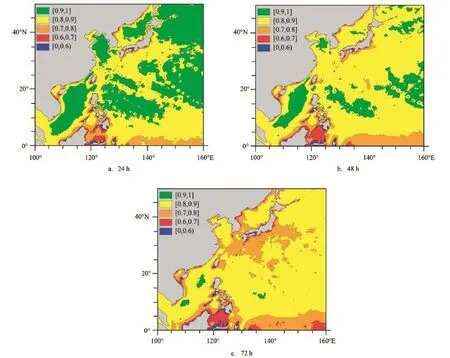
图1 西北太平洋不同预报时效下ECMWF模式海面风速技巧评分结果

图2给出了本文所用的简化贝叶斯概率预报模型流程图。以283号渔区（位于台湾海峡，24°～24.5°N，118.5°～119°E）24 h预报时效为例，详细介绍简化贝叶斯概率预报模型的建立。如图3a，在283号渔区，再分析数据与模式预报值具有显著的线性关系，二者的联合概率密度函数分布见图3b。以预报值11.1 m/s为例，基于图3b中的联合概率密度分布，图3c中给出了在该预报值范围内再分析场数据出现的可能分布概率及对应的发生次数，当预报值为11.1 m/s时，再分析数据出现最大概率的确定预报为9 m/s，共出现次数为173次，我们将该最大概率的确定性预报值作为最优订正值。将该方法推广到25 m/s界限以内所有可能的预报值中，从而建立预报值与最优订正值之间一一对应关系（见图3d）。此外，为了实现将确定性预报转换为概率预报，通过设定某一出现概率阈值，从最大出现次数开始，依次累加，计算出现概率，当超过某一设定阈值时，得到概率预报的左右边界值，随后引入蒲氏风级表，同时结合预报员经验预报规律，将左右边界值转为风力等级。根据经验累积，在本文中概率阈值取60%，通过这种方式，将确定性预报转化为概率预报，从而更加符合预报员及用户的需求。3.2.2 贝叶斯概率预报产品

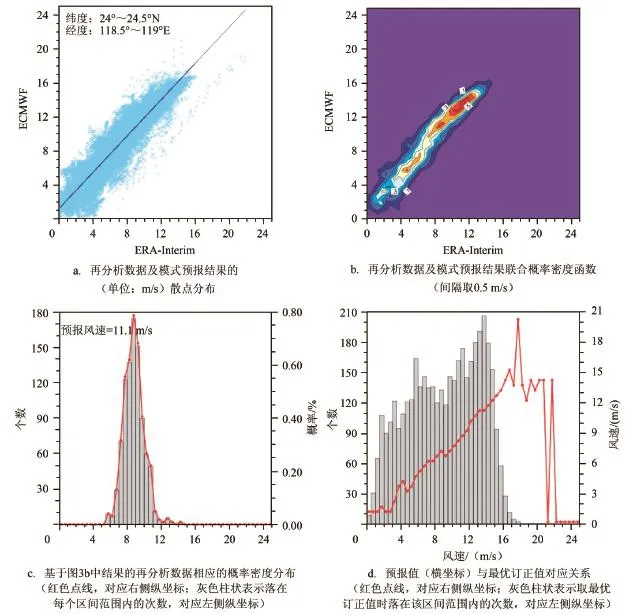
图3 283号渔区24 h预报产品订正过程

通过本文分析，最终呈现给一线预报员及用户的释用产品包括以下一些要素：ECMWF确定性预报，ECMWF模式评分，最优订正预报，概率区间预报，概率预报等级。其中，ECMWF确定性预报指ECMWF精细化预报在该渔区内的最大风速；ECMWF模式评分分为5个档次，见第2.3节预报结果检验与评估；最优订正值是通过概率预报得到的最优确定性预报；概率区间预报给出了概率阈值超过60%的预报区间；根据概率预报区间的大小，来定义概率预报等级，划分为5个档次，一档（interval≤1.0 m/s)、二档（1.0 m/s＜interval≤1.5 m/s）、三档（1.5 m/s＜interval≤2.0 m/s）、四档（interval＞2.0 m/s）和五档（当模式预报值超出概率预报释用的极大风速，如25 m/s，或者当样本库中该样本数占总时次的比重低于5%时，概率预报释用方法失效，归为此档；在此情况下，最优订正值和概率区间预报用缺测值－99.99表示）。

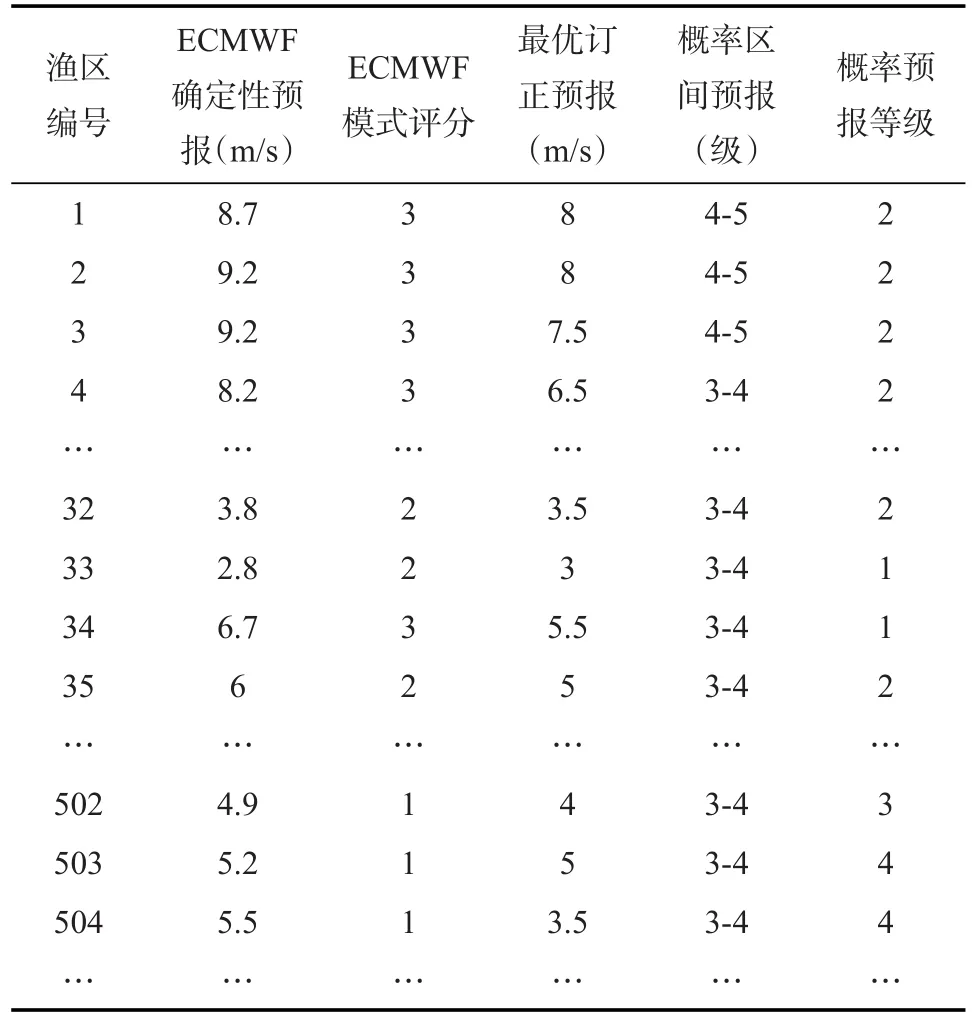
表1 最终产品示例（2016年6月19日12UTC的24 h预报）

以2016年6月19日12UTC的24 h预报时效为示例，表1给出了本文最终释用产品。为进一步完善预报产品，图4中分别给出了2016年6月19日12UTC的24 h预报示例中ECMWF模式预报评分（见图4a）和概率预报等级（见图4b）的统计结果，ECMWF模式预报结果约78.8%的渔区处于良好及优秀档次，约16.6%的渔区处于中等和及格档次，仅有约4.6%的渔区预报较差。概率预报等级统计结果显示，约83.6%的渔区概率预报区间间隔低于1.5 m/s，仅有约3.9%的渔区概率预报区间间隔高于2.0 m/s。

3.2.3 概率预报产品结果检验

采用上述产品释用方法，进行准业务化运行，目前积累了两个月（2016年3月和4月）的释用产品，将同期再分析数据视为观测数据，通过计算预报准确率、空报率和漏报率来对概率预报产品结果进行检验。对全风速24 h、48 h及72 h预报准确率的统计如图5所示，在中国近海大部分渔区，24 h及48 h预报准确率可以达到90%以上，72 h预报准确率达到80%以上；在东海东部及台湾岛以东部分渔区，预报准确率相对较低。考虑到海上渔船较为关注的是大风与大浪过程，只关注6级及以上大风过程，再次对大风概率预报进行检验。如图6所示，24 h预报时效下，近海大部分渔区的大风预报准确率也能达到90%以上，且空报率低于10%，无漏报，说明该概率预报产品具有一定的可参考性，对预报员业务工作具有一定指导意义。

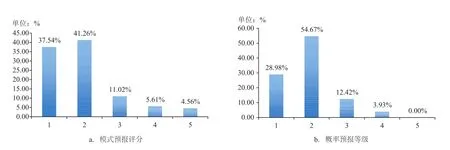
图4 产品统计结果示例（2016年6月19日12UTC的24 h预报）

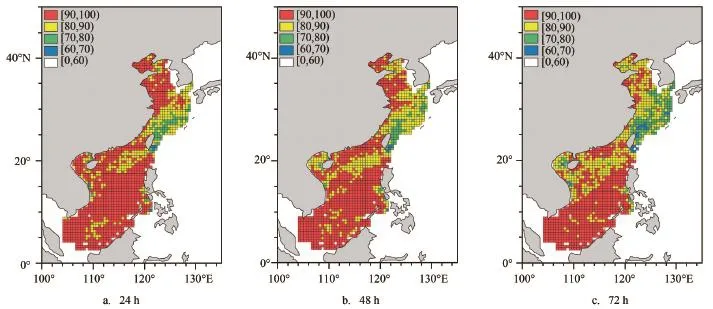
图5 2016年3—4月的释用产品中，全风速概率预报在不同时效下的预报准确率（单位：%）

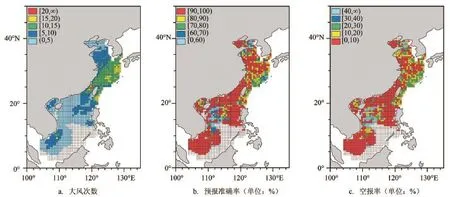
图6 2016年3—4月的释用产品中，大风（6级及以上）概率预报在24 h时效下的预报产品

另外，我们也检验了释用产品中最优订正值较ECMWF原始预报产品的优劣。图7a给出了全风速的精度检验结果，最优订正值改进效果不明显，1 425个渔区24 h最优订正值评分与模式结果评分相比基本在正负0.05之间，这与订正前ECMWF模式对全风速的预报性能已经较好有关（见图1a）。同样地将小风速过程剔除后，做风速≥5.5 m/s（4级及以上）的精度检验（见图7b），24 h预报时效下，在巴士海峡、南海东北部及北部湾的预报性能提高较为明显，模式评分增值超过0.1；48 h、72 h预报时效均有类似的特征（图略），表明该释用方法对预报性能具有一定的改善效果。

图7 24 h海面风最优订正值预报评分与ECMWF预报评分的差异

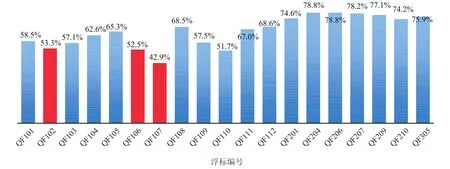
图8 基于中国近海浮标对ERA-Interim再分析风场数据的检验

4 结论与讨论

4.1 结论

基于贝叶斯统计理论，本文把ECMWF数值模式的单一确定性风场预报转化为概率预报，并实现准业务化试运行，为初步构建海洋风场网格化业务预报体系奠定基础。通过对释用产品结果的检验，得到如下结论：

（1）在对转换后的概率预报释用中，其既可作为确定性预报对外发布，也可以概率形式对外发布。因此，贝叶斯概率预报能够提供更为全面、更高精度的预报，也更加符合预报员及用户的需求；

（2）对概率预报释用产品的检验表明，对全风速预报，贝叶斯概率预报准确率均较高，可以达到90%以上。对6级及以上大风的预报，贝叶斯概率预报的准确率也较高，且空报率低，无漏报；

（3）对释用产品中最优订正值的精度检验表明，对4级及以上风速的精度预报，在部分渔区预报性能较ECMWF的确定性预报略有改善。

4.2 讨论

本文工作是面向中国近海1 425个渔区，考虑到其覆盖范围广，时空分辨率高的特点，本文选用精度较高的再分析数据ERA-Interim作为观测值进行分析。那么，再分析数据的质量则备受关注。通过对比2014年中国近海22个浮标数据，发现（见图8），再分析数据对离岸风场的刻画效果相对较好，技巧评分维持在及格及中等档次，但对近岸风场的刻画整体较差。因此，在后期工作中有必要基于再分析数据，采用合适的方法融合浮标及卫星数据，提高“观测值”的精度。

考虑到业务预报的时效性、稳定性等需求，本文选用了简化的贝叶斯统计理论来实现单一预报向概率预报的转化。后期仍需不断调研国内外最新概率预报方法，改进目前的概率预报方法，完善网格化业务预报平台。

目前，释用产品结果累积年月较少，得出相对稳定和可靠的检验结论仍需要后期进一步系统测试。

[1]Gneiting T,Raftery A E,Westveld III A H,et al.Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation[J].Monthly Weather Review, 2005,133(5):1098-1118.

[2]Wilks D S.Extending logistic regression to provide full-probabilitydistribution MOS forecasts[J].Meteorological Applications,2009, 16(3):361-368.

[3]Raftery A E,Gneiting T,Balabdaoui F,et al.Using Bayesian model averaging to calibrate forecast ensembles[J].Monthly Weather Review,2005,133(5):1155-1174.

[4]Hamill T M,Whitaker J S.Probabilistic quantitative precipitation forecasts based on reforecast analogs:Theory and application[J]. Monthly Weather Review,2006,134(11):3209-3229.

[5]周秀骥.大气随机动力学与可预报性[J].气象学报,2005,63(5): 806-811.

[6]Kelly K S,Krzysztofowicz R.Bayesian revision of an arbitrary prior density[C]//Proceedings of the Section on Bayesian Statistical Science.Alexandria:American Statistical Association,1995:50-53.

[7]Kelly K S,Krzysztofowicz R.A bivariate meta-Gaussian density for use in hydrology[J].Stochastic Hydrology and hydraulics, 1997,11(1):17-31.

[8]俞小鼎,张艺萍.天气预报技巧和价值的关系[J].气象科技, 2004,32(6):393-398.

[9]陈朝平,冯汉中,陈静.基于贝叶斯方法的四川暴雨集合概率预报产品释用[J].气象,2010,36(5):32-39.

[10]陈法敬,矫梅燕,陈静.亚高斯贝叶斯预报处理器及其初步试验[J].气象学报,2011,69(5):872-882.

[11]Herr H D,Krzysztofowicz R.Generic probability distribution of rainfall in space:The bivariate model[J].Journal of Hydrology, 2005,306(1-4):234-263.

[12]Taylor K E.Summarizing multiple aspects of model performance in asingle diagram[J].JournalofGeophysicalResearch: Atmospheres,2001,106(D7):7183-7192.

[13]Hirota N,Takayabu Y N,Watanabe M,et al.Precipitation reproducibility over tropical oceans and its relationship to the double ITCZ problem in CMIP3 and MIROC5 climate models[J]. Journal of Climate,2011,24(18):4859-4873.

[14]Chen L,Yu Y Q,Sun D Z.Cloud and water vapor feedbacks to the El Niño warming:Are they still biased in CMIP5 models?[J]. Journal of Climate,2013,26(14):4947-4961.

Probabilistic forecast of gridding 10 meter wind over China sea based on Bayesian theory

SONG Yi，SONG Xiao-jiang，GAO Zhi-yi，ZHANG Zhi-hua，LI Min

（National Marine Environmental Forecasting Center,Beijing 100081 China）

Based on Bayesian theory,a basic model of the probabilistic forecast was established out of the deterministic forecast of European Centre of Medium-Range Weather Forecast（ECMWF）.The probability forecast from March to April 2016 was evaluated by using ERA-Interim.The results show that the probability forecasts of both all wind and strong wind have better forecast values over China sea.This study not only provides a guidance forecast for forecaster and user,but also lays the foundation for building gridding operational forecast system of 10 meter wind over China sea.

Bayesian theory；probabilistic forecast；gridding；operational forecast

P732

A

1003-0239（2017）03-0001-09

10.11737/j.issn.1003-0239.2017.03.001

2016-08-15；

2016-10-24。

国家自然科学基金青年基金（41606033）。

宋毅（1988-），男，工程师，博士，主要从事海洋天气预报及年代际气候变率研究。E-mail:songy@mail.iap.ac.cn