不完整复制信号在雷达中的检测性能

杨立明，韦 高，蔚建利

(1.西北工业大学电子信息学院，陕西 西安 710072；2.西北工业大学航天学院，陕西 西安 710072)

不完整复制信号在雷达中的检测性能

杨立明1，韦 高1，蔚建利2

(1.西北工业大学电子信息学院，陕西 西安 710072；2.西北工业大学航天学院，陕西 西安 710072)

针对缺少不完整复制信号在雷达接收机上的检测性能的研究，提出了对不完整复制信号在雷达中的检测性能进行分析的方法。该方法对不完整复制的常规信号和LFM信号进行了建模，分析了上述信号在雷达中的检测性能，为客观评估该类信号在雷达中产生的干扰效果提供了理论依据。仿真验证表明，两种不完整复制的信号都可以在雷达中被检测，在适当的复制长度和信噪比条件下，不完整复制信号可以获得和原信号十分接近的发现概率。

不完整复制信号；LFM信号；检测性能；干扰效果

0 引言

现代电子战技术中，通过复制信号的一部分(为方便，本文简称为“不完整复制信号”)进行转发，转发信号被雷达接收时能够获得部分处理增益，进而产生影响雷达正常接收的假目标信号[1]。假目标信号用于干扰时使用灵活，效果明显，对雷达的正常接收产生了明显的影响。

国外针对该类信号主要开展了形成干扰的机理研究[1]，但未见针对该类信号的检测性能研究的文献。在国内，对此类信号形成的假目标干扰的效果比如功率损失、信噪比损失进行了研究[2]，对与此相关的脉内叠加信号的性能进行了分析[3]，还提出了部分拓展的干扰方法[4-5]，另外，在抗干扰方面也进行了一定的研究[6]。

但是，目前的研究尚未涉及到不完整复制信号在雷达接收机上的检测性能，本文主要针对不完整复制信号的特点，分析了该信号通过雷达匹配滤波后的变化特征，研究了该信号在雷达中的检测性能，从而为客观评估该类信号产生的干扰效果提供了理论依据。

1 不完整复制雷达信号模型

1.1 常规信号模型

为了分析不完整复制常规信号在雷达中的检测性能，需要对不完整复制常规信号建模，并分析其在通过原常规信号(这里指完整的常规信号)匹配滤波后的检测性能。

(1)

(2)

式中，ΔT为复制时间长度，通常ΔT≤T。

1.2LFM信号模型

雷达的发射信号一般可以表示为：

v(t)=u(t)ej2πf0t

(3)

现代雷达为了实现探测距离和分辨率的同时实现，大多采用了脉冲压缩技术。脉冲压缩技术的实现可以分为线性调频和相位编码，下面的分析以线性调频脉冲压缩技术为例。采用线性调频脉冲压缩技术的雷达发射信号可以写为[7]：

(4)

(5)

式中，f1=f0+μ(τ/2+τs)为不完整复制LFM信号的中心频率。

2 不完整复制雷达信号检测性能

2.1 不完整复制常规信号检测性能分析

不完整复制常规信号被接收后，首先要经过原常规信号的匹配滤波器处理，原常规信号的匹配滤波器脉冲响应满足[7]

(6)

t0是滤波器的延迟时间。则不完整复制常规信号通过原信号的匹配滤波器后的输出为:

(7)

令t-t0=t′，则

(8)

当0≪t′≪T时，

(9)

当t′=0，即t=t0时，式(9)输出值最大，

(10)

式(9)积分部分是原常规信号与其共轭信号的乘积，代表原信号的模平方。由于原常规信号已知，所以其模平方可以认为是已知的常量，设为M。

则式(9)可以简化为：

(11)

经过同样的计算过程可知，-T≪t′≪0，式(8)的输出与式(10)相同。

则在t=t0时不完整复制常规信号经过原常规信号的匹配滤波器后输出的最大信噪比可以表示为：

(12)

在ΔT=T时，相当于原常规信号经过匹配滤波器，则经过匹配滤波后的输出信噪比可以表示为：

(13)

回波信号可以看成是幅度和相位均随机变化的，在此情况下，发现概率和虚警概率存在如下关系[8]：

(14)

将式(12)、式(13)分别代入式(14)即可得到雷达对不完整复制常规信号和原常规信号的发现概率分别为：

(15)

(16)

2.2 不完整复制LFM信号检测性能分析

2.2.1 不完整复制LFM信号的匹配滤波特性

为分析方便，把复制LFM信号的矩形脉冲的中心作为时间原点，则影响不完整复制LFM信号匹配滤波特性的因素仅有复制长度。此时，f1=f0，进而可以推算出τs=-τ/2，式(5)可以改写为：

(17)

不完整复制LFM信号之所以能有效干扰雷达，是因为该信号经过原发射信号的匹配滤波器后，可以获得与原发射信号相近的处理增益。根据匹配滤波理论，信号S(t)的匹配滤波器频率特性可以写为[7]：

(18)

f表示频率。雷达发射信号S(t)通过该滤波器后的输出为[4]：

(19)

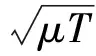
而式(17)所示的不完整复制LFM信号经过同样的匹配滤波器后的输出为：

(20)

式中，B′=μτ为不完整复制LFM信号的带宽。由式(20)可以看出，不完整复制LFM信号经过雷达发射信号的匹配滤波器后，输出的信号包络仍近似为sinc函数，但是幅度和主瓣宽度都发生了变化。

幅度变化：

(21)

主瓣宽度变化：

(22)

可以看出，不完整复制LFM的匹配滤波输出幅度降为雷达发射信号的匹配滤波器输出幅度的1/K0，而主瓣宽度则展宽到原来的K0倍。

取雷达发射LFM信号的带宽为30MHz，时宽为10μs，不完整复制LFM长度为2.5μs。这两个信号经过同一个匹配滤波器后的输出波形如图1所示。

由图1中可以看出，不完整复制LFM信号在原匹配滤波器中会有失配损失，如果考虑加窗、信噪比等损失[2]，不完整复制LFM信号的损失可达33dB。但是，干扰信号比目标回波信号具有传播路径的优势，而且干扰机功率一般能满足在雷达接收机处的功率比回波大12～13dB。因此，在不完整复制LFM干扰信号作用下，大部分干扰信号可以通过匹配滤波器而进入雷达接收机，完全可以用于对雷达实施干扰，造成对雷达检测的影响。

2.2.2 不完整复制LFM信号对雷达检测性能的影响

不完整复制LFM信号被雷达接收时，该信号和回波信号同时被检测器从噪声中检测。不完整复制LFM信号的存在会影响到回波信号的检测，这是因为不完整复制LFM信号能够获得雷达接收机的处理增益，在雷达显示器上形成密集假目标，使得操作员对目标的识别判断困难。首先分析只存在一个不完整复制LFM信号的情况，此时雷达接收信号模型可以写为：

0≤t

(23)

(24)

(25)

a1为干扰信号的复幅度，也是随机变量，设其相位分布与a0相同。由式(21)可知，雷达信号和不完整复制LFM信号通过匹配滤波器后的幅度比K0=T/τ，则不完整复制LFM信号的幅度分布密度函数可以写为：

(26)

Neyman-Pearson准则下，对目标回波的最优检测器为似然比检测器，其检测统计过程为[6]

(27)

在该检测过程中，经过包线检波后的采样时刻t0是指匹配滤波器输出信号噪声比达到最大值的时刻，对一个物理可实现的系统而言，该时刻是指在输入信号全部结束后[7]。

设LFM信号调频带宽为100 MHz，信号时长100 μs。干扰信号是原信号的20 μs重复复制形成的，干扰信号时延为1 μs。干信比为20 dB时，LFM信号和不完整复制信号经过匹配滤波和包络检波后的输出波形如图2、图3所示。

该检测过程的门限由下式确定[8]

(28)

式中Pf为虚警概率，Pf设为固定值。此时的发现概率可以根据下式得到[8]

(29)

(30)

当信号幅度服从式(25)所示的分布密度函数的瑞利分布时，回波信号的统计平均能量为：

(31)

同理，可以计算出由式(5)给出的不完整复制LFM信号的能量为：

(32)

不完整复制LFM信号被雷达接收时，其幅度经历了和回波信号相同的传播过程，可以认为其幅度也服从瑞利分布，则可以计算出不完整复制LFM信号的统计平均能量为：

(33)

(34)

将式(21)、式(32)、式(33)代入式(34)可得

(35)

为了计算方便，假设噪声功率谱密度N0=1，回波信号脉冲宽度100 μs。计算不同复制长度时的发现概率随比值k的变化情况如图4所示。

由图4中可以看出，复制长度越短，雷达检测器对干扰信号的发现概率就越小，反应在图中曲线上就是k值的增大。反之，复制长度越长，k值越小，干扰信号被检测到的概率就越大。在相同复制长度时，虚警概率越低，k值越大。这也符合实际情况，在雷达检测中，Neyman-Pearson准则以虚警概率来设置检测门限，虚警概率低，相当于检测门限高。在同样复制长度时，干扰信号获取匹配滤波的处理增益相同，门限抬高后，对应的检测概率自然降低。

雷达发射的LFM信号通过上述过程后，可以得到匹配滤波的全部处理增益，在经过包线检波，采样和门限判定后，可以被有效检测。

由于回波信号受目标反射特性和电波传播的影响，回波信号可以看成是幅度和相位均随机变化的，在此情况下，发现概率和虚警概率的关系如式(29)所示。

(36)

(37)

3 仿真验证

3.1 部分复制常规信号的检测性能仿真

设原常规信号时长为20μs，虚警概率为10-6，噪声功率谱密度变化范围为0.02～2μW/Hz。在信号时长和复制长度一定时，对应的信号功率和复制信号的功率也就确定，由式(12)和式(13)可知，噪声功率谱密度的变化对应的即为信噪比的变化。不完整复制信号的长度以占原信号时长的比例k=ΔT/T表示，取值范围为0.1～1。

计算雷达对不同复制长度的不完整复制常规信号的发现概率在不同噪声功率谱密度下的变化趋势如图5所示。

从图5可以看出，不完整复制常规信号在雷达中的发现概率与复制长度密切相关。复制长度为原信号时长0.1倍的信号要达到与原常规信号相同的发现概率(以Pd=0.3为例)，噪声功率谱密度相差可达2倍。换言之，在达到0.3的发现概率时，原常规信号可以在1.8 μW/Hz噪声功率谱密度水平下被发现，而复制长度为原常规信号时长0.1倍的信号则只能在0.9 μW/Hz的噪声功率谱密度水平下被发现。随着噪声功率谱密度的减小，雷达对不完整复制常规信号的发现概率逐渐与对原常规信号的发现概率接近。这与实际情况也吻合，因为噪声功率谱密度减小，无论对复制信号还是原信号，匹配滤波器的输出信噪比都会增大，信噪比增大到一定程度时，由式(14)可知，雷达对复制常规信号和原常规信号的发现概率将趋于相当。

3.2 部分复制LFM信号的检测性能仿真

设线性调频信号中心频率1 GHz，带宽30 MHz，脉宽20 μs；噪声功率谱0.02～2 μW/Hz。回波信号与不完整复制LFM信号的幅度均服从均值为1，方差为1的瑞利分布。计算雷达对不同复制长度的不完整复制LFM信号的发现概率如图6所示。其中，复制长度以占信号时长的比例表示，比例系数记为k，取值范围为0.1～1。

从图6可以看出，与常规信号类似，不完整复制LFM信号在雷达中的发现概率与截取长度密切相关。复制长度为原信号时长0.1倍的信号要达到与原信号相同的发现概率(设Pd=0.55)，噪声功率谱密度相差可达2倍。换言之，在达到0.55的发现概率时，原信号可以在0.8 μW/Hz噪声功率谱密度水平下被发现，而截取长度为原信号时长0.1倍的信号则只能在0.4 μW/Hz的噪声功率谱密度水平下被发现。随着噪声功率谱密度的减小，雷达对不完整复制信号的发现概率逐渐与对原信号的发现概率接近。总体上，不完整复制的LFM信号在雷达中的检测性能变化趋势与第一节分析的情况基本相同，证明了分析结果的合理性。

(38)

(39)

式(39)说明，不完整复制LFM信号经过不断转发后，输出为相互间隔为τ/2的近似目标回波信号，该信号的幅度和主瓣宽度相对于原发射信号通过匹配滤波器器的比值仍可以用式(21)、式(22)表示。由于复制信号的长度远小于发射信号，通过重复发射截取信号，可以在雷达显示器上形成比直接转发整个LFM信号密集的多的近似回波信号，造成雷达检测目标困难。

由式(32)可知，在存在部分复制LFM信号时，其被雷达检测到的概率与原信号的发现概率呈一定的比例关系。这主要是因为不完整复制LFM信号的截取长度限制了匹配滤波器后的输出，在实际使用中，有意发射的不完整复制信号相对于目标回波的路径少一倍，带来的功率损失以1/R2衰减，R为不完整复制信号发射机与离雷达的距离。而回波信号功率按原信号的1/R4衰减，回波信号比不完整复制信号的衰减要大得多。因此，在雷达接收的信号中，不完整复制信号要比回波信号强很多，相应的被发现的概率也大大增加。设雷达检测器对不完整复制信号和回波信号的发现概率相同，回波信号的发现概率降为原来的1/N，则雷达检测器对目标的检测性能将急剧恶化。设存在5个不完整复制信号，虚警概率为10-11，雷达对某个目标的发现概率曲线和存在干扰时发现概率曲线的对比如图7所示，可见雷达对目标的发现概率下降十分严重，几乎不能有效发现目标，实际使用中，不完整复制信号密集程度更高，雷达的对目标的检测性能下降严重，必须采取有效措施。

4 结论

本文提出了不完整复制信号在雷达中的检测性能的分析方法。该方法建立了不完整复制常规信号和LFM信号的模型，分别分析了两种信号在雷达中的检测性能。仿真验证表明，两种不完整复制的信号都可以在雷达中被检测，在适当的复制长度和信噪比条件下，不完整复制信号可以获得和原信号十分接近的发现概率。在多次进行复制后，可以形成可观的干扰效果。不完整复制信号极大地影响了雷达对目标的检测，必须采取措施，及时消除不完整复制对雷达的影响，保证对目标的检测性能。

[1]施莱赫D C.信息时代的电子战[M].成都：信息产业部电子第二十九研究所，2000.

[2]李宏，郑光勇，杨英科，等.部分截取雷达信号多假目标干扰性能分析[J].电子信息对抗技术，2010(3):39-44.

[3]舒玉贵，林选锋，郭燕.脉内叠加信号性能分析[J].电子信息对抗技术，2010(2)：64-68.

[4]劳国超，叶伟，阮航.基于压缩感知的LFM雷达转发干扰方法[J].电子信息对抗技术，2013(6)：40-44.

[5]潘小义，王伟，冯德军，等.基于全脉冲分段转发的LFM雷达干扰方法[J].国防科技大学学报，2013(3)：119-125.

[6]粘朋雷,李国林，路翠华，等.一种线性调频引信抗卷积调制干扰处理方法[J].电讯技术，2013(8)：1028-1032.

[7]林茂庸，柯有安.雷达信号理论[M].北京：国防工业出版社，1984.

[8]齐国清.信号检测与估计-原理及应用[M].北京：电子工业出版社，2010.

Radar Detection Performance of Partly Copied Signal

YANG Liming1, WEI Gao1, WEI Jianli2

(1.School of Electronics and Information, Northwestern Polytechnic University, Xi’an 710072，China; 2.School of Astronautics，Northwestern Polytechnieal University, Xi’an 710072，China)

The radar detection performance of the partly copied signal has not be studied at present. The partly copied signal detection performance analysis method was presented in this paper. The routine partly copied signal and LFM signal were modeled and the detection performance of radar were studied. The results of the simulation indicated that the two kind signals could be detected by radar. The finding probability of the partly copied signal was very close to the original signal at a likely copied length and SNR.

partly copied signal; LFM signal; detection performance; jamming effective

2016-12-17

国家青年科学基金项目资助(61401361)

杨立明(1976—)，男，河北赵县人，博士，研究方向：雷达信号处理。E-mail:ylmw@163.com。

TN957.51

A

1008-1194(2017)03-0041-07