后向预测高斯混合概率假设密度滤波算法

赵 凯，胡建旺，吉 兵

(解放军军械工程学院，河北 石家庄 050003)

后向预测高斯混合概率假设密度滤波算法

赵 凯，胡建旺，吉 兵

(解放军军械工程学院，河北 石家庄 050003)

针对单步延迟无序量测条件下多目标跟踪中，概率假设密度滤波对目标数量与状态估计误差偏大问题，提出了后向预测高斯混合概率假设密度滤波算法(BP-GMPHD)。该算法在后向预测框架内，以高斯混合概率假设密度滤波器为基础滤波算法，计算各高斯分量的回溯状态并进行再更新，经剪枝与合并等步骤获得最终的目标数量与状态估计。仿真验证表明，该算法在无序量测条件下保持了良好的滤波性能，能够准确估计多目标数目和状态。

多目标跟踪；无序量测；单步延迟；高斯混合；后向预测

0 引言

2003年，Mahler[1]提出了基于随机有限集(Random Finite Sets, RFS)的概率假设密度(Probability Hypothesis Density, PHD)滤波，以实现对多目标的跟踪，即将目标的状态和观测看作随机有限集，传递多目标全局后验概率密度的一阶统计矩，最终获得多目标数量与状态估计。该方法可以绕过复杂的数据关联问题，适用于目标数量时变或未知的情形[2-3]。

目前，对于PHD的近似实现方法有两种：序贯蒙特卡罗(Sequential Monte Carlo, SMC)方法与高斯混合(Gaussian Mixture, GM)方法[4-5]。由于高斯混合方法的计算量相对较小且精度较高，因此其被广泛应用于求解PHD中。

在跟踪过程中，传感器量测或因随机的通信延迟出现无序现象，即来自同一目标的较早时刻量测在较晚时刻量测之后到达融合中心[6]。Hilton[7]将这些量测命名为无序量测(Out-of-sequence Measurement, OOSM)，并针对线性高斯系统中单目标跟踪问题，在后向预测框架内提出了适用于单步延迟OOSM的B1算法，可有效降低OOSM的影响。而在多目标跟踪中，标准的PHD滤波算法无法直接处理此类“负时间更新”问题，需进行改进。

针对上述问题，提出了后向预测高斯混合概率假设密度滤波(BP-GMPHD)算法。

1 RFS与PHD滤波原理

tk时刻的多目标状态模型可用RFS描述为[9]：

(1)

式中，Xk-1为tk-1时刻的目标状态RFS；Sk|k-1表示从tk-1到k时刻存活目标状态RFS；Bk|k-1为tk-1到k时刻由Xk-1衍生的目标状态RFS；Γk为tk时刻新生目标状态RFS。

k时刻目标量测模型用RFS描述为[9]：

(2)

式中，Ck为杂波与虚警量测RFS；Θk为Xk的量测RFS。

根据经典Bayes估计理论，基于RFS的多目标Bayes估计表示为：

(3)

(4)

式中，pk|k-1与pk为多目标先验、后验概率；fk|k-1为状态转移概率；gk为量测似然函数；μ为某一空间近似勒贝格测度。

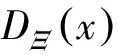
(5)

PHD可滤波器主要通过预测过程与更新过程来实现递推，其预测PHD可表示为：

(6)

式中，bk|k-1为存在目标所衍生的目标PHD；γk(xk)为新生目标的PHD；f(xk|xk-1)为状态转移概率密度。

更新PHD可表示为：

(7)

2 多目标OOSM问题描述

假定目标i的状态方程与量测方程为：

(8)

(9)

如图1所示，假设tk时刻，已有目标i的状态估计与误差协方差矩阵：

(10)

随后，来自t=td时刻的量测

(11)

3 基于后向预测的BP-GMPHD滤波算法

3.1GMPHD多目标滤波算法

文献[11]给出了GMPHD滤波器具有强L1一致收敛性质的证明。因此，高斯混合方法的引入，可避免PHD滤波问题中的复杂的积分运算。另外，应用GMPHD滤波算法时，除PHD滤波器常用假设之外，还需要满足：

1)单目标的马尔科夫转移密度和似然函数都是线性高斯的；

2)目标的存活概率PS为常数；检测概率PD为常数；

3)目标新生和衍生过程的PHD都是高斯混合形式；

(12)

式中，Jk-1为高斯混合分量个数。

3.1.1 预测步

tk时刻预测强度为：

Dk|k-1(x)=γk(x)+Ds,k|k-1(x)+Db,k|k-1(x)

(13)

式中，γk(x)、Ds,k|k-1(x)与Db,k|k-1(x)分别表示新生目标密度、存活目标和衍生目标的PHD，即

(14)

(15)

(16)

各分量具体形式可表示为：

更进一步地，预测步PHD可表示为：

(17)

式中，Jk|k-1=Jb,k|k-1+Jγ,k+Jk-1。

3.1.2 更新步

经过更新，tk时刻后验强度为：

(18)

(19)

3.2 后向预测滤波过程

Hilton提出的后向预测法，可解决卡尔曼滤波算法体系下单步延迟OOSM。其基本思想是：当系统接收到OOSM时，计算OOSM发生时刻的回溯状态与协方差矩阵等，再利用滞后到达的量测对最新时刻状态估计与协方差进行更新，可在过程噪声连续离散化模型(Discrete Continuous-time Model, DCM)条件下达到最优。具体过程如图2中步骤①②所示。这一过程还可表述为：

(20)

卡尔曼滤波体系下后向预测的算法具体过程如下[12]：

tk到td时刻的回溯状态为：

(21)

回溯相关的协方差矩阵为：

(22)

(23)

(24)

回溯量测值协方差为：

(25)

tk时刻的状态和量测值之间的协方差：

(26)

滤波增益为：

改革开放后，我国农村社会结构发生了变迁：人口老龄化、村庄空心化、邻里关系冷漠化。历史遗留问题、自然灾害、劳动力外流、生产生活方式突变等都容易造成农村社会的不稳定性。怎样带动邻里交往、增强村民凝聚力？建筑师从不同的角度切入，提供了多种可行之路。

(27)

含zd的最新时刻状态估计为：

(28)

最新时刻状态估计协方差矩阵为：

(29)

3.3BP-GMPHD滤波算法

为解决线性系统无序量测条件下的GMPHD滤波问题，提出后向预测BP-GMPHD滤波算法。 将最新时刻每一个高斯分量纳入后向预测框架内，计算OOSM发生时刻的回溯状态，并利用滞后到达的量测对其进行更新，最终通过剪枝与合并、状态提取等步骤得到更新后的状态估计与目标数量。图3给出了算法流程图。

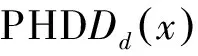
另外设定门限Tmerg，当两个分量合并距离小于此门限时，将会合并成单个分量。经过此步，得到Jk个高斯分量。

4 仿真验证

以二维平面内多目标运动情形为例，通过仿真实验综合验证BP-GMPHD算法在无序条件下的跟踪性能，并忽略OOSM的处理方式，即丢弃滞后量测法与真实值做对比，以验证算法的有效性。

4.1 参数设置

假设目标的监测区域为[-100 m,100 m]×[-100 m,100 m]的二维平面，对应的目标状态方程为

(30)

空间中有4个目标在运动，相继出现或消失。传感器对4个目标进行观测，得到的量测为其位置的二维坐标。假设每次扫描的杂波数服从泊松分布，且该过程中忽略衍生目标出现，则传感器量测方程可表示为

(31)

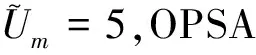
4.2 仿真一

在跟踪过程的前10s，传感器获得10个量测。假设出现OOSM，融合中心最终收到的量测序列如表1所示。

表1 单步延迟无序量测时序表

首先对该量测序列应用GMPHD-A1算法。图4为OOSM产生时刻的回溯状态集与正常时序下该时刻的状态集对比。由于算法假设回溯到OOSM产生时刻的高斯分量数量与最新时刻相同，故回溯状态集中元素数量要远少于正常时序处理的情形。图5为更新后的最新时刻状态集进行剪枝与合并前后对比，经过此步骤后高斯分量数大幅减少。

再用丢弃滞后量测法对表1所示量测进行处理，将两种算法在t=6与t=9时刻的位置分量均方根误差(RMSE)及目标数量与真实值作比较，结果如表2、表3所示。表中括号内数值是该指标相对于真实值的误差，误差越小，跟踪精度越高。可以看出，BP-GMPHD的RMSE远低于丢弃滞后量测法，即跟踪精度较高；且丢弃滞后量测法在目标数量估计上出现了偏差，此项的RMSE数值忽略了误差较大的目标。随着滤波过程的进行，OOSM的影响下降，丢弃滞后量测法与BP-GMPHD精度的差距减小，这也符合文献[9]的相关结论。

表2 t=6时刻结果

表3 t=9时刻结果

4.3 仿真二

现将跟踪时间延长至35 s，即融合中心收到35个量测。假设每7个量测中包含一个单步延迟的OOSM。分别使用BP-GMPHD算法与丢弃滞后量测法处理上述量测，将滤波结果与目标真实运动轨迹、数量做比较，结果如图6、图7所示。

图6表示多目标真实航迹与不同算法状态估计的对比。由图中可以看出，尽管多目标的量测数据中含有多个OOSM，但在使用BP-GMPHD算法滤波后，这些OOSM被应用到了状态更新中，得到的多目标的状态估计量可以很好地跟踪目标的真实运动状态，表明了该算法的有效性 。

图7给出了在不同时刻量测数据经过BP-GMPHD算法处理得到的目标数量与丢弃滞后量测法及真实值的对比，算法对目标数目的估计基本接近真实值，优于丢弃滞后量测法，目标的数目估计更加准确。

5 结论

本文提出了BP-GMPHD滤波算法。该算法在后向预测框架内，以高斯混合概率假设密度滤波器为基础滤波算法，计算各高斯分量的回溯状态并进行再更新，经剪枝与合并等步骤获得最终的目标数量与状态估计。仿真结果表明， BP-GMPHD算法在无序量测条件下保持了良好的滤波性能，具有广泛的应用价值。

需要注意的是，本文只能对单步延迟OOSM进行处理；当延迟步数多于一步时，对于回溯高斯分量的预测误差偏大，导致整体滤波结果与真实值有较大差距。因此，如何将应用范围推广至多步延迟OOSM，还需要进一步研究。

[1]Mahler R P S. Multitarget Bayes Filtering via First-Order Multitarget Moments [J]. IEEE Transactions on Aerospace & Electronic Systems Aes, 2003, 39(4):1152-1178.

[2]郝燕玲，孟凡彬，周卫东，等. 多目标跟踪的高斯混合概率假设密度滤波算法[J]. 弹箭与制导学报，2010，30(3):35-40.

[3]孔云波，冯新喜，危璋.利用高斯混合概率假设密度滤波器对扩展目标量测集进行划分[J]. 西安交通大学报，2015(7):126-133.

[4]Vo B N, Singh S, Doucet A. Sequential Monte Carlo methods for multi-target filtering with random finite sets[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4): 1224-1245.

[5]Vo B N, Ma W K. The Gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Signal Processing,2006,54(11):4091-4104.

[6]王炜,黄心汉,王敏.无序量测滤波更新算法综述[J].控制与决策,2012,27(1): 1-5.

[7]Hilton R D, Martin D A, Blair W D. Tracking with time-delayed data in multisensor systems[J]. 1993.

[8]占荣辉. 非线性滤波理论与目标跟踪应用[M]. 北京：国防工业出版社, 2013.

[9]Orton M, Marrs A. Particle filters for tracking with out of-sequence measurements[J]. IEEE Trans on Aerospace and Electronic Systems, 2005, 41(2): 673-702.

[10]马勒. 多源多目标统计信息融合[M]. 北京：国防工业出版社, 2013.

[11]Daniel Clark, Ba-Ngu Vo. Convergence Analysis of the Gaussian Mixture PHD Filter[J].IEEE Transactions on Signal Processing,2007,55(4):1204-1212.

[12]陈金广. 目标跟踪系统中的滤波方法[M]. 西安：西安电子科技大学出版社, 2013.

BP-GMPHD Filter Algorithm with Single-step-lag Out-of-sequence Measurement

ZHAO Kai, HU Jianwang, JI Bing

(Ordnance Engineering College of PLA, Shijiazhuang 050003, China)

In multi-target tracking process with one-step-lag out-of-sequence measurement (OOSM), probability hypothesis density may cause low estimation precision for target number and state. To solve the problem, a backward prediction Gaussian mixture probability hypothesis density (BP-GMPHD) filtering was proposed. Within the backward prediction framework, taking Gaussian mixture probability hypothesis density as basis filtering algorithm, backtrack state of each Gaussian component was calculated to obtain target number and state estimation after pruning and merging，etc. Simulation results showed that the proposed algorithm could effectively keep a good filtering performance with OOSM and accurately estimated the multi-target number and state.

multi-target tracking; OOSM; one-step-lag; Gaussian mixture; backward prediction

2017-01-24

赵凯(1991—)，男，山东济南人，博士研究生，研究方向：指挥信息系统与安全技术。E-mail:609587194@qq.com。

TP391

A

1008-1194(2017)03-0118-06