基于改进Elman神经网络的目标威胁度预测评估

徐公国，段修生

(解放军军械工程学院，河北 石家庄 050003)

基于改进Elman神经网络的目标威胁度预测评估

徐公国，段修生

(解放军军械工程学院，河北 石家庄 050003)

针对地面防空作战中目标威胁度难以准确评估的问题，提出了基于改进Elman神经网络的目标威胁度动态预测评估方法。该方法利用量子粒子群智能优化(QPSO)算法对Elman神经网络进行了改进，提出了QPSO-Elman神经网络，并基于优化的QPSO-Elman神经网络构建了目标威胁度的动态预测评估模型。仿真分析表明，该方法有效解决了目标威胁度的动态评估问题，预测结果更加准确且实用性强，增强了防空系统的作战能力。

目标威胁度；Elman神经网络；量子粒子群优化算法；防空作战

0 引言

在地面防空武器系统中，特别是防空C3I系统中，目标威胁度评估是武器-目标配对问题中的关键技术。只有对来袭目标的威胁度进行准确评估，才能为多目标准确配置防空武器，进而实现对重点目标进行精确打击。目标威胁度评估是涉及多层次的、动态的不确定性知识推理问题，目前主要有模糊推理[1]、层次分析[2]、多属性决策[3]、专家系统[4]、贝叶斯推理[5]和神经网络[6]等求解方法。模糊推理方法适用于数据模糊情况，有很强的泛化能力,但结果不够精确；层次分析和多属性决策方法简单，但会耗费大量计算时间；专家系统和贝叶斯推理虽为智能算法，但时需要事先设置固定的模型推理结构，系统的动态适应能力不强。

神经网络是近年来一种新型智能求解算法，能够动态自适应建模且具有很强的学习能力，成为新的研究热点，在模式识别、控制和预测等领域得到了广泛应用，并取得良好的效果。由于Elman神经网络强大的适应能力和学习能力，针对战场环境下数据的动态多变性，相比层次分析、专家系统、模糊推理等方法能够更好地解决该问题。但是与传统神经网络一样，Elman神经网络也存在收敛速度慢、容易陷入局部最小值等缺点。现有的改进方法多针对算法原理和网络结构进行，这两种改进策略算法复杂度较大，适用性不强且不易工程实现。本文针对上述问题，提出了基于改进Elman神经网络的目标威胁度预测评估方法。

1 目标威胁度影响因素和基本理论

1.1 目标威胁度影响因素的选取

影响目标威胁度评估的因素有很多，针对不同的作战任务的侧重点也会不一样。针对地面防空作战的特点，目标威胁度主要根据目标类型，目标的速度、航向、距离，是否有攻击意图以及目标的干扰能力等因素综合确定的。

目标类型：常见目标类型有轰炸机、战斗机、侦察机、直升机等各类飞机以及各种导弹等，不同类型的目标对我方的威胁程度截然不同。一般情况下，轰炸机、战斗机、侦察机、直升机对我方的威胁程度依次减小。

目标速度：目标飞行速度越大，说明处理防御的时间越少，则其威胁程度越高。

目标航向：目标航行的方向与目标和防空区域中心连线的夹角越小，目标的攻击意图越明显，目标的威胁度越大。

目标机动方式：机动方式指相对于防空区域的机动方式，一般分为巡航、盘旋、俯冲。其中俯冲的攻击意图最明显，目标的威胁程度最大，盘旋次之，巡航最小。

目标距离：目标距离是指目标与防空区域边界的距离，目标距离越小，目标的威胁度越高。

目标飞临时间：飞临时间是指目标到达防空火力发射区近界的时间，其值越小，武器系统和战术决策的准备时间越短，目标的威胁度就越高。

目标的干扰能力：干扰能力是指目标对我方武器装备实施电子干扰的能力，干扰能力越强，目标威胁程度越高。

目标的抗干扰能力：抗干扰能力是指目标对抵御我方电子干扰的能力，同样抗干扰能力越强，目标威胁程度越高。

除此之外，为更加符合实际战场环境，还需要考虑目标携带的武器，目标的战术编队，打击目标的火控需求等其他因素。

1.2 Elman神经网络

Elman神经网络[7]是一种典型的动态的神经网络，它是在BP网路的基本结构的基础上，通过内部存储状态使其具备映射动态特征的功能，从而使系统具有适应时变特性的能力。

如图1所示， Elman神经网络的结构与BP神经网络不同的是Elman神经网络分为了四层即输入层、隐含层、承接层和输出层。其中隐含层单元的传递函数可以采用线性或非线性函数，承接层用来记忆隐含层单元前一时刻的输出值并返回给网络的输入，可以认为是一个演示算子。Elman神经网络这种自联式的结构使其对历史状态的数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到动态建模的目的。

Elman神经网络的非线性状态表达式为：

y(k)=g(w3·x(k-1))

(1)

(2)

(3)

其中，w1为承接层与隐含层之间的连接权值，w2为输入层与隐含层之间的连接权值，w3为隐含层与输出层之间的连接权值，且一般情况下权值w1取单位阵。Elman神经网络权值修正算法与BP神经网络相同，均为梯度下降法，误差函数则为：

(4)

1.3QPSO优化算法

与BP神经网络一样，Elman神经网络仍然采用梯度下降法进行权值、阈值的误差修正，容易陷入局部最小值，且对初始权值、阈值的依赖性很强。然而，实际算法中，初始权值、阈值的设置是随机产生的，对测试数据的适应性无法得到保证，从而会影响到最终的训练结果。因此引入QPSO智能优化算法对Elman神经网络初始权值、阈值进行优化，从而使神经网络有更好的预测效果。

针对普通粒子群优化(PSO)算法全局寻优能力不佳的缺陷，SunJun等[8]在量子理论的基础之上，提出了具有量子行为的粒子群优化(QPSO)算法。与普通PSO算法相比，QPSO算法因引入量子特性，粒子以概率的方式出现在某个位置上，没有了固定的运动轨迹和限制区域，这就使得粒子可以在整个解空间中进行搜索，极大地提高了粒子的全局寻优能力。 该模型中粒子的位置由波函数来描述，粒子的状态变化则由薛定谔方程决定。通过蒙特卡罗随机模拟的方法得到粒子的位置方程为：

x(t)=Q±L/2ln(1/μ)

(5)

其中，μ是在[0,1]上服从均匀分布的随机数，L、Q则由下面的公式计算而来。

(6)

Q(t)=φpib(t)+(1-φ)pgb(t)

(7)

其中，β为收缩扩张因子，通常情况下随着迭代次数线性地从1递减到0.5，计算公式为：β=1-0.5(iter/iterm)，式中iter是当前迭代次数，iterm是最大迭代次数。mbest是粒子群pbest的中间位置，即平均值，计算公式为：

(8)

其中，φ是在[0,1]上服从均匀分布的随机数，pib(t)表示第t次迭代时第i个粒子的当前最优位置，pgb(t)表示第t次迭代时所有粒子的全局最优位置。进而粒子的位置更新方程为：

(9)

其中，rand(t)的取值如下式所示：

(10)

其中，λ是随机产生的随机数，且在[0,1]上服从均匀分布。

2 基于QPSO-Elman神经网络的目标威胁度预测评估方法

2.1 基于QPSO的改进Elman神经网络

现阶段，对神经网络的改进主要集中在算法原理和网络结构的改进，复杂度高且不易实现。因此，本文利用QPSO算法对Elman神经网络的参数选择进行优化，该优化策略原理简单易于工程实现，有很大的工程应用价值。之所以采用QPSO智能优化算法，是因为QPSO算法有更好的寻优性能。而传统PSO算法有收敛速度较慢，全局寻优能力不强，易陷入局部最优等缺点[9-12]。

利用QPSO优化Elman神经网络首先要解决的是如何用粒子来表示神经网络的权值和阈值，以便进行优化搜索。考虑到Elman有w1、w2、w3三类连接权值，除此之外还需要设置隐含层和输出层的阈值，取隐含层阈值数组为φ1，输出层阈值数组为φ2。则粒子位置编码可表示为：

x=[w1,w2,w3,φ1,φ2]

(11)

若输入层、隐含层和输出层的数目分别为n1、n2、n3，则经计算粒子的维数为n1·(n1+n2+n3)+n2+n3。QPSO-Elman神经网络算法的具体流程如图2所示。

2.2 目标威胁度预测评估方法的求解步骤

至此，进行目标威胁度评估的核心算法已经设计完毕，下面给出基于QPSO-Elman神经网络进行目标目标威胁度评估预测的具体步骤。

步骤1：依据历史作战数据，获得目标威胁度评估的经验数据，即训练数据和测试数据；

步骤2：Elman神经初始化设置，网络结构的搭建，输入层、隐含层、输出层数目的确定，误差迭代次数、迭代精度及传输函数的设置；

步骤3：QPSO的初始化，包括粒子群的数目与初始值，初始收缩扩张因子β，最大迭代次数iterm，全局最优pgb(t)和当前最优pib(t)的初始值；

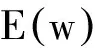
步骤5：判断适应值是否达到精度要求，迭代步数是否达到最大迭代次数iterm，否则利用式(9)对粒子进行更新，并返回步骤3对下一代粒子进行适应值判断；

步骤6：迭代结束，将最优粒子值赋给神经网络权值和阈值，再用全部测试数据进行大规模的训练，最后得出优化训练的神经网络；

步骤7:利用训练后的神经网络进行目标威胁度预测，当有新的目标出现时，只需将目标的参数值输入训练后的神经网络即可得到目标威胁度值。

3 仿真实验与分析

在上文研究的基础上，我们了解了影响目标威胁度的各种因素，并设计了目标威胁度的预测评估求解算法。下面将通过实例详细分析目标威胁度评估预测的过程，并对QPSO-Elman神经网络改进算法进行性能评估。

采集20组数据来训练神经网络，数据如表1所示，考虑的目标威胁度影响因素有目标类型、目标速度、目标航向、目标距离以及目标干扰能力。此外，表中目标威胁度值获取于参考文献[11]，一般根据历史经验由各影响因素线性加权得来。针对目标类型和干扰能力非定量属性，需设定相应的量化标准，以便于数据处理。对于目标类型轰炸机、战斗机、直升机、侦察机，依次量化为8,6，4，2；干扰能力强、中、弱则依次量化为9，6，3。

神经网络隐含层的激活函数多采用sigmoid函数，净输入数据的绝对值过大会使神经元输出饱和，进而使权值调整进入误差曲面的平坦区。因此，为了保证神经网络的稳定运行、提高网络的学习速度和网络精度，对样本数据进行归一化处理。本文采用将输入输出数据变换到0至1之间的处理方法，计算方法式(12)所示。

X*=(X-Xmin)/(Xmax-Xmin)

(12)

其中，Xmax为输入数据的最大值，Xmin为输入数据的最小值，X为原始数据，X*为归一化后的数据。

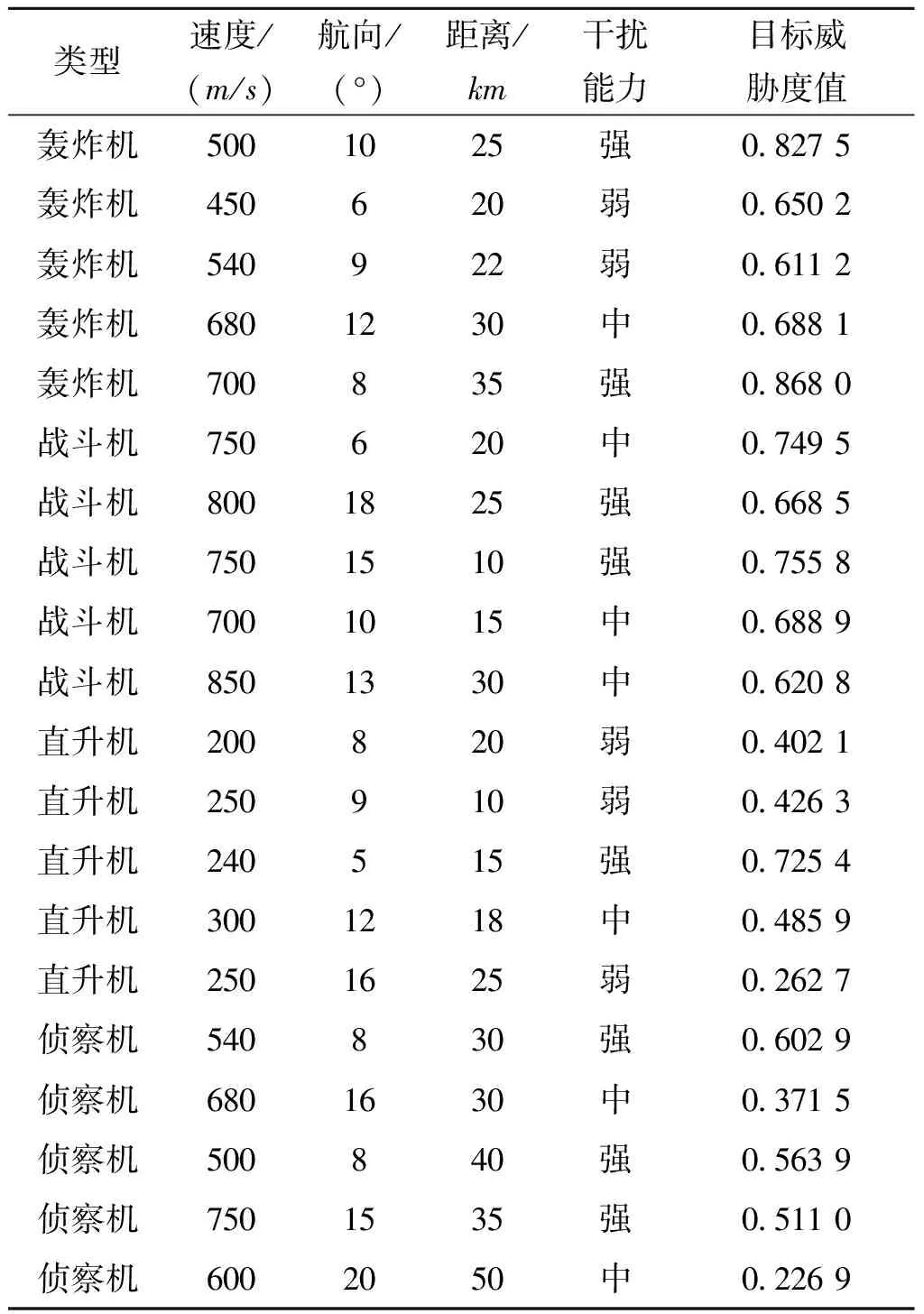
表1 训练数据

(13)

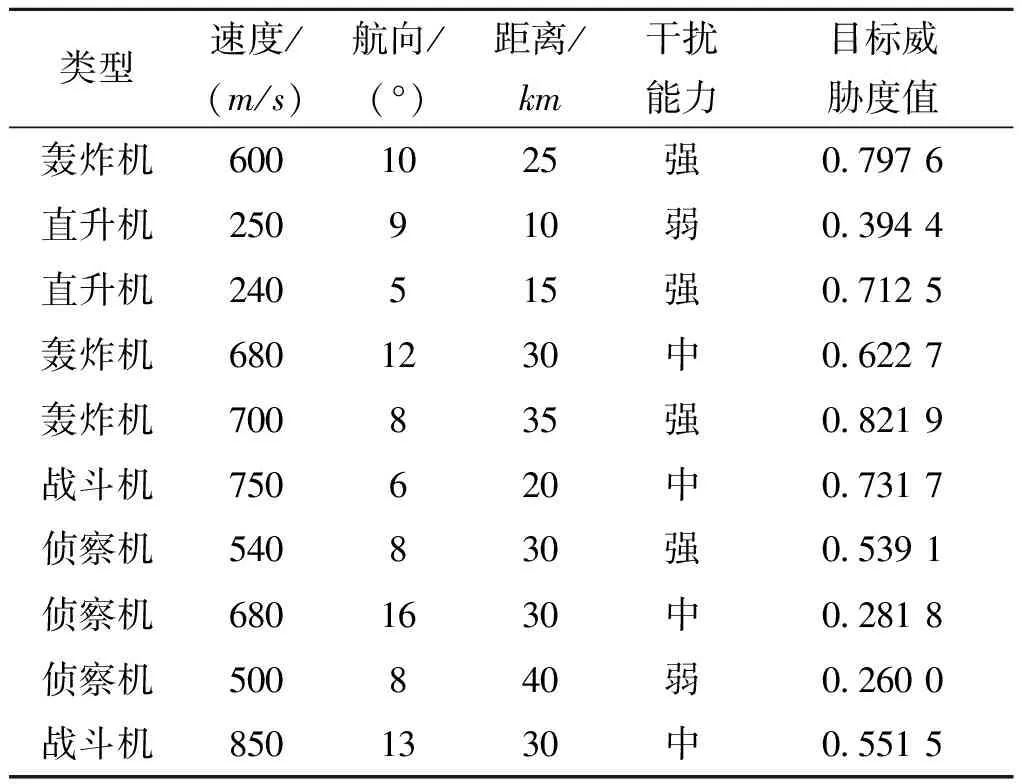
表2 测试数据

此外，神经网络训练迭代次数为1 000次，重复运行次数100次。QPSO-Elman神经网络中，粒子群的数目取为100，最大迭代数为100，收缩扩张因子β=1-0.5(iter/iterm)，短期训练迭代步数为100。实验结果如表3所示，预测误差适应值收敛曲线如图3所示。

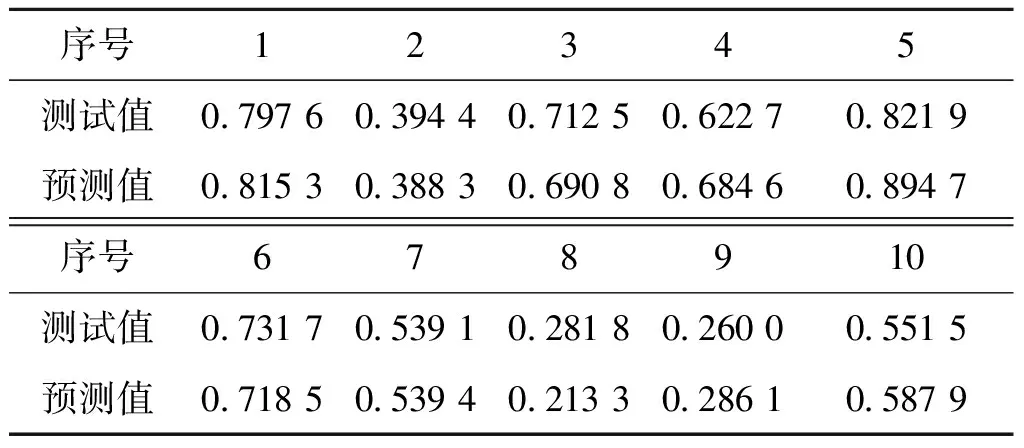
表3 QPSO-Elman神经网络目标威胁度预测值

由表3易得在误差允许范围内，QPSO-Elman神经网络能够实现快速准确地对目标威胁度的准确预测评估，能够满足防空作战的需求，由此说明构建的模型是行之有效的。

由图3可见，通过引入QPSO优化算法使得Elman神经网络的预测误差得到有效的收敛，且能在较短迭代步数内达到误差精度要求。此外，通过实验发现，相较于标准粒子群算法，QPSO优化算法有更强的全局搜索能力，对于Elman神经网络的优化效果更好。

改进后的QPSO-Elman神经网络与BP神经网络和标准Elman神经网络预测误差对比如表4和图4所示，可以看出改进后的QPSO-Elman神经网络预测误差更小，且有更强的稳定性。

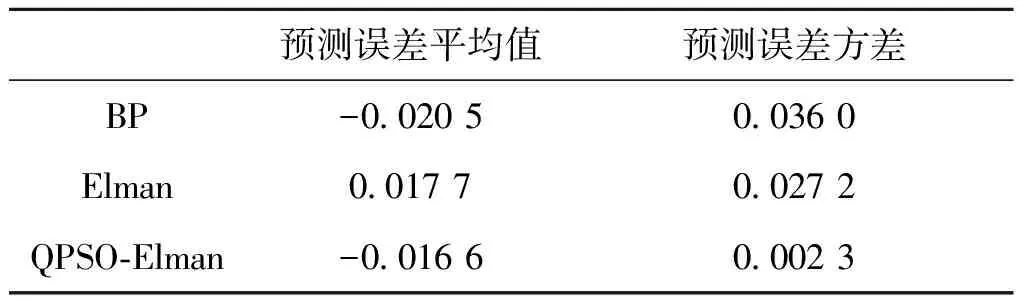
表4 预测误差比较

4 结论

本文提出了基于改进QPSO-Elman神经网络的目标威胁度预测评估求解办法。该方法利用QPSO智能寻优算法对Elman神经网络进行了改进，提出了QPSO-Elman神经网络，并基于优化的QPSO-Elman神经网络构建了目标威胁度预测评估模型。仿真分析表明，QPSO-Elman神经网络的初始参数设置更加合理，预测结果也更加准确；相较于传统的目标威胁度评估办法，所建模型有着很强的动态适应能力，比较符合战场需求且易于工程实现，对优化整个地面防空武器系统的作战性能有着重要的作用。

[1]童俊,单甘霖. 基于Vague集的TOPSIS法求解目标优先级[J]. 火力与指挥控制, 2012(5):140-143.

[2]陈秀真,郑庆华,管晓宏，等.层次化网络安全威胁态势量化评估方法[J].软件学报, 2006, 17(4):885-897.

[3]鲁华,周德云. 基于灰色分析的对地多目标攻击战术规划研究[J].计算机工程与应用, 2011(4):239-241.

[4]刘顺利,陈亚生,陈琳. 基于Agent的空中目标威胁度评估模型[J].弹箭与制导学报, 2010(6):212-215.

[5]杨健,高文逸,刘军.一种基于贝叶斯网络的威胁评估方法[J].解放军理工大学学报(自然科学版), 2010, 11(1):43-48.

[6]江克宇,冯根生,龚建辉. 坦克火力运用智能系统目标威胁度评估模块[J]. 火力与指挥控制, 2013(7):135-137.

[7]郭娇娇.基于改进Elman神经网络的短期电力负荷预测[D].沈阳：沈阳工业大学，2015.

[8]Sun J. A global search strategy of quantum behaved particle swarm optimization[C]//Proceedings of IEEE conference on Cybernetics and Intelligent Systems, 2004: 111-116.

[9]田路,张炜,杨正伟. Elman型神经网络在液体火箭发动机故障预测中的应用[J]. 弹箭与制导学报, 2009(1):191-194.

[10]刘实,闫岩,徐立新. 静电探测器信号采集与目标特性预测方法研究[J]. 探测与控制学报, 2007,29(2),20-22.

[11]王改革,郭立红,段红,等. 基于Elman_AdaBoost强预测器的目标威胁评估模型及算法[J]. 电子学报, 2012(5):901-906.

[12]宋玉琴,章卫国. 基于混合粒子群算法的小波神经网络故障诊断[J]. 测控技术, 2011(1):112-116.

Target Threat Prediction Assessment Based on Improved Elman Neural Network

XU Gongguo, DUAN Xiusheng

(Ordnance Engineering College of PLA, Shijiazhuang 050003, China)

Aiming at the problem that target threat is hard to assess in ground air defense operation, a method of target threat assessment was proposed based on the improved Elman neural network. The Elman neural network was improved based on the quantum particle swarm optimization (QPSQ), and the QPSO-Elman neural network was proposed. Besides, a assessment model was proposed based on QPSO-Elman neural network. The simulation results showed that this method could effectively solved the problem, the prediction results were more accurate and practicable, and it could enhance the operational capability of the air defense system.

target threat assessment; Elman neural network; quantum particle swarm optimization; air defense operation

2017-01-11

军内科研基金重点项目资助(ZS2015070132A12009)

徐公国(1990-)，男，山东滕州人，硕士研究生，研究方向：传感器管理、多源信息融合、防空武器系统仿真与应用。E-mail：xugguo@yeah.net。

TP183

A

1008-1194(2017)03-0101-06