基于刚柔耦合模型的汽车排气系统运动包络面仿真方法＊

吴杰 黄思良

（华南理工大学，广州 510641）

基于刚柔耦合模型的汽车排气系统运动包络面仿真方法＊

吴杰 黄思良

（华南理工大学，广州 510641）

将经过自由模态试验验证的排气系统有限元模型导入ADAMS虚拟样机平台，建立了更接近实际结构的动力总成-排气系统刚柔耦合仿真模型。在汽车极限载荷工况下计算了排气系统上4个关注点的位移，将刚柔耦合仿真方法与传统有限元方法的仿真结果相比较，结果显示，两种方法的预测一致性较好，间接验证了刚柔耦合仿真方法的准确性。

1 前言

在汽车零部件正向开发过程中，车轮、发动机悬置系统以及排气系统等通常要进行运动包络面分析。黄金陵等[1]提出了车轮运动包络面的计算方法，并验证了麦弗逊悬架车轮系统跳转运动包络模型的可靠性。吴保玉等[2]建立了考虑弹性元件柔性特性的悬架多体系统模型，论述了轮胎包络空间的仿真方法，轮胎包络面更接近实车动力学特性。韦宝侣等[3]介绍了动力总成悬置系统运动包络的计算方法，并仿真分析国外某公司28种典型工况下的动力总成运动形态，为发动机周围结构的布置提供了设计依据。何森东等[4]提出了排气系统运动包络面的仿真思路，并利用该包络面进行了运动干涉校核。顾彦等[5]建立了排气系统和吊耳有限元模型，施加车辆行驶工况下的载荷，得到了排气系统运动包络面，可用于初期设计的运动干涉检查。

本文针对某车型排气系统，由自由模态试验验证了其有限元模型精度，考虑到排气系统的结构及安装特点[6]，将排气系统视为柔性体、动力总成视为刚体建立动力总成-排气系统刚柔耦合模型，该模型更接近实际排气系统动力学特性。基于国外某公司的10种极限工况分析排气系统的运动包络面，由后处理动画可以直观地判断排气系统在相应工况下的运动是否与其它零部件发生运动干涉。

2 排气系统模态分析及验证

2.1 排气系统有限元模型

在网格处理时，应使有限元模型与排气系统在受力、变形等方面表现尽量一致，网格结构形状不应破坏几何模型的原有形态。排气系统主要采用壳单元进行网格划分，有限元网格模型包含83 530个节点和78 248个单元。

2.2 排气系统自由模态分析及试验验证

自由模态分析应确保排气系统没有受到外界环境的边界约束，使其处于自由状态。自由模态分析时[7]，在Hypermesh软件环境中设置模态提取数据卡和求解控制卡片，由Nastran进行模态计算，根据试验与计算振型相似的判断原则，表1列出了各阶自由模态的计算值与试验值的对比结果。表1中第2阶和第13阶模态未能识别，其原因主要包括：波纹管、吊耳的计算所用刚度与真实刚度有所差别而导致的数值模型误差；激振器的激励位置、传感器的数量和在排气系统中的安装位置、数据采集器接口、力锤敲击力的方向及大小等对排气系统模态参数产生的影响；测试环境的影响等。

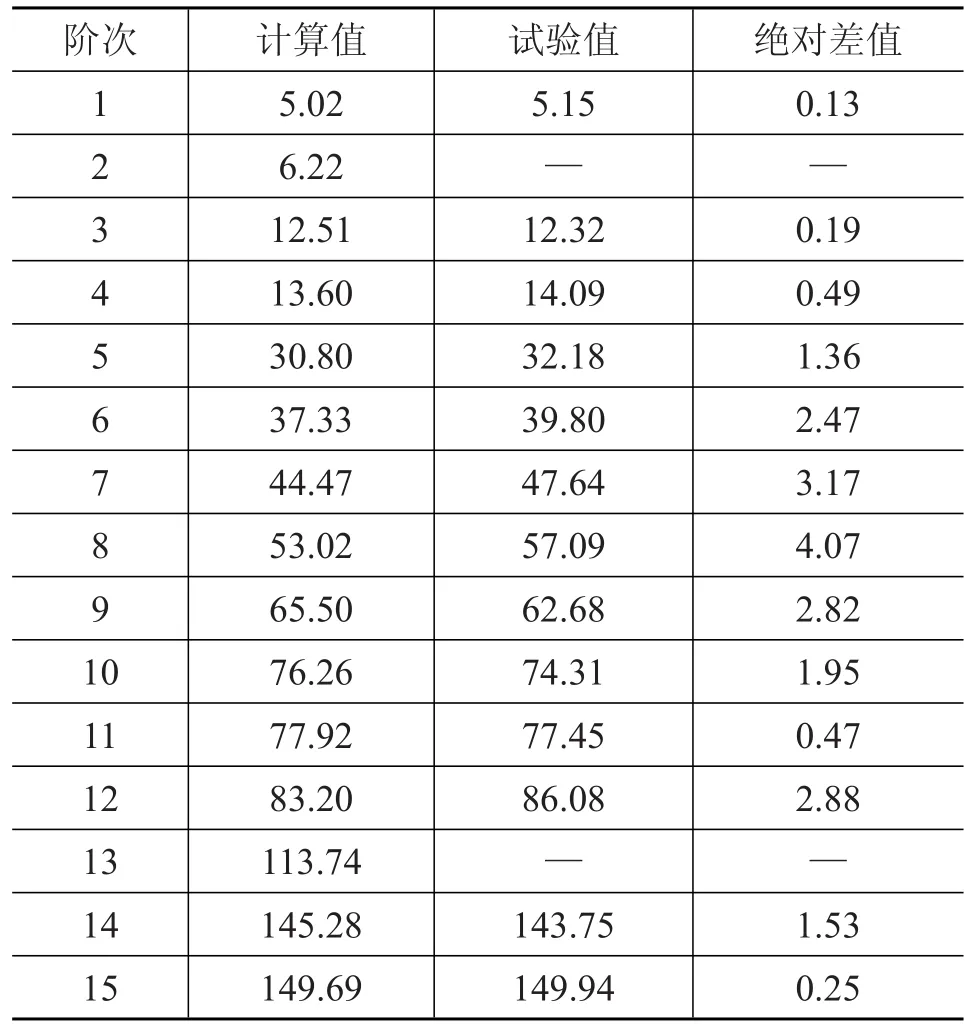
表1 排气系统自由模态频率计算值与试验值对比 Hz

由表1可知，第8阶模态频率绝对差值达到4.07 Hz，其余阶次均小于3.2 Hz，表明所建立的有限元模型与排气系统样件吻合程度较高，可用于进一步仿真计算。

2.3 排气系统约束模态分析及试验验证

约束排气系统前端法兰6个自由度，并约束吊耳与车身侧连接点的6个自由度，使用Nastran计算得到排气系统约束模态频率。为验证计算精度，测试了排气系统装车状态下的约束模态频率，试验结果与计算结果的对比如表2所示。试验车辆装配四缸四冲程汽油发动机，常用转速在6 000 r/min以下，因此重点关注0～200 Hz频率范围。

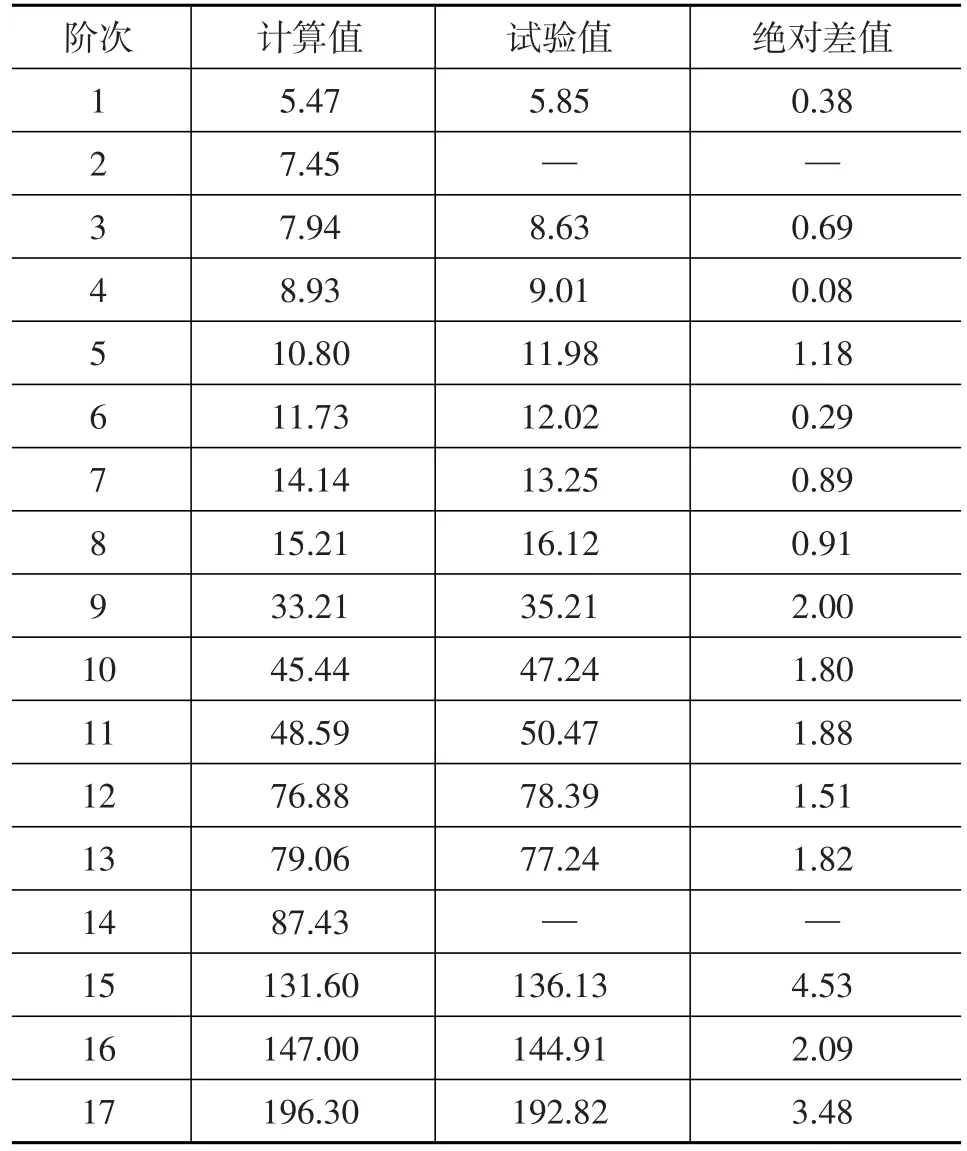
表2 排气系统约束模态频率计算值与试验值对比 Hz

同样，约束模态测试中的第2阶和第14阶模态也未能识别。此发动机怠速转速为750±50 r/min，扭矩激励频率约为23.3～26.7 Hz，与表2中的第8阶和第9阶固有频率相隔至少7 Hz，可以避开怠速共振。

3 排气系统包络面分析

3.1 动力总成-排气系统刚柔耦合模型

在Nastran中进行包络面分析时，动力总成被简化成位于其质心的质点并赋予惯性参数，然后与排气系统有限元模型连接并仿真计算。这种包络面仿真方法的弊端在于：结果中没有准确考虑动力总成惯性参数对排气系统运动的影响；包络面仿真结果只有数据而没有直观的图片或动画显示，不利于判断干涉点的具体位置及空间利用情况。为了更精准地考虑动力总成的影响，以及方便后续更高效地判断排气系统的运动干涉情况，建立了动力总成-排气系统刚柔耦合仿真模型。

动力总成与排气系统直接连接，因此进行排气系统包络面分析时，需建立动力总成和排气系统的仿真模型并正确耦合。排气系统是细长结构，弹性特征明显，因此进行包络面分析时，应对其进行有限元网格离散。动力总成的1阶弹性模态频率远大于排气系统的常见模态频率（0～200 Hz），且动力总成结构复杂，对其进行有限元离散的工作量很大且没有必要，故将动力总成视为刚体并赋予其惯性参数，可更加准确地考虑动力总成对排气系统运动包络的影响。

耦合模型的建立步骤为：

a.使用Nastran计算得到排气系统模态中性文件，在ADAMS/View中，用刚性长方体模拟动力总成，导入排气系统模态中性文件以及车身隔热罩几何文件，外连节点处施加相应的外部边界条件。

b.用Bushing弹性阻尼单元模拟动力总成悬置、排气系统波纹管及吊耳，排气歧管法兰固定连接在动力总成上。将车身底盘和车架作为刚体并固定，整个模型通过悬置和吊耳连接在底盘和车架上。

需注意的是，建模时应事先在网格模型中建立柔性体与其它零件的外连节点，并依照连接关系约束节点对应的自由度，排气系统柔性体应去除对分析工况影响很小的高阶模态频率。动力总成-排气系统刚柔耦合模型如图1所示。

图1 动力总成-排气系统刚柔耦合模型

波纹管前、后端，中间排气管路以及尾管处是位移较大的区域，易与周围的隔热罩、备胎和装饰罩等发生运动干涉。考虑到排气系统吊耳布置方案，选取4个关注点（P1～P4）提取其极限位移，如图2所示。

图2 位移关注点位置示意

3.2 极限工况计算结果及包络面分析

对排气系统进行运动包络面分析的目的是在排气系统位移波动幅度最大的行驶工况下，校核排气系统的准静态位移，确保其不与周围零部件发生干涉。这与对动力总成悬置系统进行的准静态位移校核相似，采用的模拟工况是国外某公司的28个准静态加载工况[3]，并不需要进行动力学或瞬态冲击分析。28个工况中的10个极限工况（编号10～19）对排气系统的运动干涉影响最大，因此本文只加载10个极限工况对动力总成-排气系统刚柔耦合模型进行静力学分析，计算汽车在平衡状态时关注点的静态位置。表3列出了国外某公司的10种极限工况的加载方式和工况描述，这些工况基本能够描述汽车在极限行驶过程遇到的各种情形。在Adams中将10种极限工况下的加速度载荷分别施加给整个动力总成-排气耦合系统，采取准静态求解方法，计算得到4个关注点的极限位移，结果见表4。

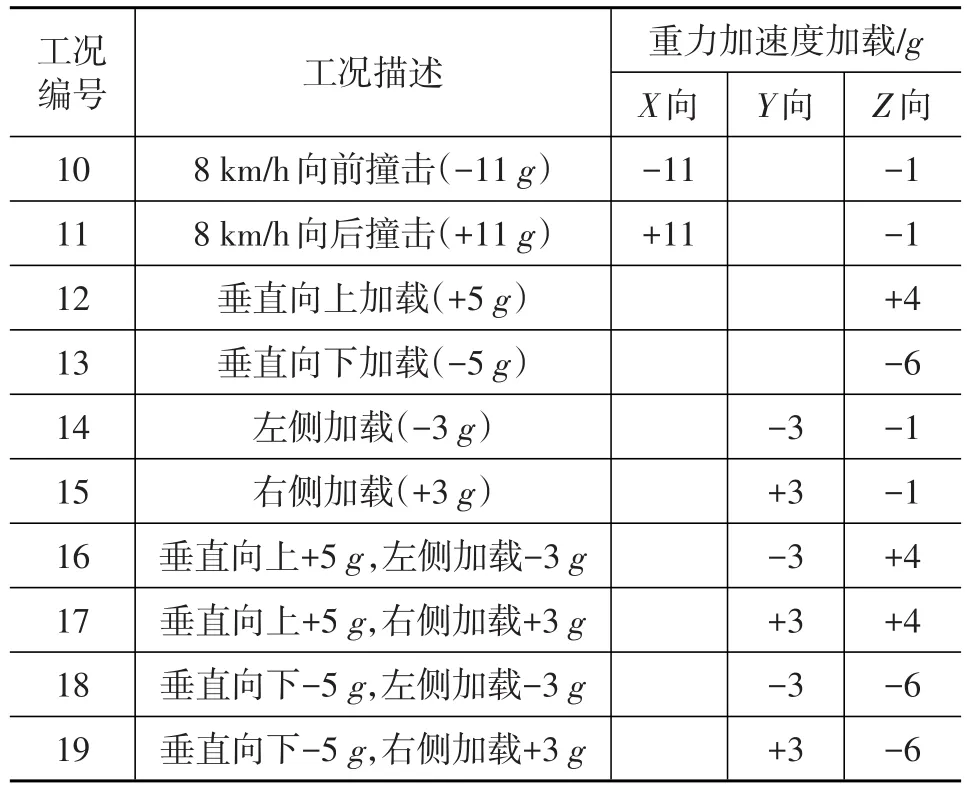
表3 国外某公司极限工况加载描述

排气歧管法兰与发动机为刚性连接，所以P1与发动机的位移很接近，而P2、P3、P4与排气系统前端之间存在挠性波纹管，在各工况下，X方向加载使得排气系统前端关注点P1和后端关注点P2、P3、P4的位移存在较明显差别。由表4还可以看出，在极限工况下，关注点的运动空间范围为：X向-61.67～61.49 mm；Y向-22.76～22.81 mm；Z向-19.68～19.59 mm。运动空间与设计值相比较偏大，有必要进行干涉检查。

以工况11和工况17为例，进行排气系统干涉分析。在Adams/PostProcessor模块中，载入工况11的运动动画，如果有干涉，则能够直观地显示排气系统与隔热罩等产生干涉的位置，图3为工况11的干涉区域。由图3可知：在Z方向，排气歧管法兰和三元催化转换器与隔热罩顶壁发生了干涉；由于排气系统后端P3处在X方向的位移达到61.44 mm，排气系统中间管路及副消声器与隔热罩侧壁也存在干涉区域。为消除干涉，建议增大波纹管X方向刚度，或者增加发动机悬置的横向刚度。

工况17Y向和Z向的位移都偏大，其干涉区域如图4所示。由图4可以看出，歧管法兰、三元催化转换器以及中间管路都与隔热罩发生了明显干涉，副消声器与隔热罩侧壁也存在干涉。为消除干涉，建议加强各吊耳的限位功能，增大限位刚度，同时，适当增加隔热罩与排气系统的间隙，也可以优化各吊耳3个方向的刚度以减轻干涉程度，但修改吊耳刚度会引起系统模态参数及隔振率的变化，需要对排气系统进行循环优化设计，使各设计目标都得以满足。

表4 关注点极限工况位移（刚柔耦合方法） mm

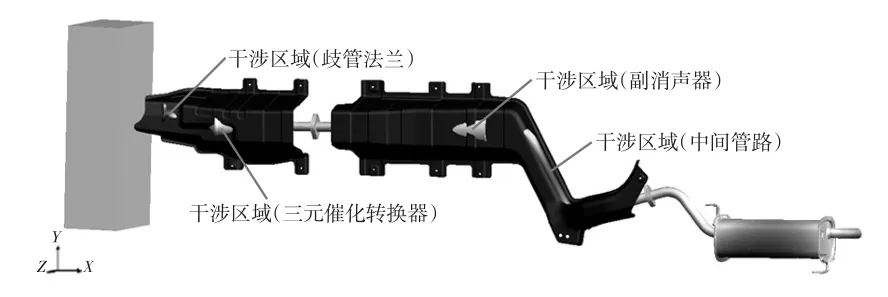
图3 极限工况11干涉区域

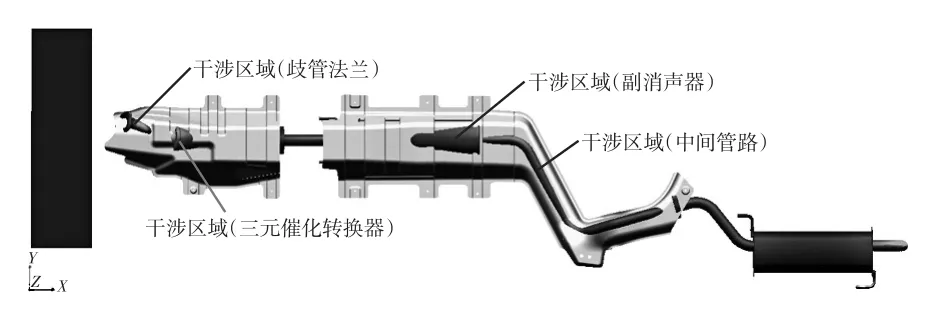
图4 极限工况17干涉区域

3.3 刚柔耦合方法的仿真对比验证

在极限工况下，实车验证排气系统包络面的计算精度有很大困难。为验证刚柔耦合方法计算的准确性，将刚柔耦合分析结果与传统的采用Nastran计算得到的包络面计算结果进行对比，可以间接验证刚柔耦合计算方法的准确性。图5为动力总成-排气系统的传统有限元模型，其中动力总成被简化成位于动力总成质心处的质量单元，赋予其质量和转动惯量等参数，排气歧管法兰刚性连接至动力总成质心。悬置、波纹管和吊耳采用CBUSH单元模拟，其它参数与刚柔耦合模型完全一致。

图5 动力总成-排气系统传统有限元模型

将表4中的位移与传统有限元方法计算获得的位移相减得到位移计算差值，结果见表5。从表5可以看出，在各极限工况下，3个方向位移差值的范围为：X向-1.00～0.87 mm；Y向-3.72～3.58 mm；Z向-6.90～7.49 mm。两种方法的位移差值仅在工况10和工况11的Z方向存在较大差别，在X和Y方向较小。其余工况下的位移差值在4 mm以下，两种方法的计算结果一致性较高，间接验证了刚柔耦合仿真方法的合理性和准确性。传统有限元方法的动力总成被简化成质量单元，并施加惯性参数，刚柔耦合方法中的动力总成用长方体刚体代替并赋予惯性参数，这造成了两种方法中的动力总成惯性参数分布不完全一致，从而导致两种计算方法存在差别。

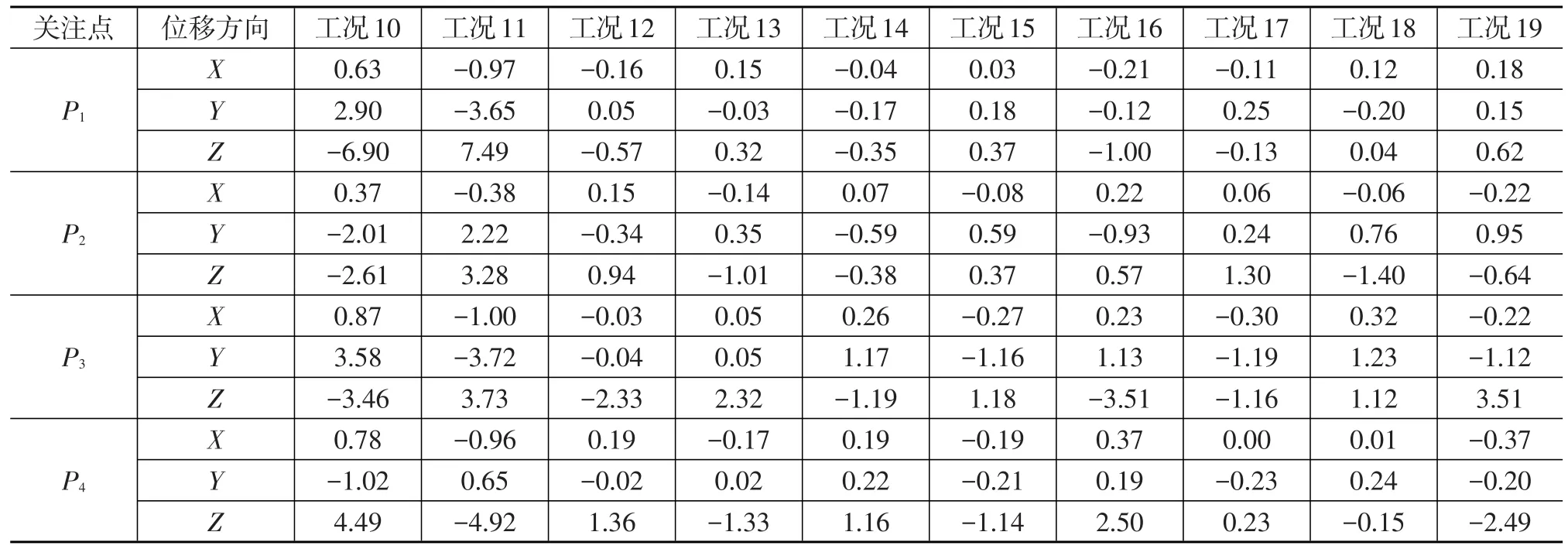
表5 两种计算方法的位移差值 mm

4 结束语

基于动力总成-排气系统刚柔耦合建模方法计算的排气系统运动位移，既考虑了动力总成的惯性参数分布，又包含了排气系统在受载时的弹性变形，结果更加精确。利用耦合模型的仿真计算结果能够以动画形式呈现，与传统有限元方法相比，可以直观地判断关注点是否存在运动干涉并优化排气系统的布置空间。对比结果表明，两种方法的预测趋势一致性很好，间接验证了刚柔耦合建模方法的准确性。

为提高仿真精度，在后续研究中将考虑橡胶吊耳和发动机悬置的非线性刚度及限位接触模拟，以及导入动力总成真实几何模型使得动力总成惯性特性的分布更加接近实际情况。

1 黄金陵，任金东，程义，等.轿车车轮运动轨迹包络面计算方法和CAD系统.汽车工程，2002，24（3）：259～262.

2 吴保玉，王建宜，王彧.柔性悬架系统下的车轮运动包络面分析.汽车科技，2013（2）：27～30.

3 韦宝侣，吕兆平.动力总成悬置系统运动包络及工况载荷计算方法.装备制造技术，2012（6）：44～47.

4 何森东，李洪亮，顾灿松.汽车排气系统包络计算与运动干涉分析.大众科技，2014，16（11）：98～100.

5 顾彦，宋艳冗，汪晓虎，等.汽车排气系统运动包络面的计算.MSC.Software中国用户论文集，2007.

6 庞剑，谌刚，何华.汽车噪声与振动：理论与应用.北京：北京理工大学出版社，2006.

7 王勖成，邵敏.有限单元法基本原理和数值方法.北京：清华大学出版社，2003.

（责任编辑 斛 畔）

修改稿收到日期为2016年11月29日。

Simulation Method of Motion Enveloping Surface for Automotive Exhaust Systems Based on Rigid-Flexible Coupling Model

Wu Jie,Huang Siliang
（South China University of Technology,Guangzhou 510641）

The exhaust system Finite Element(FE)model verified by the free modal experiment was imported to ADAMS virtual prototype platform,and the rigid-flexible coupling simulation model of the powertrain and the exhaust system were built which was more close to actual structure.Four focused points’displacements were calculated under automotive extreme load cases.The calculated results of rigid-flexible coupling method were compared with that of the traditional FE method,which showed good prediction consistency,this indirectly verified the calculation accuracy of the presented rigid-flexible coupling method.

Exhaust system,FE analysis,Rigid-flexible coupling model,Enveloping analysis

排气系统 有限元分析 刚柔耦合建模 包络面分析

U464.149

A

1000-3703（2017）06-0044-05

教育部新世纪人才计划项目（NCET-11-0157）；广东省自然科学基金项目（2016A030313463）。