基于线性损伤理论的筒形缸红套环蠕变损伤累积研究
赵仕志,刘东旗,陈铁宁,张明
(东方汽轮机有限公司,四川德阳,618000)
基于线性损伤理论的筒形缸红套环蠕变损伤累积研究
赵仕志,刘东旗,陈铁宁,张明
(东方汽轮机有限公司,四川德阳,618000)
红套环筒形缸在大功率汽轮机中使用越来越广泛,随着机组参数的升高,红套环不可避免地处于蠕变状态。合理确定红套环的初始紧力,检修周期以及保证运行的安全可靠性都必须考虑蠕变效应,但是针对红套环的蠕变损伤累积研究还比较少见。文章基于线性损伤理论,结合拉松-米勒参数法(简称L-M法)建立了红套环蠕变损伤计算的一般形式,并研究了初始紧力和大修周期对损伤累积的影响。对于理解红套环服役期内的性能退化过程和指导工程设计有显著意义。
汽轮机,红套环,蠕变损伤,损伤力学
0 引言
发展超超临界汽轮机机组,能大幅度提高单机的发电效率,以满足经济发展、环境保护及能源节约的多重需求。但随着进汽参数的不断提高,汽缸的几何尺寸相应增加,这样在机组启动、停机和变工况时,导致汽缸法兰内外壁温差过大,从而产生很大的热应力,直接影响机组的安全稳定运行[1]。红套环筒形缸结构是克服这些困难的一种可行方案,近年来得以广泛使用。
对于高温区工作的红套环来说,蠕变是不可避免的。由于蠕变效应,红套环材料中的损伤不断累积,当损伤累积到一定程度就可能导致红套环破坏,所以红套环的蠕变寿命是影响机组安全性的重要指标。从另一方面来说,红套环通常是加工精度要求极高的高温合金大锻件制品,其母材,锻冶和机加成本都非常高昂。如不能准确地预测红套环剩余寿命而提前报废将使汽轮机的运行和维护成本显著增加。因此,高温红套环的损伤累积研究和寿命评估有重要的工程意义。
目前国内外已有大量关于汽轮机部件蠕变寿命损伤的研究和报道,但是这些研究多数集中在叶片和转子[2-6]领域,也有部分文献将研究对象选定为螺栓或汽缸[5,7-9],但是对筒形缸红套环的蠕变损伤研究还比较少见。
本文基于线性损伤理论建立了红套环蠕变损伤计算的一般形式,并结合拉松-米勒蠕变模型,初步建立了红套环蠕变损伤累积和允许大修次数的计算方法。
1 理论分析
1.1 线性损伤理论
与转子部件主要载荷是恒定的离心力不同,对于红套环,其主要的载荷是由装配过盈量引起的装配应力。由于蠕变效应,红套环的应力状态在持续变化。因此在转子部件设计中常用的拉松-米勒法不能直接用于红套环的蠕变损伤和蠕变寿命分析。研究这类应力持续变化部件蠕变损伤的常用方法是寿命-时间分数法,也就是线性损伤累积法则。该方法虽然古老,且精度稍差,但是由于形式简单,计算方便,目前仍然是应用最广泛的损伤累积法则,并且是ASME列入锅炉和压力容器设计规范的唯一方法[10-11]。因此本文的研究采用该方法。
线性损伤理论认为各变应力和变应变所引起的损伤可分别计算并线性叠加。其基本公式[10]是式(1):

1.2 第一个大修周期内的损伤累积
对于本文所研究的红套环。可以假设在温度T和应力σ下红套环的蠕变断裂时间lif有如下的形式,见式(2):

首先来分析第一个检修周期t1内的情况。在红套环服役期内某时间点的时间微元dt内,因为时间很短,可认为温度T和应力σ均不变。根据式(1),在该时间微元dt内红套环的损伤可表示为式(3):

那么,红套环在第一个检修周期t1内,其累积损伤为式(4):

将式(2)带入式(4),红套环的累积损伤可表示为式(5):
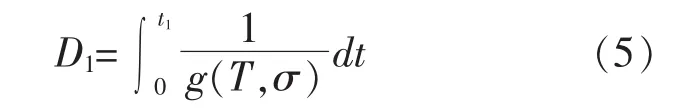
在全寿命周期内温度T和应力σ均是时间t的函数。要确定此两函数并不难[13]。特别是由于有限元技术的广泛应用,当材料和工况确定后,只需要按照热边界条件和材料的蠕变模型就可以很准确地计算出温度T和应力σ的时间历程曲线。详细的计算过程不是本文研究重点,不再赘述。最一般的情况,可以假设温度T和应力σ为如下形式的已知函数,见式(6)、式(7):

将式(6),(7)带入式(5)可得最一般的情况下,第一个检修周期t1内的总损伤为式(8):
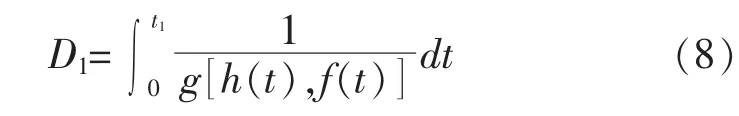
显然,式(8)其实是一个时间t的单变量函数。由于h(t),f(t)为已知函数,只要确定函数g(t)的形式就可以确定在第一个大修周期内红套环所累积的损伤。这就是红套环线性蠕变损伤累积模型的一般形式。
g(t)的确定需要知道材料的蠕变模型。由于在时间微元dt内温度和应力均可以认为是不变的,因此可以使用拉松-米勒参数进行分析和计算。
对于金属材料LMP参数方程通常可表示为式(9):
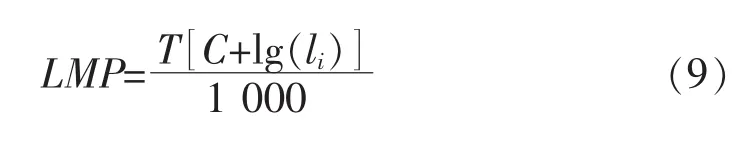
其中:
T:温度,K;
C:以材料相关的常数,通常取值在20~25;
li:载荷保持时间。
当以材料持久强度性能数据带入式(9)时有li= lif,式(9)变为式(10):
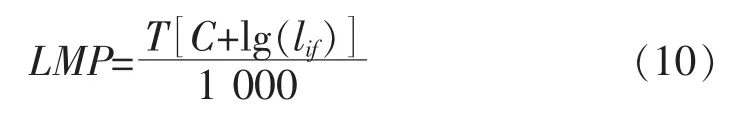
另一方面,对于确定的材料,应力和LMP参数间成确定的函数关系。对于金属材料,通常LMP和σ成二次函数关系。一般的可以假设[14]为式(11):
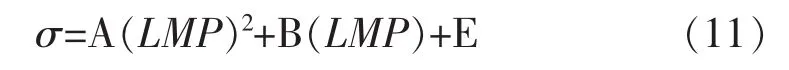
对式(11)求解LMP可得式(12):
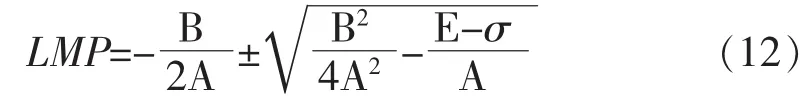
其中A,B和E是与材料相关的常数。因此,只需要知道材料3个以上不同试验工况的持久性能试验数据就可以确定这3个常数,从而确定式(11)和(12)。因此式(12)也可视为已知的。于是,将式(10)带入式(12)并经代数运算有式(13):
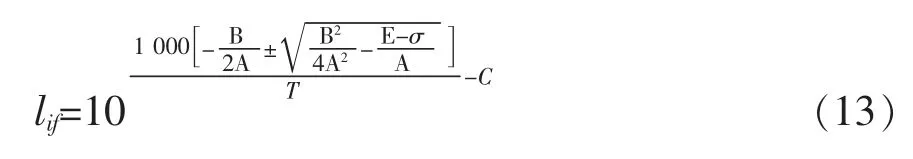
式(13)就是g(t)函数的形式。将式(6),式(7)带入式(13),然后再将式(13)带入式(4)可得第一个大修周期内红套环的累积损伤为式(14):

至此,只要根据有限元计算结果确定h(t),f(t)就可以通过式(14)确定一个大修周期内红套环的寿命损伤。这就是基于拉松-米勒模型的红套环线性蠕变损伤累积模型的详细形式。式(14)中“±”的确定与试验数据的拟合函数有关。根据LMP参数的意义可以确定,当A〉0时取“-”,反之取“+”。
1.3 最大允许大修次数的确定
由于高温蠕变,红套环紧力会持续下降,因此在一段时间后就需要通过调整手段增加红套环的紧力以保证内缸的密封性。增加垫片后红套环紧力增加,并再次进入新一轮的损伤累积过程。为简化模型,假设大修后紧力完全恢复到首次初装紧力,并且材料性质与第一个运行周期内相同。那么在大修后新的运行周期内红套环将与第一个大修周期内有相同的h(t),f(t)和g(t)函数,那么新运行周期内的损伤累积也与第一个运行周期相同。以此类推,经过n个运行周期后总的累积损伤(含第一个周期)为式(15):

当许用损伤为[D]时,保证红套环安全使用的条件是式(16):

至此,只要根据工程经验确定红套环的许用蠕变损伤[D]后就可确定红套环允许的最多大修次数为式(17):
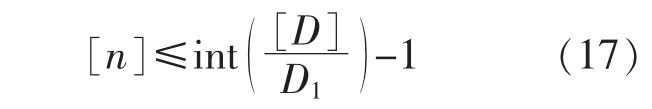
注意,式(17)计算的是允许大修的次数,不含第一次初装在内。int()表示取整。
2 设计实例
某汽轮机高压内缸采用红套环筒形缸结构。最危险红套环工作温度530℃。设计首次大修周期为10万小时。内缸外径1 670 mm,推荐的初始过盈量为:0.835 mm。详细设计阶段发现,0.835 mm的过盈量下长期运行后内缸中分面汽密性不够理想。因此考虑增加过盈量到1.106 5 mm或1.25 mm。常规的强度校核显示各方案下红套环强度均满足要求,汽密性校核显示长期运行后不同过盈量下汽缸的汽密性差异并不显著。现在比较分析3种过盈量下红套环的蠕变损伤累积过程以确定最合理的设计方案。
2.1 第一个大修周期内的损伤累积
该内缸上最危险的红套环工作温度约530℃。保守的假设红套环始终工作在该温度下,即h(t)=530+273.15。式(14)可以进一步简化为仅是f(t)的复合函数。
通过有限元方法可求得不同的过盈量δ下红套环的应力时间曲线如图1所示。从图1可以看出,不同的过盈量下红套环的初始应力差异显著,过盈量1.25 mm时红套环初始应力比过盈量0.835 mm时高约24%。但是经过4万小时松弛后的应力就几乎无差别了。这就解释了不同过盈量,长期运行后密封性基本相当的原因。
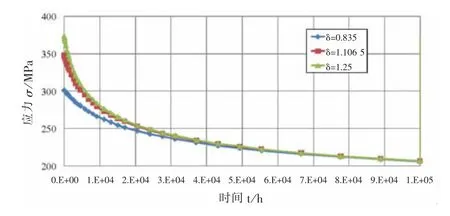
图1 不同过盈量下红套环的应力松弛曲线
拟合图1所示的应力-时间曲线得到f(t)并代入式(14)可求得不同初始过盈量下第一个大修周期(10万小时)内红套环的损伤累积过程。计算结果如图2所示。表1是不同过盈量的详细比较。从图2和表1容易看出不同过盈量下10万小时后红套环的累积损伤差异巨大。红套环预紧量从0.835 mm增加到1.106 5 mm后红套环的初始应力升高了约16%,但是10万小时后的累积蠕变损伤增加了50%。过盈量增加到1.25 mm后,初始应力升高了约24%,但是10万小时后累积蠕变损伤量增加了88%。这表明累积损伤与初始应力之间不是线性关系,初始紧力相对小的增加可能导致累积损伤发生根本变化。
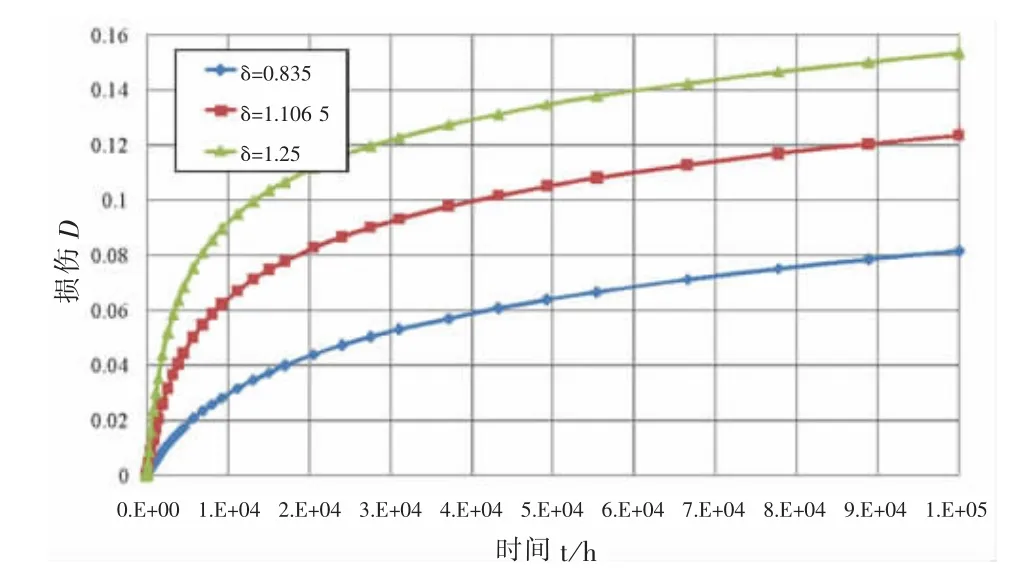
图2 不同过盈量下红套环的损伤累积曲线
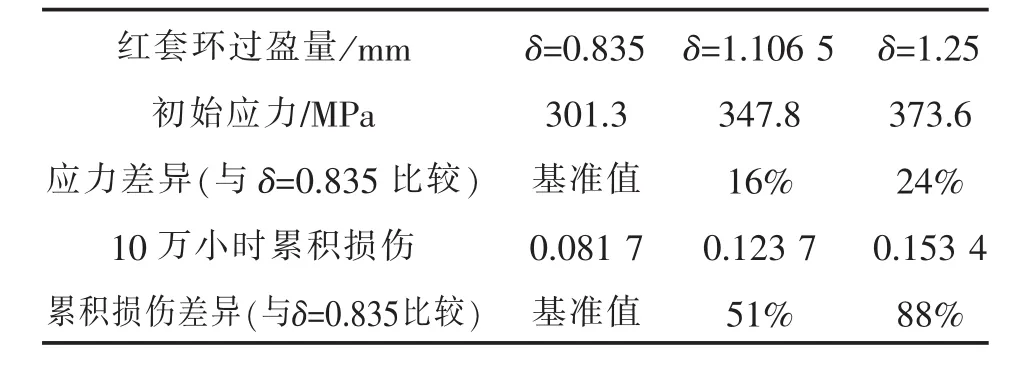
表1 不同初始过盈量下10万小时后红套环的累积损伤
从图2中还可以看出,实际上4万小时后不同初始过盈量下红套环的损伤累积速率基本一致。导致累积损伤显著差异的主要是初始2万小时内的累积损伤。导致该现象的原因与材料的蠕变特性相关。如图3所示为红套环材料530℃时的寿命-应力曲线。从图中可知,材料在373.6 MPa(δ=1.25 mm时的初始应力)应力下的蠕变寿命仅为301.3 MPa(δ=0.835 mm时的初始应力)下的1/7左右。也就是说,在初始阶段,过盈量δ=1.25 mm时的损伤累积速度约为过盈量δ=0.835 mm时的7倍。因此在初始2万小时内不同初始过盈量下红套环应力的差异导致了损伤累积速度的显著差异,从而显著影响全服役期内的损伤累积。
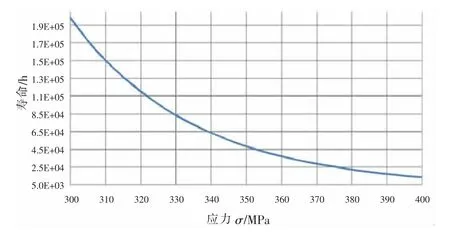
图3 红套环材料不同应力下的寿命-应力曲线(530℃)
由以上分析可见,初始应力较小的差异会导致红套环累积损伤发生显著变化。因此,设计红套环时应避免不必要的过盈量增加。
2.2 红套环的最大允许大修次数
对于上节分析的红套环,其大修周期为10万小时。如前假设,大修后紧力完全恢复到初始紧力,且材料性质保持不变。那么在每个大修周期内红套环的应力和损伤累积曲线相同。作为理论分析,理想的假设[D]=1。按式(17)和表1可确定各方案下红套环允许的最大大修次数如表2所示。

表2 不同方案下红套环的最大允许大修次数
从表中可知,上述红套环过盈量δ=0.835 mm时,红套环允许大修11次。当过盈量δ=1.106 5 mm时,红套环允许大修7次。而当过盈量δ=1.25 mm时红套环允许大修5次。红套环的总使用寿命显著缩短了。单从数据来看,无论哪种过盈量下红套环都具有足够的寿命。但是要注意的是,上述许用损伤按1假设是非常冒进的,同时上述分析没有考虑服役期内疲劳损伤的影响。
2.3 大修周期对蠕变损伤累积的影响
如前所述,在每个运行周期的初始阶段,由于松弛不充分,红套环应力较高。高应力会导致损伤累积速度显著增加。因此不必要的缩短大修周期会导致红套环持续处于高应力状态,其损伤的累积速度也将显著增加。
对于本例,考虑过盈量δ=1.106 5 mm的情况,如图4所示为红套环大修周期分别为5万小时和10万小时时的应力-时间曲线和损伤累积曲线比较。理想的考虑[D]=1,各大修周期下红套环的总使用寿命如图5所示。从图中可知,大修周期为10万小时时红套环可安全使用80万小时,当大修周期为5万小时时红套环的总使用约45万小时,大修周期2万小时时,总使用寿命约24万小时。理论上当检修周期无限短时,红套环应力持续为初装应力347.8 MPa,此时红套环寿命约5.2万小时。
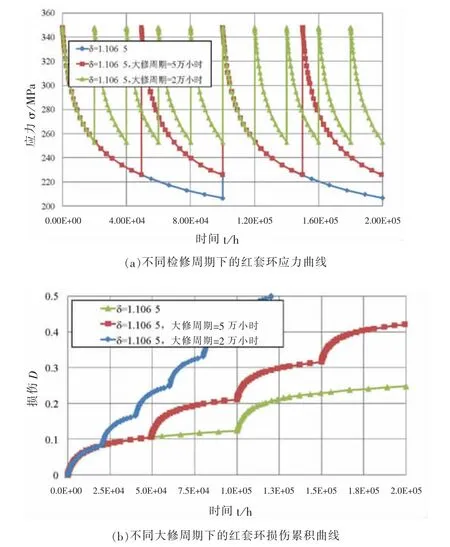
图4 不同大修周期下红套环的应力和损伤累积曲线
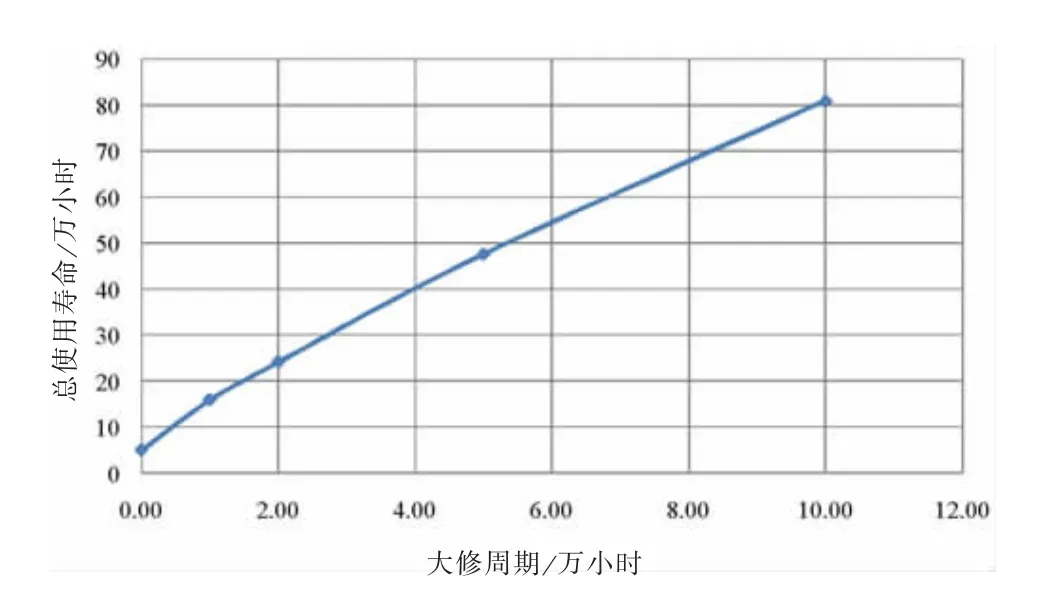
图5 使用寿命-大修周期关系曲线
本计算实例的分析表明,过高的初始紧力会导致红套环的损伤累积速率显著增加,同时还会导致红套环允许大修的次数显著下降。综合考虑汽密性和损伤累积效果后认为过盈量δ=1.106 5 mm的方案更优。
3 总结
本文基于线性损伤理论建立了红套环在服役期内蠕变损伤模型的一般形式,以及基于拉松-米勒蠕变模型时的详细模型,初步建立了红套环允许大修次数的计算方法。对于理解红套环服役期内的性能退化过程和指导工程设计有显著意义。
基于本文创建损伤模型的理论和算例分析表明:
(1)由于蠕变效应,即使增加红套环的初始紧力,红套环的密封紧力也会在较短的时间内下降到和没有刻意增加初始紧力时相近的状态,因此增加红套环的初始紧力并不能长期有效地提高汽缸的密封性;
(2)较小的初始紧力增加可能导致损伤累积速度显著加快,更进一步的,这种影响将显著减少红套环允许大修的次数,从而显著影响红套环的使用寿命和运行维护成本;
(3)不必要的缩短大修周期会导致红套环始终处于较高的应力状态。这将导致红套环持续处于损伤快速累积的状态。从而大大影响红套环的使用寿命。
作为方法研究,本文的分析没有考虑多轴效应的影响。实际红套环处于径向切向应力共同作用的多轴应力状态下,多轴效应必须考虑。另一方面,虽然本文算例中红套环的计算寿命很充足,但是本文中理想的假设许用损伤[D]=1是非常冒进的。最后,本文的分析仅考虑了蠕变损伤累积,实际红套环还要承受疲劳载荷。蠕变和疲劳间有耦合效应这些问题将在以后的工作中进一步研究。
[1]刘东旗,黄果,张晓东,等.大功率汽轮机筒形内缸的强度和汽密性分析[J].东方电气评论,2015,29(2):24-28.
[2]史进渊,孙庆,杨宇,等.大型汽轮机部件蠕变寿命的设计和评估[J].中国电机工程学报,2002,22(3):103-107.
[3]王立滨,荆建平,孙毅,等.损伤力学方法在汽轮机高温蠕变损伤分析中的应用[J].汽轮机技术,2002,44(2):88-90.
[4]刘华锋,王炜哲,蒋浦宁,等.超超临界汽轮机转子蠕变对低周疲劳应变的影响[J].动力工程学报,2010,30(9):715-718.
[5]毛剑峰,王炜哲,张军辉.超超临界汽缸高温强度及多轴蠕变分析[J].力学季刊,2013,34(3):437-443.
[6]吴穹,王炜哲,张军辉,等.超超临界汽轮机中压转子高温蠕变强度分析[J].动力工程学报,2015,35(1):25-29.
[7]徐鸿,郑善合,Karl M.超超临界汽轮机汽缸紧固螺栓高温蠕变断裂研究[J].中国电机工程学报,2007,27(29):80-83.
[8]王争艳,李德华.超超临界汽轮机主汽门阀壳高温蠕变强度分析[J].热力透平,2010,39(4):274-277.
[9]毛剑峰,王炜哲,张军辉,等.汽轮机螺栓松弛对汽缸蠕变强度的影响[J].动力工程学报,2013,33(2):107-111.
[10]航空涡喷、涡扇发动机结构设计准则(研究报告)审定委员会.航空涡喷、涡扇发动机结构设计准则(研究报告):第三册:叶片[R].中国航空工业总公司发动机系统工程局,1997.
[11]闫晓军,聂景旭.涡轮叶片疲劳[M].北京:科学出版社, 2013.
[12]周顺深.火电厂高温部件剩余寿命评估[M].北京:中国电力出版社,2006.
[13]中国动力工程学会.火力发电设备技术手册:第二卷:汽轮机[M].北京:机械工业出版社,2007.
[14]P Singh M,M Lucas G.Blade Design and Anlysis for Steam Turbines[M].McGraw-Hill,2011.
Cumulative Creep Damage Analysis of Cylinder Shrink Ring Based on Linear Damage Theory
Zhao Shizhi,Liu Dongqi,Chen Tiening,Zhang Ming
(Dongfang Turbine Co.,Ltd.,Deyang Sichuan,618000)
The cylinder with shrink ring has been used more and more.With the increasing of the unit parameters,the shrink ring has to work under creep condition.Because of this,during design the initial interference and the maintenance cycle,ensure the safe and reliability of the turbine,the engineers have to consider the creep effect of material.While,the analysis about the shrink ring creep damage is rarely reported.This paper bases on the linear damage theory and the larson-miller method(short as L-M method) to build the general form of the shrink ring creep damage,and studies the effect of the initial interference and maintenance cycle on the creep damage.The conclusion has signification meaning for both understanding the degradation of the shrink ring and guiding engineering design.
steam turbine,shrink ring,creep damage,damage mechanics
TK262
A
1674-9987(2017)02-0036-06
10.13808/j.cnki.issn1674-9987.2017.02.009
赵仕志(1982-),男,工学硕士,工程师,毕业于西安交通大学固体力学专业,现从事汽轮机,燃气轮机的结构、强度和振动设计工作。

