带时间窗的车辆路径问题的精确算法研究

答家瑞，郑澜波

（武汉理工大学 物流工程学院，湖北 武汉 430063）

带时间窗的车辆路径问题的精确算法研究

答家瑞，郑澜波

（武汉理工大学 物流工程学院，湖北 武汉 430063）

将CVRP（Capacitated Vehicle Routing Problem）中的二维车流模型扩展至VRPTW中，用它来替代列生成算法中的分支-切割过程，为解决VRPTW提供了一种新思路。同时对最少车辆数量的理论上界进行了猜想，并用Solomon基准测试包进行了实验，求解出的算例均肯定了这一猜想。

时间窗；车辆路径问题；运筹学；整数线性规划；列生成；精确算法

1 引言

带时间窗的车辆路径问题（Vehicle Routing Problem with Time Windows，VRPTW）是对车辆路径问题的扩展，最早由Pullen在1967年提出[1]，其主要不同点在于添加了一个时间窗来限制每个客户地点的服务时间，该限制可以针对于客户服务的最早开始时间、车辆停留在客户点的最短时间以及客户服务的最晚开始时间等，这些限制统称为时间窗约束。

VRPTW可以定义为一组车辆(V)，一些客户(C)和一个有向图(G)。该有向图中包括|C|+2个点，其中客户点用1，2，…，n表示，仓库点用点0（开始点）和n+1（结束点）表示。用N来表示所有点的集合，A表示所有边的集合，即G(N,A) 。对于每条边（i，j），cij表示该边上的行驶成本，tij表示途经该边的行驶时间。对于每个客户点i都有一个时间窗[ai,bi]，即到达i点的车辆最早开始服务时间为ai，最晚开始服务时间为bi，每个点的服务时间长度为sti，需要装载的货物重量（容量）为di。对于每辆车都有一个相同的载重量（最大容量）q。

2 列生成算法

列生成（Column generation）[2]是一种求解大规模整数线性规划的方法。使用它进行求解时，不需要用到原始问题中所有的变量，而是求解一个子集（subset）。具体来说列生成通常会产生一个主问题，这个主问题的解依赖于一个或多个子问题的多重解（repeated solution）。

接下来用数学的方法来描述，我们用线性规划的方法定义主问题（master problem，MP），数学模型如下：

目标函数：

约束条件：

这是一个通用的线性规划模型，其中集合J代表所有的列（column）。MP的对偶变量用非负向量π来表示，根据对偶理论，我们希望找到一个 j∈J能够使得：=cj-πtaj的值最小。当 ||J的值很大时，这种直接定价（pricing）的方法运算成本很高。所以我们考虑取一个合理的子集 j'∈J来操作，用间接枚举（implicit enumeration）的方法来计算检验成本（reduced cost），它被称为限制主问题（restricted master problem，RMP）。假设λ和π分别是当前RMP的原始最优解和对偶最优解，给定一个集合A，它由列（column）aj,j∈J组成，目标函数的成本系数cj可以通过关于aj的函数式c计算得到，由此得到子问题的修改成本：

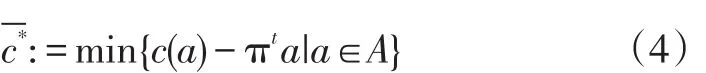
带时间窗的车辆路径问题（VRPTW）可以用集合划分问题（Set-partitioning problem）的模型来构造[3]。用P来表示所有可能的路径集合（其中的所有路径均满足时间窗与容量约束），对于每条路径p∈P，cp表示路径p的行驶成本，对于每个客户点i，当路径p访问了客户点i则aip取值为1，否则取值为0。定义路径变量Yp，代表该路径是否在最优路径上，如果路径p在最优路径中则Yp=1，若不在则取0。数学模型如下：

目标函数：

约束条件：

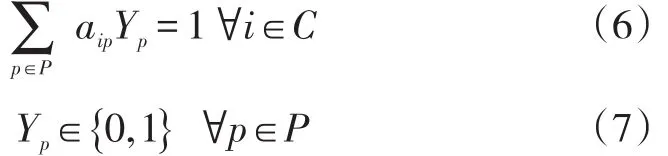
目标函数（5）所有路径的总成本最小。集合划分约束（6）保证了每个客户点刚好被一辆车访问一次。

对约束条件（7）进行线性松弛，使Yp∈R，得到：

将约束条件（8）替代（7）加入到主问题模型中，就得到了线性主问题的线性模型。此时，变量Yp代表每条路径p的权重，约束条件（6）等式左侧用矩阵的方式描述可以表示为：每一列代表一条可行路径乘以权重Yp，每一行代表一个客户点乘以权重Yp。

基于列生成的理论，可以得到限制主问题的数学模型：

目标函数：

约束条件：

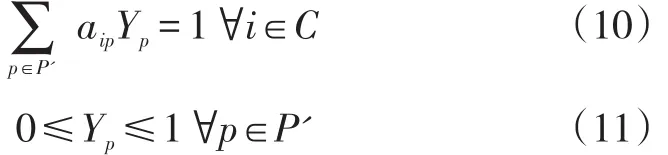
集合P'⊆P，仅包含所有已经生产的路径。限制主问题（RMP）的初始解我们选择所有只含有一个客户点的路径，即路径0→i→n+1（i∈C），此时约束条件（6）等式左侧的矩阵为单位矩阵。

算法主要思路如下：首先对主问题进行线性松弛，得到原始的限制主问题。接着将初始解放入限制主问题后，对其用单纯形法求解，同时生成每个客户点的对偶变量（π）并求得其值。接着对子问题目标函数中的路线行驶成本进行修改是边（i，j）上修改后的成本，=cij-(πi+πj)/2，并求解子问题，子问题的解值称为检验成本（reduced cost），解（solution）可以构成一条新的路径。如果检验成本为负数（negative reduced cost），则将新的路径作为一列（column）加入到限制主问题（restricted master problem）当中，重新求解，生成新的对偶变量，如此循环直到检验成本非负。最后对主问题进行求解，若可以求得整数解，则该解为最优解；若求得不为整数解，则该值为此问题的下界，接着用分支-切割法进行求解，重复上述循环直到求得最优解。

3 基于二维车流的数学模型

传统的带容量约束的车辆路径问题（Capacitated VRP，CVRP）的数学模型十分丰富，但由于时间窗的约束，能够应用到VRPTW的数学模型很少，主要是因为时间窗的约束难以和传统的容量-子回路消除约束相结合。我们尝试着将CVRP的经典二维车流模型加以改进，演变为适用于VRPTW的数学模型。

首先介绍传统的容量-子回路消除约束，以下描述中出现的变量与参数均与前文叙述一致。给定一个集合W⊆C，定义r(W)代表W集合中能够服务所有客户点并满足车辆容量约束的最小车辆数，定义，代表W集合中的所有货物总重量。根据装箱问题（Bin Packing Problem，BPP）的理论研究，r(W)的上界（upper bound）为d(W)/q（向上取整），凭借对CVRP整数规划模型的多面体结构分析，学者们将该上界提高到2d(W)/q（向上取整）。基于此，引出两个重要的约束条件，容量切割约束（Capacity-Cut Constraints，CCCs）：

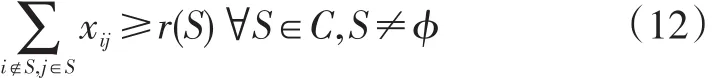
与通用子回路消除约束（Generalized Subtour Elimination Constraints,GSECs）：

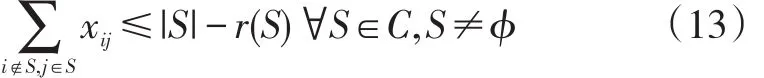
可以看出这类约束在模型中的个数是指数级的，需要用分离（separation）的算法来寻找违反约束条件的集合，加入时间窗约束后，分离问题变得更加复杂，难以快速得到所需子集。由于理论上界研究的突破，应用这类约束处理CVRP十分有效，但该下界无法应用在VRPTW中。

在VRPTW中得出类似r(W)的下界，即W集合中能够服务所有客户点并满足车辆容量约束和时间窗约束的最小车辆数目十分困难，所以我们考虑使用1960年Miller，Tucker和Zemlin对非对称旅行商问题（ATSP）进行子回路消除的思路进行处理（简称MTZ）。引入一个额外变量ui∈R,i∈C，MTZ的约束可表述为：

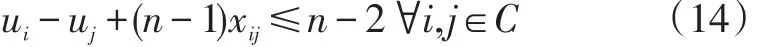
不难看出经典的三维多商品网络流模型中的时间窗约束就是由MTZ演变而来。1990年Desrochers和Laporte对MTZ进行了增强，提出了新的约束条件（简称DL）：

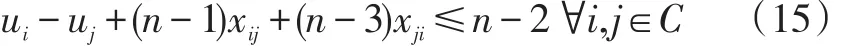
这种构造保证了当xij=1时，ui+1=uj，从而使得其多面体结构更小。

我们将这种思路应用在容量-子回路消除约束中，提出新的数学模型，其中定义K是所需车辆的数量，即路径数量，模型如下：

目标函数：

约束条件：

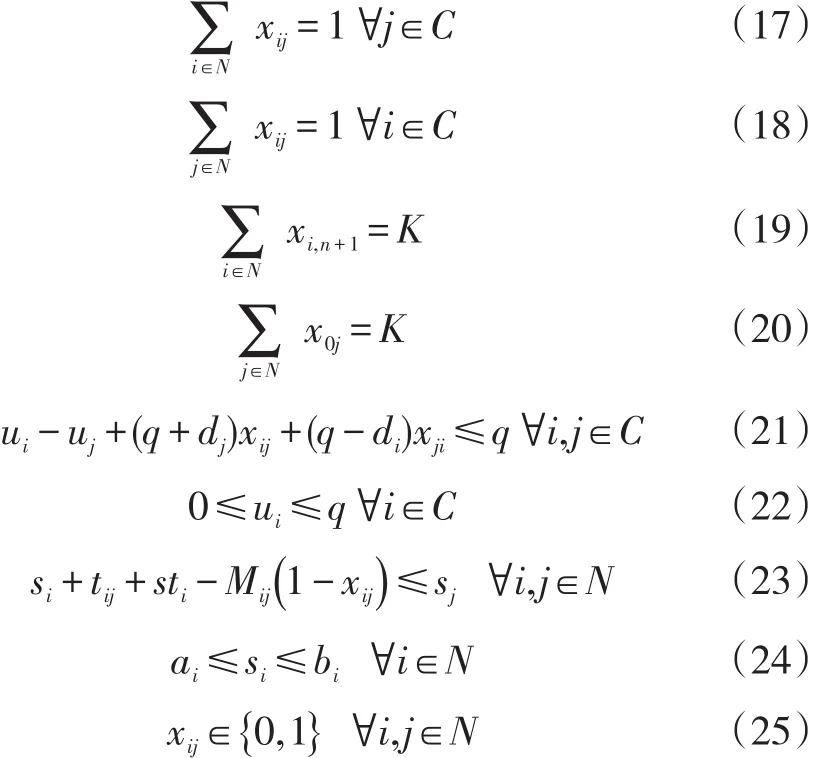
目标函数（5）同样是求总行驶路程最短。入度（indegree）和出度（outdegree）约束条件（17）和（18）保证每个客户点进入的边数与离开的边数均为1；（19）与（20）保证了从仓库点0出发的车辆数与到达仓库点n+1的车辆数就是图中的路径数量；（21）和（22）确保了容量约束的满足；（23）与（24）确保了时间窗约束的满足，其中Mij通常代表一个非常大的常数，在该问题中它的值可以减少为

该模型相比于经典的三维多商品网络流模型[4]，整数变量x减少了一维，但增加了一个线性变量u。提升该模型计算性能的关键在于如何降低K的上界，即至少需要多少辆车可以形成最优路径。在利用列生成算法解决基于集合划分的数学模型时，会得到线性主问题的下界（检验成本为0时），同时产生线性解中的路径数量值K'（该数量值可能不是整数），我们认为K'（向上取整）或K'+1（向上取整）很有可能就是K的理论上界，所以用该模型来替代列生成算法中得到主问题线性最优解后的分支-切割过程，以测试模型质量与最优性。

4 带资源约束的基本最短路径问题

带资源约束的基本最短路径问题（Elementary Shortest Path Problem with Resource Constraints,ESPPRC）是VRPTW基于列生成算法的子问题。当用集合划分模型作为主问题，利用列生成算法来解决VRPTW时，子问题被分解成多个性质相同的ESPPRC。更加明确地来说，子问题是一个带时间窗与容量约束的基本最短路径问题（Elementary Shortest Path Problem with Time Windows and Capacity Constraints，ESPPTWCC），其中“基本”（elementary）的意思是每个客户点只能出现一次，即最优解中不存在回路（cycle）[5]。

本文基于整数线性规划，加入以下三组有效不等式对子问题进行了建模求解。

4.1 点边不等式

定义集合M⊆N，给出不等式：

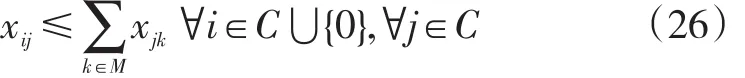
M集合仅包含同时满足以下两个条件的点k。i→j→k是可行路径，即在时间窗和容量约束下车辆能够按顺序依次访问点i，j，k；边（i，j）、（j，k）与（i，k）的修改后成本满足

4.2 时间前后不等式

如果i点在时间窗约束下不能到达j点，即ai-bj+sti+tij＞0时，则i点只能在j点访问后再进行访问或者不访问。当ai-bj-stj-tji≤0时，时间前后不等式可以表述为：

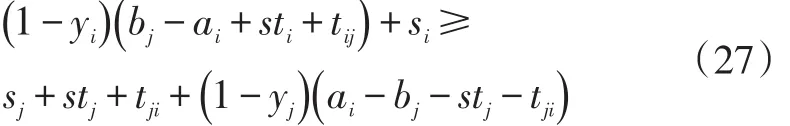
4.3 顺序前后不等式

对任意客户点i，定义两组集合Pre,Suc⊆N，描述如下：

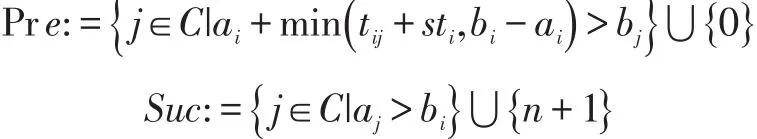
Pre代表一些只能出现在i点之前的点，Suc代表一些只能出现在i点之后的点。

考虑所有从集合Pre中出发到集合Suc的路径，如果点i在最短路径上，则该路径一定会经过i点，故顺序前后不等式如下：

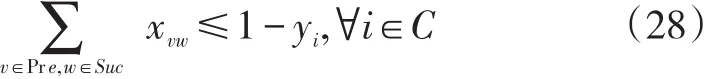
5 实验结果

实验数据来自于经典的Solomon基准测试包[3]，测试包中的数据集合分为三类，

r组：客户点坐标呈随机分布；

c组：客户点坐标呈现分块聚集分布；

rc组：客户点坐标既有随机分布又有分块聚集分布。

每个算例都包括100个客户点、50个客户点和25个客户点三种规模，后两种分别是取包括100个客户点的完整算例中的前50个和25个客户点。

计算实验都是在含有2.5GHz的Intel（i7-4710MQ）处理器、12GB内存以及配有64位Windows操作系统的戴尔一体机上运行。使用Java（编译版本1.7）在Eclipse上进行算法编译，借助IBM Ilog Cplex/Concert 12.6进行建模优化。

主问题：基于集合划分的数学模型；

子问题：加入三种有效不等式后的整数线性规划模型。

得到主问题的下界后用基于二维车流的数学模型求最优解，该方法简称为ILP算法。

ILP算法是通过在Ilog Cplex中的Cplex优化器上建立列生成结构与数学模型进行求解，Cplex参数设置为默认。

实验在求解完所有子问题得到主问题的下界后，会得到一个线性解中的路径数量值K'，我们将二维车流模型中的K（所需的车辆数量或路径数量）定义为整数变量，其取值范围设置为[K ',K'+1]，直接求解该模型，输出最优解。为了测试修改后二维车流模型的性能，我们不会将下界加入到模型中去。

目前Solomon基准测试包对于我们的算法过于困难，仅选择其中25个客户点的数据进行测试，以验证修改后的二维车流模型的性能。

表中具体说明如下：

LB：下界（Lower Bound），空白格代表500秒内未求解出下界；

Opt：最优解（Opimal solution），空白格代表500秒内未求解出最优解；

Num：子问题的迭代次数，即求解了Num个子问题；

Paths：产生的路径数量之和，即加入到主问题中列（column）的数量；

LBT：求解到下界的时间，单位是s；

OptT：修改后二维车流模型的求解时间，单位是s；

TT：总时间（Total Time）。

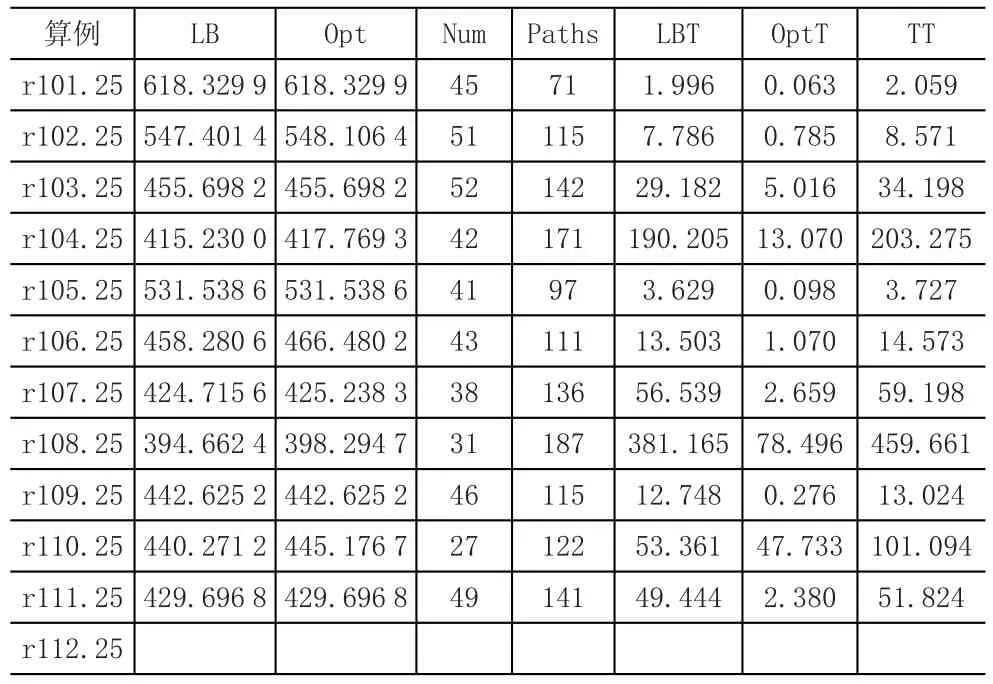
表1 r组25个点的VRPTW测试结果

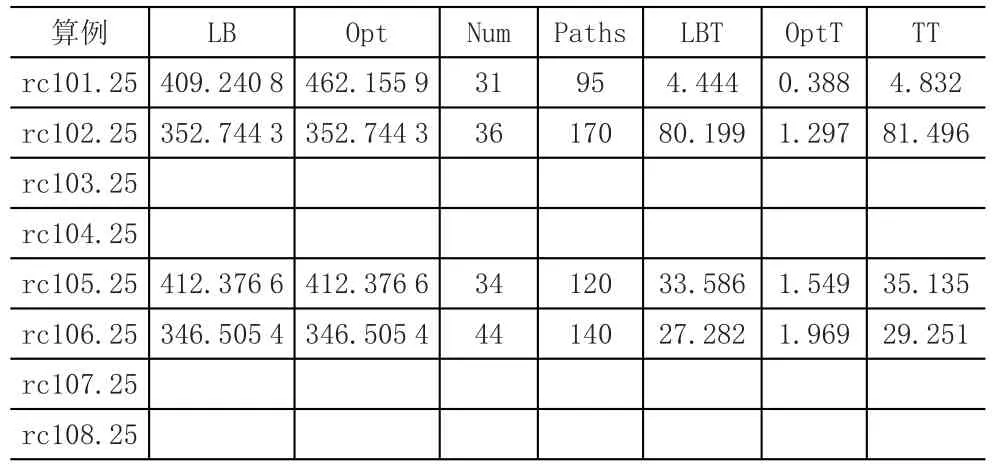
表2 rc组25个点的VRPTW测试结果

在表1、表2和表3中，可以看出在求解出下界后，用修改后的二维车流模型来求解得最优解的时间（OptT）非常短，可以认为它能够替代列生成算法后期的分支-定界部分。在目前求解出的所有算例中，二维车流模型的解与前人提供的最优解相同，但由于尚未求解出更多的算例，无法肯定K'+1（向上取整）就是K（最优解中的路径数量）的理论上界，目前的结果都倾向于肯定这一猜想。

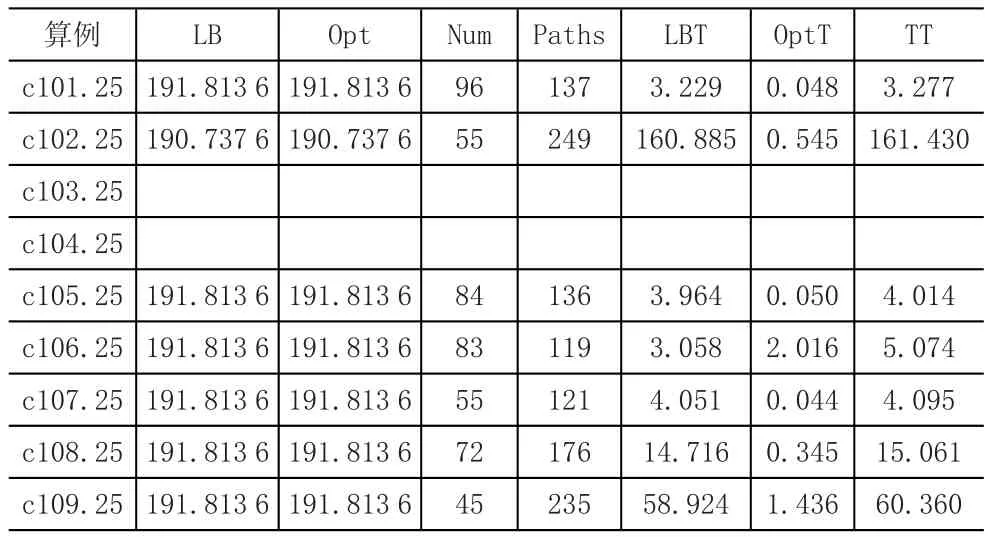
表3 c组25个点的VRPTW测试结果

6 结束语

带时间窗的车辆路径问题是经典的组合优化问题，也是目前应用最广泛的运输问题之一，具有很高的研究价值。国内的研究往往倾向于用启发式方法解决该问题，精确算法的研究非常匮乏。对于启发式方法，我们认为它最大的优势在于高效性和通用性，而这也在一定程度上导致了它精确性的不足。针对一个NP-hard问题，如果没有透彻的理论分析和精确算法做支撑，就很难建立适合的启发式算法，更不能保证其求解质量。

我们将CVRP中的二维车流模型扩展至VRPTW中，用它来替代列生成算法中得到主问题线性最优解后的分支-切割过程，为解决VRPTW提供了一种新思路。

[1]Pullen H G M,Webb M H J.A Computer Application to a Transport Scheduling Problem[J].Computer Journal,1967,10(1).

[2]Danzig G B,Wolfe P.The decomposition algorithm for linear programming[J].Econometrica,1961,(4)：767-778.

[3]Desrochers M,Desrosiers J,Solomon M.A new optimization algorithm for the vehicle routing problem with time windows[J].Operations research,1992,40(2)：342-354.

[4]Toth P,Vigo D.The vehicle routing problem[M].Beijing：Tsinghua University Press,2011.

[5]Jepsen M K,Petersen B,Spoorendonk S,et al.A branch-andcut algorithm for the capacitated profitable tour problem[J].Discrete Optimization,2014,14(C)：78-96.

Study on Exact Algorithm for Vehicle Routing Problem with Time Window

Da Jiarui,Zheng Lanbo
(School of Logistics Engineering,Wuhan University of Technology,Wuhan 430063,China)

In this paper,we extended the 2D car flow model from the capacitated vehicle routing problem(CVRP)to the vehicle routing problem with time window(VRPTW)to replace the branch-and-cut process of the column generation algorithm and provide a new line of thinking for the solution of the VRPTW.At the same time,we hypothesized the theoretical upper bound of the minimal vehicle quantity and tested and verified it using the Solomon benchmark test package.

time window;vehicle routing problem;operations research;integer linear programming;column generation;exact algorithm

F224.0

A

1005-152X(2017)06-0095-05

10.3969/j.issn.1005-152X.2017.06.023

2017-05-01

国家自然科学基金（71501152）

答家瑞（1992-），男，湖北武汉人，硕士研究生，研究方向：运筹学与供应链网络；郑澜波（1980-），女，武汉理工大学副教授，博士，研究方向：运筹学与供应链网络。