边界质量对覆冰输电线舞动的影响分析

游溢+李朋+李文胜+何成

摘 要：基于曲梁理论、Hamilton原理和伽辽金方法，建立同时考虑相邻跨刚度以及绝缘子串质量作用下的覆冰输电线三自由度舞动运动方程。采用Mathematica数学软件编制三自由度曲梁模型对覆冰输电线舞动进行求解分析，分析结果表明，随着边界绝缘子串质量的增大，覆冰输电线竖向的舞动幅值会变大，而侧向和扭转向的舞动幅值则会减小。此外，发生舞动的临界风速也相应增大，整体结构相对更稳定。

关键词：曲梁理论；覆冰输电线；舞动；边界质量

中图分类号：TM726 文献标志码：A 文章编号：2095-2945（2017）19-0188-02

引言

当自然风绕过非圆形截面的导线时将产生持续时间长的大幅自激振动，即输电线舞动。该大幅的振动会破坏输电线路，甚至造成供电系统的瘫痪，因此对于覆冰输电线舞动的研究和防治是一项意义重大的任务[1-6]。

为了解决输电线自身的抗弯刚度对舞动的影响，在zhu[7]的研究基础上，Luongo[8]建立了三自由度曲梁模型，同时将竖向、侧向和扭转向运动考虑进去。并进行了覆冰输电线的非线性舞动分析，结果表明，考虑输电线自身的刚度后，计算结果与实际情况更吻合，但该模型并未考虑覆冰输电线截面的偏心。近来，颜志淼[9]推导了考虑输电线偏心作用的三自由度（竖直方向、水平方向、扭转方向）舞动模型，该模型的建立得益于zhu[7]的曲梁理论和Masson[10]的迁移坐标系理论的相互结合。接着，霍涛[11]完善了颜志淼的模型，将相邻跨和绝缘子串对覆冰输电线的作用简化为输电线舞动模型的线性弹簧边界。

本文在基于颜志淼[9]、霍涛[11]提出的考虑覆冰输电线偏心的三自由度舞动力学模型的基础上，研究分析绝缘子串质量对覆冰输电线舞动的影响。

1 考虑边界条件的输电线曲梁模型

考虑输电导线相邻跨和绝缘子串对其的影响分别简化为输电导线边界的刚度和质量条件，如图1所示。

根据变分原理，覆冰输电导线的运动方程可以表示为：

与霍涛[11]文中不同的是，由于考虑了绝缘子串的动能，体系的总动能应表示为：

将覆冰输电线拉格朗日应变-位移关系以代入公式（1）得到考虑边界条件的覆冰输电导线6自由度舞动方程：

利用自由度缩减原理，对MT和KT矩阵进行自由度缩减

其中，M1，M2，M3，M4，K1，K2，K3，K4为3×3刚度矩阵。

因此，同时考虑边界刚度和边界质量的覆冰导线6自由度舞动方程将缩减为3自由度舞动方程：

详细的过程参照颜志淼[9]、霍涛[11]文中所述。

2 边界质量对舞动的影响

当同时考虑相邻跨刚度和绝缘子串的质量对覆冰舞动的影响以后，会对风速舞动幅值和上下临界风速产生影响，下面分别对这几种影响进行分析。

如图2所示，固定边界三自由度曲梁模型Model 1和考虑边界弹性刚度和边界质量的曲梁Model 2的对比分析表明，随着风速的增大，三个方向的振动幅值均是先增大再减小，直至为零。此外，与边界固定条件相比，同时考虑相邻跨的刚度和绝缘子串质量之后，输电导线的竖向以及侧向舞动幅值均有不同程度的减小，而扭转方向的舞动幅值则增大。

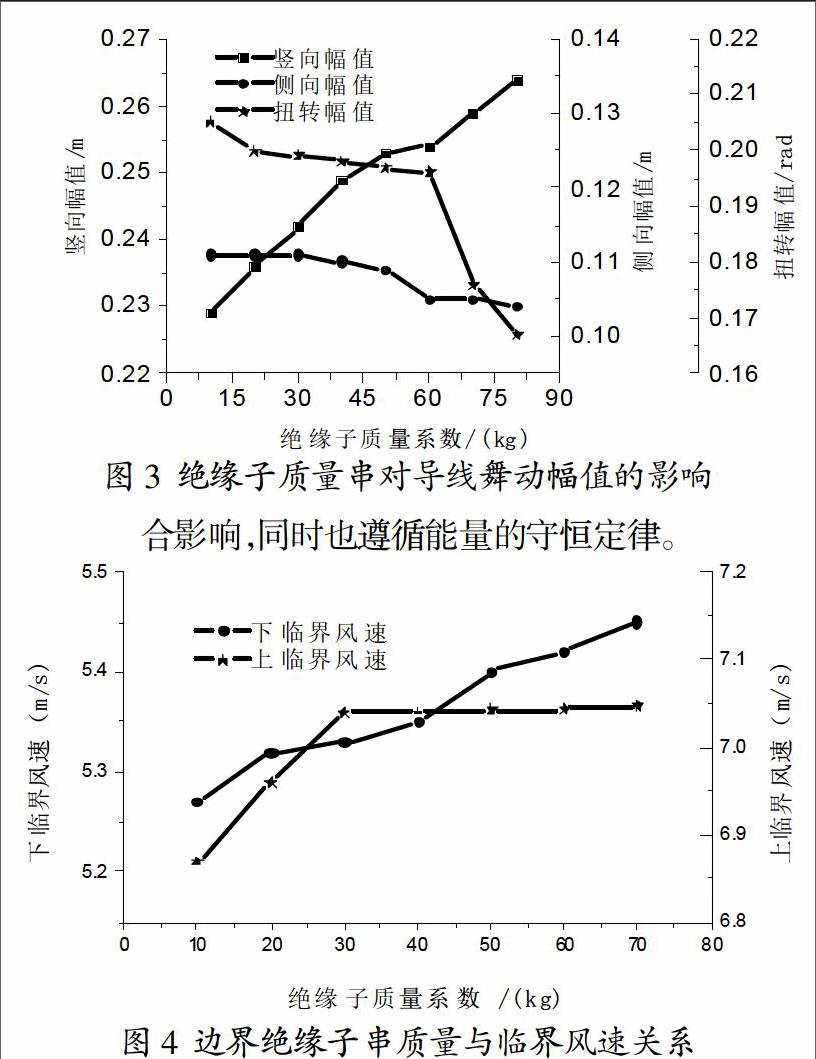
图3结果表明：随着绝缘子质量的增大，竖向舞动幅值变大，侧向和扭转舞动幅值减小，这是也刚好满足三个运动方向相互耦合影响，同时也遵循能量的守恒定律。

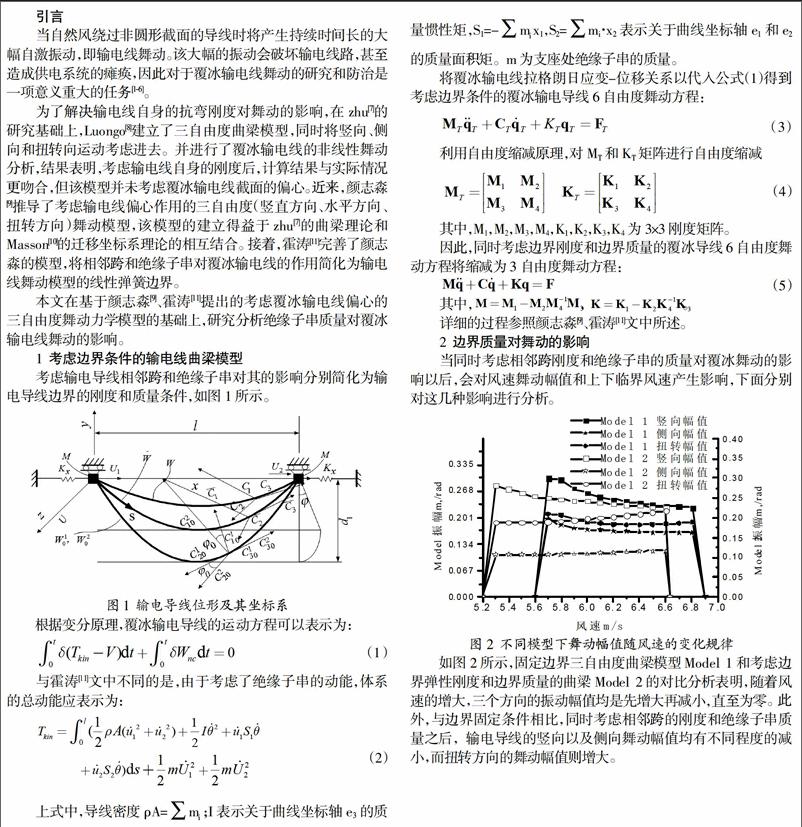
如图4所示：当绝缘子质量变大，舞动发生的上下临界风速也相应增大；由此可见，增大绝缘子串的质量越小可以结构越稳定，发生舞动的概率越小。

3 结束语

基于曲梁理论、哈密顿原理以及伽辽金方法建立了三自由度覆冰输电线的舞动模型，利用Mathematica软件编制程序对覆冰输电线的舞动规律，相邻跨和绝缘子串质量对舞动的影响进行求解分析，结果表明：随着风速的增大，三方向的舞动幅值均从零逐渐增大最后又逐渐减小至零；此外，当绝缘子质量的增大，竖向舞动幅值增大，而侧向和扭转舞动幅值则减小，且发生舞动的上下临界风速也增大，从而整体结构相对更为稳定，这一结论可为实际工程提供参考。

参考文献：

[1]蒋兴良，易辉.输电线路覆冰及防护[M].中国电力出版社，2002.

[2]马建国.三峡输电工程防导线舞动的探讨[J].华中电力，1998（02）：47-50.

[3]张鸣，陈雄波.架空輸电线路导线舞动机理及防舞动研究[J].湖北电力，2008（01）：43-44.

[4]赵作利.输电线路导线舞动及其防治[J].高电压技术，2004（02）：56-58.

[5]朱宽军，尤传永，赵渊如.输电线路舞动的研究与治理[J].电力建设，2004（12）：18-20.

[6]蒋兴良，周仿荣，王少华，等.输电导线覆冰舞动机理及防治措施[J].电力建设，2008（09）：14-15.

[7]Z.H. Zhu，S.A. Meguid. Vibration analysis of a new curved beam element[J]. Journal of Sound and Vibration，2008，309（1-2）：86-95.

[8]A. Luongo， D. Zulli， G. Piccardo. A Linear Curved-Beam Model for the Analysis of Galloping in Suspended Cables[J]. Journal of Mechanics of Materials and Structures， 2007，2（4）：675-694.

[9]Z. M. Yan， Z. T. Yan， Z. L. Li， T. Tan. Nonlinear galloping of internally resonant iced transmission lines.considering eccentricity [J]. Journal of Sound and Vibration， 2012，331（15）：3399-3616.

[10]J. Mason. Variational Incremental and Energy Methods in Solid Mechanics and Shell Theory[M]. Elsevier Scientific Publishing Company，1980.

[11]霍涛，晏致涛，李正良，等.考虑弹性边界条件曲梁模型的覆冰导线舞动[J].振动与冲击，2013，32（21）：85-91.