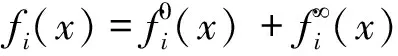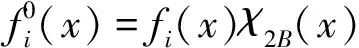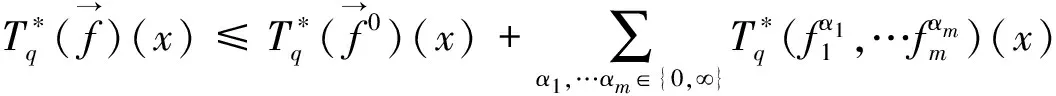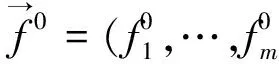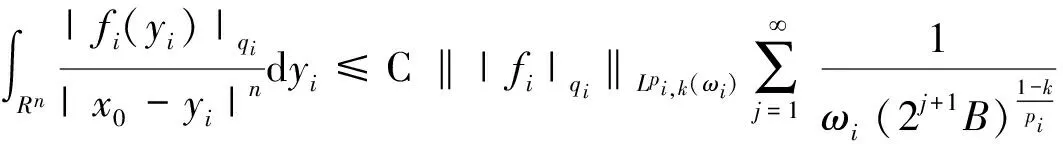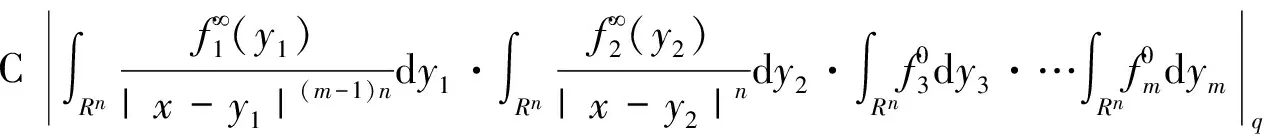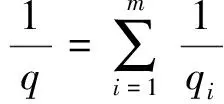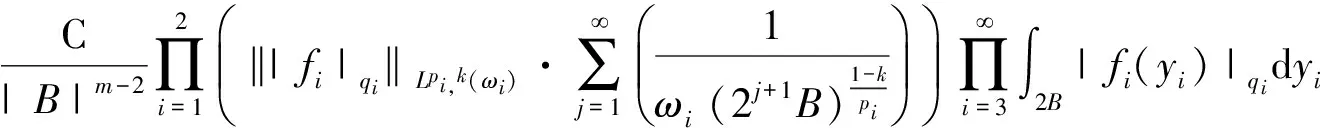向量值多线性极大奇异积分算子的有界性研究
张慧慧, 骆雯琦
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
向量值多线性极大奇异积分算子的有界性研究
张慧慧, 骆雯琦
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
利用一类多线性反Hölder不等式,得到了向量值多线性极大奇异积分算子在加权Morrey空间中的有界性。
向量值多线性极大奇异积分;加权Morrey空间;矢量权;多线性反Hölder不等式
1 引言及主要结论
众所周知,多线性算子理论在调和分析的研究中起着重要的作用。2002年Grafakos和Torres[1]系统地研究了如下形式的多线性奇异积分算子:
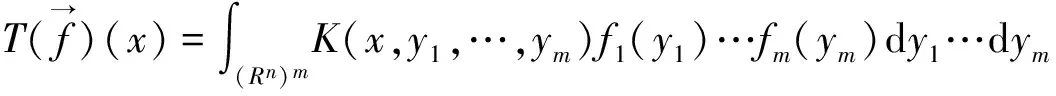
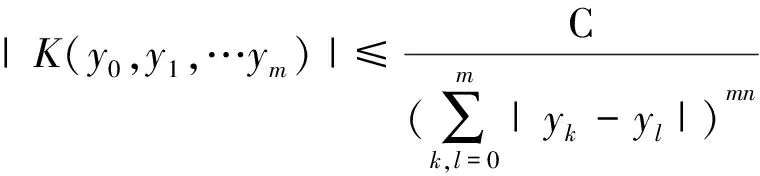
(1)

(2)
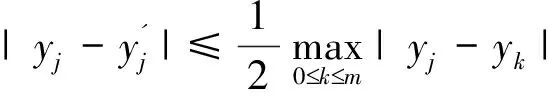
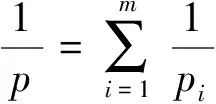
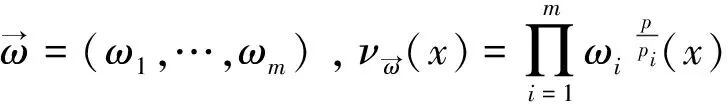
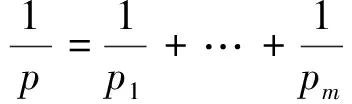
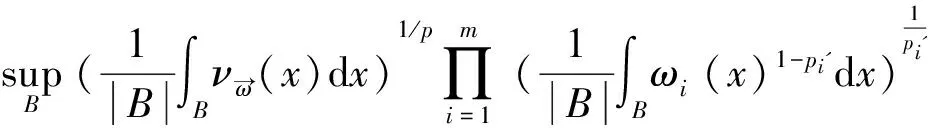
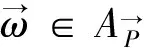


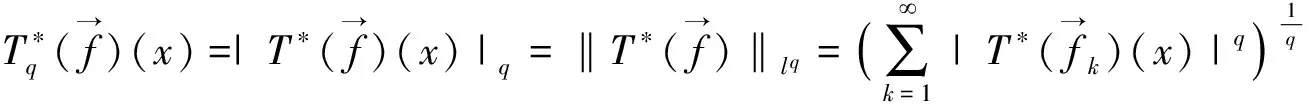

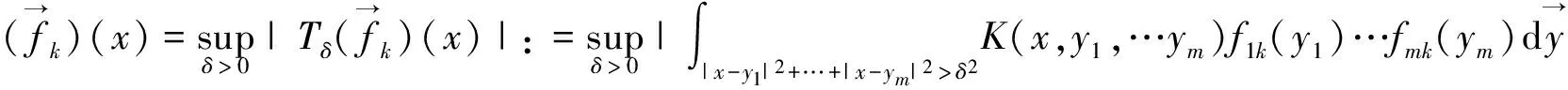
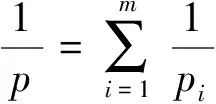
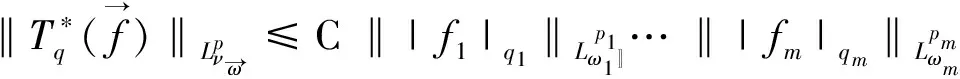
(3)
上世纪30年代,Morrey[4]通过引入著名的 Morrey空间Mp,λ(Rn)来研究二阶椭圆微分方程局部解问题,这里Mp,λ(Rn)的定义为

其中0≤λ 2009年,Komori以及Sharai[5]首次引入了加权Morrey空间Lp,k(ω),其定义为 在给出本文主要结论之前,先介绍AP权函数类的定义。 定义1.2[7]假设ω(x)是一个非负局部可积函数,若对所有的边长与坐标轴平行的方体Q,均有 其中1 根据Hölder不等式,可得Ap⊂Aq(1 本文主要结论如下: 在给出定理1.1的证明之前,我们先给出一些证明过程中需要的引理。 对任一方体B,如果ω满足ω(2B)≤Cω(B),其中C为和ω以及B无关的常数,则我们称ω满足二倍测度条件,记为ω∈Δ2。 引理2.1[8]如果ω∈Ap(1 引理2.2[8]如果ω∈Δ2,则存在大于1的常数C,使得ω(2B)≥Cω(B)。 引理2.3[9](多线性反Höolder不等式)如果ωi∈Ar,其中r为大于1的任意实数,则对任意的方体 B⊂Rn,存在一个和方体B无关的常数C,使得 根据引理2.3,我们可得如果ωi∈Api,则有 (4) (5) |yi-x0|<2|x-yi|。然后类似于文献[5]第226页中的相关方法,我们有 (6) 故根据引理2.1和2.2,可得 (7) α1=α2=,α3=α4=…=αm=0这种情形,因为其余的情形计算过程都是类似的。首先根据(1),我们有 接下来给出∫2B|fi(yi)|qidyi的估计。注意到ωi∈Api,根据Api权函数类的定义(定义1.2)以及Hölder不等式,可得 (8) 再次利用引理2.1和2.2以及(7),可得 (9) 综合(5)(8)以及(9),根据加权Morrey空间Lp,k的定义,我们完成了定理1.1的证明。 [1] GRAFAKOS L,TORRES R.Multilinear Calderon-Zygmund theory[J].Adv Math,2002,165:124-164. [2] LERNER A,OMBROSI S,PEREZ C,et al.New maximal functions and multiple weights for the multilinear Calderon-Zygmund theory[J].Adv Math,2009,220:1222-1264. [3] SI Z,XUE Q.Weighted estimates for commutators of vector-valued maximal multilinear operators[J].Nonlinear Anal,2014,96:96-108. [4] MORREY C.On the solutions of quasi-linear elliptic partial differential euqations[J].Trans Amer Math Soc,1938,43:126-166. [5] KOMORI Y,SHIRAI S.Weighted Morrey spaces and a singular integral operator[J].Math Nachr,2009,282:219-231. [6] WANG H,YI W.Multilinear singular and fractional integral operators on weighted Morrey spaces[J/OL].J Funct Spaces Appl,Vol 2013,2013:Article ID735795[2017-02-28].https://www.hindawi.com/journals/jfs/2013/735795/. [7] MUCKENHOUPT B.Weighted norm inequalities for the Hardy maximal function[J].Trans Amer Math Soc,1972,165:207-226. [8] GRAFAKOS L.Classical and Modern Fourier Analysis[M].New Jersey:Prentice Hall,2004:135-136. [9] XUE Q,YAN J.Multilinear version of reversed Hölder inequality and its applications to multilinear Calderon-Zygmund operators[J].J Math Soc Japan,2012,64:1053-1069. The Research for the Boundedness of the Vector-valued Multilinear Maximal Singular Integral Operators ZHANG Huihui, LUO Wenqi (School of Mathematics and Computer Science, Shangrao Normal University,Shangrao Jiangxi 334001, China) By using the multilinear reversed Hölder inequality,we prove the boundedness of the vector-valued multilinear maximal singular integrals on the weighted Morrey space. vector-valued multilinear maximal singular integrals; weighted Morrey space; multiple weight; multilinear reversed Hölder inequality 2017-03-13 国家自然科学基金(11561057,11226104);江西省自然科学基金(20151BAB211002);江西省教育厅科技项目(GJJ151054);上饶师范学院校级课题(201401) 张慧慧(1985-),女,河南沈丘人,讲师,硕士,研究方向为调和分析。E-mail:zhanghuihuinb@163.com O177.2 A 1004-2237(2017)03-0017-05 10.3969/j.issn.1004-2237.2017.03.004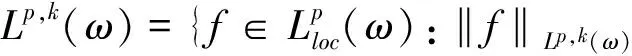
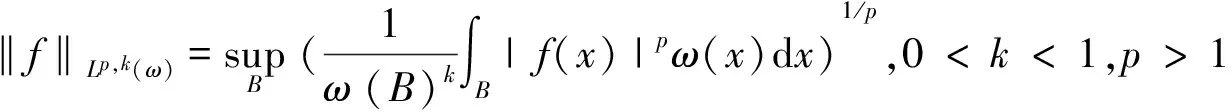
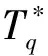
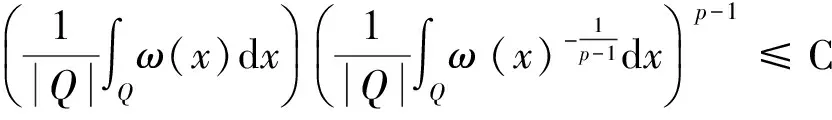
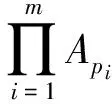
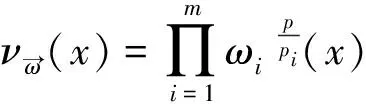
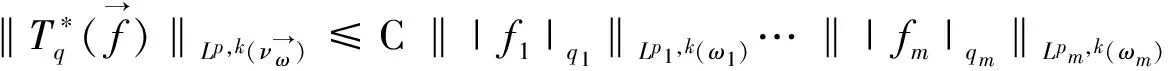
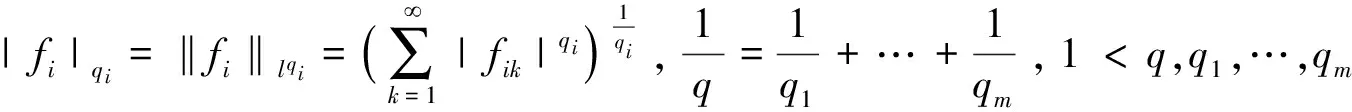
2 本文主要引理
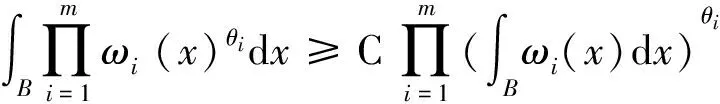
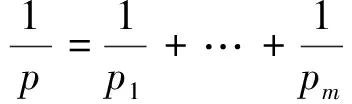
3 定理1.1的证明