可伴算子保持Hilbert C*-模中g-框架的充要条件
相中启,喻晓,袁邓彬,黄飞鸿
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
可伴算子保持HilbertC*-模中g-框架的充要条件
相中启,喻晓,袁邓彬,黄飞鸿
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
利用算子理论方法证明了可伴算子保持HilbertC*-模中的g-框架当且仅当它是单射且有闭的值域,这修正了已有的一个结果。
HilbertC*-模;g-框架;可伴算子;闭值域
Hilbert空间中的框架 (经典框架) 是规范正交基的推广,它由Duffin和Schaeffer[1]于1952年引入,当时被用于处理非调和Fourier级数中的一些深刻问题。1986年,Daubechies等[2]的突破性工作奠定了框架理论在小波分析中的重要地位。目前,框架作为一个重要工具已被广泛应用于信号编码、图像和数据处理、抽样理论等方面[3-5]。一些研究者将框架概念进行离散推广,于是产生了多种广义框架形式,Sun W C将已有的几种框架作统一讨论,提出了g-框架的概念[6]。
近些年来,一些学者将框架和g-框架理论推广到HilbertC*-模的情形并取得了一些重要结果[7-13],这丰富了框架理论。虽然HilbertC*-模是Hilbert空间的一般化,但二者之间还是有着一些本质的差异。例如,适用于有界线性泛函的Riesz表示定理在HilbertC*-模中并不成立,这隐含着HilbertC*-模上的一些有界线性算子不可伴;HilbertC*-模中的闭子模未必正交可补等。同时需要指出,由于HilbertC*-模所嵌入的C*-代数的结构非常复杂,致使HilbertC*-模中的框架和g-框架问题处理起来要比Hilbert空间情形困难得多。此外,越来越多的研究成果表明框架理论和HilbertC*-模理论在多个方面有着紧密的联系,彼此都会因对方的发展而获益。因此,作为二者有机结合的产物,HilbertC*-模中框架和g-框架的研究工作重要且有意义。
在文献[14]中,姚喜妍讨论了HilbertC*-模中的g-框架在可伴算子作用下的一些表现。特别地,她断言:可伴算子保持HilbertC*-模中的g-框架当且仅当它是可逆的 (文献[14],定理2.4)。然而一个反例 (本文例2.2) 表明上述结论的必要条件不成立,本文的目的是修正该结论。
1 记号及引理
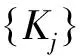
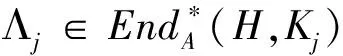
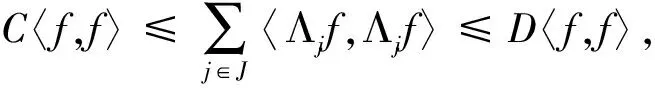
(1)
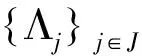
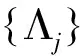
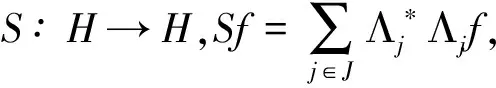
(2)
为了证明主要结论,需要如下的引理。
(1) 如果T是满射,则TT*可逆且
‖(TT*)-1‖-1·IdK≤TT*≤‖T‖2·IdK,
(2) 如果T是单射且有闭的值域,则T*T可逆且
‖(T*T)-1‖-1·IdH≤T*T≤‖T‖2·IdH,
其中IdH和IdK分别表示H和K上的恒等算子。
证明:(1) 因为T是满射,所以
N(T*)⊕R(T)=K,N(T)⊕R(T*)=H。
设f∈K使得TT*f=0,则T*f∈N(T)⊕R(T*),因此T*f=0。现在
f∈N(T*)=(R(T))⊥=K⊥={0},
即f=0,故TT*是单射。任意g∈K,存在h∈H使得g=Th。又有h1∈N(T),h2∈K使得h=h1⊕T*h2,故此g=Th=T(h1⊕T*h2)=TT*h2,这说明TT*是满射。综上可知TT*是可逆可伴算子。易见
0≤(TT*)-1≤‖(TT*)-1‖·IdK,
因此TT*≥‖(TT*)-1‖-1·IdK。又因为
〈T*f,T*f〉≤‖T‖2〈f,f〉, ∀f∈K,
所以TT*≤‖T‖2·IdK。
(2) 由 (1) 立即可得。
2 主要结果及其证明
下面的结果即为文献[14]中的定理2.4:
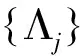
例子2.2 设l是所有有界复值序列的集合。任意j∈N∈l,定义

则A={l,‖·‖}是一C*-代数。
设H=C0表示所有收敛于零的序列的全体。任意u,v∈H,定义
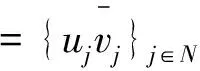
则H是A上的HilbertC*-模。
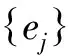
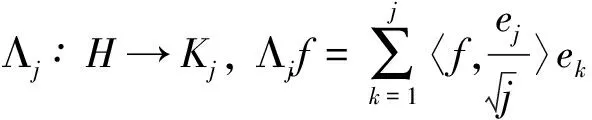
因为
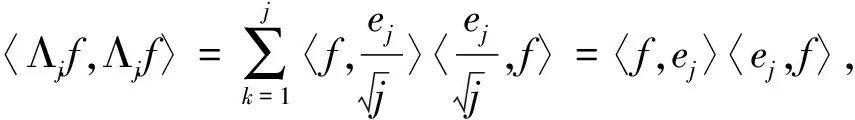
所以
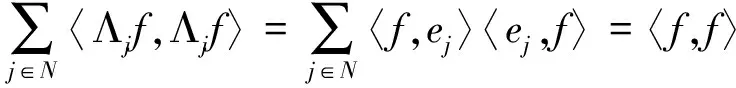
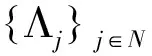
定义移位算子如下:
L∶H→H,Lej=ej+1,j∈N。
任意f,g∈H,由于
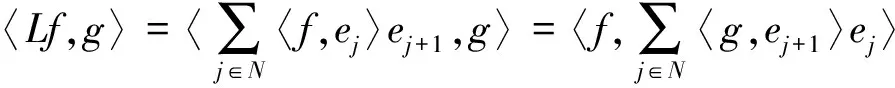
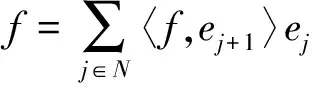
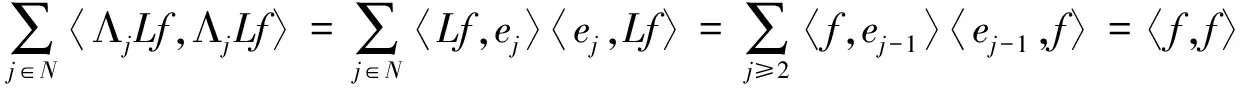
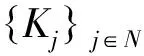
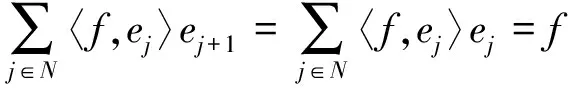
所以L*SL=IdH是可逆算子。然而,L*e1=0,故此L不可逆。
断言2.1可修正为如下形式,其证明过程无需框架算子信息。
证明:首先设L是单射且有闭的值域。任意f∈H有
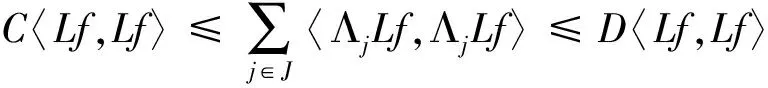
于是
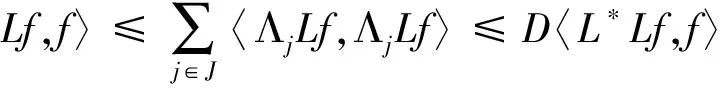
由引理1.3可知
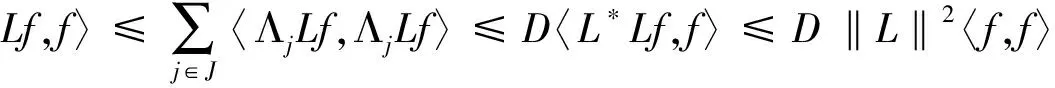
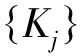
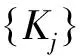
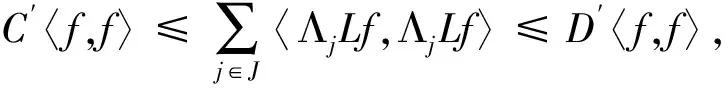
(3)
先证明L是单射。如果对某个f∈H有Lf=0,则由 (3) 式左边的不等式知C′〈f,f〉=0,所以f=0。定义算子:
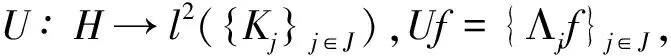
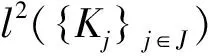
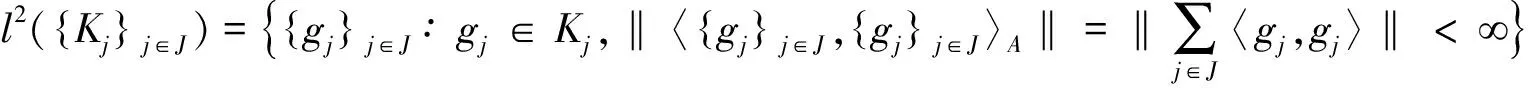
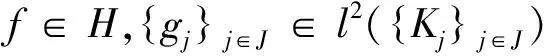
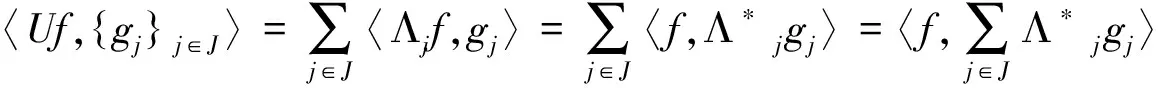
所以U是可伴的。因为任意f∈H,
C‖f‖2‖‖=‖〈Uf,Uf〉‖=‖Uf‖2,
因此U是单射且有闭的值域。设{Lfn}是R(L)中的序列使得Lfn→g,n→。由引理1.3以及 (3) 式知:
C′‖〈fn-fm,fn-fm〉‖≤‖〈U(Lfn-Lfm),U(Lfn-Lfm)〉‖≤‖U‖2‖Lfn-Lfm‖2。
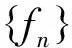
‖(U*U)-1‖-1‖Lfn-Lf‖2≤‖〈U(Lfn-Lf),U(Lfn-Lf)〉‖≤D′‖fn-f‖2。
所以由‖Lfn-Lf‖→0,n→知Lf=g,这表明R(L)是闭的。
[1] DUFFIN R J,SCHAEFFER A C.A class of nonharmonic Fourier series[J].Transactions of the American Mathematical Society,1952,72(2):341-366.
[2] DAUBECHIES I,GROSSMANN A,MEYER Y.Painless nonorthogonal expansions[J].Journal of Mathematical Physics,1986,27(5):1271-1283.
[3] BENEDETTO J J,POWELL A,YILMAZ O.Sigma-Delta quantization and finite frames[J].IEEE Transactions on Information Theory,2006,52(5):1990-2005.
[4] CANDES E J,DONOHO D L.Continuous curvet transform:II.Discretization and frames[J].Applied and Computational Harmonic Analysis,2005,19(2):198-222.
[5] SUN W C.Asymptotic properties of Gabor frame operators as sampling density tends to infinity[J].Journal of Functional Analysis,2010,258(3):913-932.
[6] SUN W C.G-frames and g-Riesz bases[J].Journal of Mathematical Analysis and Applications,2006,322(1):437-452.
[7] FRANK M,LARSON D.Frames in HilbertC*-modules andC*-algebras[J].Journal of Operator Theory,2002,48(2):273-314.
[8] KHOSRAVI A,KHOSRAVI B.Fusion frames and g-frames in HilbertC*-modules[J].International Journal of Wavelets,Multiresolution and Information Processing,2008,6(3):433-446.
[9] XIAO X C,ZENG X M.Some properties of g-frames in HilbertC*-modules[J].Journal of Mathematical Analysis and Applications,2010,363(2):399-408.
[10] ALIJANIA A.Generalized frames withC*-valued bounds and their operator duals[J].Filomat,2015,29(7):1469-1479.
[11] ASKARIZADEH A,DEHGHAN M A.G-frames as special frames[J].Turkish Journal of Mathematics,2013,37(1):60-70.
[12] XIANG Z Q,LI Y M.G-frames for operators in HilbertC*-modules[J].Turkish Journal of Mathematics,2016,40(2):453-469.
[13] XIANG Z Q.New inequalities for g-frames in HilbertC*-modules[J].Journal of Mathematical Inequalities,2016,10(3):889-897.
[14] 姚喜妍.HilbertC*-模中g-框架的一些性质[J].数学学报,2011,54(1):1-8.
A Necessary and Sufficient Condition on the Preservation of g-Frames in HilbertC*-Modules with Adjointable Operators
XIANG Zhongqi,YU Xiao,YUAN Dengbin,HUANG Feihong
(School of Mathematics and Computer Science, Shangrao Normal University, Shangrao Jiangxi 334001, China)
The present paper proves, by utilizing the method of operator theory, that an adjointable operator preserves g-frames in HilbertC*-modules if and only if it is an injective operator with closed range, which provides a correction to one existing corresponding result.
HilbertC*-module; g-frame; adjointable operator; closed range
2017-03-28
国家自然科学基金(11461055,11561057);江西省自然科学基金(20151BAB201007,20151BAB211002);江西省教育厅科技项目(GJJ151061,GJJ161051)
相中启(1979-),男,山东临沂人,讲师,博士,研究方向:分形理论与小波分析。E-mail:lxsy20110927@163.com
O177.1
A
1004-2237(2017)03-0007-04
10.3969/j.issn.1004-2237.2017.03.002

