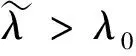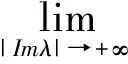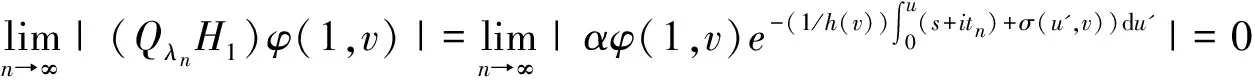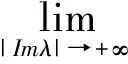具结构化的细菌种群中迁移算子的谱研究
王 胜 华
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
具结构化的细菌种群中迁移算子的谱研究
王 胜 华
(上饶师范学院 数学与计算机科学学院,江西 上饶 334001)
在Lp(1≤p<∞)空间上,研究了在一般边界条件下具结构化的细菌种群模型,讨论了这类模型相应的迁移算子的谱分析和本征值的存在性,得到了该迁移算子的谱仅由有限个具有限代数重数的离散本征值组成等结果。
结构化的细菌种群;一般边界条件;迁移算子;谱分析;离散本征值
M.Boulanouar在文献[1-2]中提出了一类具结构化的细菌种群的数学模型:
(1)
其中h(v)表示速度权重因子,ψ(u,v,t)表示由细菌成熟度u∈(0,1)和细菌成熟速度u∈(a,b)(0≤a 在生物学上,每一有丝分裂时,子细菌被看成细菌种群的一部分,它们之间存在相互关系k(u,v,v'),在数学上表示为下列一般边界条件: (2) 这里常数α,β≥0表示每一有丝分裂子细菌的平均数。 近年来,关于这类具结构化的细菌种群模型的研究较少。文献[1-2]仅在L1空间和具总转换规则(即(2)式中α=0的边界条件下进行了研究,文献[1]得到了该模型相应的迁移算子生成正不可约C0半群,文献[2]在文献[1]的基础上进一步讨论了该模型的解在一致算子拓扑意义下的渐近行为等结果。但是对这类具结构化的细菌种群模型在一般边界条件下的迁移算子的谱分析还未见研究成果,只是对速度权重因子h(v)=v的特殊情况下有些研究成果(部分可见文献[3-9])。本文在Lp(1≤p<∞)空间中对该具结构化的细菌种群模型进行研究,讨论了该模型相应的迁移算子的谱分析和本征值的存在性,得到了其迁移算子的谱仅由有限个具有限代数重数的离散本征值组成等结果。 定义索伯列夫空间为Wp: 其中h(v)为有界可测函数,且满足 假设(O1):h≥h(v)>0,a.e∈(a,b).h为常数。 定义边界算子H为: 且ψ0=ψ(0,v),ψ1=ψ(1,v)。 定义Streaming算子T和碰撞算子K及迁移算子A如下: A=T+K.D(A)=D(T). 令σ0=essinf{σ(u,v)|(u,v)∈Ω}.对λ∈C,φ∈Xp,ψ∈D(T),考虑方程 (λ-T)ψ=φ. (3) 则∀λ∶Reλ>-σ0,方程(3)式可形式地解为: (4) 取u=1,则(4)式为: (5) 根据(4)式和(5)式引入如下算子: 显然,∀λ∶Reλ>-σ0,算子Pλ,Qλ,Dλ和Eλ都是有界正算子[6],且 ‖Pλ‖≤e-(1/h)(Reλ+σ0); ‖Qλ‖≤(p(Reλ+σ0))-1/p. ‖Dλ‖≤(Reλ+σ0)-1/q; ‖Eλ‖≤(Reλ+σ0)-1. 从而(5)式和(4)式分别为: ψ1=PλHψ1+Dλφ. (6) ψ=QλHψ1+Eλφ. (7) 令 则当Reλ>λ0时,有 ‖PλH‖<1. (8) 从而算子(I-PλH)-1存在,所以 ψ1=(I-PλH)-1Dλφ. (9) ψ=QλH(I-PλH)-1Dλφ-Eλφ. (10) 即: (11) 假设(O2):碰撞算子K是有界正的,边界算子H=H1+H2,Hi≥0(i=1,2),H1是有界的;若1 定理1 若假设(O1)和(O2)被满足,且存在λ1,使得∀λ>λ1,有 rσ(PλH1)<1, (12) 则迁移算子A的谱σ(A)由至多可数个具有限代数重数的离散本征值组成。 证明:因为对λ>λ1,由(6)式知: ψ1=Fλψ1+Lλφ. (13) 若p=1,则当λ>λ2>λ1时,有(I-PλH1)-1≤(I-Pλ2H1)-1。所以 (Fλ)3=(I-PλH1)-1PλH2(Fλ)2≤(I-PλH1)-1PλH2(Fλ2)2, ∀λ>λ2. 因H2在X1上是弱紧的,则Fλ在X1上也是弱紧的,从而(Fλ)2在X1上是紧的,故由[10]之引理3.7知: ‖(Fλ)3‖≤‖(I-PλH1)-1‖‖PλH2(Fλ2)2‖→0,λ→+∞. (I-(Fλ)N)=(I-Fλ)(I+Fλ+…+(Fλ)N-1,λ∈C,λ∉S. 所以 (I-Fλ)-1=(I+Fλ+…+(Fλ)N-1(I-(Fλ)N)-1,λ∈C,λ∉S. 因此,若λ∈C,λ∉S,则(13)式变为 ψ1=(I-Fλ)-1Lλφ, (7)式变为 (λ-T)-1=QλH(I-Fλ)-1Lλ+Eλ. (14) 所以λ∈S是(λ-T)-1的极点,从而算子T的谱σ(T)由至多可数个具有限代数重数的离散本征值组成,因为A=T+K,K是有界的,所以由Kato扰动定理知:σ(A)由至多可数个具有限代数重数的离散本征值组成。 ‖PλH1‖<1. 附注2:若H满足(O2),则H2是紧的,那么存在一列有限秩算子依算子范数收敛到H2。因此,不妨设H2为秩1算子,即有 其中k1(·)∈Lp(0,1),ki(·)∈Lq[a,b],i=2,3。 定理2 条件同定理1,则 (1)Pλ,Qλ,Dλ,Eλ,Fλ和Lλ在λ∈{λ∈C|Reλ>λ1}上都是有界正算子; (2)当Reλ>λ1+ω0(ω0>0)时,(λ-T)-1和(λ-A)-1都是有界正的; (3)若σ(A)≠,则存在一个最大的实有限代数重数的离散本征值。 证明: (1)由文献[6]即知; (2)由定理1的证明过程知:∃ω1>0,使得当Reλ>λ1+ω1,有rσ(Fλ)<1。从而由(14)式知: rσ(λ-T)-1K<1。于是(λ-A)-1=(I-(λ-T)-1K)-1(λ-T)-1再由K的正性知:∀λ∶Reλ>λ1+ω0,(λ-A)-1是有界正的。 (3)由(2)和文献[12]即知(3)成立。从而本引理获证。 Γ0={λ∈C|Reλ>λ0},Γs={λ∈C|λ0 λ∈σ(A)⟺1∈σp((λ-T)-1K). 所以 σ(A)≠⟺. 又由定理2和(14)式知:∀λ∈Γ0,有 (λ-T)-1K=QλH(I-Fλ)-1LλK+EλK≥EλK. 所以 定理4 条件同定理1,则当λ∈Γ0,有 证明:由(14)式知:∀λ∈Γ0,有 ‖(λ-T)-1K‖ =‖QλH(I-Fλ)-1LλK+EλK‖ ≤‖QλH1(I-Fλ)-1LλK‖+‖QλH2(I-Fλ)-1LλK‖+‖EλK‖, 此外,对任一整数n,有 |(QλnH1)φ(1,v)|≤α|φ(1,v)|. 由控制收敛定理知: 由定理2知:Nλ=(I-Fλ)-1LλK在区域Γ0上是一致有界的,从而 此外,对任一整数n,有 由控制收敛定理知: 结合(a)(b)即得: 从而本定理获证。 定理5 条件同定理1,则σ(A)仅由有限个具有限代数重数的离散本征组成。 证明 由定理4知:Γs∩S在|Imλ|=+∞时没有聚点,且Γs∩S被限制在Γs的一个紧区域中,所以Γs∩S有限,从而σ(A)∩Γs有限,即本定理成立。 [1] BOULANOUAR M.Mathematical analysis of structured bacterial population with aggregate transition rule(Ⅰ)[J].J Comp Theo Trans,2015,44(4/5):175-197. [2] BOULANOUAR M.Mathematical analysis of structured bacterial population with aggregate transition rule(Ⅱ)[J].J Comp Theo Trans,2015,44(2):69-93. [3] BOULANOUAR M.A mathematical study for a Rotenberg mobel[J].Math Anal Appl,2002,265:371-394. [4] DEHICI A,JERIBI A,LATRACH K.Spectral analysis of a transport operator arising in growing cell populations[J].Acta Appl Math,2006,92:37-62. [5] BOULANOUAR M.Transport equation in cell population dynamics (Ⅱ)[J].Electionic Journal of Differential Equation,2010,145:1-20. [6] 王胜华,翁云芳,阳名珠.人体细胞增生中一类迁移算子的谱分析[J].数学物理学报,2010,30A(4):1055-1061. [7] LATRACHA K,MEGDICHE H.Time asymptotic behaviour for Rotenberg's model with maxwell boundary conditions [J].Discrete and continous dynamical systems.2011,29(1):305-321. [8] WU H X,WANG S H,YUAN D B.Spectral distribution of transport operator arising in cell population[J/OL].Journal of Function Spaces,Volume 2014,2014:Article ID 748792[2014-08-25].https://www.hindawi.com/journals/jfs/contents/12/. [9] 王胜华,吴红星.Rotenberg模型中一类迁移算子的谱分析[J].数学物理学报,2016,36A(6):1592-1598. [10] KATO T.Perturbation theory for Linear Operators [M].New York/Berlin Verlag:Springer,1966. [11] KAPER H G,LEKKERKERKERKER C G,HEJTMANED J.Spectral Methods in Linear Transpor Theory[M].Basrl:Birkhauder,1982. [12] VIDAV I.Existence and uniqueness of nonnegative eigenfunctions of the Boltzmann operator[J].J Math Anal Appl,1968,22:144-155. [13] DUNFORD N,SCHWARTZ J T.Linear Operators:Part I[M].New York:Interscience Publishers,1958. Spectral Research of the Transport Operator in Structured Bacterial Population WANG Shenghua (School of Mathematics & Computer Science, Shangrao Normal University,Shangrao Jiangxi 334001,China) The objective of this paper is to research the model of structured bacterial population with generalized boundary conditions inLp(1≤p<+∞) space, It is discussed the spectral analysis and the eigenvalue's existece of corresponding transport operator for this moder.So it is obtained that the spectrum of the transport operator only consisting of finitely isolate eigenvalues woth finite algebraic multiplicities. structured bacterial population; generalized boundary conditions; transport operator; spectral analysis; isolate eigenvalues 2017-04-09 国家自然科学基我们先给出一些证明过程中需要金(11461055);江西省教育厅科技项目(151051,151056) 王胜华(1956-),男,江西余干人,教授,博士,研究方向:迁移方程。E-mail:wshua@sru.jx.cn O177.2 A 1004-2237(2017)03-0001-06 10.3969/j.issn.1004-2237.2017.03.001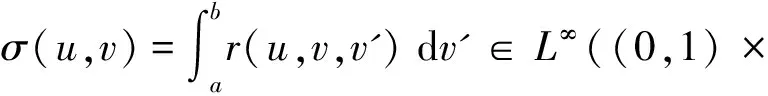
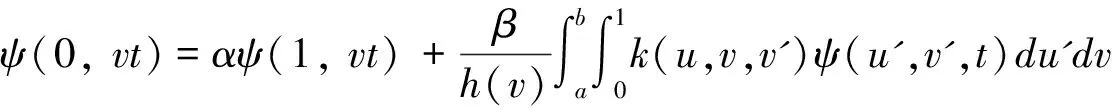
1 准备知识
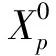
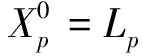
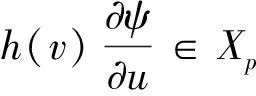
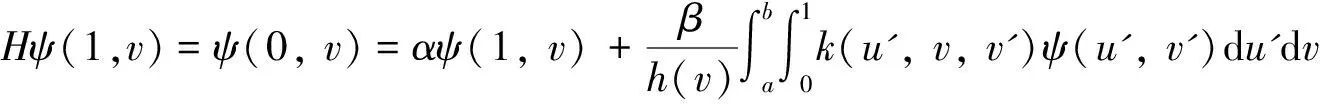
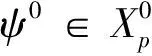

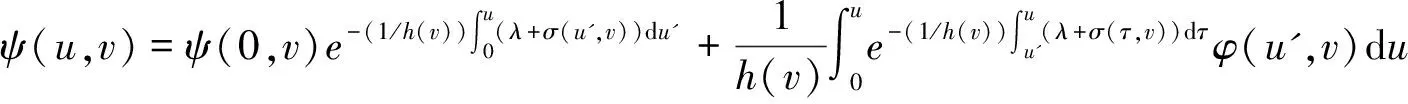
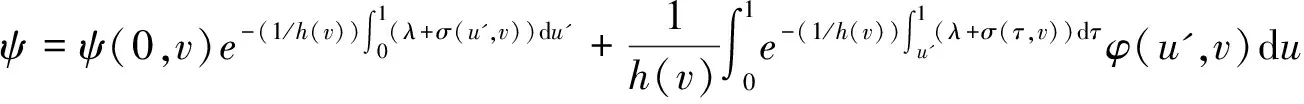
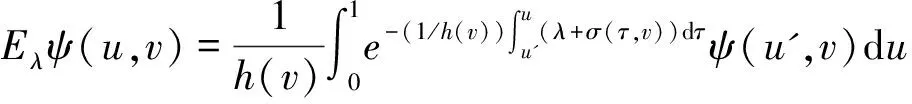

2 主要结果