插入角钢锚固件计算方法的探讨
任吉华, 贾素红
(1.潍坊五洲鼎益铁塔有限公司, 山东安丘 262100;2. 四川电力设计咨询有限责任公司, 四川成都 610000)
插入角钢锚固件计算方法的探讨
任吉华1, 贾素红2
(1.潍坊五洲鼎益铁塔有限公司, 山东安丘 262100;2. 四川电力设计咨询有限责任公司, 四川成都 610000)
文章通过对插入角钢混凝土基础抗拔试验结果的分析研究以及工程实际应用中发现的问题,指出现有DL/T 5154-2012《架空输电线路杆塔结构设计技术规定》中插入角钢锚固件的计算方法存在的问题,进而提出一种更合理的锚固计算方法。
插入角钢; 锚固件; 计算方法
插入混凝土的角钢是送电线路的重要结构构件,是铁塔和基础连接的重要方式。具有连接可靠、施工方便、耗钢量少等优点。一般由锚固件和插入角钢两部分构成。角钢斜插式基础所受的上拔或下压荷载,通过角钢与混凝土间的粘结强度及锚固件可靠地传递到混凝土基础中,但粘结强度与锚固件传递荷载和承担荷载具有不同步性,在设计中不能将两者进行简单叠加。因此其设计原则是:锚固件和插入角钢锚固不同时起作用。
杆塔上拔或下压荷载从角钢传递到混凝土基础中是一个十分复杂的过程,影响插入角钢承载力的因素很多。而我国现行的DL/T 5154-2012《架空输电线路杆塔结构设计技术规定》[1](以下简称《技术规定》)插入角钢锚固计算方法,是以“美国土木工程师协会(ASCE)结构分委会”编写的《输电铁塔设计导则》作为设计依据。在我们实际应用过程中发现当基础作用力比较大时,是由插入角钢锚固件组数控制插入角钢埋深,由锚固件计算公式得到的锚固件组数有的达到了7或8组,插入角钢埋深达到了3 m以上,约是插入角钢最小埋深的2倍多。我们经过对文献[1]插入角钢锚固件计算公式及基础抗拔试验结果的分析研究,发现其插入角钢锚固件的计算方法有值得商榷的地方。
1 《技术规定》中的锚固件计算方法
角钢锚固件承载力计算公式(其受力见图1,即文献[1]中的图9.4所示):
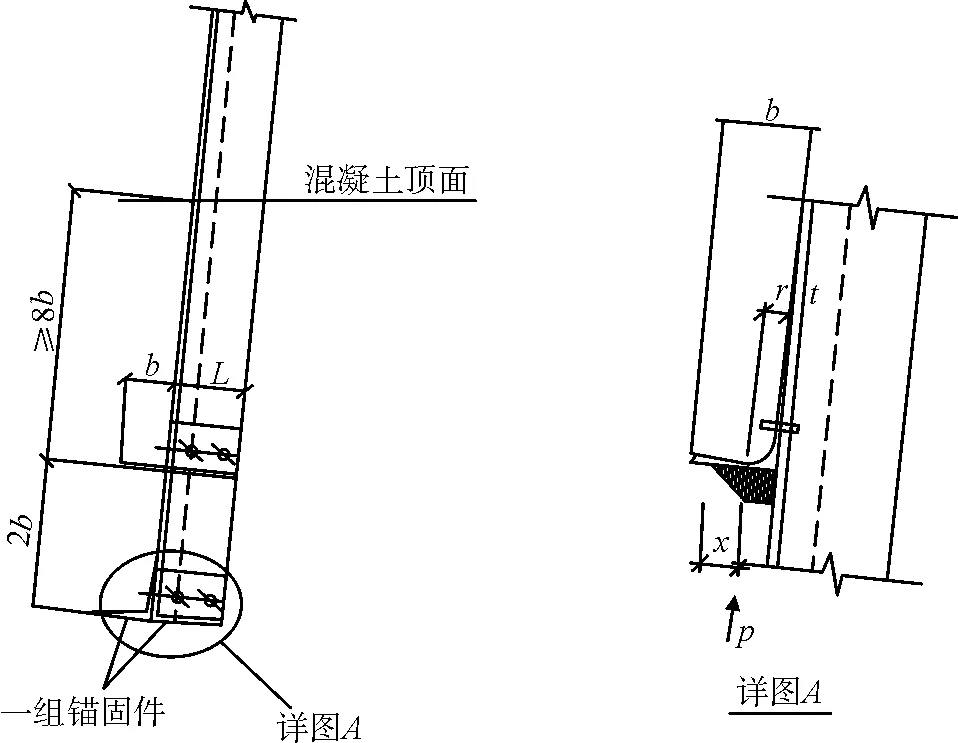
图1 插入角钢受力
(1)
P=1.19fc·L·(t+r+x/2)
(2)
n=N/P
(3)
式中:x为角钢锚固件上反力呈三角形分布长度(mm);P为单个角钢锚固件允许承受的剪力荷载(N);t为角钢厚度(mm);r为角钢内圆弧的半径(mm);fc为混凝土的抗压强度设计值(N/mm2);L为角钢锚固件的长度(mm);b为角钢锚固件的肢宽(mm),t+r+x≤b;n为角钢锚固件的数目;N为插入角钢承受的拉力或压力(N)。
2 《技术规定》锚固计算方法中存在的问题
2.1P计算公式中1.19fc取值存在问题
由公式(1)(文献[1]中的7.4.2-2式)看出,x值是以1.19fc为混凝土抗压强度设计值,角钢锚固件不屈服计算得出的。其是以角钢锚固件受压肢弧以外肢宽自由变形为依据的,但实际上其上下均有混凝土的约束作用,以此作为计算依据是否合适还值得商榷。
由上分析可知文献[1]中插入角钢锚固件的计算公式认为角钢锚固件处混凝土的强度设计值为单轴抗压强度设计值的1.19倍。
在双轴加载下的混凝土强度研究中,Kupfer等所得出的混凝土在双轴加载时的强度包络线反映了两向受压时混凝土破坏强度的基本特点[2]:当双向受压时,混凝土一向的抗压强度随另一向压应力的增加而有所加大。最大强度约在两向主应力比α=σ1/σ2=0.5处发生,约为单向抗压强度的1.22~1.27倍。当两向等压(α=1)时,强度约是单向抗压强度的1.16倍。由此可看出公式(2)中的1.19fc是按混凝土双向受压来取值的。
但是,实际上角钢锚固件上端混凝土基本上处于基础立柱断面的中间部位,受力时其受到了各个方向上的约束作用,相当于三向约束的混凝土。因此,角钢锚固件处的混凝土抗压强度为三向受压时的抗压强度,其设计值约为5fc,比1.19fc要大的多。
文献[3]中试验结果显示,在试验完成后,将混凝土块打开,检查承剪连接件或混凝土块的损坏或变形时,发现除剪坏的铆钉或其它剪力连接件外,在承剪连接件上没有发现任何的变形或变位,在承剪连接件所在的位置附近的混凝土也没有发现破裂。文献[4]中也有相似的结果,把试验后的混凝土柱子砸开,看到锚固角钢几乎被挤压成一个平面。如果将文献[4]第Ⅰ组双层角钢试验数据,用文献[1]的计算方法来反推混凝土的应力峰值,可得到4fc。这均说明了在插入角钢锚固件计算中以1.19fc作为混凝土的抗压强度设计值,来计算角钢锚固件的大小及组数是不合适的。按其设计出的插入角钢锚固件数目太多,造成混凝土和钢材的浪费,同时也增加了施工的难度。
2.2 锚固连接件的组数计算存在问题
文献[3]试验4带焊接承剪连接件的试验结果看到,插入角钢极小的力明显地由粘着摩阻传入基础。当加载到插入角钢的屈服点时,在上部的一对承剪连接件实际上承受所有的拉力90 %,同时,位于第一对承剪连接件下0.34 m的另一对承剪连接件只承受所有拉力的10 %。
文献[4]也有相似的结论:在双层锚固件中,前一个锚固件比后一个锚固件分担的荷载大4倍以上。同时从其结论中也看到,加大插入角钢埋深,可提高基础的抗拔极限承载力,但达到一定临界深度后,埋深对插入角钢承载力的增加作用不明显。
因此,如果按文献[1]中的方法来计算,锚固件的组数将偏多,从而造成插入角钢埋深过大,第一组锚固件规格偏小不安全,而其下层的锚固件富裕,有的甚至完全不起作用,造成浪费。
3 角钢锚固件计算方法探讨
从以上的分析看出,用混凝土抗压强度作为衡量锚固件承载力的计算方法是有问题的。从插入角钢锚固件被剪坏时混凝土没有破坏这一结果出发,我们可推导出一个较为合理的锚固计算方法。
3.1 角钢锚固件组数计算
从文献[3]中得知,第一组锚固件承受所有拉力的90 %,第二组承受10 %。文献[4]中,前一个锚固件比后一个锚固件分担的荷载大4倍以上。可以做出如此假定,n组锚固件受力按承受基础竖向力的等比数列分布。
假定等比系数为q,第1组承受的荷载为P1,则插入角钢极限承载力N可用下式表达:
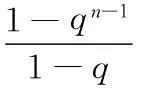
(4)
第i个锚固件承受的荷载为Pi:

(5)
如果按文献[3]所承担的比值进行计算时,q=0.1,则当n=4时,第4组承受的荷载为:
P4=0.001N
(6)
即第4组已几乎不承受荷载。
如果按文献[4]所承担的比值进行计算时,q=0.2,则当n=4时,第4组承受的荷载为:
P4=0.006N
(7)
即第4组也已几乎不承受荷载。
因此,一般插入角钢锚固件组数可取2~4组,且不宜超过4组。
3.2 角钢锚固件强度计算
从以上提到的试验数据得出,第一组锚固件的受力决定了插入角钢锚固件的大小。由角钢锚固件受力形式可知,其强度主要由剪力控制。假定第一组锚固件承受基础立柱竖向力N的0.9倍[3],则角钢锚固件强度可按以下公式进行计算。

(8)
则:
N=0.64·f·t·m·L
(9)
式中:m为第一组锚固件的个数;其它参数意义与上相同。
3.3 螺栓锚固件强度计算
而螺栓锚固件强度计算公式也可由相同原理推导如下:
(10)
则:
(11)
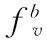
第一组锚固件距基础立柱顶面的距离及锚固件间距可按文献[3]规定取值。
3.4 与试验结果的比较
插入角钢锚固计算的原则是锚固件和插入角钢锚固不同时起作用。因此我们在比较时只能考虑锚固件所承受的荷载。
双层角钢及双层螺栓锚固件受力比较列于表1中。
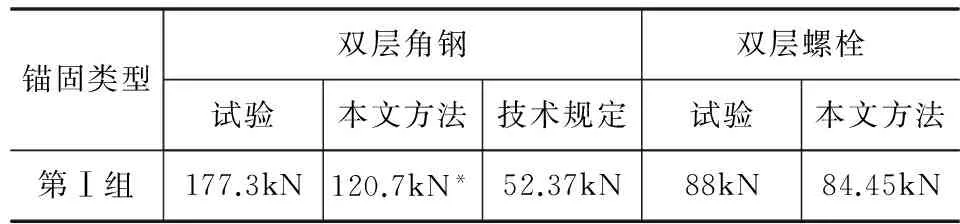
表1 锚固件受力比较
注:表中带*是按屈服强度计算得出。
以上比较中,第Ⅰ组计算参数如下:
混凝土:C25,400×400
插入角钢:Q235,∠100×8
角钢锚固件:Q235,∠100×8
螺栓:6.8级M20
由表1比较可看出,本文推导公式计算结果是比较合理的。
4 结论及建议
(1) 通过分析试验资料可以发现,试验结果均是铆钉或其它剪力连接件发生屈服,而在承剪连接件所在位置附近的混凝土没有发现破裂。说明DL/T 5154-2012《架空输电线路杆塔结构设计技术规定》中插入角钢锚固计算方法以混凝土抗压强度设计值为计算依据,是不合适的。
(2) 根据以往试验结果,本文从锚固件的极限承载力出发,推导的插入角钢锚固件公式所得到的结果与试验数据比较接近且偏于安全,具有一定的合理性。
(3) 由于插入角钢锚固件试验资料有限,此次推导的插入角钢锚固件计算公式的准确性,需要进一步的试验和实践验证。
[1] DL/T 5154-2012 架空输电线路杆塔结构设计技术规定[S].
[2] 周氏,康清梁,童保全. 现代钢筋混凝土基本理论[M]. 上海交通大学出版社,1989.
[3] E.BRANDT,E.WERSE. 插入角钢在砼基础中拉力的传递分析[J]. EPC Vol.15 No.1.
[4] 鲁先龙,程永锋. 输电线路角钢斜插式基础抗拔试验研究[J].电力建设,2004, 25(10).
任吉华(1970~),男,本科,高级工程师,从事企业经营管理工作。
TU312
A
[定稿日期]2017-03-22

