圆管变径局部水头损失的数值模拟

李 凡 齐明银 彭 玲

(1.河北建筑工程学院能源与环境工程学院，河北 张家口 075000；2.太原第一热电厂，山西 太原 030000)

圆管变径局部水头损失的数值模拟

李 凡1齐明银2彭 玲1

(1.河北建筑工程学院能源与环境工程学院，河北 张家口 075000；2.太原第一热电厂，山西 太原 030000)

管网布置及设计中，局部损失的计算非常重要，但由于其影响因素多，目前常采用经验值简化计算，误差较大.圆管变径是一种常见的管道连接方式，对其局部阻力影响因素进行研究有重要意义.通过采用数值模拟方法对供热管道设计中两次变径或跳径管段的局部水头损失进行数值模拟，绘制不同管径变化时跳径和两次变径的二维模型，分析研究了其阻力特性.模拟结果表明：相同管径和流量下，跳径的阻力损失总比两次变径的阻力损失大.

数值模拟；局部阻力；变径和跳径

0 引 言

随着城市建设飞速发展，节能、降耗及环保意识的增强，城市集中供热成为城市尤其是北方城市供热的大势所趋.通常一个城市有几个区域供热网，如何合理、经济、便捷地铺设管道，使整个集中供热系统处于一个良好的、高效的运行状态，是一个供热企业所追求的目标.供热管道设计时，按照负荷变化确定管径，合理的走向布置、管径设计及管道敷设对供热管网的正常运行意义重大.

管网布置及设计中，局部损失的计算非常重要，但由于其影响因素多，目前常采用经验值简化计算，误差较大.本文采用数值模拟的方法，模拟圆管变径和跳径在管段中水头损失的变化，分析其对资用压差的影响，寻找对供热管道阻力损失影响最小的变径方式.

1 数学模型的建立

1.1 条件假设

忽略管道壁厚的影响，以管道内径作为所研究的管段直径.且不考虑重力加速度对计算的影响.

1.2 数学模型

流体流动要遵循各种物理守恒定律，主要是质量守恒、动量守恒、能量守恒三大方程[1].在实际计算时，还要考虑不同的流态，如湍流还要遵守附加的湍流输运方程[2].

1.2.1 连续性方程

供热管网中采用水作为介质，属于不可压缩流动，且为恒定流，其连续性方程简化为:

(1-1)

式中：

ux、uy、uz分别为x、y、z三个方向上的速度分量

1.2.2 动量守恒方程

动量方程的本质就是满足牛顿第二定律.其文字描述为:对于一给定的流体微元，它的动量对时间的变化率就等于外界作用在该微元体上的各种力之和.根据这一定律，可推导出如下的x、y、z三个方向的动量方程:

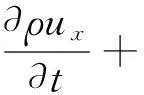
(1-2)

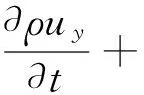
(1-3)

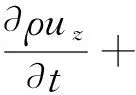
(1-4)

式中：

p—流体微元体上的压强，Pa；

τxx、τxy、τxz—为因分子粘性作用而产生的作用在微元体表面上的粘性应力τ的分量，Pa；

fx、fy、fz—分别为三个方向的单位质量力，m/s2.

1.2.3 能量守恒方程

能量守恒定律是包含有热交换的流动系统必须满足的基本定律，其本质是热力学第一定律.依据能量守恒定律，微元体中能量的增加率等于进入微元体的净热流通量加上质量力与表面力对微元体所做的功，可得其表达式为:

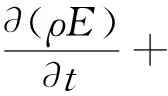
(1-5)

式中：

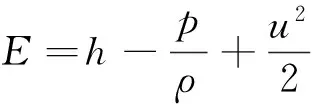
h—焓，J/kg；

hj—组分j的焓，J/kg；

keff—有效传导系数，W/(m·k)；

Jj—组分j的扩散通量；

Sh—化学反应热及体积热源项.

2 管道变径和跳径的阻力特性模拟

公称直径数值在管径序列中相邻的两管使用管件连接的方式称为变径，但对于在管径序列中公称直径数值不相邻的两管使用管件直接连接的方式称为跳径.

2.1 跳径管段模型的建立与求解

2.1.1 跳径管段模型的建立

图1 同心跳径管段网格划分

以DN125-DN80为例建立管段模型[3].直管段长度取管径的7倍，不同管径接头长度按国标选取.网格划分采用均匀与非均匀网格相结合的方法.直管道采用规则均匀的四边形网格，变径处采用包含四边形与三角形结合的非均匀网格形式.

2.1.2 跳径管段模型的求解

按照图2中的计算流程图对所设管段进行计算[4]，计算参数选择：材料(介质)为60 ℃的水，同时设置该温度下水的密度983.19 kg/m3,动力粘度为0.000469 kg/(m·s).经计算，得到压力云图和速度云图[5]，如图3、4所示.压力云图中，由红到蓝代表压力由高到低；由此可以看出进口到出口压力由高到低；在平直管道中，压力会随着沿程损失的增加而缓慢减小；在跳径处由于管径变化，使得流速发生剧烈变化，此时部分静压迅速转变为动压，使得静压值剧烈变化，因而跳径处的等压线呈现出弧形.速度云图中，同样，由红到蓝代表速度由高到低；由于进出口流量相同，故进口速度低于出口速度；在跳径处，由于管径突然变细，速度迅速增大，流体会发生扰动，在减速增压区甚至产生涡旋.

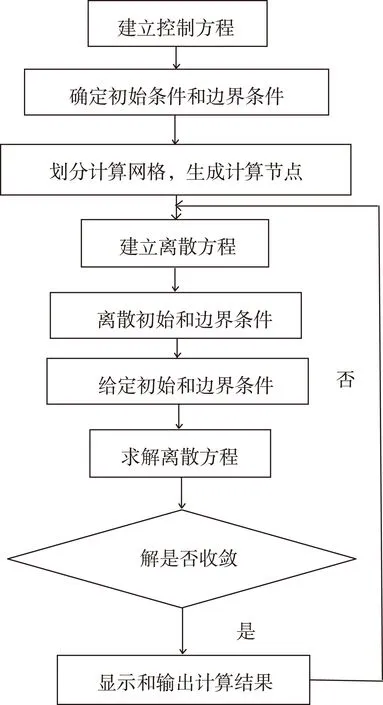
图2 计算流程图

图3 变径管段压力云图

图4 变径管段速度云图

2.2 两次变径管段模型的建立与求解

2.2.1 两次变径管段模型的建立

以DN125-DN100-DN80的管段为例，直管段长度取管径的7倍，不同管径接头长度按国标选取.管径最小的管段取比摩阻70 Pa/m，依此计算管道入口流速、湍动能及湍流耗散率.采取与变径同样的方法建立求解模型，以DN125-DN100-DN80的管段为例分析其阻力损失的变化.划分的网格如图5所示.

图5 DN125-DN100-DN80管段模型

2.2.2 两次变径管段模型的求解

按图2的流程进行计算，材料的选取与跳径的选择相同.查看压力云图、速度云图如图6、7所示.由图6、7可以看出压力云图中，由红到蓝代表压力由高到低；由此可以看出进口到出口压力由高到低；在平直管段，静压值会随沿程阻力损失的增大而渐渐变小，在变径处由于管径变细使得流速增大静压迅速向动压转化，因而此处静压值变化较大，图形呈现弧形，这是由于接头处扰动涡旋的产生.速度云图中，同样，由红到蓝代表速度由高到低；由于进出口流量相同，故进口速度低于出口速度；在变径处，由于管径突然变细，流速增大，流动会发生扰动，在减速增压区甚至产生涡旋，此时速度变化曲线也呈弧形.

图6 DN125-DN100-DN80管段压力云图

图7 DN125-DN100-DN80管段速度云图

2.3 两次变径与跳径的阻力比较

将上述模拟结果得到的数据分析比较如下表1所示.

表1 变径与跳径模拟结果

表1可以明显看出变径比跳径的压力损失更大，为验证模拟结果的可靠性，选择多个管段进行模拟，对于不同管径(DN40-DN300之间)同心接头下，变径与跳径进出口压力及ΔP如下表2所示：

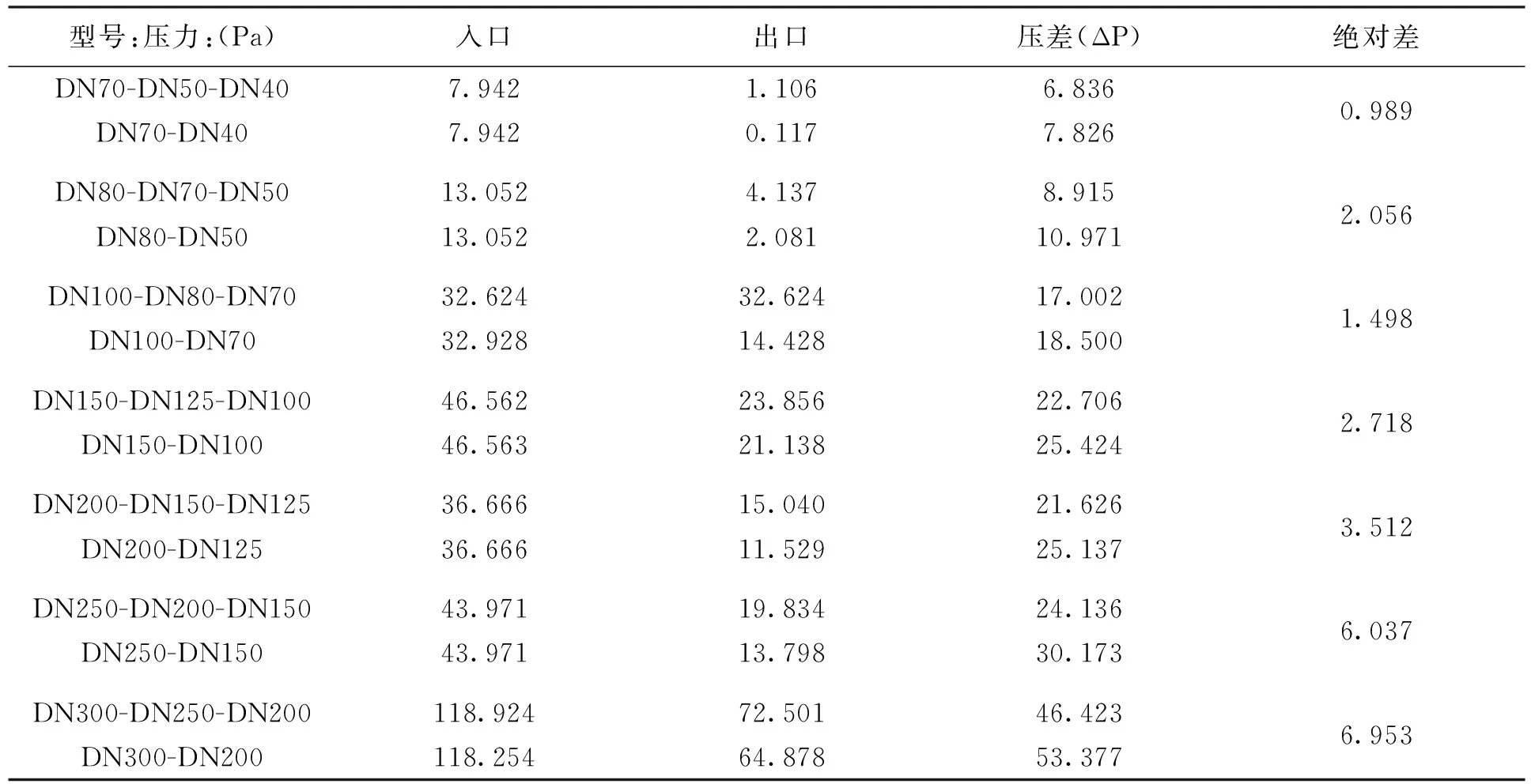
表2 不同管径下跳径与变径的模拟结果

从表2中数据可以看出：阻力损失在单位(Pa)这个数量级的前提下，相比较而言，对于相同管径(DN40-DN300之间)同心变径下进出口的阻力损失总比跳径的小.从能量守恒的角度分析，两次变径时管径变化较小，导致流速的变化较小，但是跳径时管径变化较大，导致流速的变化也较大；同时两次变径会产生两次微弱的扰动，而跳径在变径位置会产生剧烈的扰动，较二次扰动强烈的多，因此，在扰动过程中两次变径所产生粘性耗散和壁面摩擦热损失会比跳径的损失较小；虽然两次变径与跳径都存在沿程损失，但是局部阻力损失仍占主导地位；所以两次变径管段比跳径管段的阻力损失更小一些.

除此之外，阻力损失在单位(Pa)这个数量级的前提下，总体来说，它们阻力损失的差值对于管网中的资用压差的影响都很小.但是管径越大两次变径与跳径阻力损失之间的绝对差值越大，而DN100-DN80-DN70和DN100-DN70之间的阻力损失产生的绝对差值比相邻管道都小.对于小于DN150的管道采用两次变径和跳径时的阻力损失产生的绝对压差随管径的增大变大的幅度较小；而对于大于DN150的管道采用两次变径和跳径时的阻力损失产生的绝对压差随管径的增大变大的幅度较大.因而，在经济条件合适又便于施工的情况下，小于DN150的管径既可以采用两次变径也可以采用跳径.而大于DN150的管径更适合于用两次变径.

3 结 论

通过对不同管径的管段模拟[6]可以得出：对于相同管径(DN40-DN300之间)同心变径下，两次变径流体进出口阻力损失总比跳径的阻力损失小.从能量守恒的角度分析，这是因为，两次变径会会产生两次微弱的扰动，在扰动过程中粘性耗散和壁面摩擦热损失会比跳径的损失较少；而跳径会在变径位置产生剧烈的扰动，在扰动过程中粘性耗散和壁面摩擦热损失会比跳径的损失很大.虽然两次变径会与跳径都存在沿程损失；但是在整个过程中，局部阻力损失占主导地位；所以两次变径管段比跳径管段的阻力损失更大一些.除此之外，从压力云图中可以看出压力在接头前后处会发生的变化很明显，而在平直管段中压力变化较弱；从速度云图中可以看出速度在接头前后处的速度变化比较明显，而在平直管段中速度几乎不变；由此也可以看出，流体在变径位置处的损失较平直管段损失占主导位置.所以为减小资用压差，尽量采用两次变径管道.

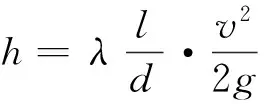
[1]王福军.计算流体动力学分析——CFD软件原理与应用.北京：清华大学出版社，2004

[2]吴持恭.水力学：上册[M].北京：高等教育出版社，2007.129～155

[3]李卓，俞坚，马重芳.小通道单相流体突扩和突缩局部阻力特性[J].化工学报，2007，58(5)：1127～1131

[4]Frank.M.White.Fluid Mechanics[M].北京：清华大学出版社，2004.386～391

[5]陈新进，王庆顺，孙伟.基于Fluent的蓄热体传热过程的数值模拟.机械工程师.4：71～73.2015

[6]赵宝峰，金英子，卢玉邦，等.对突然扩大局部水头损失的初探[J].东北农业大学学报,1997，28(2)：175～178

Numerical Simulation on Local Resistance of Reducing Pipe

LIFan1,QIMing-yin2,PENGLing1

(1.Hebei University of Actecture,Zhangjiakou,Hebei 075024;2.Taiyuan First Thermal Power Plant of,Taiyuan,Shanxi 030000)

The calculation for partial loss is very important in the layout and design of a pipe system.However,because there are many factors which could affect the results,the empirical coefficient method is applied to the calculation which is inaccurate.Reducing Pipe is a common pipe connection way,which is significant to analyze the factors influencing local resistance.Through the numerical simulation method,the numerical simulation of the local head loss of the two variable or jump pipe sections in the design of the heating pipe is carried out,the two-dimensional model of jump diameter and two variable diameters under different diameters is drawn,and the resistance characteristic is analyzed.The simulation results show that the resistance loss of the jump diameter is larger than that of the two diameters.

numerical simulation;local resistance;variable diameter or jump diameter

2016-12-05

李凡(1994-)女，研究生在读，主要研究方向：供热系统的动态仿真.

10.3969/j.issn.1008-4185.2017.01.023

TU 82

A