柔性串联机械臂的模糊自适应滑模控制系统设计

王爱国， 王其东

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽机电职业技术学院 汽车工程系,安徽 芜湖 241002)

柔性串联机械臂的模糊自适应滑模控制系统设计

王爱国1,2， 王其东1

(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.安徽机电职业技术学院 汽车工程系,安徽 芜湖 241002)

针对柔性串联机械臂传统控制方式的轨迹跟踪精度存在误差较大的缺陷,文章提出了一种结合柔性串联机械臂弹性动力学方程和模糊自适应滑模控制(sliding mode control,SMC)的控制方法。采用运动弹性动力学(kineto-elastic-dynamics,KED)法,结合系统的约束方程,建立了机械臂的弹性动力学方程,为系统提供控制对象模型;将模糊自适应算法与SMC控制器相结合,设计出一种新型SMC控制器,并运用Lyapunov函数验证该新型SMC控制器的稳定性;基于S-Function函数,建立机械臂的Matlab/Simulink仿真框图,对机械臂进行仿真分析。结果表明,模糊自适应SMC控制器具有轨迹跟踪精度高和稳态误差小的特点,验证了新型SMC控制器的有效性。

柔性串联机械臂;弹性动力学方程;模糊自适应;滑模控制(SMC);Simulink仿真

机械臂是一种能实现自动定位控制且具有丰富编程方式的多功能机构,作为“中国制造2025”战略的重要研究领域,其在工业自动化生产加工过程中有着重要的地位[1]。柔性串联机械臂是一个具有非线性、时变性和强耦合特征的复杂多输入多输出(multiple-input multiple-output,MIMO)系统,传统的控制策略由于稳定性差、抗干扰能力弱等因素,使得系统难以达到有效的控制效果[2]。因此,运用新的智能控制策略来提高柔性串联机械臂的控制精度,逐渐成为学者们关注的焦点。

滑模控制(sliding mode control,SMC)即滑模变结构控制，响应速度快,无需系统在线辩识、简单易实现,且具有对外界参数摄动及扰动鲁棒性强的优点,在柔性串联机械臂的控制系统中已得到广泛运用[3];文献[4]以刚性机械臂为研究对象,采用新型滑模面和模糊幂次趋近律相结合的方法,设计了一种新型SMC控制器,提高了系统的趋近运动速度,但所建立的机械动力学方程不能很好地反映机械臂的实际情况;文献[5]采用绝对坐标法,建立了空间柔性机械臂的动力学模型,并研究了机械臂的控制策略和轨迹优化设计,机械臂的残余振动得到了有效抑制,但动力学建模的步骤和参数整定较复杂;文献[6]基于柔性关节机器人,设计了一种前馈补偿和模糊滑模相结合的控制器,并对其进行了实验分析,但没有讨论控制器在非线性因素下的稳定性问题;文献[7]针对液压驱动单元的三自由度柔性机器人,提出了一种基于指数趋近律的SMC控制算法与模糊控制算法相结合的控制方式,但控制信号与机构自由度维数的关联性不强。

为改善并提高柔性串联机械臂的轨迹跟踪精度,本文将模糊自适应算法和SMC控制器相结合,设计了一种以二自由度的柔性串联机械臂为研究对象的控制系统,建立了机械臂的弹性动力学方程和Simulink仿真框图,并研究了机械臂在新型控制器下的轨迹跟踪误差曲线。

1 建立柔性机械臂的弹性动力学方程

对于n自由度的柔性串联机械臂而言,考虑到机械臂的刚-柔耦合特性、铰链间的摩擦、柔性杆件的变形及外界干扰等因素的影响,其弹性动力学方程由有限单元的装配方程和系统的约束方程2个部分组成[8]。

在柔性串联机械臂的弹性动力学方程建模过程中,将刚度小且弹性变形大的杆件等效为弹性单元,刚度大且弹性变形小的构件等效为刚性单元,并基于运动弹性动力学(kineto-elastic-dynamics,KED)法来建立柔性串联机械臂的弹性动力学方程。

将二自由度的柔性串联机械臂作为研究对象,其结构简图如图1所示。建立如图1所示的坐标系A-xy,点O为末端执行器的中点；柔性杆AB的长度为l1,质量为m1,与x轴正向的夹角为θ1;柔性杆BC的长度为l2,质量为m2,与杆AB正向的夹角为θ2。

图1 二自由度柔性串联机械臂结构简图

1.1 系统的弹性动力学方程

串联机械臂的柔性杆件以梁单元为研究对象,在浮点坐标系下,运用有限元法,可得到梁单元的弹性动力学方程[9]为:

(1)

根据有限元的叠加原理,结合转换矩阵R,将局部坐标系下的梁单元弹性动力学方程装配成系统的弹性动力学方程,则

(2)

其中,U为全局广义坐标向量。

为了减少广义坐标的数量,采用左乘R的转置矩阵RT的方法,代入(1)式可得系统的弹性动力学方程为:

(3)

其中,M为等效质量矩阵;C为等效阻尼矩阵;D为等效刚度矩阵;P为等效广义外力矩阵。

1.2 系统的约束方程

为了更好地建立柔性串联机械臂的弹性动力学方程,尽可能地减少铰链耦合、摩擦和弹性变形对建模的影响,在得到系统弹性动力学方程的基础上,还需要得到刚体约束、弹性约束和动力学约束3个约束方程[10]。

对于刚体约束方程,由机械臂的几何关系(见图1)可得：

(4)

将各矢量投影到坐标系A-xy的坐标轴,有

(5)

其中,(xA,yA)为点A的坐标；(xC,yC)为点C的坐标。

对于弹性约束方程,建立的坐标系如图2所示。图2中,虚线为机械臂的实际位移状况;A-xy为全局坐标系;O′-x′y′为运动后的局部坐标系。

图2 实际位移图

因此,坐标系O′-x′y′到坐标系A-xy的变换矩阵为:

(6)

点O和点O′在坐标系A-xy的坐标向量满足如下关系:

(7)

其中,(xO′,yO′)为点O′的坐标,xO′=xO+ΔxO,yO′=yO+ΔyO。点C和点C′在坐标系A-xy中的坐标向量满足如下关系:

(8)

其中,(xC,yC)为点C的坐标；(xC′,yC′)为点C′的坐标；xC′=xC+ΔxC,yC′=yC+ΔyC′。假设末端执行器在运动过程中不发生形变,则执行器中点到支链端点的长度没有改变,有

(9)

(9)式化简可得:

(10)

综上所述,(6)～(10)式为机械臂的弹性约束方程。

对于动力学约束方程,可通过求解刚性串联机械臂的动力学方程来描述,而求解刚性串联机械臂的动力学方程一般采用拉格朗日法进行求解,其通用表达式[11]如下:

(11)

各矩阵的具体参数如下:

2 控制器的设计

2.1 传统的SMC控制器

SMC从本质上看是一种特殊的非线性控制策略,在系统的动态运动过程中,不断地调整系统的运动状态,迫使系统按照预定的滑模状态轨迹进行运动。设计SMC控制器首先需要选择一个稳定和理想的切换函数s(x),然后确定一个控制律u(x)迫使系统在一定特性下沿规定的轨迹运动,最后运用Lyapunov函数证明SMC控制器的稳定性。

传统的切换函数定义如下:

(12)

其中,e为系统误差;C=diag(C1,…,Cn),Ci>0。

常用的一种滑模趋近律是幂次趋近律,其表达式为:

(13)

其中,k>0;0<α<1。

当系统的运动状态靠近滑模面时,趋近速度较大,可通过减小α值来降低趋近速度,削弱抖振;当系统的运动状态远离滑模面时,趋近速度较小,可通过增大α值来提高趋近速度,以缩短趋近时间。

2.2 模糊自适应SMC控制器

对于传统的SMC控制器,切换函数中的参数C和幂次趋近律中的参数α通常都为特定的常值矩阵和常数。因此,对于柔性串联机械臂这种复杂的非线性系统,往往不能达到预期理想的控制效果。模糊自适应SMC控制器通过模糊自适应算法,对SMC控制器的参数C和参数α进行在线实时修正,以提高系统的轨迹跟踪精度。

模糊自适应SMC控制器的示意图如图3所示。

图3 模糊自适应SMC控制器示意图

(14)

高斯型隶属函数示意图如图4所示。

图4 高斯型隶属函数示意图

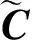
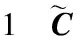
表的控制规律

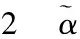
表的控制规律

2.3 控制器的稳定性分析

(15)

(16)

则

(17)

(18)

其中,KD=diag(Ki),Ki>0；W=diag(ωf1,…,ωfn),|ωfi|≥|ωi|。将(18)式代入(15)式得:

(19)

因此,系统满足滑动模态的存在条件和到达条件,新型SMC控制器是稳定的。

3 仿真分析

为减少建模误差对控制精度的影响,采用Matlab/Simulink建立机械臂的控制系统框图,运用S-Function函数编写机械臂的动力学方程和模糊自适应滑模控制律,如图5所示。其中,Sine Wave为期望的运动轨迹,S-Function为系统的控制律;S-Function1为机械臂的动力学方程,Clock为计时器。系统运行的所有数据全部导入工作空间(To Workspace),运用绘图程序得到机械臂的轨迹跟踪图形。

图5 机械臂控制系统框图

机械臂的位移追踪误差和速度追踪误差曲线如图6所示。

由图6可知,机械臂在2 s左右出现了一定的抖振现象,这是由于运动点正处于趋近阶段造成的。因模糊自适应SMC控制器具有很强的抗干扰能力,随后机械臂的位移和速度误差值处于0点附近,实际运动轨迹与期望运动轨迹的重合度较高。

经模糊自适应SMC控制器处理后的系统输入曲线如图7所示,对机械臂的输出力进行补偿的曲线如图8所示。

图6 机械臂位移追踪误差和速度追踪误差曲线

图7 控制输入曲线

图8 补偿曲线

4 结 论

本文采用KED法建立了柔性机械臂的弹性动力学方程,为系统的控制仿真提供了控制对象。基于模糊自适应SMC控制器和S-Function函数,建立了机械臂的Matlab/Simulink仿真框图。在此基础上,对该新型SMC控制器进行了仿真分析,结果表明,模糊自适应SMC控制器可以使机械臂获得较高的轨迹跟踪精度和较小的稳态误差。

[1] 张萍萍.基于PLC的气动机械手控制系统设计[D].成都:电子科技大学,2013.

[2] WANG L,SHENG Y,LIU X.A novel adaptive high-order sliding mode control based on integral sliding mode[J].International Journal of Control,Automation and Systems,2014,12(3):459-472.

[3] 王爱国,陈健伟.基于MATLAB的3-RPS并联机构控制系统仿真[J].工程设计学报,2016,23(2):172-180.

[4] 杨永泰.空间柔性机械臂动力学建模、轨迹规划与振动抑制研究[D].北京:北京理工大学,2014.

[5] MOBAYEN S.An adaptive fast terminal sliding mode control combined with global sliding mode scheme for tracking control of uncertain nonlinear third-order systems[J].Nonlinear Dynamics,2015,82(1):1-12.

[6] AMER A F,SALLAM E A,LAWADY W M.A new adaptive fuzzy sliding mode control using fuzzy self-tuning for 3 DOF planar robot manipulators[J].Applied Intelligence,2014,37(4):1-7.

[7] 陈泽塔.柔性机械臂的建模与控制研究[D].西安:西安电子科技大学,2012.

[8] ABE A.Trajectory planning for residual vibration suppression of a two-link rigid-flexible manipulator considering large deformation[J].Mechanism and Machine Theory,2012,44(9):1627-1639.

[9] FARIS W F,ATA A A,SA ADEH M Y.Energy minimization approach for a two-link flexible manipulator[J].Journal of Vibration and Control,2013,15(4):497-526.

[10] 崔亮.机器人柔顺控制算法研究[D].哈尔滨:哈尔滨工程大学,2013.

[11] MOBAYEN S.An adaptive chattering-free PID sliding mode control based on dynamic sliding manifolds for a class of uncertain nonlinear systems[J].Nonlinear Dynamics,2015,82(1):1-8.

[12] SHENG Y Z,GENG J,LIU X D,et al.Nonsingular finite-time second order sliding mode attitude control for reentry vehicle[J].International Journal of Control,Automation and Systems,2015,13(4):853-866.

(责任编辑 胡亚敏)

Design of fuzzy-adaptive sliding mode control system for flexible series manipulator

WANG Aiguo1,2, WANG Qidong1

(1.School of Automobile and Traffic Engineering, Hefei University of Technology, Hefei 230009, China; 2.Dept. of Automotive Engineering， Anhui Technical College of Mechanical and Electrical Engineering, Wuhu 241002, China)

The conventional controller for flexible series manipulator has a defect that the trajectory tracking error is large. In this paper, a control system based on the elastic dynamic equation and the fuzzy-adaptive sliding mode control(SMC) was designed. Firstly, by using the kineto-elastic-dynamics(KED) method, the elastic dynamic equation of manipulator was established with the constraint equation of system, which was provided for the control system. Secondly, a new sliding mode controller was presented by combining the fuzzy-adaptive algorithm with the sliding mode controller, and the stability of the new sliding mode controller was verified by using the Lyapunov function. Finally, the Matlab/Simulink simulation diagram of manipulator was established based on the S-Function, and the simulation analysis was carried out. The results show that the fuzzy-adaptive sliding mode controller has high precision and small steady-state error, which verifies the effectiveness of the new sliding mode controller.

flexible series manipulator; elastic dynamic equation; fuzzy-adaptive; sliding mode control(SMC); Simulink simulation

2016-12-08；

2017-02-24

安徽省高等学校自然科学基金重点资助项目(KJ2016A138;KJ2017A753);安徽省高校优秀青年人才支持计划资助项目(皖教秘人(2014)181号文件)

王爱国(1976-),男,安徽合肥人,合肥工业大学博士生,安徽机电职业技术学院副教授； 王其东(1964-)，男，安徽阜南人，博士，合肥工业大学教授，博士生导师.

10.3969/j.issn.1003-5060.2017.05.005

TH112

A

1003-5060(2017)05-0601-06