基于流形学习的多光谱优化波段选择算法研究

顾章源,刘 翔,苏 枫,郑翰清,刘 达,李建勋

(1.上海交通大学 电子信息与电气工程学院,上海 200240; 2.上海航天控制技术研究所,上海 201109; 3.中国航天科技集团公司 红外探测技术研发中心,上海，201109)



基于流形学习的多光谱优化波段选择算法研究

顾章源1,刘 翔2，3,苏 枫2,郑翰清2,刘 达1,李建勋1

(1.上海交通大学 电子信息与电气工程学院,上海 200240; 2.上海航天控制技术研究所,上海 201109; 3.中国航天科技集团公司 红外探测技术研发中心,上海，201109)

为从多光谱图像特征提取的角度进行优化波段选择，在充分描述数据结构特征的同时使提取选择的特征有明确的物理意义，对基于流形学习算法的优化波段选择算法进行了研究。用判别局部排列(DLA)算法对多光谱数据进行预处理，选取正负样本，利用样本信息，以目标分类为目的进行特征提取。利用特征提取的结果，从特征提取的角度分析当前各谱段对所提取的主特征贡献的总信息量和贡献率，给出了基于权值和基于贡献率的两种优化波段选择算法，分别基于权值和贡献率进行特征选择。用正负样本的可分性可快速高效降维，同时又能保留多光谱图像原物理特性。实测数据验证了优化降维后的5个谱段能保留原数据的物理特性，目标识别概率提高约2%，计算复杂度降低约50%。优化选择的谱段有助于新一代多光谱探测器的研制和应用。

多光谱； 波段选择； 降维； 流形学习； DLA算法； 特征； 权值； 贡献率

0 引言

多光谱成像技术不同于传统的单一宽波段成像技术，它将成像技术与光谱测量技术结合，获取的信息不仅包括二维空间信息，而且包含随波长分布的光谱辐射信息，形成所谓的“数据立方”。丰富的目标光谱信息结合目标空间影响极大提高了目标探测的准确性，扩展了传统探测技术的功能。但波段数量较多、波段间相关性较大同时也带来信息冗余，数据存储、处理难度增大，算法设计复杂，实时性变差等问题，因此对多光谱数据进行优化波段选择显得尤为重要[1]。优化波段选择实质是一个降维过程，目的是在最大程度保留重要信息的前提下剔除冗余信息及噪声信息。文献[2]利用数个波段协方差矩阵的特征值选取信息量丰富的任意波段组合；文献[3]提出最佳指数准则(OIF)，综合了波段组合的信息量及其相互间的相关系数，可同时选取信息量大且彼此关系性弱的波段组合；文献[4]提出了一种渐进的基于波段优先级排序的波段维数处理方法。

现有的降维算法主要分为基于变换的特征提取和基于非变换的特征选择两类[5]。特征提取利用原始数据的全部波段信息，通过若干变换以产生较少的新特征，原始数据可被新空间的低维数据代替，从而实现降维。常见的特征提取算法有主成分分析法(PCA)、离散小波变换法、正交子空间投影法等[6]。特征提取的优点是快速高效，且效果一般好于特征选择，缺点是改变了多光谱图像原有的物理特性。特征选择主要从全部波段中选出有代表性的波段子集组成最优波段，在保留重要信息情况下最优波段的信息能代表其他波段的信息，从而实现降维。常见的特征选择算法有熵与联合熵法、最佳指数法、波段指数法等[7]。特征选择可保留多光谱图像原有的物理特性。

特征提取和特征选择算法同样作为降维算法用于模式识别和数据处理等领域，从高维数据中提取或选择特征对数据进行描述分析。但就两类算法的流程而言，特征选择算法应用于从当前数据中，选择有限个有明确物理意义的数据作为当前数据的有效描述，保持了数据的明确物理意义；特征提取算法应用的相对特征选择更广泛，可从最优描述，最优分类的角度，在高维数据中提取新特征，新特征是原特征的一个映射，其在对数据描述和识别等方面较特征选择更具优势，但往往失去了明确的物理意义。为此，提出了其他的波段选择算法。基于权值和基于贡献率两种优化波段选择算法分别依据权值和贡献率的概念，对当前各谱段所提取特征的重要程度进行分析。显然，谱段在提取的特征中所占比重越大，说明其包含对当前图像分类识别有效的信息更多。因此，基于权值的优化波段选择算法期望从特征贡献权值的角度进行波段选择。

流形学习是近来较热门的一个研究领域，流形是线性子空间的一种非线性推广，所谓流形(manifold)就是一般的几何对象的总称。流形学习的目的是寻找嵌入在高维观测空间的低维流形，即通常意义下的特征[8]。本文基于流形学习DLA算法，利用其对多光谱数据进行预处理，提出了基于权值和基于贡献率的两种优化波段选择算法，根据正负样本快速高效选取优化波段，并保留原数据的物理特性。优化选择的谱段有助于新一代多光谱探测器的研制和应用。

1 问题描述

1.1 多光谱

由于任何具有一定温度的物体内部带电粒子都在不停运动，因此它们都会向外界不断地进行电磁辐射。电磁辐射波谱如图1所示，它涵盖了红外、可见光和紫外波段。红外辐射又被称为红外线，常用的探测波段是3～5 μm的中红外波段和8～14 μm的中远红外波段。

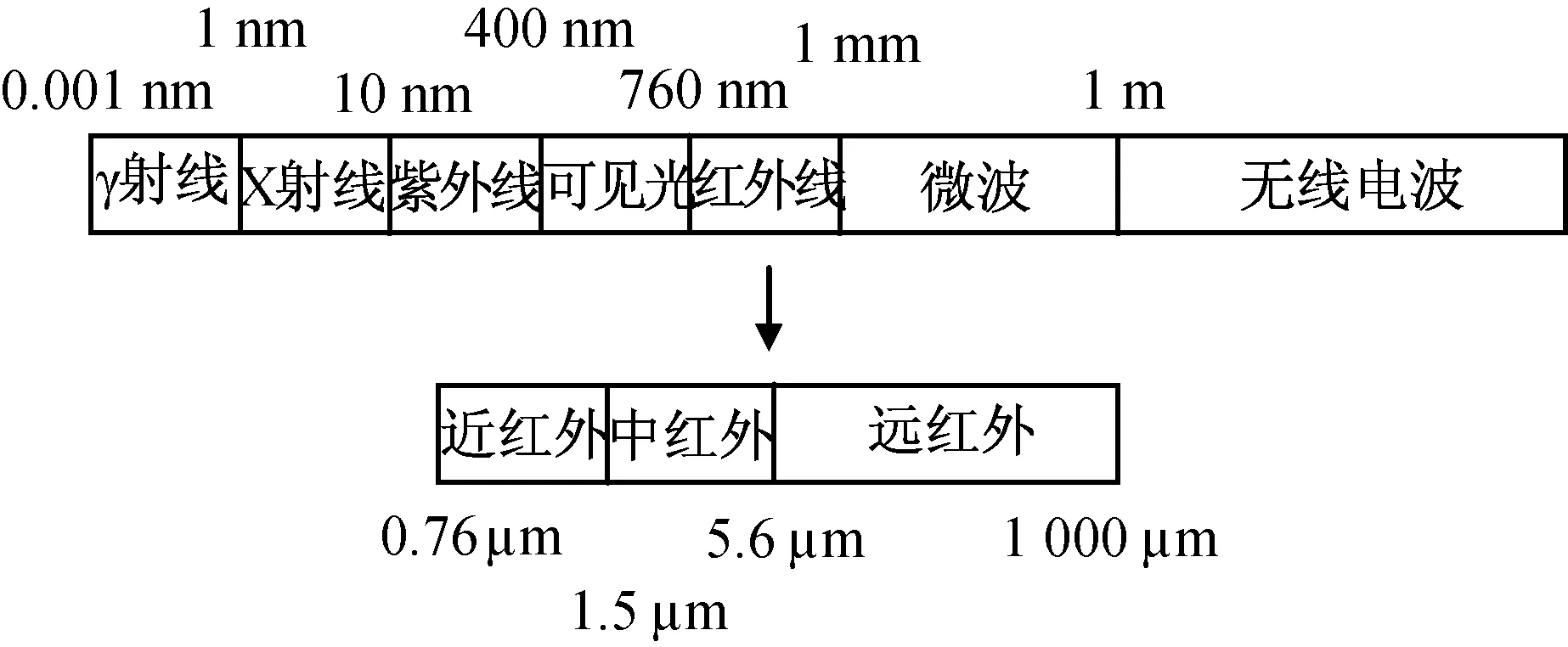
图1 电磁光谱及红外辐射Fig.1 Infrared radiation and electromagnetic spectrum

光谱图像中同时包含二维空间信息和光谱信息，构成“数据立方”(如图2所示)。目标光谱信息与空间信息的结合能提供新的特征信息，与传统探测技术相比，探测性能明显增强。目前，多光谱成像技术被广泛用于遥感和探测等领域。

图2 数据立方Fig.2 Data cube

1.2 DLA算法

文献[9-10]提出了一种判别局部排列的降维算法(DLA)，这是一种基于目标驱动的流形学习算法。与PCA算法不同，目标驱动的流形学习算法利用正负样本信息，PCA算法保持采样数据方差的最佳投影子空间，而基于目标驱动的流形学习算法以目标分类为目的提取特征。DLA算法形成的框架可统一现有的基于谱分析的各种经典降维算法，其中包括PCA算法。

对给定的样本点xi，可根据类别信息将其他的点分成两种：xi的同类点和xi的异类点。在xi的同类点中选择最近邻的k1个点，称之为同类近邻点，记为xi1，…，xik1；在xi的异类点中选择最近邻的k2个点，称之为异类近邻点，记为xi1，…，xik2。将xi1，…，xik1与xi1，…，xik2组合，可得一个对应xi的局部排列

令相应的低维输出为

判别局部排列的方法是：在低维空间中，期望给定点与其同类近邻点间的距离尽可能小，与其异类近邻点间的距离尽可能大，如图3所示。图3中：左半部分为原始数据空间中第i个局部排列，由xi、同类近邻点(xi1，xi2，xi3)、异类近邻点(xi1，xi2)组成；右半部分为在低维空间中在局部排列上期望得到的结果：低维坐标yi1，yi2，yi3与yi尽可能靠近，而yi1，yi2尽可能远离yi。

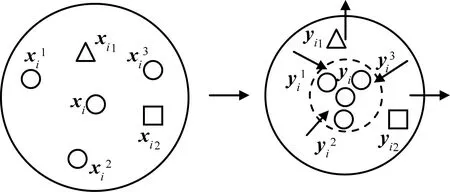
图3 判别局部排列Fig.3 Determining local alignment

对低维空间的局部排列，期望给定的点与其同类近邻点间的距离尽可能小，与其异类近邻点间的距离尽可能大，则有

(1)

(2)

用一个线性操作表示该局部排列上的判别，有

(3)

式中：β为在[0，1]范围内缩放因子，用于对不同的类内聚类和类间距离进行统一。

定义系数向量

将ωi代入式(3)，可简化为

(4)

式中：Yi为局部排列Xi相应的低维输出；Fi为局部排列上样本点的索引集合；Ik1+k2为(k1+k2)×(k1+k2)维单位阵；ek1+k2=[1 … 1]T∈Rk1+k2。此处：

定义

(5)

根据所得的部分优化Li，将其全部叠加，得整体排列上的判别

(6)

(7)

2 考虑多光谱特性的检测和跟踪算法研究

判别局部排列降维属于特征提取范畴，能快速高效地降维，但它改变了多光谱图像原有的物理特性，导致对降维后图像的解释变得困难。判别局部排列降维主要包括两个步骤：首先计算XLXT的特征值与特征向量，由特征向量可得U；然后用U对多光谱图像每个像元进行操作。当多光谱图像原始波段间的相关性较弱时，判别局部排列降维的第二步计算非常费时。

因此，本文在判别局部排列降维的基础上，提出新的优化波段选择方法，根据一定的准则，利用判别局部排列降维的结果，从原始波段中选择一组波段子集，既可保留多光谱图像原有的物理特性，又能显著缩短计算时间。如上所述，特征提取和特征选择算法同样作为降维算法用于模式识别和数据处理等领域，从高维数据中提取或选择特征对数据进行描述分析。特征提取算法在数据特征提取及描述方面有更优异的性能，而特征选择算法的特征结果有明确的物理意义，但常存在所选择特征无法对数据进行有效描述的缺点。本文提出选择基于权值和基于贡献率两种优化波段选择算法，从特征提取的角度对数据进行分析统计，并用光谱数据从提取特征的贡献量和贡献率的角度，分别对两种优化波段选择算法进行分析。

2.1 基于权值的优化波段选择算法

由特征提取U可知：特征提取的特征量本质是原波段加权和，因此权重信息的大小直接反映了当前各谱段对所提取特征的重要程度或贡献。显然，权重越大的谱段在所提取的特征中所占比重越大，说明其所包含更多对当前图像分类识别有效的信息，因此基于权值的优化波段选择算法期望从特征贡献权值的角度进行波段选择。设G=XLXT∈Rm×n，将G的特征值按从大到小的顺序排列λ1≥λ2≥…≥λm，分别对应特征向量Φ1，Φ2，…，Φm，则有

(8)

(9)

式中：φij为加权系数。

由式(9)可知：变换后原波段中X1，X2，…，Xm共m个波段的加权和即是第i个主特征的值，φij即是第j个波段Xj对第i个主特征的贡献的信息量，权值越大，说明信息量越大。则可定义Xj对前d个主特征贡献的总信息量为

(10)

可用权值绝对和的大小表示原始图像各波段所含重要信息量的大小，因此它能作为优化波段选择的判断标准。

2.2 基于贡献率的优化波段选择算法

上述基于权值的优化波段选择算法相对简单且计算量小，但它是通过直观的判断得出的结论，缺乏理论的支持。对此，本文基于文献[11]的贡献率概念，提出了另一种波段选择算法：依据贡献率的概念，分别分析当前各谱段有多少信息被映射到了特征提取算法提取的前d个主特征中，进而从贡献率的概念对各谱段包含的有效图像分类识别信息进行分析，并选取最优波段组合。

同样，由G的特征值按从大到小的顺序排列λ1≥λ2≥…≥λm，定义主特征Yk对原始数据的贡献率为

(11)

贡献率都为正值，则前d个主特征Y1，Y2，…，Yd对原始数据的累积贡献率为

(12)

定义主特征Yk与原来第i个波段Xi间的相关系数为

(13)

(14)

式中：k，i=1，2，…，N。易证明

(15)

则，前d个主特征Y1，Y2，…，Yd对原始数据第i个波段的贡献率vi是其与Xi的相关系数的平方和，即

(16)

同样，vi也能作为优化波段选择的判断标准。vi的大小反映了原始数据第i个波段被映射到了前d个主特征中的信息。

3 仿真实验

3.1 实验说明及算法流程

本文试验采用采集到的酒精灯和煤油灯火焰的光谱数据，共有谱段126个，数据立方体(x，y，λ)如图4所示，酒精灯和煤油灯火焰焰心区域的平均光谱如图5所示。实验目的是利用本文算法从光谱数据中提取能区分酒精灯跟煤油灯的波段。实验中采取交叉验证算法，利用图像中1%数据作为标签训练样本，其余99%数据作为测试样本，对本文提出的波段选择算法进行测试。选择支持向量机(SVM)分类器，交叉验证测试10次，取其平均输出结果作为测试结果。

图4 酒精灯与煤油灯的火焰光谱数据立方Fig.4 Spectral cuba of alcohol and kerosene lamp flame

图5 光谱曲线 Fig.5 Spectral curve

先设定目标区域，以区域内光谱点构成训练集合，分别用基于权值与基于贡献率的DLA优化波段选择算法对原光谱数据进行降维，选择特征光谱5个，同时兼顾能量损失，对选取的波段进行能量补偿以保证实际工程应用中的探测距离要求。算法流程如图6所示。

图6 算法流程Fig.6 Algorithm flowchart

3.2 实验结果

实验1：用本文的基于权值的优化波段选择算法对实验数据进行仿真。 选取部分酒精灯火焰上的点(25 580个)作为正样本，选取部分煤油灯火焰上的点(161 66个)作为负样本，取d=5，得到优化波段组合，组合波段号为[74，75，93，106，76]，相应的红外图像(图片大小为234×1 004)分别如图7(a)～(d)所示，图7(f)、(g)分别为用基于权值的优化波段选择算法提取的波段组合由SVM分类器对酒精灯和煤油灯火焰的识别结果。

图7 实验1结果Fig.7 Results of experiment 1

实验2：用本文的基于贡献率的优化波段选择算法进行仿真。用相同的训练样本，取d=5，得到优化波段组合[87，91，84，89，74]，各谱段红外图像如图8(a)～(e) 所示，用基于贡献率的优化波段选择算法所提取的波段组合，由SVM分类器对酒精灯和煤油灯火焰的识别结果分别如图8(f)、(g) 所示。

图8 实验2结果Fig.8 Results of experiment 2

实验3：用传统PCA算法降维进行仿真，选取相同的降维维度d=5，仿真结果如图9所示。

图9 实验3结果Fig.9 Results of experiment 3

(17)

表1 算法评价指标

由表1可知：与PCA算法相比，本文提出的两种算法同时根据正负样本进行降维，利用降维后的主特征区分酒精灯和煤油灯的准确率较高，计算时间显著缩短，且能保留原数据的物理特性，理解直观。

4 结论

鉴于PCA算法只能从正样本自身统计特性分析，而不能根据正负样本的可分性降维，且特征提取破环了原数据的物理特性，本文基于流形学习DLA算法，利用其对多光谱数据进行预处理，提出了基于权值和基于贡献率的两种优化波段选择算法，根据正负样本快速高效地选取优化波段，又保留原数据的物理特性。选择的优化谱段有助于对多光谱探测器的改进。本文利用特征提取的方法，提出了基于信息贡献权值和信息贡献率的两种波段优化选择算法。结合特征提取和特征选择算法，本文的波段优化选择算法可从波段对特征提取贡献的角度，快速选择对图像识别分类最有效的若干波段进行图像处理和识别。但目前本文算法仅从贡献率和权重信息的角度对信息进行描述和分析，后续研究将进一步对用信息熵等方法对信息进行更完善的描述和分析。

[1] 刘翔， 张晓杰， 郑翰清， 等. 复杂背景中红外多光谱目标检测算法研究[J]. 上海航天， 2016， 33(4)： 56-62.

[2] SERPICO S B, BRUZZONE L. A new search algorithm for feature selection in hyperspectral remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(7): 1360-1367.

[3] MELGANI F, BRUZZONE L. Classification of hyperspectral remote sensing images with support vector machines[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(8): 1778-1790.

[4] YANG H, DU Q. Fast Band selection for hyperspectral imagery[C]// Parallel and Distributed Systems (ICPADS), 2011 IEEE 17th International Conference on. Tainan: IEEE, 2011: 1048-1051.

[5] 周杨. 高光谱遥感图像波段选择算法研究[D]. 杭州: 浙江大学, 2014.

[6] 徐蓉, 姜峰, 姚鸿勋. 流形学习概述[J]. 智能系统学报, 2006, 1(1): 44-51.

[7] 夏威. 高光谱遥感图像的解混和波段选择方法研究[D]. 上海: 复旦大学, 2013.

[8] 杨金红. 高光谱遥感数据最佳波段选择方法研究[D]. 南京: 南京信息工程大学, 2005.

[9] ZHANG T, TAO D, LI X, et al. Patch alignment for dimensionality reduction[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(9): 1299-1313.

[10] 张田昊. 数据降维算法研究及其应用[D]. 上海: 上海交通大学, 2008.

[11] 赵选民, 徐伟, 师义民, 等. 数理统计[M]. 北京: 科学出版社, 2003: 308-314.

Algorithms Study for Selecting Few Characteristic Spectral Bands Based on Manifold Learning

GU Zhang-yuan1, LIU Xiang2, 3, SU Feng2, ZHENG Han-qing2, LIU Da1, LI Jian-xun1

(1. School of Electronic, Information and Electrical Engineering, Shanghai Jiao Tong University,Shanghai 200240, China; 2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China; 3. Infrared Detection Technology Research & Development Center,China Aerospace Science and Technology Cooperation, Shanghai 201109, China)

To implement the band selection algorithm from the feature extraction of multi-spectral image, and not only describe the data features but also remain the physical meanings of the selected bands, the optimization algorithm was studied based on manifold learning in this paper. Positive and negative samples were selected after a pretreatment on multispectral data by using discriminative locality alignment (DLA) algorithm. On the basis of the sample information, features were extracted to classify the targets. Using the feature extraction transformation matrix, the gross information content and contribution rate by the bands to the most discriminative and significant extracted features were analyzed and evaluated. Then the two algorithms based on weight and contribution rate, in which the features were selected based on weight as well as contribution rate respectively. The divisibility of the positive and negative samples can rapidly reduce dimension and retain the original physical features of multispectral image. The measured data proved that 5 spectrums could reserve the physical features of the original data after dimension reduction optimization. Meanwhile the target recognition rate increased by 2% and the calculation complex rate decreased by 50%. The optimization of band selection contributes to the development and application of the new generation multispectral detector.

multi-spectral; band selection; dimension reduction process; manifold learning; discriminative locality alignment (DLA) algorithm; characteristic; weight; contribution rate

1006-1630(2017)03-0040-07

2016-09-14；

2017-03-28

国家自然科学基金资助(61175008)；上海航天科技创新基金资助(SAST201448)

顾章源(1991—)，男，硕士生，主要研究方向为红外图像处理。

李建勋(1969-)，男，博士，教授，主要研究方向为多源信息融合与控制、智能信号与(红外)图像处理、稳健参数估计及在航空航天应用等。

TN216

A

10.19328/j.cnki.1006-1630.2017.03.005