三维交错沙波上的紊流特性数值模拟

何立群,陈孝兵,陈 力,赵 坚

(1.河海大学水利水电学院,江苏 南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)



三维交错沙波上的紊流特性数值模拟

何立群1,陈孝兵1,陈 力2,赵 坚1

(1.河海大学水利水电学院,江苏 南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)

为了揭示复杂河床沙波上的紊流结构特性,利用Fluent软件,基于雷诺平均N-S方程及k-ω紊流模型构建了描述三维沙波上水流运动规律的数学模型,并采用试验数据对模型进行了验证。结果表明:所采用的数值模拟模型能够良好的刻画沙波上的紊流特征,沙波的三维性是影响水流紊流结构的重要因素;相比于纵向相位差φ1,三维交错沙波的横向相位差φ2对剪切应力与床面阻力的影响更加显著,随着φ2增大,沙波逐渐交错,剪切应力与床面阻力均减小。

三维沙波;k-ω模型;紊流;剪切应力;床面阻力

沙波紊流结构的研究已取得了许多有价值的成果。毛野等[4]在循环水槽内利用粒子图像速度场仪将流动与电脑图像相结合,展示了沙波床面上紊流拟序结构;Noguchi 等[5]在运动沙波床面上测量了不同时间、不同床面位置的水流瞬时流速,认为波峰处的时均流速较明渠变化不大,波谷处由于反向流的作用,时均流速变化较大;陈孝兵等[6]利用NaCl示踪试验研究了不同床面形态驱动下的地表水-地下水水交换过程,认为近壁面流场分布是影响地下水流场的主要因素;黄华东等[7]以天然的阶梯-深潭结构为研究对象,采用k-ω紊流模拟方法探讨了不同流量条件下河床底部压力结构特性及安全性质;Stoesser 等[8-9]揭示出二维沙波表面的再附着点附近,流线弯曲并且向外运动会导致泡漩涡发展成发夹涡,他们将之归因于二次流的非稳定性;Venditti等[10-11]则统计了不同床面条件下水流分离区长度,得到分离长度大约为4～6倍波高的结论;Lefebvre等[12]则较为系统地讨论了不同二维沙波床面上水流分离现象与剪切应力之间的响应关系;唐立模等[13]对有关明渠紊流与床面形态的相互作用研究进行了分析和总结。

从已有的研究来看,无论是数值模拟还是物理模型试验,绝大多数研究集中在二维条件下,仅有极少数的研究涉及三维沙波情况,对于三维沙波条件下的紊流结构及动床阻力尚缺乏深入的研究。实际上,天然河流中沙波往往呈现为复杂交错的三维结构,且床面的三维性将引发水流的次生流,这在某些情况下可能会加强或减弱床面上的紊流强度。有限的研究已揭示出三维床面上的紊流结构明显有别于二维情况。Parsons等[14]通过分析Parana River底部沙波上的流速分布,讨论了不同沙波形态对水流的影响,结果表明，三维沙波与二维沙波相比,流速变化较大,其研究结果揭示了真实河流中不同沙波形态之间的紊流结构异同;Omidyeganeh等[15]利用大涡模拟方法研究了三维床面上流场结构,并分析统计了不同床面形态间紊流结构的差异,结果表明三维沙波流场中存在比二维流场更多的涡结构,三维床面增加了床面的水流拖曳力;Nezu 等[16]研究了沙波背水面的三维涡结构,发现分离涡的平均周期随雷诺数的增加而减小,泡漩涡的平均周期随雷诺数的增加而增加，泡漩涡的涡强度更大;Maddux等[2-3]通过在室内水槽中构建三维沙波来讨论二维、三维沙波形态的不同对流场分布以及沙波表面压力分布的影响,其试验研究方法为更进一步研究复杂三维床面上的水沙过程提供了宝贵的经验;最近,Chen等[17]在Maddux等[2-3]物理模型基础上,构建了三维沙波床面条件地形下数值计算模型,探讨了不同流动状态下床面阻力的变化规律以及床面压力分布状态和大小对来流条件的响应,并进一步分析了地表紊流对浅层地下水运动的影响,这一研究丰富了Maddux等[2-3]的物理模型研究成果。

总体而言,当前对于沙波上紊流结构的研究主要着眼于二维条件[4-8,17]或某一固定三维沙波情况,对沙波形态不断变化的情况下,河流紊流结构变化的规律性研究还亟待加强。本文针对复杂的床面沙波形态,基于数学模型,分析三维沙波规律性变化条件下相应紊流结构特征,探讨三维沙波变化对流场结构、床面阻力及剪切应力分布的影响规律。

1 模拟方法

1.1 控制方程

Patel等[19-20]对比了相同模型条件下,二维水槽试验与数值模拟中沙波上方流速分布、漩涡大小、阻力系数等表征参数,结果表明k-ω紊流模型对具有显著涡流结构的流动现象具有较好的适用性,能较好地刻画沙波上方紊流结构。

对于三维稳态不可压缩流,雷诺平均N-S方程为

=0

(1)

(2)

(3)

雷诺应力与紊动能k、比率耗散系数ω有关,其计算式为

(4)

其中νt=k/ω

式中δij为克罗里克符号。

紊流模型的k方程和ω方程分别为

(5)

(6)

其中μt=ρvtα=5/9β=3/40

β*=9/100σk=σω=1/2

1.2 模型说明

复杂的沙波河床地形结构会体现在沙波形态特征及其交错分布状况上。已有研究表明,天然河流交错沙波可以采用两组简谐波叠加生成,通过控制顺水流方向简谐波的纵向相位差φ1和垂直于水流方向的简谐波横向相位差φ2衍生出多种沙波结构[18]。图1(a)(b)(c)给出了3种典型的交错分布沙波形态。

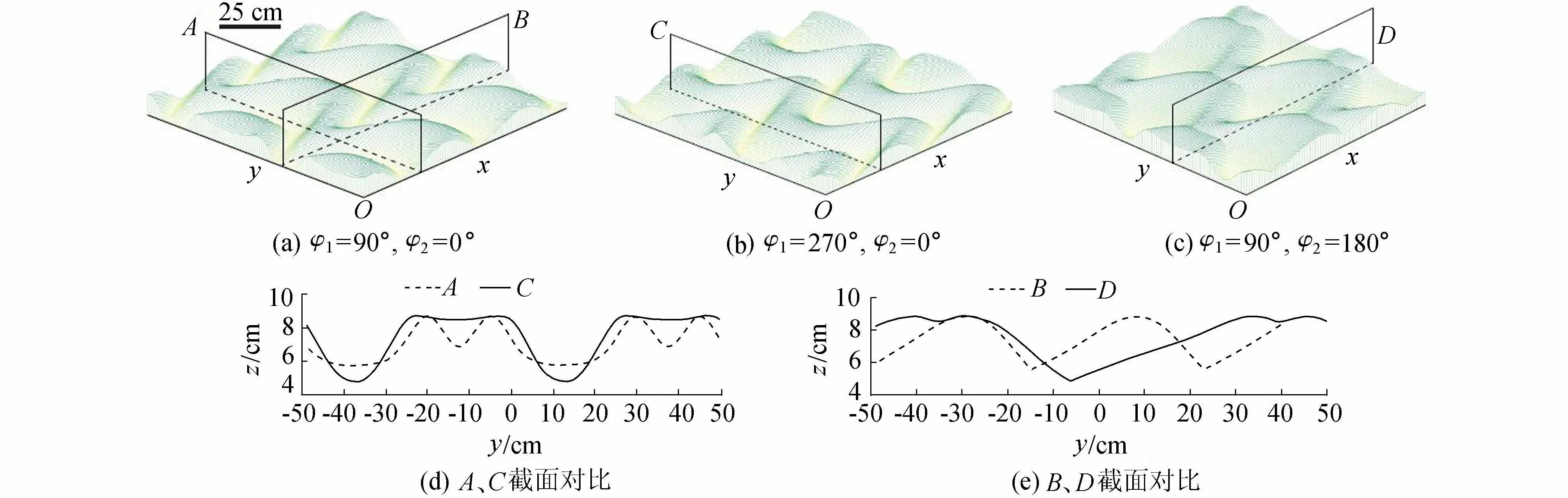
图1 部分典型沙波形态及φ1、φ2变化对沙波影响示意图

本文模拟中,φ1、φ2的变化范围分别为90°～270°和0°～180°,以30°为公差递增,不同的相位组合形成不同的沙波结构,共49个沙波模型,基本覆盖了沙波交错发展的各个阶段。图1(d)(e)描述了这两组相位差交替变化下,相应的床面结构变化情况,其中A、C与B、D分别为纵向 、横向波长中点处截面。不难看出,对比A、C截面,当φ1变化时,沙波基本形态保持一致,只改变相对高差;对比B、D截面,当φ2变化时,沙波由相互平行逐渐过渡到相互交错,床面基本形态发生改变;可见,床面的沙波交错式分布状况取决于横向相位差φ2。为了突出交错分布的床面对水流结构的影响,在模型中保持沙波单元横纵波长比以及波高为常量进行数值模拟计算,这一假定基本符合天然河流中沙波状态。

1.3 计算网格与边界条件

由于沙波在空间上具有一定的周期性和对称性,为了优化计算时间,对模型计算范围作如下考虑:对于每一种沙波地形,在纵向、横向上均截取一个周期作为计算域;在垂向上,选择远大于波高的水深值以保证波峰处截面上弗劳德数Fr≪1,水流为亚临界流条件,此时底部沙波对水流自由表面影响可以忽略[11]。图2为典型沙波模型及其边界条件,模型尺寸为0.76 m×0.5 m×0.5 m;边界条件设置为:水流左右两侧面为对称边界,底部为不透水边界,沿着水流方向的上下游边界为周期性边界,上下游边界之间的压力差为水流流动的唯一驱动力,水体顶面为光滑对称边界。利用GAMBIT软件进行网格划分,沙波表面设置34层边界层网格,第一层高0.1 mm,增长速率1.08倍,边界层网格厚度约为1.7 cm,边界层网格之上网格最小高度1 mm,最大高度2 mm(图2(a))。整个模型的单元数约为120万,经过网格独立性检验后,在此数量级的单元数下,解的精度不再因网格的进一步加密而有显著变化,满足计算要求,能较好地刻画沙波上方压力分布、背水漩涡、次生流等紊流结构特性(图2(b))。

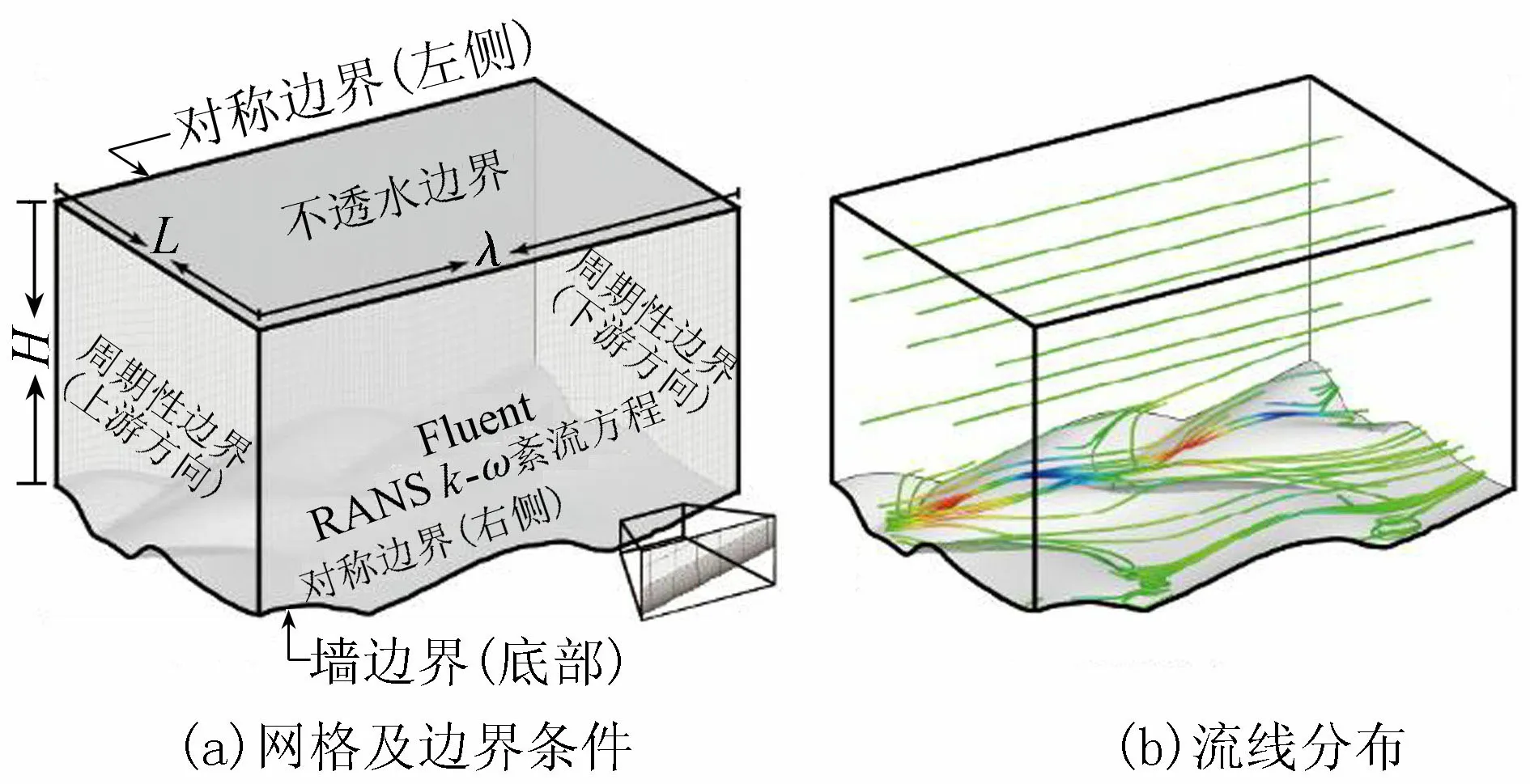
图2 模型网格、边界条件设置及典型流线分布示意图

2 模型验证

模型验证基于Maddux等[2-3]的水槽试验,试验采用的三维沙波尺寸为1.6 m×0.9 m,平均波高为0.04 m。选取其中T3工况的试验结果进行模型验证,该试验工况的平均水深为0.561 m,平均流速为0.261 m/s。通过设置相同的计算模型尺寸,采用上文所描述的边界条件设置和网格加密要求,通过人工调节进出口压力差,使水流平均流速接近水槽试验平均流速。通过对比相同截面上流速分布,来判断模型计算的合理性。模拟结果如图3所示,在沙波上方数值计算结果略大于试验结果,数值模型计算中能得到更大的背水漩涡。

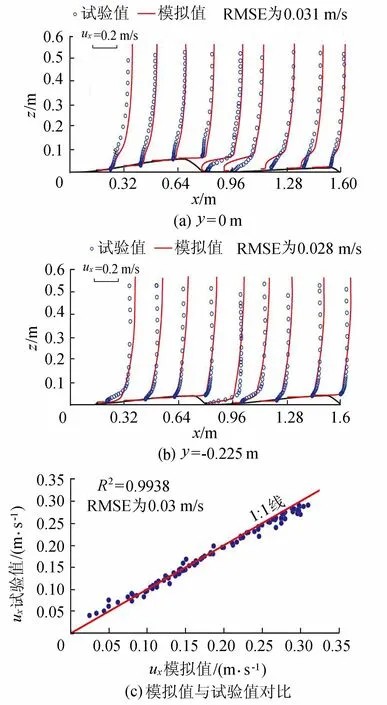
图3 两个不同截面流场试验及模拟流速结果对比

两个截面的流速均方根误差RMSE分别为0.031 m/s与0.028 m/s,远小于试验平均流速,得到的结果与试验结果比较吻合,采用的数值计算方法可靠。

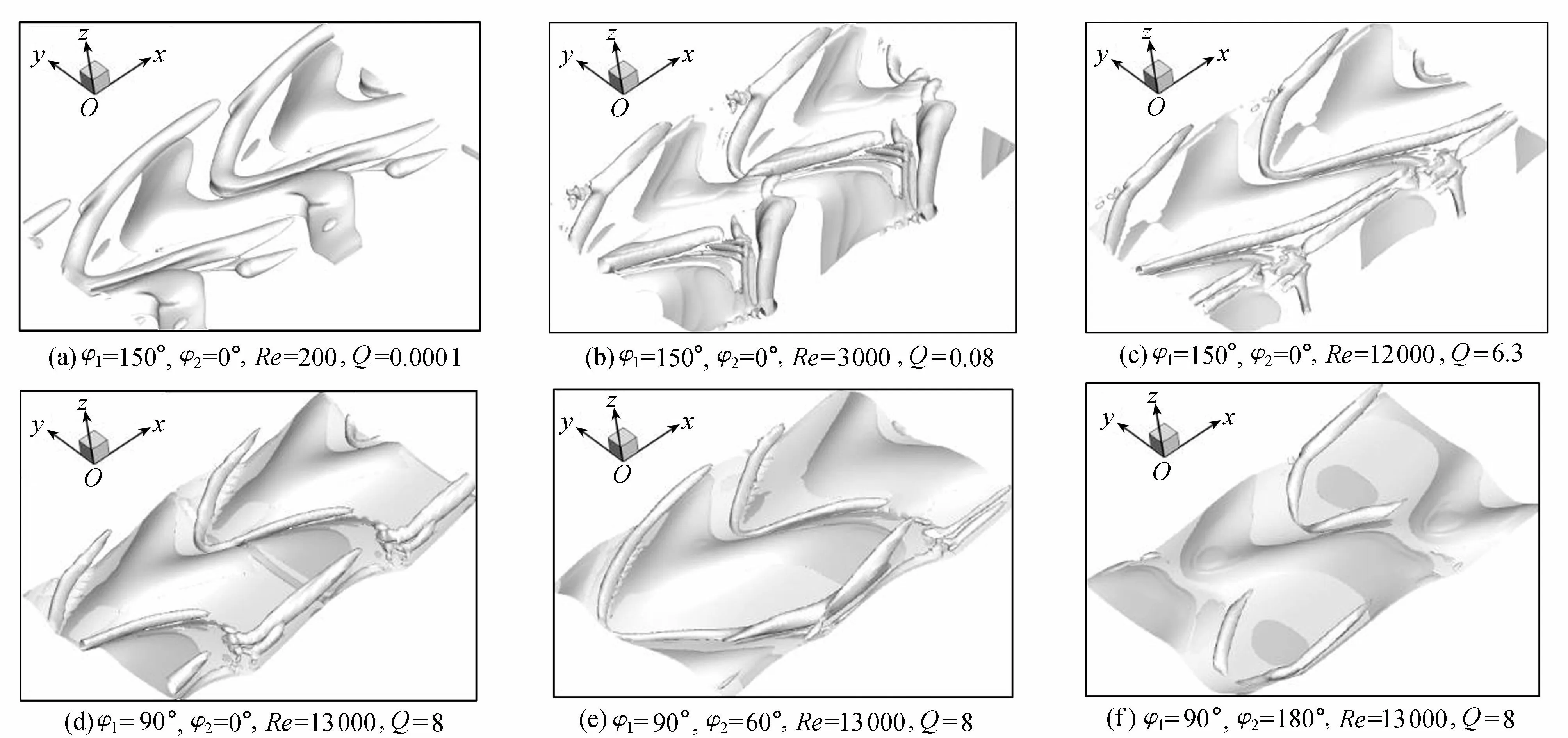
图4 不同雷诺数与沙波形态时涡量等值线

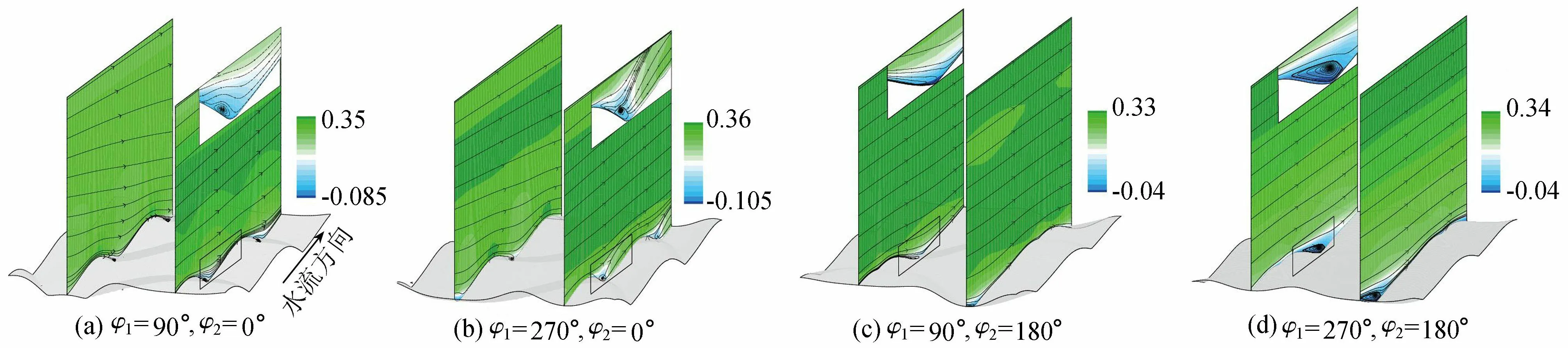
图5 xz剖面流线分布及x方向流速云图(单位：m/s)

3 结果分析与讨论

3.1 流场结构

通过分析床上涡结构、典型截面上的流场来探讨三维沙波上的流场结构；通过分析涡量等值面的分布情况及形态差异,可以非常直观的获得水流在近壁面处流动情况。定义雷诺数Re=Uh/ν,式中U为平均流速、h为沙波波高、ν为运动黏滞系数,图4给出了不同雷诺数和沙波形态下,涡结构等值面图。由图4可知,涡量等值面呈现两种形态:第一种为分布在波峰与波谷之间的管状结构,说明水流具有明显的漩涡结构;第二种为分离区附近的类平面结构,该区域流场结构变化剧烈,涡量变化明显。在沙波波峰上方流场结构受沙波形态影响较小,流线方向主要朝向水流方向,此处水流涡量较小;而在波峰以下近壁面区域,流场受沙波形态直接影响,剪切应力分布不均,水流呈现为绕流、漩涡等复杂的形态(图2(b))。

对比图4(a)(b)(c)可知,在相同沙波形态条件下,随着雷诺数增大,涡结构形态分布基本一致。剪切层在波峰处生成,并逐渐向下游扩散[18],因此波峰后涡结构较为复杂多变。同时,由于沙波的阻挡,部分水流沿着波峰线流动,与背水漩涡相结合,形成螺旋前进的三维绕流结构;部分水流则直接越过波峰线,形成水沙分离等紊流现象。对比图4(d)(e)(f)可知,随着φ2增大,连续的两个沙波由平行逐渐过渡为相互交错,由于沙波的阻挡,管状形态的涡量等值面减少,而由于沙波形态复杂度增大,近壁面处水流结构更为复杂,第二种形态的涡量等值面增多。

图5为相同雷诺数条件下,不同沙波形态中x方向流速分布云图以及流线分布。统计所有截面中分离区长度L,结果表明,L与波高h的比值范围为3.75～5.5。Noguchi等[5]实测了沙波形成各个阶段的水流特性,分析了沙波形态的影响,认为随着沙波的发展,分离长度增大,趋近于5.5 倍波高,本文的分析结果与其接近,略有差异的原因在于模拟过程中,模型尺寸、水流强度都不尽相同。

当φ2由0°增加至180°时,沙波逐渐交错,近壁面流态复杂,水流相互碰撞,逆流向水流受到限制,流速减小。因此,相比于图5(a)(b),图5(c)(d)整体流速分布均匀且x负方向流速更小。

图6为不同沙波条件下,yz剖面流线分布及y方向流速云图。在沙波上方,存在y、z方向流速矢量,这是由三维沙波导致的三维流动结构造成的。由于沙波阻力与主流区水体剪切力的共同作用,在波峰上方生成顺时针涡体,同时在波谷上方生成逆时针涡体。在波峰与波谷连接处,即为两种涡体交界处。

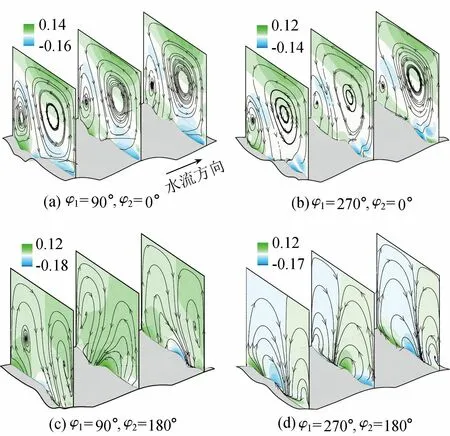
图6 yz剖面流线分布及y方向流速云图(单位：m/s)

对于图6(a)(b),顺时针涡体远大于逆时针涡体,占据整个截面的75%。原因在于波峰上方水体受沙波阻力影响较小,能量耗散较小,故流速矢量较大,而波谷上方水体则相反。对比图6(c)(d),随着φ2增大,沙波相互交错导致阻力减小,从而导致波谷上方逆时针涡体增大。由于两种涡体的相互作用,导致沙波上方水体y、z方向流速变化较小。

由图5、图6可知,沙波的三维性促成了流场中垂直、平行于流动方向的涡结构;可以预见,这种三维紊流结构将会影响床沙质纵向、横向的推移,沙波交错性与上覆水体流场分布具有很强的互动性。

3.2 雷诺剪切应力

雷诺剪切应力为

(7)

图7(a)(b)分别为不同φ1、φ2时,雷诺数与流场中最大剪切应力关系曲线。由图7可看出,剪切应力τ与雷诺数之间存在幂函数关系τ=aReb(式中a、b为系数,图7(a)中a=1.35×10-11,b=2.035),不同φ值对剪切应力影响不同。当φ2保持不变,φ1由90°增加到270°,Re=13 000时,(τmax-τmin)/τmin=15.7%。由于φ1变化并没有改变沙波形态的起伏度,当沙波波高一致时,波峰处的时均流速变化不大,故当雷诺数相同时,雷诺应力变化较小。

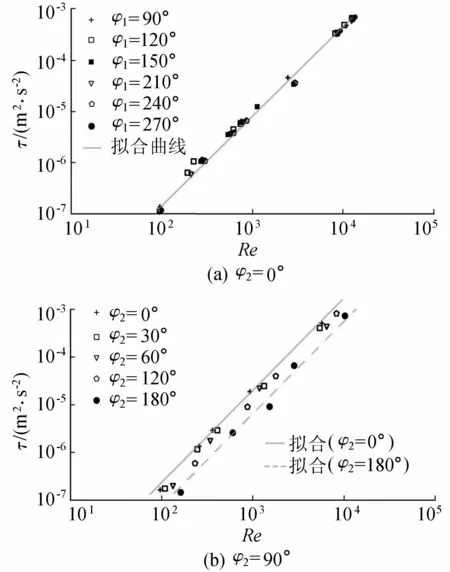
图7 雷诺数与剪切应力关系

图7(b)为沙波形态按φ2变化时,剪切应力变化规律,其中虚线的经验系数a=3.02×10-12、b=2.13,实线的经验系数与图7(a)一致。由图7可知,当雷诺数一致时,φ2增大,沙波逐渐交错发展,剪切应力减小,在曲线中表现为b≈2,但a随着φ2增大而减小。根据上文分析,沙波的交错发展导致上方流速分布均匀,故水流之间相互作用减小。

无论床面是否交错,最大雷诺剪切应力均分布在沙波背水坡上。水流越过沙波顶点后,沙波对流场的直接影响不复存在[4],由于没有沙波的作用,背水坡处流场结构很不稳定。如图4、图5所示,在背水坡处涡结构较为明显,流线复杂多变,说明流速变化剧烈,因此剪切应力较大。

3.3 沙波床面阻力

床面阻力大小直接影响河道泄流能力、输沙能力，对水位预报和河床变形预报十分重要。床面形态随水流强度变化而变化,而床面阻力又随床面形态的变化而变化。目前,对于沙波交错性所带来的床面阻力分布方面的研究极少。

图8给出了不同床面形态条件下总形状阻力与摩擦阻力分布趋势。显然,φ1变化对沙波的总形状阻力与摩擦阻力影响较小;而当沙波逐渐交错,即φ2增加时,摩擦阻力与总形状阻力均明显减小。总形状阻力与摩擦阻力的极大值与极小值分别出现在φ2=0°、180°时。这是由于沙波逐渐交错使得纵向截面上的沙波起伏度降低(参见图1(e)),对水流阻力干扰逐渐减小。

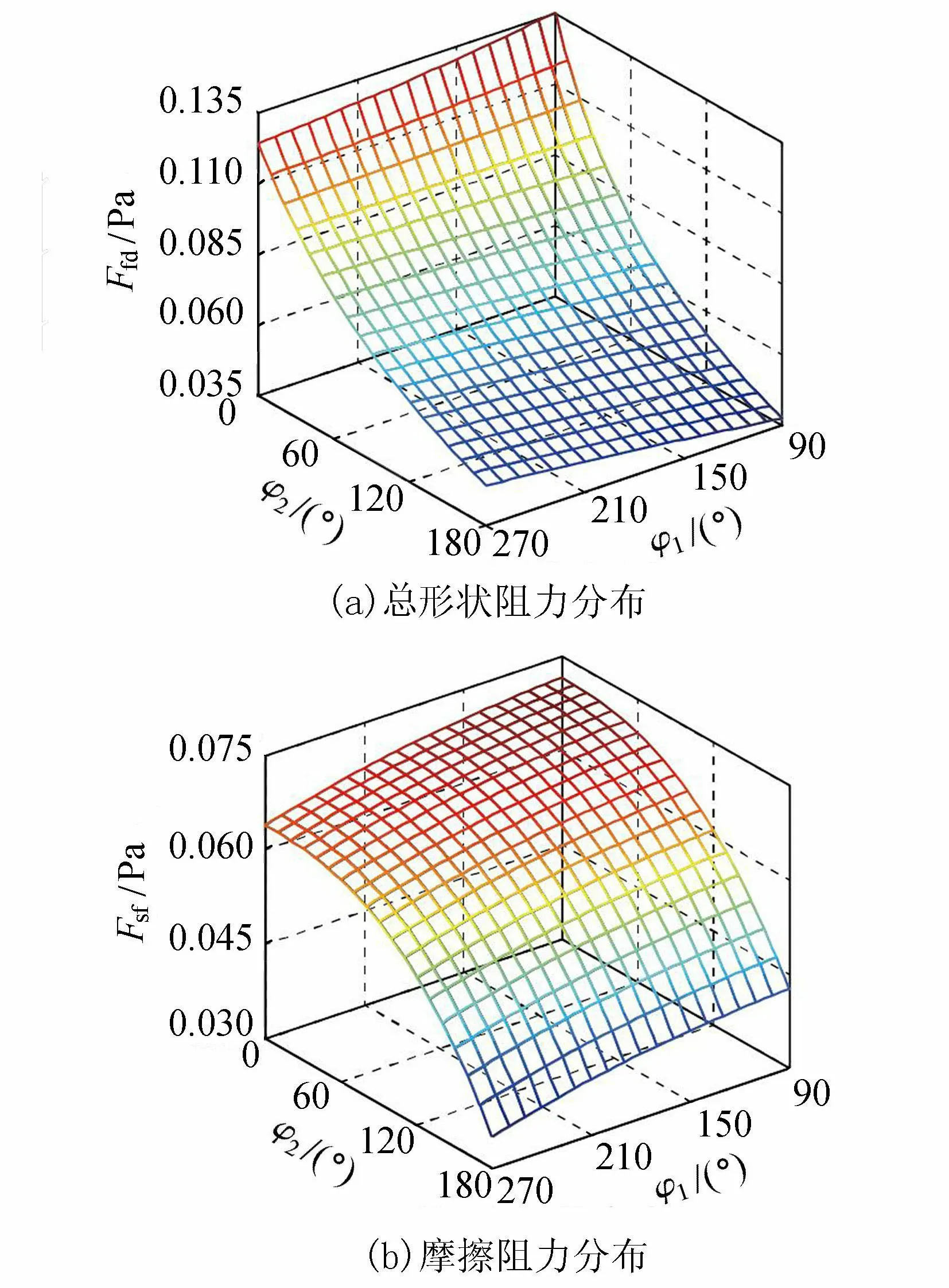
图8 不同床面形态下阻力分布

图8中的总形状阻力和摩擦阻力趋势面的最佳拟合公式分别为

Ffd=a/(1+bφ1+cφ2)

(9)

(10)

若取Re=6 000,式(9)系数为a=0.15,b=0.005,c=0.015,复相关系数R2=0.973;方程(10)系数为a=0.07,b=-6.82,c=-6.65,复相关系数R2=0.968。

4 结 语

基于雷诺平均N-S方程及k-ω紊流模型构建了描述三维沙波上水流运动规律的数学模型,试验结果表明，所建立的模型能准确刻画沙波上方水流运动特性。对模型交错性变化与近壁面流场结构、应力分布之间关系进行对比分析,结果表明:三维沙波的交错性是影响紊流结构的重要因素;在相同水动力条件下,流场最大剪切应力、床面阻力对φ1敏感性较低,φ2增大将使剪切应力与动床阻力减小。

本文仅着重对三维交错性沙波对水流影响做了分析讨论,而实际上沙波波高、波长等因素也是影响水沙运动的重要因素,今后需要进一步探讨更为复杂床面形态变化与近壁面紊流结构、泥沙输移之间的互动关系。

[ 1 ] PARSONS D R,BEST J.Bedforms: views and new perspectives from the third international workshop on marine and river dune dynamics (MARID3)[J].Earth Surface Processes & Landforms,2013,38(3): 319-329.

[ 2 ] MADDUX T B,NELSON J M,MCLEAN S R.Turbulent flow over three-dimensional dunes: 1.free surface and flow response[J].Journal of Geophysical Research: Earth Surface,2003,108(F1): 6009(1-10).

[ 3 ] MADDUX T B,MCLEAN S R,NELSON J M.Turbulent flow over three-dimensional dunes: 2.fluid and bed stresses[J].Journal of Geophysical Research: Earth Surface,2003,108(F1): 6010(1-11).

[ 4 ] 毛野,张志军,袁新明,等.沙波附近紊流拟序结构特性初步研究[J].河海大学学报(自然科学版),2002,30(5): 56-61.(MAO Ye,ZHANG Zhijun,YUAN Xinming,et al.Characteristics of turbulent coherent structures over sastrugi in open channels[J].Journal of Hohai University (Natural Sciences),2002,30(5): 56-61.(in Chinese))

[ 5 ] NOGUCHI K,NEZU I,SANJOU M.Turbulence structure and fluid-particle interaction in sediment-laden flows over developing sand dunes[J].Environmental Fluid Mechanics,2008,8(5/6): 569-578.

[ 6 ] 陈孝兵,赵坚,李英玉,等.床面形态驱动下潜流交换试验[J].水科学进展,2014,25(6): 835-841.(CHEN Xiaobing,ZHAO Jian,LI Yingyu,et al.Experimental study of bedform-driven hyporheic exchange[J].Advances in Water Science,2014,25(6): 835-841.(in Chinese))

[ 7 ] 黄华东,漆力健,余国安,等.阶梯-深潭结构潭底压力特征研究[J].长江科学院院报,2014,31(8): 50-54.(HUANG Huadong,QI Lijian,YU Guoan,et al.Characteristics of pressure at the bottom of step-pool[J].Journal of Yangtze River Scientific Research Institute,2014,31(8): 50-54.(in Chinese))

[ 8 ] STOESSER T,BRAUN C,VILLABA G,et al.Turbulencestructures in flow over two dimensional dunes[J].Journal of Hydraulic Engineering,2008,134(1): 42-55.

[ 9 ] 李佳佳,李志伟,张长宽,等.基于DANS方程的粗糙床面明渠水力特性研究[J].河海大学学报(自然科学版),2014,42(3): 217-222.(LI Jiajia,LI Zhiwei,ZHANG Changkuan,et al.Research on hydraulic characteristics of open-channel flow over rough bed based on DANS equations[J].Journal of Hohai University (Natural Sciences),2014,42(3): 217-222.(in Chinese))

[10] VENDITTI J G.Turbulent flow and drag over fixed two-and three-dimensional dunes[J].Journal of Geophysical Research: Earth Surface,2007,112(4): 1-21.

[11] LOPEZ F,FERNANDEZ R,BEST J.Turbulence and Coherent flow structures associated with bed form amalgamation: an experimental study of the ripple-dune transition[C]//Building Partnerships.New York: ASCE,2000: 1-10.

[12] LEFEBVRE A,PAARLBERG A J,WINTER C.Flow separation and shear stress over angle-of-repose bed forms: a numerical investigation[J].Water Resources Research,2014,50(2): 986-1005.

[13] 唐立模,孙会东,刘全帅.明渠紊流与床面形态相互作用研究进展[J].水利水电科技进展,2015,35(2): 77-84.(TANG Limo,SUN Huidong,LIU Quanshuai.Research development of the interaction between turbulence structure and bedforms in open channel[J].Advances in Science and Technology of Water Resources,2015,35(2): 77-84.(in Chinese))

[14] PARSONS D.R,BEST J.L,ORFEO O,et al.Morphology and flow fields of three-dimensional dunes,Rio Paran,Argentina: results from simultaneous multibeam echo sounding and acoustic Doppler current profiling[J].Journal of Geophysical Research: Earth Surface,2005,110(4): 1-9.

[15] OMIDYEGANEH M,PIOMELLI U.Large-eddy simulation of three-dimensional dunes in a steady,unidirectional flow:part 1 turbulence statistics[J].Journal of Fluid Mechanics,2013,721(4): 454-483.

[16] NEZU I,ADOTA A.Three dimensional structure of space time correlation on coherent vortices generated behind dune crest.[J].Journal of Hydraulic Researches,1999,37(1): 945-958.

[17] CHEN XIAOBING,CARDENAS M B,CHEN LI.Three-dimensional versus two-dimensional bed form-induced hyporheic exchange[J].Water Resources Research,2015,51(4): 2923-2936.

[18] RUBIN D M.Cross-bedding,bedforms,and paleocurrents[M].Tulsa:Society of Economic Paleontologists and Mineralogists,1987.

[19] PATEL V C,YOON J Y.Application of turbulence models to separated flow over rough surfaces[J].Journal of Fluids Engineering,1995,117(2): 234-241.

[20] YOON J Y,PATEL V C.Numerical model of turbulent flow over sand dune[J].Journal of Hydraulic Engineering,1996,122(1): 10-18.

Numerical simulation of turbulent characteristics over interlaced three-dimensional sand waves

HE Liqun1, CHEN Xiaobing1, CHEN Li2, ZHAO Jian1

(1.College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China; 2.State key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, China)

In order to investigate the structural characteristics of turbulent flow over sand waves on a complicated riverbed, a numerical model for simulating flow over three-dimensional sand waves was established using the Fluent software based on the Reynolds-averaged Navier-Stokes (RANS) equations and thek-ωturbulence model. The model was verified using experimental data. The results show that the established model can depict the turbulent characteristics over sand waves well. The three-dimensional properties of the sand waves are important factors influencing the turbulent structure of flow. The shear stress and bed form resistance are much more sensitive to the transversal phase differenceφ2than to the longitudinal phase differenceφ1. With the increase ofφ2, the sand waves become interlaced, and the shear stress and bed form resistance both decreased.

three-dimensional sand waves;k-ωmodel; turbulent flow; shear stress; bed form resistance

国家自然科学基金(41401014，51279045)；中央高校基本科研业务费专项(2016B03414)

何立群(1979—)，男，硕士研究生，主要从事潜流交换研究。E-mail:wwwhlq1@qq.com

陈孝兵(1985—)，男，副教授，博士，主要从事潜流交换研究。E-mail:x.chen@hhu.edu.cn

10.3880/j.issn.1006-7647.2017.04.004

TV131

A

1006-7647(2017)04-0019-06

2016-09-27 编辑：郑孝宇)