郑州市对商业地产需求的影响
摘 要:城镇化在推动经济增长,尤其是商业地产行业的增长方面起着越来越重要的的作用。本文首先根据郑州市1978年-2015年的城镇化率拟合了logistic增长曲线,然后对郑州市2016年-2020年的城镇化率进行了预测。然后证明了城镇化率与商品房销售面积之间的协整性并建立长期协整关系,接下来建立了两个时间序列的误差修正模型,并对2016年-2020年的商品房銷售面积做出预测。
关键词:城镇化;商品住宅需求;预测;logistic曲线;误差修正模型
一、研究基础
国内关于城镇化对商品住房的需求影响的研究,无论在理论上还是在实证上都已有了不小的成果。比如2002年曹光辉等采取逐步回归和组合预测分析方法构建了住宅需求总量预测模型,得出了住宅需求总量和城市人口呈正相关关系;2006年王峰等采用时间序列法对我国的城镇化进行预测,又根据刚性需求和改善需求确定了住宅市场需求总量模型,此模型可以确定特定时间区段的住宅市场需求总量;2009年在《中国城镇化对住宅销售量影响的实证研究》一文中,陈卫莉、曹华林,刘友平构建了城镇化和住宅销售面积构建了多阶分布滞后模型和自然对数模型对全国的住宅销售面积进行了预测。得出了1995年到2005年间中国城镇化率每提高1.4个百分点,住宅销售面积平均提高21个百分点,模型拟合度较好但使用数据较少;2010年在《城镇化对我国商业地产需求的影响》一文中,王文婷通过建立双对数一元线性回归模型,对我国商品住宅销售面积进行了预测,结果结果表明城镇化率每增加1个百分点,商业地产商品住宅销售面积增加5.2个百分点;2013年在《我国城镇化对商品住房需求的拉动效应研究》一文中,杨晓东、李远建立了误差修正模型,结果表明城镇化水平每提高1%,会拉动商品住房销售面积增长2.76%;2016年在《人口城镇化对河北省住房消费需求的影响》一文中用协整检验和格兰杰因果检验对比了城镇居民住房消费支出、城镇人口占比、商品房平均价格、人均GDP几组数据,发现人口城镇化、人均GDP、居民消费支出三者之间互为因果。
二、拟合logistic曲线并预测城镇化率
自然界中,很多事物的发展都有这样的规律:在发展初期,数量或规模增长缓慢,随后进入急速增长阶段,达到一定程度后,增长趋势又逐渐变慢,最终数量或规模不再增长,到达到一个稳定值。Logistic模型能很好的拟合这一事物增长规律。在社会学中经常被用于人口的增长预测、城镇化的增长预测。
1.Logistic方程模型简介及评价
Karmeshu研究发现,20世纪50年代以来发达国家随着经济发展水平的提高,城镇人口的增长相对农村要快一些,但是随着城镇化水平的提高,并趋向某一值时,速度将会减缓,城镇化水平的增长曲线大致表现为一条拉伸得“S”型曲线,城镇化率与时间变量表现为一种关系:U(t)=K/(1+a*exp(-r*t))其中U(t)表示城镇化水平,K为饱和城镇化水平,t为时间变量,a、r为待估参数。城镇化的饱和水平实际上与一个国家的城镇人口统计标准有关,当城市化水平达到最大值以后,城镇人口的比例会随时间推移在最大值附近波动。根据研究表明,Logistic模型中城镇化饱和水平K值可以取在80%以上,即K∈(0.8,1)。
2.指标选取及数据来源
在对城镇化进行研究的文章中,一般用城镇化率作为城镇化水平的指标。本文选取常住人口城镇化率作为城镇化水平的代表。数据是从郑州市统计信息官网人口统计部分得来。选取的是郑州市1978年-2015年的常住人口城镇化率作为研究对象。
3.模型建立
根据logistic方程:
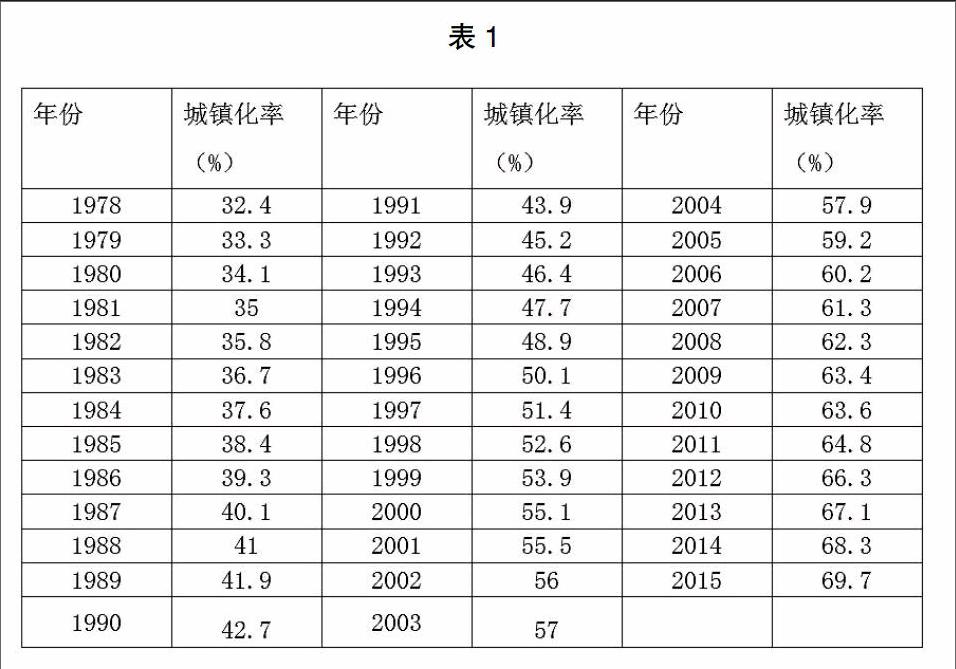
以郑州市1978年-2016年的城镇化率为时间序列,利用EVIEWS软件进行LS参数估计,拟合logistic曲线方程。表1为郑州市1978年至2015年的城镇化率。
将城镇化率设为Y,作为因变量。对年份做标准化处理作为t,自变量。然后建立YTC的logistic方程。由于K的取值在0.8到1之间,分别将K=0.8和K=1带入方程并进行参数估计。然后对2016至2020年的城镇化率进行预测。对取不同K值预测出来的估计量和原序列进行对比。发现当K=1所得出来的估计量和原序列数据更接近,,所以将K值定为1。
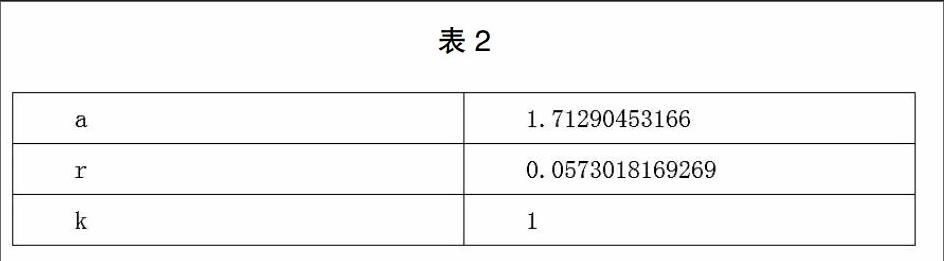
得出来的参数估计值为,如表2所示。
曲线方程为Y=1/(1+1.71290453166*EXP((-1)*0.057301816926 9*T))
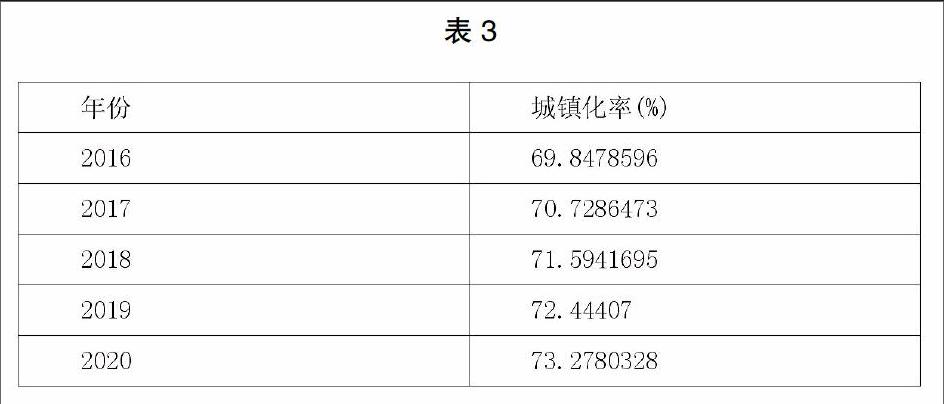
方程拟合优度检验R2=0.998363发现R2接近1,方程的拟合度为优,可以用此方程对城镇化率进行预测。由于至今为止郑州市信息统计网仍未公开2016年度的城镇化率,在这里本文对2016年的城镇化率也做预测。根据拟合方程对郑州市2016至2020年的城镇化率进行预测结果,如表3所示:
从预测结果来看,在2017年郑州市城镇化率会突破70%,之后几年会继续以0.8%至0.9%的幅度增长。
三、人口城镇化对住宅的影响及预测
选取城镇化率和商品住宅销售面积两个时间序列为自变量和因变量。用EVIEWS软件对两个序列进行ADF单位跟检验,检验两个序列的平稳性和协整性,并建立两个变量的长期均衡协整模型。
1.指标选取与来源
本文主要研究人口城镇化对商品住宅需求的影响,并试图建立一定的模型,进行定量分析及预测,从而更准确的把握郑州市商品住房需求。本文将城镇化水平作为解释变量,商品房需求作为被解释变量。而对住宅需求最直白明确的表现就是销售面积,所以将郑州市历年商品房销售面积作为因变量指标。对于城镇化水平,研究者一般用常住人口城镇化率来表现,所以本文用郑州市历年来的常住人口城镇化率作为自变量指标。
从表中数据可以看出,1999年至2007年,郑州市商品房销售面积持续增长增长幅度较大,而在2008年突然的下降,这根2008年的全球金融危机有一定关系。而在2009年开始则是有增有降,直至2015年销售面积达到1695.2万平方米。
2.序列平稳性检验及单整
检查序列平稳性的标准方法是单位根检验。有6种单位根检验方法:ADF检验、DFGLS检验、PP检验、KPSS检验、ERS检验和NP检验。本文将用EVIEWS软件对序列进行ADF检验。
由于X、Y两个指标的数值本身较大而且相差较大,所以先对X、Y进行对数化处理。对城镇水平和商品房销售面积对数化,得到LNX和LNY,用EVIEWS对序列LNX和LNY进行ADF检验。检验结果如表5所示:
检验结果发现LNX和LNY原序列都存在单位根,所以都不平稳。根据同阶单整理论接下来对LNX和LNY的一阶差分序列进行单位根检验。检验结果如表6所示。
根据检验结果,发现LNX和LNY的一阶差分序列都不存在单位根也就是序列平稳,也就是二者是同阶单整的。
3.协整关系检验
本文采用对残差序列进行ADF检验的方法来检验协整关系。利用ADF的协整检验方法来判断残差序列是否平稳,如果残差序列是平稳的,则回归方程的设定是合理的,说明回归方程的因变量和解释变量之间存在稳定的均衡关系。
用EVIEWS软件估计方程得到:
LNY=11.8306570757*LNX-42.3546568757 (方程1)
方程结果检验如表7所示
从结果看出DW=0.6,残差存在一阶自相关。可见所建立的协整模型方程1并不能很好的反映二者之间的影响关系。这个现象从实际情况来看是合理的。由于人口向城镇转移的过程中,需要一段时间才会对商品房销售面积产生影响,而有效需求并不是无限多的,前一期的商品房销售面积可定会对现期的产生消极的影响。
因此我们现将LNX和LNY的滞后期加入方程,用EVIEWS估计方程得到LNY=12.4887289996*LNX+0.659816673307*LNY(-1)-9.7376396236*LNX(-1)-9.17643224503 (方程2)
方程的检验结果如表8。
从结果看出R2=0.93方程拟合度较好,DW=2.13。当D-W值接近2的时候残差序列不存在自相关性。由于D-W值只能检验方程的残差序列是否存在一阶自相关,所以方程结果只能表明残差序列不存在强烈的一阶自相关,而要验证残差是否存在多阶自相关,需要用到L-M检验。接下来对方程进行LM检验观察残差是否存在高阶自相关。结果如下图所示:
LM检验原假设为:直到p阶滞后不存在序列相关,p为预先定义好的整数;备选假设是:存在p阶自相关。LM统计量显示,在5%的显著性水平接受原假设回归方程的残差序列不存在序列相关性。因此,方程2为关于城镇化率和商品住宅销售面积的协整方程模型,回归方程的估计结果有效。
4.误差修正及预测
误差纠正模型是一种具有特定形式的计量经济模型,基本思路为:若变量间存在协整关系,即表明变量间存在长期稳定的关系,这种长期稳定的关系是在短期动态过程的调整下得以维持。同时,存在某种联系方式把相互调整过程和长期稳定均衡状态结合起来。为防止长期关系的偏差在规模和数量上的扩大,任何一组相互协整的时间序列存在一种误差校正机制来反应短期调节行为。其具体过程为:在长期关系模型的基础上,将各变量以一阶差分形式进行塑造,并将长期关系模型产生的残差序列作为解释变量引入,在一个从一般到特殊的检验过程中,对短期动态关系进行逐项检验,不显著的项逐渐被剔除,直到最适当的表示方法被找到为止。
在做协整关系检验的时候已经得出了长期均衡关系方程:
LNY=12.4887289996*LNX+0.659816673307*LNY(-1)-9.737 6396236*LNX(-1)-9.17643224503 (方程3)
接下来短期动态调整模型:
令ECM=LNY-(12.4887289996*LNX+0.659816673307*LNY(-1)-9.7376396236*LNX(-1)-9.17643224503)。然后用ECM的滞后一期作为其中一个解释变量建立有动态调整项的误差修正模型。用EVIEWS软件根据最小二乘法估计参数,得到如下方程:
D(LNY)=2.84357967571*D(LNX)-0.444049186245*ECM(-1)+0.123711648944 (方程4)
由方程3和方程4可以看出,在长期情况下,郑州市城镇化率每增长1个百分点,商品住宅销售面积增长12.4个百分点。在短期,会以误差修正向量-0.44的的比例拉回均衡,城镇化率每增长1个百分点,商品房销售面积增长2.84个百分点。经调查研究发现,这种短期内的修正关系,是因为房价上涨的限制所形成的。在人口城镇化进程中,其中很大一部分刚性需要并没有成为有效需求。
参考文献:
[1]曹光辉,赵弊.重庆市主城区住宅需求总量预测模型[J].重庆大学学报,2002(25):22-25.
[2]王峰,王要武.“十一五”期间我国城镇化进程与住宅市场需求分析厂[J].一沈阳建筑大学学报,
[3]陳卫莉,曹华林,刘友平.《中国城镇化对住宅销售量影响的实证研究》[J].重庆工程学院学报,2009年第23卷第1期.
[4]王文婷.《城镇化对我国商业地产需求的影响》[J].兰州大学研究生院学报,2010年第9卷第4期.
[5]杨晓东.我国城镇化对商品住房需求的拉动效应研究[J].工程管理学报,2013第27卷第4期.
[6]任伟.《人口城镇化对河北省住房消费需求的影响》[J].河北联合大学学报,2016第16卷第1期.
作者简介:牛豆豆(1993.02- ),女河南开封人,郑州大学旅游管理学院2015级硕士研究生,管理科院与工程专业,研究方向:市场服务与营销

