基于希尔伯特-黄变换的直流微电网母线电压振荡检测

赵中田，胡 健，陈洪涛，刘澍存

(山东理工大学 电气与电子工程学院， 山东 淄博 255049)

基于希尔伯特-黄变换的直流微电网母线电压振荡检测

赵中田，胡 健，陈洪涛，刘澍存

(山东理工大学 电气与电子工程学院， 山东 淄博 255049)

直流母线电压稳定是直流微电网运行控制的目标之一，但由于直流微电网特殊的物理架构，易出现母线电压振荡现象.依据IEEE对电压振荡参数的规定，建立直流母线电压振荡信号的数学模型.考虑希尔伯特黄变换的模态混叠弊端，采用一种基于掩膜信号的改进希尔伯特-黄变换对母线电压振荡仿真信号进行检测.检测结果显示，该方法可以快速判断直流母线电压振荡的发生和结束时间，相对误差在0.378%以下，表明通过准确提取电压振荡信号的时频信息，希尔伯特-黄变换可实现对直流微电网母线振荡的检测与分析.

直流微电网;电压振荡;希尔伯特-黄变换;模态混叠;掩膜信号

新能源发电具有可再生、无污染和电能就地消纳等特性，是未来电能来源的主要形式之一.微电网是新能源发电接入配电网的一种重要形式[1-3].直流微电网系统不存在集肤效应问题，也无需控制频率稳定以及优化无功分布，因此在国内外得到日益关注和深入研究[4].由于直流微电网特殊的物理架构，其直流母线电压易发生振荡故障[5-6]，影响整个微电网系统的安全可靠运行.因此，对直流母线电压振荡进行准确的检测，对于快速消除故障、保障系统运行具有重要的意义.

目前，直流母线电压振荡信号的检测方法主要有傅里叶变换法、小波分析法、卡尔曼滤波法和希尔伯特-黄变换法等.傅里叶变换法是一种频域分析方法，当信号不满足狄利克雷约束时，傅里叶变换将失去作用.另外，傅里叶变换不适用于瞬时频率随时间变化的信号[7].小波分析法能够检测包含多个振荡频率的振荡信号，并可以消除信号附加噪声，得到信号的时频谱，但其检测结果受窗函数的影响较大[8].卡尔曼滤波法计算速度快，对信号的适应性好，但该方法不能反映出振荡的阻尼衰减特性[9].

希尔伯特-黄变换(Hilbert-Huang transform, HHT)由Norden E. Huang提出，是一种时频分析方法，可处理非线性和非平稳信号.该方法包括经验模态分解(Empirical Mode Decomposition，EMD)和希尔伯特变换(Hilbert Transform，HT)两个部分[10].HHT可依据信号的自身特征自适应分解信号.与傅里叶变换相比，HHT可检测非线性和非平稳信号；与小波变换相比，HHT不需要选择窗函数；与卡尔曼滤波法相比，HHT可反映振荡的衰减特性.因此，HHT法在检测直流母线电压振荡故障方面具有重要价值.文献[11-12]利用HHT方法对电压闪变、电压谐波等信号进行分析，得到电压波动的时频信息.由于HHT存在模态混叠弊端，文献[13]提出一种迭代改进的HHT方法，其可将混叠在一起的频率信息筛选出来，并通过仿真验证了此改进HHT方法的有效性和精准性.

本文首先采用标准HHT对母线电压振荡信号进行检测，结果显示间断弱信号导致的模态混叠问题将影响标准HHT法对振荡信号的检测精度.进而采用基于掩膜信号的改进HHT方法对母线电压振荡信号进行检测.结果比较显示，基于掩膜信号的改进HHT检测技术可有效检测直流微电网母线电压振荡.

1 直流微电网母线电压振荡成因分析

直流微电网由分布式电源、电力电子设备、储能单元和负载部分组成，通常采用单母线结构，如图1所示.直流母线由中性线N和正极线P构成，供电单元和负载单元均通过相应的电力电子设备与直流母线互联.直流微电网在输电阻塞、供电效率和投资成本上优于交流微电网，但是由于其特殊的物理架构，其直流母线易出现电压振荡问题.

图1 直流微电网网架结构

由图1可见，直流微电网中通常包含着大量的电力电子设备.其中，源侧变流器用于稳定母线电压，因此其通常工作在恒压模式下；负载侧变流器则工作在恒功率模式下，其与负荷可等效为恒功率负荷(constant power loads, CPL)[14].当直流微电网存在大功率恒功率负荷时，直流母线电压可能出现振荡现象[15].当网测变换器AC-DC工作在逆变状态向电网输送功率时，其滤波网络等效阻抗与配电网等效阻抗之间可能形成阻抗谐振网络.当逆变输出谐波存在时，可引发本体谐振.严重时，配电网中的其余并网逆变器与此网测变换器可形成交叉的局部谐振甚至全局谐振，严重危害直流微电网的稳定运行[16-17].另外，风机转速振荡、机械负载脉动和机械或电气故障均可引起负荷不平衡现象，此时直流母线电压也可能出现振荡问题[18].因此，直流微电网母线电压振荡的准确检测和有效抑制具有重要意义.

2 直流母线电压振荡的HHT检测技术

2.1 经验模态分解

振荡信号在任意时刻可能包含较多的振荡模式，HT不能描述此种信号的全部频率特性.因此，HT的应用受到一定限制，为避免这种不足，Norden E. Huang提出本征模态函数(Intrinsic Mode Function，IMF)的概念.EMD方法通过一系列的“筛选”过程将振荡信号分解为本征模态函数和残余信号之和.EMD方法分解步骤如下所示[10, 19].

(1)波形自适应匹配的端点延拓.

(2)求解信号s(t)的极小值与极大值.

(3)通过样条拟合，得到信号的上下包络线u(t)和υ(t)，上下包络线应满足υ(t)s(t)u(t)条件.

(4)计算上下包络线u(t)和υ(t)的均值曲线m(t)，即

(1)

(5)原始信号s(t)减去均值信号m(t)，求解第一个可能的IMF信号h1(t)，即

h1(t)=s(t)-m(t)

(2)

(6)查看h1(t)是否为IMF函数.若是，那么h1(t)即为第一个IMF函数C1(t)；若不是，则以h1(t)代替s(t)，重复上述2-5步骤，直到求解出第一个IMF的C1(t).

(7)计算第一个残余量.用原始信号s(t)减去第一个的IMF分量C1(t)，即

r1(t)=s(t)-C1(t)

(3)

计算残余量r1(t)是否满足EMD终止条件.若满足则终止EMD；若不满足，则对残余信号r1(t)重复上述2-7，并得到其余IMF信号C1(t)，直至终止条件满足，停止分解.

(8)最后原始信号可由有限个IMF信号和残余量信号叠加表示，即

(4)

2.2 希尔伯特变换

直流母线电压振荡信号通过EMD分解可得到有限个IMF函数，对IMF函数进行Hilbert变换，计算其瞬时频率和瞬时幅值，可得振荡信号在不同时间内含有的振荡信息.Hilbert变换定义为

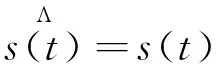
(5)

定义解析信号g(x)为

(6)

因此，可得信号g(x)的瞬时幅值、瞬时相位和瞬时频率分别为式(7)、(8)和(9).

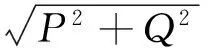
(7)

瞬时相位θ(t)=arctan(Q/P)

(8)

瞬时频率ω(t)=dθ(t)/dt

(9)

2.3 标准HHT法对直流母线电压振荡的检测

电压振荡是系统电压在稳定条件下，突发的一种非电源频率的，双极性电压变动现象，通常又分为低频，中频和高频振荡.根据IEEE的电压暂态振荡标准，低频振荡的振荡频率小于5kHz，故障典型持续时间在0.3ms～50ms之间，但对系统的危害通常最大[20].本文依据该标准构建直流微电网母线电压低频振荡数学模型如式(10).

u(t)=k+αe-γ(t-t1)[ε(t-t1)-

ε(t-t2)]·sin(λ2πft)}

(10)

上式中，k取值为400，即直流母线电压额定值为400V；母线电压振荡发生时刻设为t1=0.026 5s，结束时间设定为t2=0.030 0s，即振荡时间为3.5ms；α取值为20；γ取值为8；f取工频频率50Hz，λ取值为20，即模拟系统发生1kHz的低频振荡.因此，直流母线电压发生的振荡波形如图2所示.

图2 直流母线电压振荡信号

采用标准HHT对该振荡信号进行检测，得到EMD分解的本征模态函数如图3所示.本文所检测的直流母线电压振荡数学模型只包含一个振荡频率，因此IMF1信号为母线电压振荡部分.IMF2为一个虚假分量，由EMD分解的极点数小于3才终止的条件引起.振荡信号的时频图和幅值图分别如图4和图5所示.

图3 标准HHT的IMF

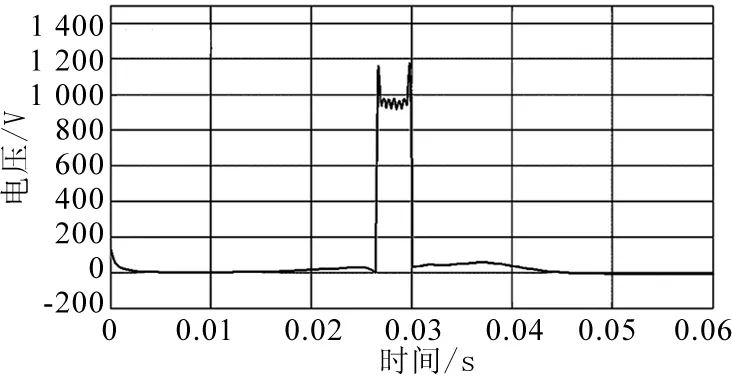
图4 标准HHT的时频图

由图3,4,5可见，标准HHT在处理间断弱振荡信号时存在的误差.图4的时频信息与模拟的仿真频率存在较大误差，在振荡突发时刻和结束时刻附近，振荡信号对0Hz频率的直流分量产生一定影响；故障时间内，检测出的频率小于实际的仿真频率.由于直流分量对振荡分量的影响，检测出的振荡幅值大于仿真信号的振荡幅值，如图5所示.因此通过仿真分析可知，标准HHT可实现对振荡信号的检测，但存在一定误差.因此，后文提出一种改进的HHT技术，提高HHT的检测精度.

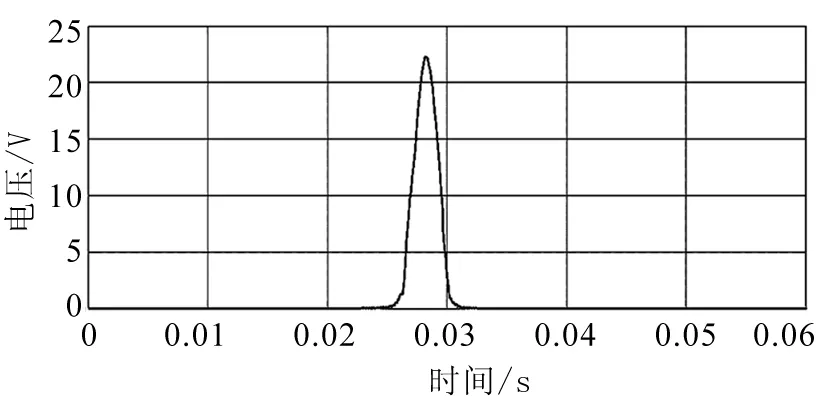
图5 标准HHT的幅值图

3 改进HHT技术及振荡检测流程

3.1 模态混叠及解决措施

Hung首先发现EMD分解过程中出现的模态混叠问题.模态混叠是指本征模态函数的频率并不唯一，其主要由三个原因导致：(1)噪声混入信号，导致原信号的极值点发生改变；(2)复分量信号中，各个单模信号的频率过于接近；(3)信号中存在间断弱信号干扰.母线电压振荡EMD的模态混叠问题即是由间断的振荡分量干扰而导致的.

本文采用掩膜信号法对原信号进行改进，可获得单一频率的IMF分量.掩膜信号法通过构建掩膜信号X(t)，对原始信号进行处理.令

S+(t)=S(t)+X(t)

(11)

S-(t)=S(t)-X(t)

(12)

对(11)、(12)分别进行EMD分解，得到相应的本征模态函数，因此可得原信号的IMF为

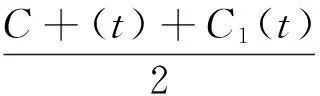
(13)

本文通过信号的短时傅里叶变换估测复合信号包含的可能频率分量F，并依据短时傅里叶变换的幅频特性，求得信号在频率分量F下的幅值M，最终构建掩膜信号X(t)=Msin2πf

3.2 电压振荡检测流程

本文将通过对直流微电网母线电压振荡信号的检测，验证改进的HHT检测方法的有效性，检测流程如图6所示.

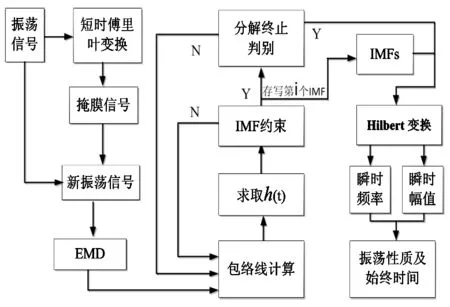
图6 HHT检测电压振荡流程

3.3 改进HHT对母线振荡的检测

采用掩膜信号改进的HHT对式(10)所示的振荡信号进行检测，得到EMD分解的本征模态函数如图7所示.对比改进HHT和标准HHT的IMF1信号可知，改进之后的HHT可精确提取振荡弱信号.改进的本证模态函数IMF1分量表征了原始信号的物理意义，即在母线电压发生振荡时刻，IMF1出现低频振荡信息.对IMF分量进行希尔伯特变换，得到振荡信号的时频图和幅值图，如图8和图9所示.

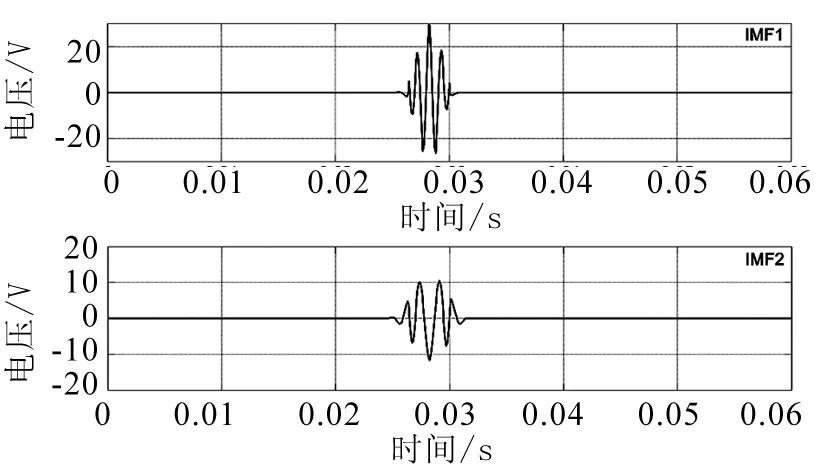
图7 改进HHT的IMF

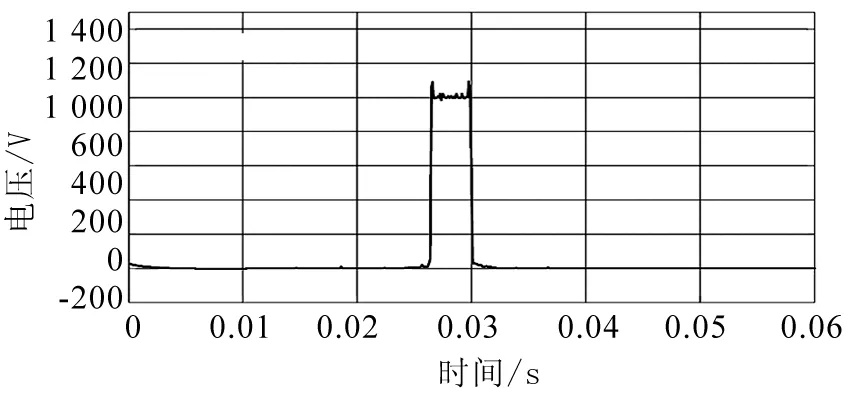
图8 改进HHT的时频图

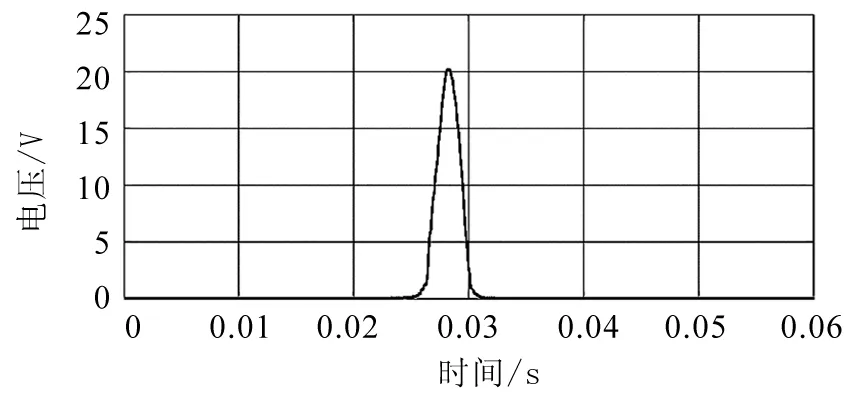
图9 改进HHT的幅值图

对图8进行分析，可得由于母线电压突然发生振荡和振荡突然消失，对信号的频率产生较大冲击，因此信号频率出现两个较大的突变；在母线电压振荡时刻内，母线电压振荡频率为1kHz，与本文设定的振荡频率相统一；在其余正常时刻，母线电压频率为0Hz.对比标准HHT的时频信息可知，标准HHT在故障突发时刻和结束时刻不能较准确的反映出故障的瞬时特性，并且检测出的振荡频率存在较大误差，而改进的HHT则明显的提高了检测性能.通过分析图8时频图中频率的两个冲击点，可得故障发生时刻为t1=0.026 6s，振荡结束时间为t2=0.029 9s.仿真结果与实际设定的故障发生与结束时刻误差小，相对误差在0.378%以下.由于直流分量的影响，标准HHT得出的IMF幅值存在较大误差.通过改进HHT分解出的IMF振荡幅值为20V，如图9所示，与本文设定一致.因此，通过仿真验证了改进HHT在检测直流母线电压振荡信号方面的有效性和精确性.

4 结束语

考虑希尔伯特黄变换的模态混叠问题，采用掩膜信号的改进方法，对原始信号处理，以提高信号EMD分解的准确性.通过改进希尔伯特-黄变换对仿真信号的检测，得出信号的时频信息，检测出电压振荡的发生和结束时间，并且得出母线电压振荡频率，明确电压振荡性质.结果表明，通过提取电压振荡信号的时频信息，希尔伯特-黄变换可实现对直流微电网母线电压振荡的检测与分析.

[1]TOMISLAV D, LU X, JUAN C, et al. DC Microgrids—Part II: A Review of Power Architectures, Applications, and Standardization Issues[J]. IEEE Trans Power Electron, 2016, 31(5): 3 528-3 549.

[2] ZHAO Z T, HU J, LIU J X. Hierarchical coordinated control of multi bus-based DC microgrid considering fault occurred in buses[C]//CSEE. Proceedings of 2016 China International Conference on Electricity Distribution. Xian: Chinese Society for Electrical Engineering， 2016: 1-6.

[3]郭兆琪,胡健,边敦新，等. 利用风电机组改善农村配电网电压质量[J]. 山东理工大学学报(自然科学版), 2016, 30(63)-66.

[4] HOSSEIN L, AMIN K. AC Versus DC Microgrid Planning [J]. IEEE transactions on smart grid, DOI: 10.1109/TSG.2015.2457910.2017,8(61):296-304.

[5] 赵文龙,徐丙垠,哈恒旭，等. 考虑极端情况的分布式电源对配电网保护影响评估方法[J]. 山东理工大学学报(自然科学版), 2014,28(05):1-5.

[6] STANLEY R H, JOSEPH D S. Amplitude Death Solutions for Stabilization of DC Microgrids With Instantaneous Constant-Power Loads[J]. IEEE Trans on Power Electronics, 2013, 28(1): 247-253.

[7] MOHAMMAD J A, DANNY S, DAVID S. Analysis of Nonstationary Power-Quality Waveforms Using Iterative Hilbert Huang Transform and SAX Algorithm[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2 134-2 144.

[8] RINKI G, ARUN K, RAJENDAR B. Estimation Of Instantaneous Frequencies Using Iterative Empirical Mode Decomposition[J]. Signal, Image and Video Processing, 2014, 8(5):799-812.

[9]杨德昌, REHTANZ C, 李勇，等. 基于改进希尔伯特-黄变换算法的电力系统低频振荡分析[J]. 中国电机工程学报, 2011, 31(10): 102-108.

[10] NORDEN E H, WU Z. A Review On Hilbert-Huang Transform: Method And Its Applications to Geophysical Studies[J]. Reviews of Geophysics, 2008, 46(2): 1-23.

[11] 江辉,王晓强,彭建春. 基于希尔伯特-黄变换的电压闪变测量方法[J]. 电网技术, 2012, 36(09): 250-256.

[12] 费丽强,李鹏,李晓春，等. 基于HHT变换的微网电压闪变与谐波检测新技术[J]. 电网与清洁能源, 2011, 27(11): 9-12，19.

[13] DRUMMOND C. F, SUTANTO D. Classification of Power Quality Disturbances using the Iterative Hilbert Huang Transform[C]//ICHQP. Proceedings of 14th Int. Conf. Harmonics Quality Power. Bergamo: Department of Energy and the Department of Electrical Engineering of the Politecnico di Milano, 2010: 1-7.

[14] 李玉梅,査晓明,刘飞. 含有多个恒功率负荷的多源直流微电网振荡抑制研究[J]. 电力自动化设备, 2014, 34(3): 40-46.

[15] ALEXIS K, CHIMAOBI N, ONWUCHE K. Dynamic Behavior and Stabilization of DC Microgrids With Instantaneous Constant-Power Loads[J]. IEEE transactions on power electronics, 2011, 26(3): 822-834.

[16] 陈鹏伟,肖湘宁,陶顺. 直流微网电能质量问题探讨[J]. 电力系统自动化, 2016, 40(10): 148-158.

[17] WANG X, FREDE B, WEIMIN W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6 421-6 432.

[18] EHSAN J, BABAK N, PHILIPPE P, et al. Distributed Active Resonance Suppression in Hybrid DC Power Systems Under Unbalanced Load Conditions[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1 833 -1 842.

[19] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J], Proc Roy Soc Phys Eng, 1998, 454: 903-995.

[20]肖湘宁，电能质量分析与控制[M], 北京：中国电力出版社，2004: 7-11.

(编辑：刘宝江)

Oscillation detection for bus voltage of DC microgrid based on Hilbert Huang transform

ZHAO Zhong-tian, HU Jian, CHEN Hong-tao, LIU Shu-cun

(School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255049,China)

One of the aims for microgrid operational control is to maintain the stabilization of DC bus voltage. However, the oscillation existence of bus voltage cannot be easily eliminated owing to the special physical architecture of DC microgrid. According to the IEEE provisions on voltage oscillation, the mathematical oscillation signal model of DC bus voltage is established. An improved Hilbert Huang transform with masking singal is adopted to detect the oscillation of DC bus voltage simulation signal. The starting and ending time and end of the voltage oscillation can be quickly detected, and its relative error is below 0.378%. The time-frequency information has accurately been obtained by Hilbert Huang transform applied to this signal, which has verified that Hilbert Huang transform can realize the measurement and analysis for DC microgrid bus oscillation.

DC microgrid; voltage oscillation; Hilbert-Huang transform(HHT);mixed frequency; masking singal

2016-11-17

赵中田，男，zztianor@126.com; 通信作者: 胡健，男，hujian@sdut.edu.cn

1672-6197(2017)05-0060-05

TM7

A