三维修正SPH方法实现的海水运动效果模拟*

欧训勇，陈美伊，鲍海琴，康小平

(海南热带海洋学院 海洋信息工程学院，海南 三亚 572022)



三维修正SPH方法实现的海水运动效果模拟*

欧训勇，陈美伊，鲍海琴，康小平

(海南热带海洋学院 海洋信息工程学院，海南 三亚 572022)

围绕SPH的标准控制方程，对SPH的标准核函数使用了所谓的线性再生核近似方法进行修正，这种方式所取得的梯度效果令人满意。修正的SPH方法模型用来模拟流体自由表面运动。仿真效果展现了水平面上波的形成和传播过程。最后在OpenGL环境下实现了的逼真模拟效果。

SPH；自由表面流体；流体运动

0 引言

光滑流体动力学方法(以下称为SPH)是1977年由Lucy、Gingold和Monaghan率先提出的，至今该方法已经得到了广泛的研究及应用，并成为通用性和有效性最强的应用于物理、力学、工程等领域计算离散粒子的方法之一。SPH方法成为有重要意义的计算方法可以归因于它几个突出的优势：概念简单、容易编程实现、处理大变形问题。作为一种无网格的纯拉格朗日方法，SPH方法已成功应用于一系列现象的数值模拟，如动态冲击、金属损伤和断裂、海浪运动、传热过程、水下爆炸等。

当然，SPH方法也被用来解决各种流体力学问题，包括有重要的水文现象和离岸工程等。例如，文献[1]中运用这一方法研究水上的重力流和孤立波；文献[2]中分析了在一个垂直墙面和倾斜的海滩上的孤立波运动过程；文献[3]研究了经典的溃坝问题，包括水撞击墙体的分析；文献[4-5]使用SPH方法研究了物体入水等自由表面流动问题；文献[6]研究利用SPH方法模拟了二维和三维波浪在倾斜的海滩上的破碎问题；文献[7]利用SPH研究了弹性流体结构相互作用的问题；文献[8]利用不可压缩流的SPH方法研究流体自由表面运动的模拟过程。

以上所提到关于对于流体力学问题的研究，SPH方法的各种变体已经应用到了很多领域之中。早期的研究成果中，有代表性的，例如文献[1]中，传统的SPH方法是以水作为一个弱可压缩流体[1]，和其中所有的场变量利用一个单一的插值函数(称为SPH光滑核)，在其作用域内近似离散成粒子。在后来的研究文献中，不断提出各种改进的方法，以实现更好的真实流体建模，并加强了计算的准确性[4-5]。本文提出一种修正的SPH方法模拟海水自由表面运动。

1 控制方程

本文中，把水视为一个可压缩的粘性液体，并假设它的运动发生在等温条件下，完全是由重力引发的运动。流体质量守恒的连续方程如下：

(1)

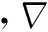
(2)

式中，p是流体压力，b指的是外力，本文所指的外力在没有其他作用力时其实就是重力。如果考虑其他力，那么b就是这些力和重力之和。

假设流体受正压，在这种情况下，压力是由流体密度唯一确定。根据传统的SPH方法，压力p和密度之间的变化规律如下：

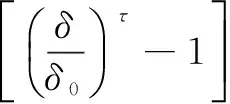
(3)

式中，P0和δ0压力和密度的参考值，参数τ的取值如果为水流体是7，为空气则1.4。相应地，声音的速度表示为：

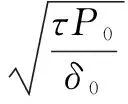
(4)

方程(3)的突出作用是表明了压力和密度的直接关系，这就使得没有必要解决任何额外的压力方程(这是不可压缩流的泊松方程)。因此，快速显示的时间步长算法可以在计算中采用，避免在泊松方程的影响下使用隐式方法。

2 SPH理论和方程

在SPH方法中，任何系统都认为是由一套随意离散分布的粒子构成的，每个粒子都承载相关的物理信息，如：质量、密度、动量、温度等。由于粒子分布是离散的，独立运动，因此该方法具有完全无网格的特征。场变量是通过特定的插值函数来近似的，这就是光滑核。这些函数表述了给定空间或质点的场量值。通常核函数由限定域的非零函数构成，这个限定域称为支持域。设x为位置矢量，a和b为两个粒子，场函数f(x)在粒子a处的取值由核函数W以粒子a为中心近似估算取得。由于核支持域的紧支性，只有位于这个域内的粒子才有被插值累加。其方程如下：

(5)

式中，fb=f(xb)是粒子b的离散值，Vb是粒子b的体积，N是核支持域内的粒子数。

光滑核W是带两个参数的函数，r是两粒子a和b之间的距离，计算式子为：

(6)

h是核的光滑长度，取决于支持域的大小和核插值粒子数的离散量。

核函数的表示有多种形式，使用最为广泛的核函数有高斯核函数、三次样条函数、五次样条函数。本文讨论的SPH方法使用的是三次样条核函数，其形式如下：

(7)

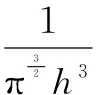
2.1 SPH标准方程

为了导出给定问题域的离散方程，需要微分算子离散近似，SPH方法中有几种方法用来构造函数梯度和微分算子的近似计算。文中使用MONAGHAN JJ提出的计算公式[1]，计算某粒子a的标量场函数的梯度，其近似的插值公式如下：

(8)

类似地，粒子a的矢量场函数的散度计算公式为：

(9)

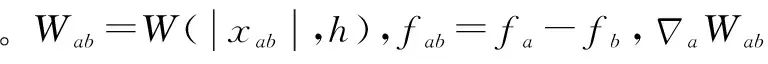
(10)

式(10)是核函数W的在粒子a处的梯度计算式。由于式(7)是对称的，因此Wab=Wba，式(10)有如下关系：

(11)

将式(1)和式(2)用式(8)和式(9)的离散形式表示，可得计算形式如下：

(12)

(13)

2.2 修正的SPH方法

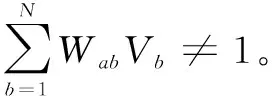
(14)

(15)

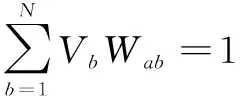
式(14)中的系数cαβ(x)(α,β=1,2,3,4)是由应用完整条件的插值函数及它们的导数确定的，这些函数由BELYTSCHKOT等人于1998年推导出[9]。由这些条件构造的矩阵方程为：

AcT=I

(16)

式中，c为系数cαβ构成的矩阵，I为单位矩阵，经过变换A的表达式为：

(17)

在三维中，上述的修正过程要求对每个粒子a生成矩阵A及反演。利用式(14)～(16)可计算求得系数c，将修正的核函数及梯度代入式(12)～(13)得到修正核函数后的动量守恒方程。

3 SPH方法的时间步积分

数值求解的问题可以利用以下一组一阶微分方程来取得：

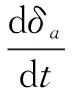
(18)

式中，Ma和Fa遵从质量守恒和动量守恒定律。根据式(12)和(13)的离散形式，利用修正的核函数及梯度，这两个场量的新的计算式子如下：

(19)

(20)

式(18)中的第三个方程中的Ua是粒子a的速度修正量，该变量值采用Monaghan提出的公式进行求取：

(21)

式中，粒子a的速度是通过位于粒子a的支持域内的所有临近粒子b的光滑处理平均值。利用这一做法，可以防止粒子间相互渗透，和传统的SPH方法对比更能确保粒子有序和有规律的运动。根据文献[1]，式(21)中ε取值在0和1之间。

式(18)中方程组的数值求解是应用显式时间步的典型的预估校正类型，每个时间步分两个阶段计算。设tk和tk+1是两个瞬时时间点，时间步长度为Δt=tk+1-tk。第一个计算阶段在tk+1/2=(tk+tk+1)/2，计算取得粒子的密度、速度和位置，其计算规律如下：

(22)

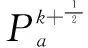
第二个计算阶段，t=tk+1，其计算规律如下：

(23)

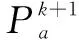
4 SPH方法的边界和初始条件

在搜索粒子a的临近粒子时，使用链式算法。计算范围中空间区域按照匹配的支持域划分为网格间距。显然地，每个粒子仅与它四周相邻的八个粒子存在相互作用的关系。只要有四个相邻的粒子已经处理过，那就没必要把八个相邻的粒子都进行搜索。这样一来就把搜索算法的时间复杂度从O(N2)降到O(NlogN)的级别。当光滑长度为常量时，使用链表能取得最佳效果。本文使用文献[6]提出的动态边界条件。边界粒子与流体粒子具有相同的行为，遵循连续性、动量守恒和状态方程。而不同的是，流体粒子有位移行为，而边界粒子的位移为零。

当有粒子到达边界时，边界的粒子密度增加。因此，由于运动方程中的压力作用，流体粒子的受力增加。当边界粒子和流体粒子的距离变小，受排斥作用，流体粒子的密度、压力和作用力增加。

5 程序运行结果

根据以上各节介绍的方程及数值求解的过程，利用OpenGL三维图形库[10]，在MS Visual Studio 2010环境下，使用C++面向对象的编程方法实现了对广阔海面上划浪航行的浪涌效果模拟。此程序算法对实现海上航行模拟海浪冲击船舷及轮船破浪行驶都有相当大的价值。考虑到计算量，SPH程序使用粒子数总量为12 000个，即为12k。粒子质量为0.000 205 43，密度为400，光滑核长度为0.012，粒子半径为0.04，粒子影响间距为0.005 9，流体黏度系数为0.8，时间步长度为0.004程序运行效果截图如图1所示。

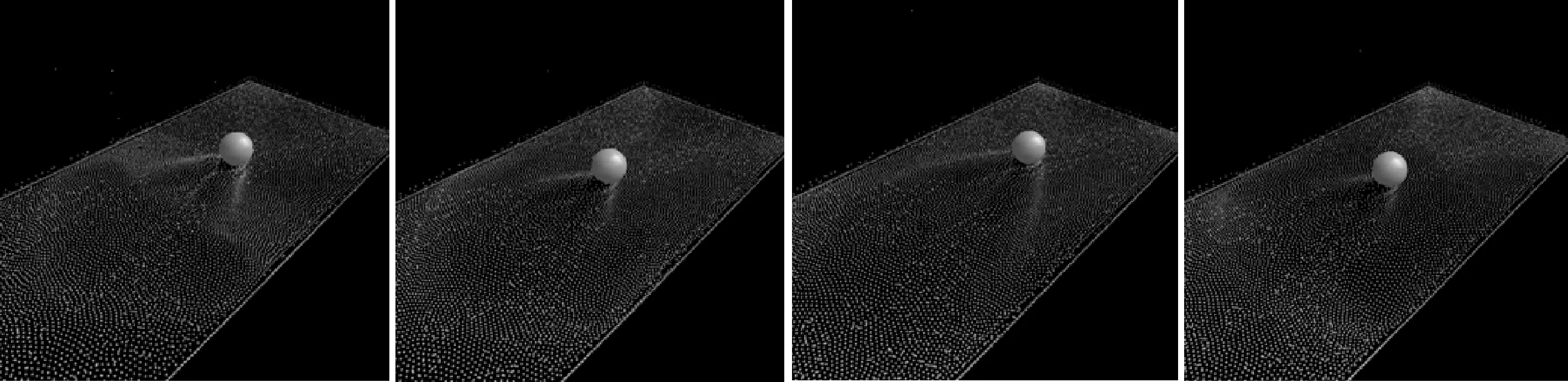
图1 程序运行截图

6 结论

程序运行在CPU为Intel(R) Core(TM) i3-2348M@2.30 Hz，内存为4 GB的计算机上模拟的海浪效果非常流畅。以上方法实现的算法SPH粒子数量可达20 000个以上。超过20 000个粒子后，看到模拟动画效果就出现卡顿了。要想达到更大的粒子数量，采用GPU方法能取得更佳效果。本研究在应用于构建模拟大水域海浪运动，将继续深入探索GPU方法及网络分块协同渲染描绘更大水域波浪运动。研究成果将应用于构建在光滑粒子流体动力学方法下的船舶运动的虚拟仿真系统。

[1] MONAGHAN J J. Gravity currents and solitary waves[J]. Physica D: Nonlinear Phenomena, 1996,98(2-4):523-533.

[2] LO E Y M, Shao Songdong. Simulation of near-shore solitary wave mechanics by an incompressible SPH method[J]. Applied Ocean Research, 2002,24(5): 275-286.

[3] COLAGROSSI A, LANDRINI M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J]. Journal of Computational Physics, 2003,191(2): 448-475.

[4] 龚凯. 基于光滑质点水动力学(SPH)方法的自由表面流动数值模拟研究[D].上海:上海交通大学，2009.

[5] 郑坤. 基于SPH方法的波浪对水平板冲击作用研究[D]. 大连:大连理工大学，2009.

[6] DALRYMPLE R A, ROGERS B D. Numerical modeling of water waves with the SPH method[J]. Coastal Engineering, 2006,53(2-3): 141-147.

[7] ANTOCI C, GALLATI M, SIBILLA S. Numerical simulation of fluid-structure interaction by SPH[J]. Computers and Structures, 2007,85(11-14): 879-890.

[8] ATAIE-ASHTIANI B, SHOBEYRI G, FARHADI L. Modified incompressible SPH method for simulating free surface problems[J]. Fluid Dynamics Research, 2008,40(9):637-661.

[9] BELYTSCHKO T,KRONGAUZ Y,DOLBOW J,et al.On the completness of meshfree particle methods[J]. International Journal for Numerical Methods in Engineering,1998, 43(5): 785-819.

[10] 张立成，张鸽.一种OpenGL局部缩放算法及应用[J].微型机与应用，2013，32(19)：44-47.

Simulation of seawater motion based on a 3D modified SPH method

Ou Xunyong, Chen Meiyi, Bao Haiqin, Kang Xiaoping

(School of Marine Information Engineering, Hainan Tropical Ocean University, Sanya 572022, China)

In this paper, around the standard control equation of SPH, the so-called standard linear reproducing kernel approximation method is used to modify the standard kernel function of SPH. And the gradient effect obtained in this way is also satisfactory. The model of the modified SPH method is used to simulate the fluid motion. The simulation results show the formation and propagation of the waves on the horizontal plane. Finally in the OpenGL environment it achieves the realistic simulation.

SPH; free-surface fluid; fluid motion

海南省自然科学基金项目(20166226)

TP311.1

A

10.19358/j.issn.1674- 7720.2017.12.021

欧训勇，陈美伊，鲍海琴，等.三维修正SPH方法实现的海水运动效果模拟[J].微型机与应用，2017,36(12)：71-74.

2016-12-20)

欧训勇(1976-)，男，硕士，副教授，主要研究方向：OpenGL三维图形技术、虚拟现实技术。

陈美伊(1980-)，女，硕士，实验师，主要研究方向：数字媒体及应用。

鲍海琴(1982-)，通信作者，女，硕士，实验师，主要研究方向：环境工程。E-mail：573835681@qq.com。