基于改进的传递矩阵法的滑动轴承动态标高的快速计算方法
毛文贵,曾 毅, 黄中华,李建华, 王高升
(1.湖南工程学院 机械工程学院,湘潭 411104;2.湖南工程学院 湖南省风电装备与电能变换协同创新中心,湘潭 411104; 3.湘电风能有限公司,湘潭 411102)
基于改进的传递矩阵法的滑动轴承动态标高的快速计算方法
毛文贵1,2,曾 毅3, 黄中华1,2,李建华1, 王高升1
(1.湖南工程学院 机械工程学院,湘潭 411104;2.湖南工程学院 湖南省风电装备与电能变换协同创新中心,湘潭 411104; 3.湘电风能有限公司,湘潭 411102)
大型旋转机械滑动轴承-转子系统含有多个滑动轴承,为静不定结构,滑动轴承各标高变化对滑动轴承载荷、性能以及机组安全运行的影响很大.提出了基于传递矩阵法快速获得滑动轴承动态标高的计算方法.对Riccati传递矩阵法进行改进,修改了典型单元的状态向量,获得整个轴系的状态方程.引用文献中四个滑动轴承支撑的滑动轴承-转子系统作为算例验证了该方法的精确性.
滑动轴承-转子系统;动态标高;动态载荷;改进的Riccati传递矩阵
滑动轴承—转子系统在工程实际中常由多个滑动轴承支撑,处于超静定状态.滑动轴承安装时为了使滑动轴承—转子系统各个联轴节处于弯矩为零的理想状态,各滑动轴承的轴心的垂直方向的高度不同.即存在静态标高.实际工作过程中由于油膜作用轴心的位置处于变化状态使轴承承受动态载荷,从而存在动态标高.静态标高是滑动轴承—转子系统初步设计时确定的.动态标高使滑动轴承载荷分布偏离于设计时计算的静态载荷分布,有可能因为其不合理而造成转子失稳.因此,快速获取滑动轴承的动静态标高对滑动轴承—转子系统提高机组的稳定性具有重要的理论和工程意义.研究者对于轴系动态特性的研究考虑了轴承配置和标高的影响[1-4],在轴系分析方法方面也进行了很多探索性的工作,如结构修正法、传递矩阵法、有限差分法和有限单元法等[5].传递矩阵法因矩阵的阶数不随系统的自由度增大而增加,编程简单占内存少,运算速度快,对于转子这样的链式系统有突出的优点而占主导地位[6-7],Riccati传递矩阵法因可消除奇点的干扰而在转子动力学的振动计算中被广泛采用.本文考虑轴系为有质量轴段,以外力的形式引入滑动轴承油膜力,对Riccati传递矩阵法进行改进,获得应用于计算滑动轴承-转子系统的挠度和载荷的传递矩阵.并基于改进的Riccatii传递矩阵法获得滑动轴承的动态标高和动态载荷.
1 改进的 Riccati 传递矩阵法
转子一般由多个滑动轴承支撑.转子系统的静态标高及载荷分布计算方法已经较成熟.但实际运行中的转子系统由于轴承油膜的作用,存在着动态高标,从而轴承承受的是动态的载荷分布.为了得到作用在每个轴承上的真实载荷,一般采用迭代算法,本文采用传递矩阵法提取结构的参数.
Riccati传递矩阵法分析轴系结构时对系统进行离散化处理.离散成一系列简单力学特性表示的集总圆盘、轴段类的二端元件.每个元件端面上的位移和力以列状态向量表示.本文中因考虑结构的自重,轴段为有质量轴段.滑动轴承油膜力等效为作用于转子轴段上的外力.因此,在轴系的集总圆盘处应考虑外力的加入,在集总圆盘上加入集中力Qo和力矩Mo.根据传递矩阵法的研究方法,考虑本文轴系的自身特点,建立滑动轴承—转子系统模块化图如图1所示.
集总圆盘表示为第i结点和第i+1结点,联接第i结点和第i+1结点为第i场,无滑动轴承支撑的称为外结点,其包括的几何质量属性为:质量m、直径转动惯量Jd、极转动惯量Jp.有滑动轴承支撑的称为内结点,还包含滑动轴承的刚度和阻尼系数矩阵K、C.无质量轴段的场的几何属性为:外径D、内径d和轴长L.结点和场的状态向量剪力Q和弯矩M分为左右两端,以上标R和L表示.

图1 滑动轴承—转子系统模块化图

不改变传递矩阵的计算原则,为使传递矩阵具有通用性并方便建立整体矩阵,本文将状态向量的维数扩为5.状态向量变为:
(1)
其中:My为弯矩, Qy为剪力,wy为位移,θy为转角.
1.1 有质量轴段的场传递矩阵
参阅文献[8]中关于主轴段处于静态时有质量主轴段y方向左右两端的弯矩、剪力、转角和挠度等状态变量关系,在本文中引入变形系数V来考虑自然轴段的剪切影响中的扭转变形,对于图1中一个质量自然轴段i左右两端进行受力分析,公式(2)所示.
(2)
联立公式(2)和公式(1)则一个有质量自然轴段的两个自然结点之间的状态关系为公式(3):
(3)
其中:
Z为自然结点的状态向量;

a为截面系数(实心圆轴为0.886,空心圆轴为2/3);G为剪切弹性模量;E为弹性模量;
A为截面面积;L为自然轴段的长度;
J为自然轴段的截面惯性矩.
如果一个主轴段有s个理想轴段,则相邻两个集总圆盘间有质量主轴段的传递关系为公式(4).反映滑动轴承-转子系统有质量轴段左边状态向量挠度、转角、弯矩、剪力传到右边状态的传递关系.
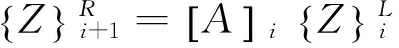
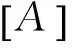
(4)
式中:A为有质量主轴段的场传递矩阵;
B为有质量自然轴段的场传递矩阵.
1.2 集总圆盘的点传递矩阵
由于集总圆盘不仅具有质量,而且具有转动惯量,转动时将产生陀螺力矩.对于图1中一个集总圆盘i左右两端进行受力分析,分析集总圆盘左右两端所受的剪力和弯矩,并考虑集总圆盘上有滑动轴承支撑,如公式(5)所示.
(5)
联立公式(5)和公式(1)则集总圆盘两侧截面的状态参数之间的关系可表示为公式(6):
(6)
其中:
m为集总圆盘的质量;Ω为自转角速度;ω为进动角速度.
1.3 典型单元的传递矩阵
把主轴段和集总圆盘综合为一典型单元,计算典型单元的从左边状态到右边状态的场传递矩阵为公式(7).
(7)
获得每个典型单元传递矩阵后,离散为N个结点组成主轴系统N-1个典型单元传递矩阵相乘可得整个轴系的传递矩阵方程为:


(8)
式中:H为典型单元的传递矩阵;
T为轴系的传递矩阵.

2 动态标高和动态轴承力
当轴不旋转时,滑动轴承为刚性支撑,可根据每个滑动轴承的静态标高获得轴承力.而当轴旋转时,滑动轴承为弹性支撑,转轴始终浮动在轴承油膜上,转轴的中心轴线相对静态标高曲线偏离了一定的距离,转轴中心线在动态标高曲线上,与各时刻的偏心率和偏位角有关.动态标高的计算公式如式(9).已知滑动轴承的偏心率和偏位角,可参照文献[9,10,11]求解雷诺方程获得对应偏心率和偏位角下滑动轴承的轴承力.也可查阅相关的滑动轴承设计手册利用插值法获得相应偏心率和偏位角下滑动轴承的轴承力.
(9)
式中:w为动态标高;h为静态标高;R为滑动轴承的半径;r为轴颈的半径;ε为偏心率;θ为偏位角,n为滑动轴承个数.
公式(9)中的偏心率和偏位角是静平衡时滑动轴承的偏心率和偏位角,其值预先是不知道的.计算时要预先假定,如果假定正确,则按式(9)获得的是滑动轴承的真实动态标高.在这一动态标高下,每个滑动轴承都工作在各自的静平衡位置.类似于滑动轴承为刚性支承.其下一刻的静态标高即为此时刻按公式(9)得到的动态标高.但一般情况下假设偏心率和偏位角是不正确的.为得到作用在各个滑动轴承工作状况下的真实载荷,一般采用迭代算法.滑动轴承的动态标高和动态轴承力的计算流程如图2所示.
先计算静态标高下各刚性支承轴承受的静态负载;再根据各轴承的负载确定各轴承静平衡的偏心率和偏位角;由公式(9)获得各轴承的动态标高,获得此动态标高情况下轴承的动态载荷.比较静态和动态载荷之间的关系直到满足公式(10),则可获得这一时刻滑动轴承动态标高和动态载荷.

图2 动态标高及轴承动态载荷计算流程
滑动轴承动态载荷的收敛条件:

(10)
3 数值验证
应用文献[12]中四个滑动轴承以1000 mm跨距支撑一个长为3000 mm的轴段的滑动轴承-转子系统为算例,检验本文的方法.轴段的直径为0.1 m, 密度为7800 kg/m3,杨氏弹性模量为210 GPa,滑动轴承为圆柱轴承,其参数为:长径比为0.5,间隙比为2‰,油的动力粘度为0.0184 N·s/m2.各轴承的静态标高相同(处于零标高状态),转速为3000 r/min下各轴承的动态标高及动态载荷计算结果如表1所示.本文解与文献的计算结果误差都很小.而且迭代过程收敛很快,具有良好的工程应用价值.

表1 轴承动态标高和载荷的计算结果
4 结论
工程中多个滑动支撑处于超静定状态的转轴系统,快速准确获得动态标高和动态载荷是提高轴系提高机组的稳定性的重要因素.本文考虑轴段为有质量轴段,以外力的形式引入滑动轴承油膜力,对Riccati传递矩阵法进行改进,将状态向量的维数扩为5,修改了典型单元的状态向量,获得整个轴系的状态方程.提出基于改进的传递矩阵法和迭代法获得滑动轴承动态标高和动态载荷,通过经典算例进行检验,精度高且时间短.
[1] 魏艳辉,苏 秦,曹 兴.转子系统轴承标高对载荷影响实验研究[J].电站系统工程,2016,32(5):15-16.
[2] 马 斌,张志谊.艉轴承标高对轴系横向振动的影响理论分析[J]. 噪声与振动控制, 2015,35(6):56-60.
[3] 杨国栋.低压轴承标高变化对600MW空冷机组轴系动特性影响研究[J]. 机械工程师, 2014,(11):237-238.
[4] 顾卫东,王永亮,方 勃,等.标高对转子一滑动轴承系统动力学特性影响研究[J].汽轮机技术,2011,53(2):125-128.
[5] Yuzhong Cao, Y.Altintas. Modeling of Spindle-Bearing and Machine Tool System For Virtual Simulation of Milling Operations [J]. International Journal of Machine Tools & Manufacture, 2007, 47:1342-1050.[6] MBDeepthikumar, AS Sekhar, MR Srikanthan.Balancing of Flexible Rotor With Bow using Transfer Matrix Method [J]. Journal of Vibration and Control, 2014, 20(2): 225-240.
[7] 张世东,杨建刚,朱先宝,等.应变-传递矩阵法计算轴系载荷分布及实验研究[J].动力工程学报, 2012,32(7):513-516.
[8] 刘鸿文.材料力学[M]. 北京:高等教育出版社.2016.
[9] 毛文贵,李建华,王高升.滑动轴承-转示系统的轴心轨迹分析及优化[J].湖南工程学院学报(自然科学版),2016,26(2):14-18.
[10]肖忠会,王丽萍,郑铁生.滑动轴承油膜力Jacobi矩阵的一种快速算法[J].应用力学学报,2005(1):67-70.
[11]戴惠良,刘思仁,张 亮. 滑动轴承油膜压力的新算法[J].机床与液压,2011,39(11):27-28.
[12]徐龙祥.高速旋转机械轴系动力学设计[M].北京:国防工业出版社,1994.
An Efficient Method for Calculating Dynamic Elevation of Sliding Bearing Based on Improved Riccati Transfer Matrix Method
MAO Wen-gui1,2,ZENG Yi3,HUANG Zhong-hua1,2, LI Jian-hua1, WANG Gao-sheng1
(1.College of Mechanical Engineering, Hunan Institute of Engineerning, Xiangtan 411104, China; 2.Hunan Province Cooperative Innovation Center for Wind power Equipment and Energy Conversion, Hunan Institute of Engineering, Xiangtan 411104, China; 3. XEMC Wind Power Co., Ltd, Xiangtan 411102, China)
There are multiple sliding bearings for large rotating machinery, which is a statically indeterminate structure. The influence of sliding bearing elevation change on the change of bearing load, bearing dynamics and the safe and reliable operation of units is great. An efficient method for calculating dynamic elevation of sliding bearings is proposed based on the improved Riccati transfer matrix method, in which the state vector of a typical element is modified. The Riccati transfer matrix program for a sliding bearing-rotor system can be obtained and the proposed method is applied to a typical sliding bearing-rotor system with four sliding bearings. The results are compared with the literature to verify the effectiveness of the proposed method.Keywords:a sliding bearing-rotor system; dynamic elevation; dynamic load; improved riccati transfer matrix method
2016-11-27
湖南省自然科学基金资助项目(2016JJ6026);湖南省教育厅科研资助项目(15B057);湖南省高校科技创新团队支持计划资助项目(湘教通〔2014〕207号).
毛文贵(1975-),女,博士,副教授,研究方向:转子动力学,现代设计理论与方法.
TH113.3;O322
A
1671-119X(2017)02-0024-04

