基于TOPSIS的装备保障网络节点重要性综合评价方法
邢 彪, 曹军海, 宋太亮, 陈守华, 董原生
(1. 装甲兵工程学院技术保障工程系, 北京 100072; 2. 中国国防科技信息中心, 北京 102205)
基于TOPSIS的装备保障网络节点重要性综合评价方法
邢 彪1, 曹军海1, 宋太亮2, 陈守华1, 董原生1
(1. 装甲兵工程学院技术保障工程系, 北京 100072; 2. 中国国防科技信息中心, 北京 102205)
针对复杂网络拓扑结构分布的不均匀性导致单一指标难以准确反映网络中节点重要程度的问题,将网络的每个节点作为1个方案,将节点重要性评价指标作为描述方案的属性,从节点度指标、介数指标、删除指标、接近中心性指标和子图指标5个方面,采用改进的逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)对网络节点的重要性进行综合评价,计算每个方案到理想方案的接近度,并按由大到小的顺序进行排序,得出节点重要性综合评价结果。最后,以某装备保障网络实例对该方法的可行性和有效性进行了验证。
复杂网络; 装备保障; 节点重要性; 多属性决策; 逼近理想解排序法(TOPSIS)
复杂网络均具有非均匀性,其核心节点的确定对于分析复杂网络的性质具有非常重要的现实意义[1]。近年来,有关寻找复杂网络中重要节点和节点重要性评价的研究,一直都是复杂网络研究的热点和难点问题之一[2-3]。
从算法上看,从复杂网络中抽取重要节点,采用定性与定量相结合的分析方法确定网络中的重要节点,实质上是对有关节点重要性评价标准和依据问题的研究。节点中心化指标[4]作为刻画节点重要程度的关键指标大致可分为2类: 1)认为节点在网络中的重要度取决于该节点与其他节点的邻近程度,如度、中心性等;2)认为节点的重要度依赖于该节点所处的位置对其他节点之间信息联络的影响程度,如介数等。此外,Everett等[5]将度、紧密度和介数3种指标推广为群组中心化指标,以适应社团的重要性评价。
在节点重要性评价方法方面,主要有基于节点删除方法[6]、基于节点之间直接连接状态[7]、网络结构和传播动力学[8]、节点收缩法[9]、信息指标[10]、PageRank算法[11]和HITS算法[12]等。以上方法均是针对不同网络的实际问题,分别从不同角度刻画节点在网络中的重要性,并提出解决方法,因此,均有其自身的优点和局限性。1)基于度的节点重要性评价方法依据节点与其相邻节点相连的边数来评价节点的重要性。但对于以下2种情况该方法并不适用:一是网络中度值相同的节点其重要度不一定相同;二是虽然网络中某一节点度值不高但是却很重要,如连接不同局域网络的唯一节点就属于这类节点。2)基于介数的节点重要性评价方法强调节点或边对网络信息的控制能力,一般采用最短路径来定义节点的重要度,但不适用于解决一些实际网络中信息不一定按照最短路径来流动的网络节点重要性评价问题。3)PageRank算法强调节点被连接的次数,尤其是被重要节点连接的次数,但无法解决存在源节点和终端节点的网络节点重要性评价问题。
针对单一指标在评价网络节点重要性中存在的局限性问题,笔者将网络中的每个节点作为1个方案,应用节点重要性评价指标来描述方案的属性,从多个角度考虑多重因素,采用相似距离改进的逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)对网络节点的重要性进行综合评价,得出更加符合客观实际的综合评价结果,并进行了实例分析及验证。
1 节点重要性指标定义与说明
基于复杂网络理论将各保障实体抽象为节点,实体间的交互关系抽象为边。
1.1 节点及边
1)定义vi为第i(i=1,2,…,N)个节点。装备保障网络中主要的保障实体有:各级作战单位相对应的保障指挥机关、各级器材仓库、各基层修理分队和运输分队等,则V={v1,v2,…,vN},为节点集合,其中N为网络节点数。
2)定义el为第l(l=1,2,…,M)条边,表示节点vi和vj的交互关系,具体为各保障实体间的传输路径和传输信息,则E={e1,e2,…,eM},为边集合,其中M为网络边数。
1.2 节点重要性指标
1)网络局部属性——度指标
度是网络拓扑结构的基本参数,可表示节点在网络中与周围邻近节点建立直接联系的能力。设ki为节点i的度,即与节点vi直接相连的节点数。若在有N个节点的网络中,ki≤N-1,则归一化的节点度指标为

(1)
从网络局部属性来看,度值越大表示节点越重要。在装备保障网络中指挥子网络是典型的垂直树状网络,军、师(旅)、团、营、连各级保障节点存在严格的指挥隶属关系,每级的保障指挥节点均需连接本级下属的所有保障子节点。因此,节点度可较好地反映装备保障网络中的保障指挥节点的重要程度,级别越高越重要,节点度值也越大。
2)网络传播属性——介数指标
介数指标侧重于度量网络中节点对信息流动的影响力。节点vi的介数为
(2)
式中:gst(vi)为节点vs和vt之间最短路径经过节点vi的条数;nst为节点vs和vt之间的最短路径条数。对于给定节点vi,若存在maxCb(vi)=(N-1)×(N-2)/2,则归一化节点介数指标为

(3)
从网络传播属性来看,若某一节点为网络中其他节点对之间通信的必经之路,则该节点在网络中十分重要。在装备保障网络中普遍存在用于连接各子网络(如维修保障子网络、供应保障子网络和保障指挥子网络等)的节点,其中以各级保障运输节点(修理连)为主,负责为各具体基层维修机构提供保障资源,是连接维修子网络与供应子网络之间通信的必经之路。有时也称这类节点为“桥”节点,适合采用介数来分析计算。
3)网络连接属性——节点删除指标
节点删除指标是通过网络的连通性来反映网络某种功能的完整性。定义节点vi删除前后,网络最大连通分支上节点数量之比作为衡量节点vi的重要度指标,即

(4)

当装备保障网络为完成规定的保障任务需要某些保障实体共同协作时,节点删除指标是从宏观角度来分析某一节点删除后对网络整体效能的影响,该类节点即使只删除1个,也会影响网络某种功能的完整性。
4)网络全局属性——接近中心性指标
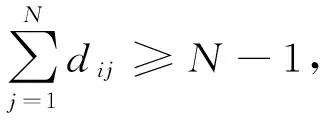
(5)
接近中心性指标可衡量装备保障网络不同地理位置上的节点重要程度,对应节点在网络中所在的位置,更能反映网络的全局结构。
5)网络耦合关系——子图指标
子图指标是对度指标的扩展,在延续度指标侧重节点直接连接关系的同时,考虑了2次(通过某一节点连接)及2次以上的连接,保证了直接连接的节点具有较大权重。具体计算方法为:计算从1个节点开始到该节点结束的闭环回路的数目,1个闭环表征网络中的1个子图。该方法可衡量节点参与不同子图的数目,并可通过对子图赋予不同的权重来表示节点间重要程度的差异。子图指标为
(6)
式中:μn(vi)为以节点vi为起点经n个连接边重新回到节点vi的闭环回路数。定义闭环回路对节点重要性的影响随长度的增加而递减。
不难看出:以上5个指标均是从某一角度来衡量节点在网络中的重要性。对于实际的装备保障网络,仅应用某一指标进行节点重要性评价其结果具有很大的局限性。
2 节点重要性综合评价与分析
TOPSIS是通过对评价对象与最优目标的接近度的排序,将最接近正理想方案同时远离负理想方案的解作为最优解。基于TOPSIS的多属性决策方法是将网络中的每个节点作为1个方案,采用多个评价指标来描述节点(方案)的属性,进而将节点重要性综合评价问题转化为多属性决策问题。
1)计算归一化决策矩阵
设A={A1,A2,…,AN},为方案集合;S={S1,S2,…,Sm},为方案属性集合,其中m为评价指标数;Ai(Sj)为第i个节点的第j(j=1,2,…,m)个指标的评价值,则决策矩阵X为
(7)
对决策矩阵X进行归一化处理,可得归一化决策矩阵T为
T=[tij]N×m,tij=Ai(Sj)/Ai(Sj)max,
(8)

2)确定理想方案
设W=[w1w2…wm],为指标权重向量,则加权规范化矩阵Y为
(9)
根据Y确定正理想方案Y+和负理想方案Y-分别为

(10)
(11)
3)计算接近度
传统方法采用欧氏距离来计算每个评价方案Ai到正理想方案Y+和负理想方案Y-的距离,即

(12)
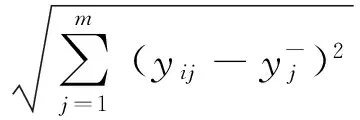
(13)
由于这种方法未考虑位于正理想方案与负理想方案垂线上的评价方案,同时为了提高评价方案的灵敏度,笔者引入相对距离对欧氏距离进行改进,即
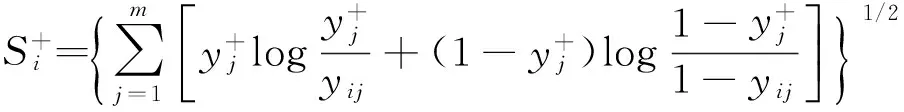
(14)
(15)
则所评价方案与理想方案的接近度Zi为
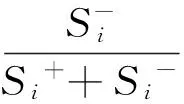
(16)

3 实例分析
以典型的基层修理分队(修理连)为例,验证笔者所提方法的可行性和有效性。图1为以修理连为中心的装备保障网络拓扑结构,其中:节点1泛指上级装备保障指挥机关(军师、旅、团等);节点2为修理营营部;节点3为修理连连部;节点4为本级所属汽车连;节点5、6分别为本级和上级装备器材仓库;节点7-10为修理连下属的4个能够完成规定保障任务的保障单元,且节点1、2分别连接2个保障单元,表示团级和营级存在可直接支配该保障单元进行机动保障的连接关系。各节点的节点度指标、介数指标、节点删除指标、接近中心性指标和子图指标的计算结果如表1所示。
由图1和表1可以看出:在该网络中,节点3的节点度和子图指标最大;节点4的介数最大;节点1-3和节点6-10具有相同的节点删除指标;节点1、2拥有最大的接近中心性指标。

图1 以修理连为中心的装备保障网络拓扑结构示例

表1 以修理连为中心的装备保障网络各节点指标的计算结果
由表1可得决策矩阵X,利用层次分析法(Analytic Hierarchy Process,AHP)确定各指标的权重。首先,依据式(17)对各指标进行两两比较,构建比较矩阵B=[bij]5×5,如表2所示,其中
bij=2, 指标i比指标j重要;1, 指标i与指标j相同;0, 指标j比指标i重要。
(17)
表2中各指标重要性比较说明:节点度指标考虑网络结构最少,且子图指标某种程度上可看作是节点度指标的扩展,因此设定节点度指标的重要性最低,子图指标的重要性最高;介数指标是唯一考虑网络信息影响的指标,适用于度量装备保障各子网络的连接关系,可发现网络中的桥节点,因此定义介数指标重要性也为最高;节点删除指标和接近中心性指标的重要程度相同,属于一般重要。
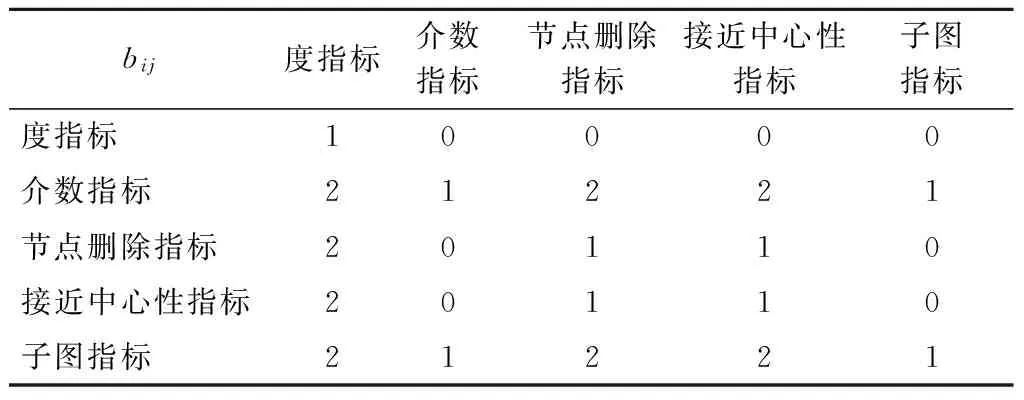
表2 指标重要性比较矩阵
其次,依据比较矩阵B构建判断矩阵,求解判断矩阵并经过一致性检验得到各指标的权重为wCD=0.057 6,wCR=wCC=0.137 9,wCB=wCS=0.333 3。由式(8)可得归一化决策矩阵T,由式(9)可得加权规范化矩阵Y为

(18)
由式(10)、(11),可得正理想方案Y+和负理想方案Y-分别为

(19)
(20)
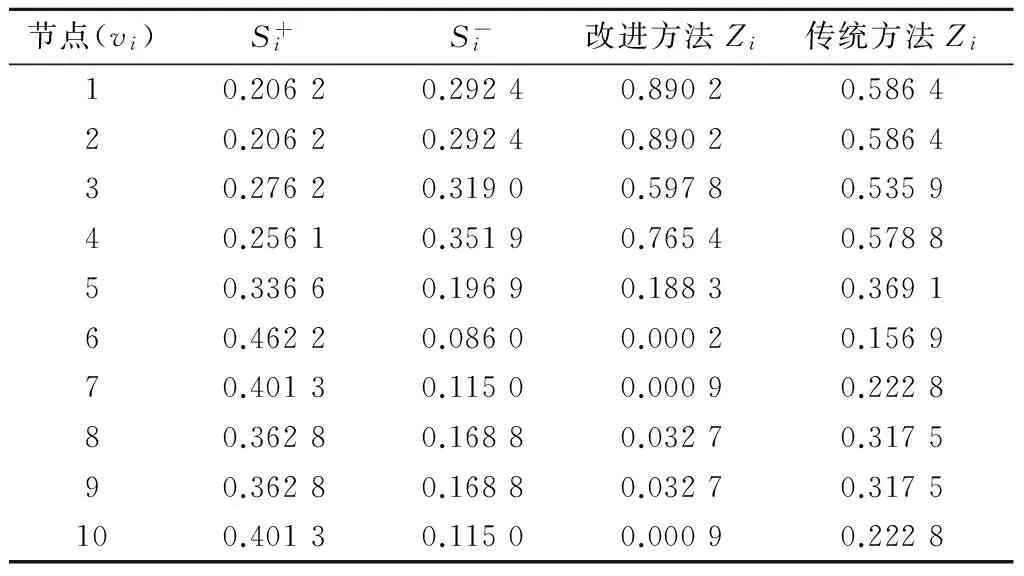
表3 以修理连为中心的装备保障网络评价结果
由表3可以看出:传统的TOPSIS法与改进TOPSIS法所得接近度Zi的排序均为
(Z1=Z2)>Z4>Z3>Z5>
(Z8=Z9)>(Z7=Z10)>Z6。
(21)
式(21)表明:1)传统TOPSIS法与改进TOPSIS法得到的节点重要性排序结果一致;2)节点1、2在以修理连为中心的装备保障网络中位置相同,具有相同的节点重要性,且节点1、2的删除会直接导致网络中通信距离的增大,故重要性最高;节点4的删除会导致修理子网络与供应子网络不再连通,故重要性次之;节点3是整个修理连的指挥中枢,具有最大的度值,但也应看到由于机动保障单元的存在,节点3的删除一定程度上可使网络通信冗余减少,团、营等上级机关直接指挥机动保障单元增大了网络的传输效率,故节点3的重要性次于节点1、2、4;节点5是介数值最大的点,删除节点5会导致上级器材仓库断开,重要性再次之;最后,剩余的其他节点的删除都不会对网络的连通性产生影响,其重要性更低。
通过以上分析可知:笔者提出的基于TOPSIS的节点重要性综合评价方法,对以修理连为中心的装备保障网络进行评价效果良好,能够较好地区分不同节点的重要程度,避免了单一评价指标的不足。为了更好地说明本文所提方法的可行性与有效性,笔者以某集团军所属的装备保障力量为研究对象,分析其与装备保障有关的各组织机构的运行过程,得出军级装备保障体系网络的运行机制和指挥流程[13],如图2所示,对其进行网络化抽象后建立军级装备保障体系结构的复杂网络模型,如图3所示。

图2 军级装备保障体系网络的运行机制和指挥流程
应用本文提出的改进TOPSIS法对军级装备保障网络中各节点的重要性进行综合评价,评价结果及排序如表4所示,并对传统TOPSIS法与改进TOPSIS法计算的节点重要性综合评价值进行了比较,结果如图4所示。
由表4可知:军级装备保障网络中排名在前10%的节点为:军级(以及下属的师旅级)装备保障指挥机关、军级(以及下属的师旅级)器材仓库、军级修理营和军级机动保障分队等,这符合装备保障的实际情况。由图4可知:传统TOPSIS法与改进TOPSIS法得到的节点重要性排序结果基本一致,但改进TOPSIS法的整体灵敏性更好,如:对于节点31-70(31-36,37-41,42-46等)的节点重要性评价,欧氏距离不能很好地进行区分,而相似距离可很容易地区分这类局部相似的节点重要性,尤其是针对装备保障网络中最底层的基本保障单元,其评价优势更为突出。

图3 军级装备保障体系结构的复杂网络模型
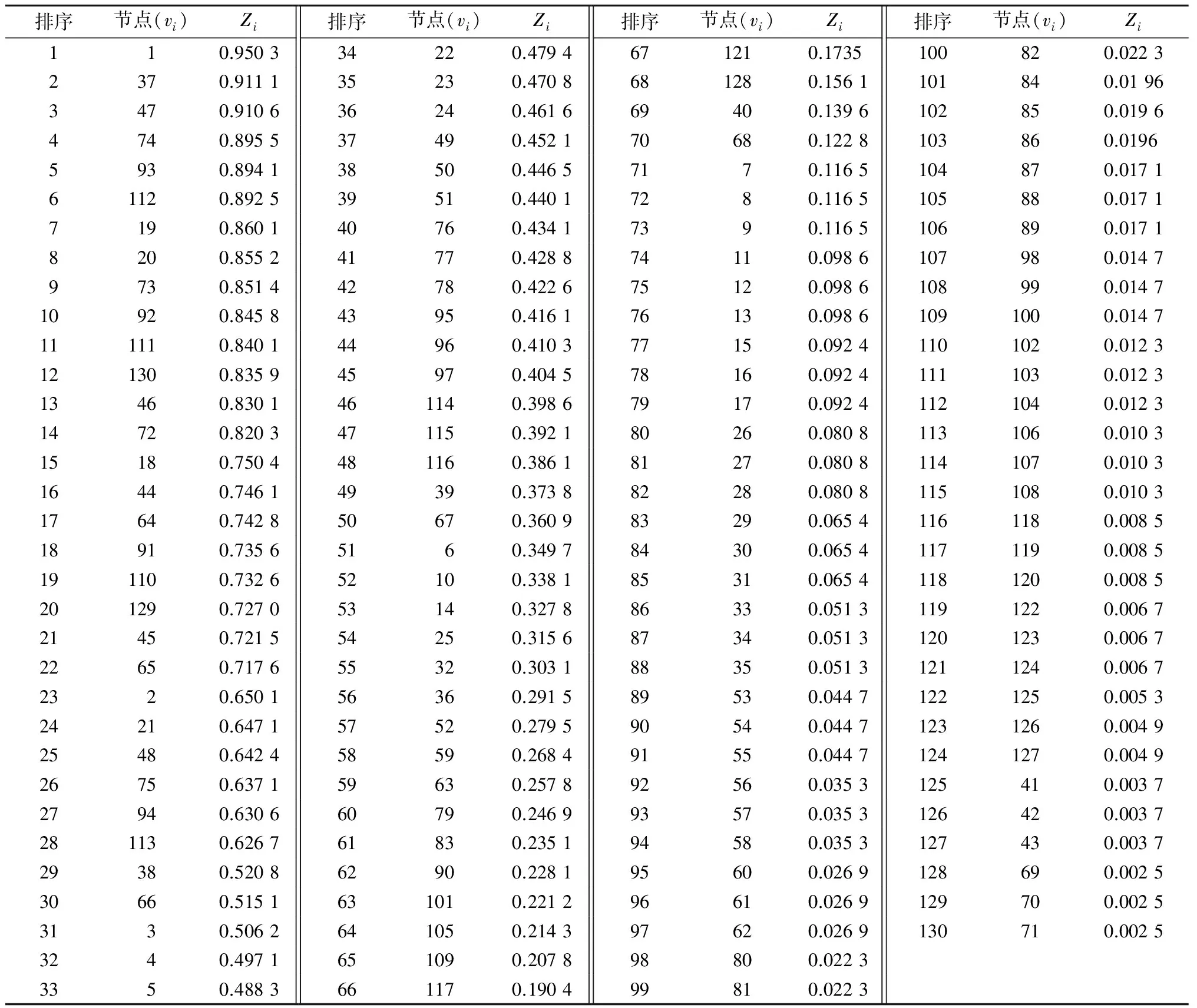
表4 基于改进TOPSIS法的军级装备保障网络节点重要性综合评价值及排序

图4 基于传统和改进TOPSIS法的军级装备保障网络中各节点重要性评价值对比
4 结论
目前,复杂网络理论已成为研究复杂系统和网络问题的有效方法,复杂网络中节点重要性的研究在实际应用中具有重要意义,但现有的评价指标如度、介数等均存在应用范围的局限性,研究网络中节点的重要性必须考虑多重因素的影响。笔者采用改进的TOPSIS方法对网络节点的重要性进行综合评价,并针对传统的欧氏距离计算方法进行了改进,该方法计算简单、易于扩展。本文的研究成果也可为进一步分析装备保障网络的可靠性和抗毁性提供决策支持。
[1] 中华人民共和国国务院新闻办公室. 2016年中国国防白皮书[R].北京:新华社,2015:2-4.
[2] ALBERT R,NAKARADO G L.Structural vulnerability of the North American power grid[J].Physical review E,2004,69(2):025103.
[3] ZHANG Y,LIU Y H.Modeling of scale-free network based on pagerank algorithm[C]∥ICFCC 2010.Wuhan,China:IEEE computer society,2010,V3:778-782.
[4] 孙玺菁,司守奎.复杂网络算法与应用[M].北京:国防工业出版社,2015:214-219.
[5] EVERETT M,BORGATTI S P.The centrality of groups and class-es[J].Journal of mathematical sociology,1999,23(1):181-201.
[6] 李旭源,罗泽,阎保平.一种基于节点删除法的候鸟栖息地重要性评估方法研究与实现[J].计算机应用研究,2015,32(2):409-412.
[7] KITSAK M,GALLOS L K,HAVLIN S,et al.Identification of influential spreaders in complex networks[J].Nat Phys,2010,6(1):888-893.
[8] POULIN R,BOILY M C,MASSE B R.Dynamical systems to define centrality in social networks[J].Social networks,2000,5(22):187-220.
[9] CHEN Y,HUA Q,HU J.A method for finding the most vital node in communication networks[J].High technology letters,2004,15(1):573-575.
[10] ZHAO P,ZHANG Y,QIAN W P.Investigation of geiger-mode detector in multi-hit model for laser ranging[J].Science China(Technological sciences),2015,58(5):943-950.
[11] PAGE L,BRIN S,MOTWANI R,et al.The Pagerank citation ranking: bringing order to the web[R/OL].(1998-01-29)[2016-10-18].http:∥ilpubs.stanford.edu: 8090/422/.
[12] 刘小弟,朱建军,张世涛,等.考虑属性权重优化的犹豫模糊多属性决策方法[J].控制与决策,2016,31(2): 297-302.
[13] 邢彪,曹军海,宋太亮,等.基于复杂网络的装备保障体系建模方法[J].装甲兵工程学院学报,2016,30(2):12-15.
(责任编辑: 王生凤)
Synthesis Evaluation Method for Network Node Importance in Equipment Support Based on TOPSIS
XING Biao1, CAO Jun-hai1, SONG Tai-liang2, CHEN Shou-hua1, DONG Yuan-sheng1
(1. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2. China National Defense Science and Technology Information Center, Beijing 102205, China)
According to the problem of the inhomogeneity of the complex network topology will lead to a failure that a single index cannot accurately reflect the degree of node importance in the network, each node in the network is taken as one program, the evaluation index of node importance are taken as the program attribute in this paper. The improved method of Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) is used to evaluate the node importance from five indicators such as node degree, betweenness, deleting index, close to center and sub-graph. The approximate degree of each scheme to the ideal scheme is calculated and sorted according to the order from large to small, and the comprehensive evaluation results of node importance are obtained. Finally, the feasibility and effectiveness of the proposed method are verified by an example of an equipment support network.
complex network; equipment support; node importance; multi-attribute decision; Technique for Order Preference by Similarity to an Ideal Solution(TOPSIS)
1672-1497(2017)03-0028-07
2017-01-10
军队科研计划项目
邢 彪(1988-),男,博士研究生。
E92; TP393.02
A
10.3969/j.issn.1672-1497.2017.03.006

