三阶非圆齿轮泵的流量脉动及可滚齿性研究

叶素娣，徐敬华

(1.芜湖职业技术学院 电气工程学院，安徽 芜湖 241000；2.浙江大学 机械工程学院，浙江 杭州 310027)

三阶非圆齿轮泵的流量脉动及可滚齿性研究

叶素娣1，徐敬华2

(1.芜湖职业技术学院 电气工程学院，安徽 芜湖 241000；2.浙江大学 机械工程学院，浙江 杭州 310027)

随着齿轮泵向高压大流量低噪声方向发展，提出了一种低困油、少脉动的非圆齿轮泵，并建立相应的节曲线模型。通过2个三阶椭圆齿轮作为工作齿轮的情形(称为3-3组合)、3个三阶椭圆齿轮作为工作齿轮的情形(称为3-3-3组合)在流量和流量脉动率方面的对比，确定3-3-3组合作为非圆齿轮泵的主要结构。非圆齿轮轮齿都有特定的啮合位置，利用坐标变换法分析了非圆齿轮的齿廓方程，为CAD建模和仿真分析提供了理论依据。用图形形式直观地反映出不同阶数非圆齿轮的凸性判别，得到三阶非圆齿轮能用滚齿法加工的条件，为非圆齿轮的加工工艺路线明确了方向。

非圆齿轮；流量脉动；齿轮泵；齿廓方程；凸性判别

高压大流量是齿轮泵发展的趋势。传统的由圆齿轮组成的齿轮泵在高压下泄漏加剧，噪声增强，效率降低[1]，因此研究少泄漏、低噪声、高效率的容积泵十分重要，非圆齿轮泵应运而生。

非圆齿轮可实现周期性变速比运动，具有独特的运动学、几何学传动特征，应用前景广阔。文献[2-6]研究了椭圆齿轮设计理论和传动性能，提出诸多齿廓优化设计方法，包括用虚拟仿真设计非圆齿轮节曲线。

1 非圆齿轮的传动比分析

图1为一对非圆齿轮相互啮合的节曲线，p为两齿轮的中心距。

设主动齿轮的阶数为n1，从动齿轮的阶数为n2，n=n1/n2，则可写出节曲线方程为：

(1)

(2)

本文中取n1=n2=3，即n=1。

r1+r2=p，由一对非圆齿轮传动的封闭性条件即纯滚动的条件，下式成立：

(3)

即中心距：

p=2a

(4)

根据齿轮传动比的定义，得到一对同阶非圆齿轮传动比的表达式：

(5)

图2为取阶数n1=1，2，3时非圆齿轮的传动比变化规律，图3为阶数n1=3时非圆齿轮副传动比随偏心率的变化规律。

由图2、图3可知，非圆齿轮的传动比随时间(主动轮转角)周期性变化，周期为T=2π/n1。图2中不同的阶数有相同的幅值，说明幅值与阶数无关；而图3中偏心率越大幅值越大，说明幅值与偏心率有密切的关系。

2 两个三阶非圆齿轮组合泵的流量脉动分析

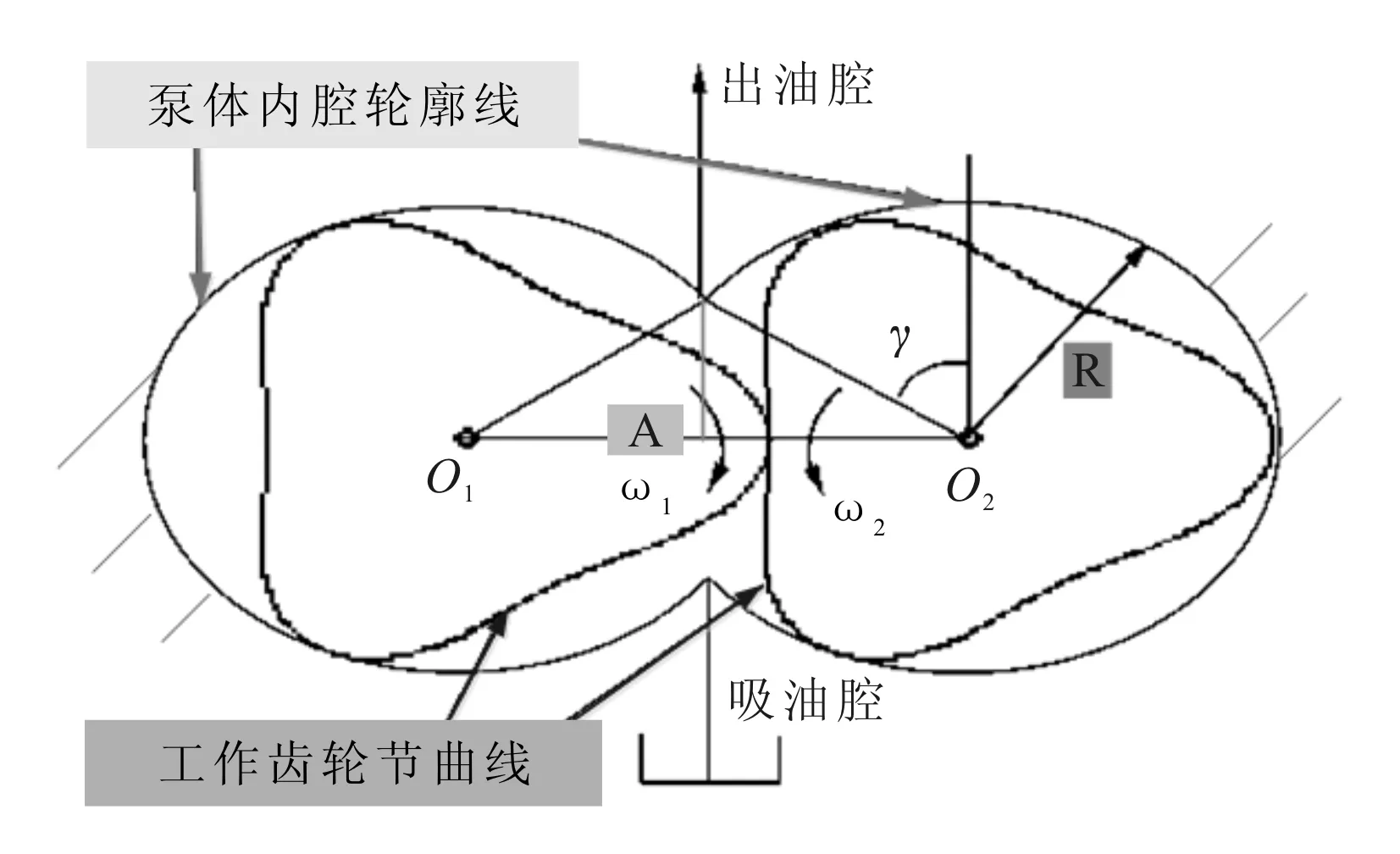
图4 3-3组合非圆齿轮泵

一对三阶非圆齿轮(简称3-3组合)的安装如图4所示，与泵体内腔轮廓线接触的是齿轮节曲线，设泵体内腔半径为R，则有R=r1max=r2max。

实际情况应是齿顶部分接触(模数较小，齿顶高ha也较小，暂时可不考虑)。

任取一微段并积分，求得三阶椭圆齿轮的面积S，具体公式如下：

(6)

设非圆齿轮泵的宽度为B，则在主动齿轮旋转一周的过程中，密封腔容积的变化(即非圆齿轮泵的排量)为：

(7)

一对非圆齿轮满足纯滚动条件：φ1r1=φ2r2，则出油腔的容积变化量为：

(8)

代入(8)，整理后得到：

(9)

(10)

式中：ω1为主动齿轮1的匀角速度。

图5所示为3-3组合在不同偏心率时，单位流量的变化规律。主动齿轮转一周，流量有三次出现极大值和极小值，这是因为三阶非圆齿轮的形状是周期性对称分布的；而偏心率越大，流量也越大，较大的偏心率意味着椭圆齿轮较扁平，封闭隔离区域的容积较大，故而流量较大。

设η为流量脉动率，则

(11)

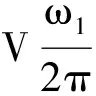
(12)

从公式(12)可知，流量脉动率与非圆齿轮的阶数无关，只是偏心率的函数。图6揭示了流量脉动率与偏心率的关系，当e=0.5时，η达到145%左右，由此在选择非圆齿轮泵时，为减小流量波动，减小压力波动，要尽量选取较小的偏心率。这与图5得出的结论——只有较大的偏心率才有较大的流量，产生了矛盾，因此3-3组合的非圆齿轮泵有待改进。

如果有一种方法能使一组齿轮的最小流量和最大流量恰巧碰上另一组齿轮的最大流量和最小流量，这样就能大大降低流量波动，而这种方法就是3-3-3组合。

3 三个三阶非圆齿轮组合泵的流量脉动分析

在图4的基础上增加一个完全相同的三阶非圆齿轮，组合成为3-3-3齿轮泵，见图7所示。

主动轮与右从动轮形成3-3组合时，下腔为吸油腔，上腔为出油腔；主动轮与左从动轮形成3-3组合时，下腔为出油腔，上腔为吸油腔。将两个吸油腔、两个出油腔分别通过管路联接，这样在主动轮整周运动过程中，封闭隔离腔的容积和较大，同时容积变化较小，亦即流量较大但波动减小，脉动率降低[7-8]。

若主动轮与右从动轮的3-3组合的啮合角为φ1，则与左从动轮的3-3组合的啮合角为π+φ1，因此新增流量为：

(13)

3-3-3组合的总流量公式为：

QZ=Q+Q′

(14)

3-3-3组合在不同偏心率e时流量的变化规律如图8所示。

3-3-3组合的流量变化周期为60°，在一个周期内最大流量和最小流量分别为：

(15)

(16)

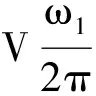
(17)

将图9与图6对比可以清楚地看出，3-3-3组合的流量脉动率远远低于3-3组合。

4 非圆齿轮齿廓设计及可滚齿性判别

(18)

以曲率半径为当量圆齿轮的节圆半径，则当量齿轮的基圆半径ρ1=ρcos20°。

(19)

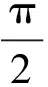
(20)

其中β=π-μ-φ1

以曲率中心M为原点，建立坐标系Mxmym，分别以ρ1和ρ为半径画基圆和节圆，并画出一段渐开线，如图11所示。

渐开线上任一点K的向径为rK，压力角为αk，展角为θk，分度圆上的展角为γ(γ=57.3°tan20°-20°) ，根据渐开线性质有：

γ=57.3°tan20°-20°

(21)

因此渐开线齿廓上一点在坐标系Oxy中的最终表达式为：

(22)

公式(22)可以形成非圆齿轮完整的齿廓。非圆齿轮的齿顶曲线和齿根曲线理论上是节曲线的法向等距线，它们与节曲线之间的法向距离分别是齿顶高ha、齿根高hf[9]。

非圆齿轮可以滚齿加工的条件是节曲线非内凹[10]，即ρ>0，将曲率半径的分母作为判别式F，则F>0。

图12为三阶非圆齿轮的凸性判别，可以看出，三阶非圆齿轮在偏心率e≤0.125时，齿轮的节曲线全部极角处F>0，能够滚齿加工。而当偏心率e>0.125，齿轮的节曲线部分极角处F<0，不能滚齿加工。

图13为不同阶数非圆齿轮的凸性判别，由图可以看出，当n=2，偏心率取至0.3时，齿轮的节曲线全部极角处F>0，能够滚齿加工；n=4，偏心率取为0.1时，已有部分极角处F<0，即不显示凸性，此时的非圆齿轮就不能通过滚制加工。

5 结语

(1) 3-3-3非圆齿轮组合相比3-3组合，具有流量大，脉动小的优点；

(2) 采用当量齿轮和坐标变换法，推导出非圆齿轮的齿廓方程，为三维建模和运动仿真提供了理论支持；

(3) 非圆齿轮的可滚齿性取决于阶数和偏心率，当n≥4时，即使e=0.1，仍会有部分极角处不显示凸性，不能用滚制方法加工成型；当n=3，偏心率≤0.125时，才能使齿轮节曲线的全部极角处都显示凸性；而当n=2时，e≥0.3还能使齿轮节曲线的全部极角处都显示凸性，能够用滚齿法加工成型。

[1] 叶素娣,徐敬华.高压大流量齿轮泵混合参数增效设计[J].机械科学与技术,2016,35(2):165-170.

[2] 张始斋,向毅,黄学满,等.非圆行星齿轮液压马达节曲线的数值计算[J].机械设计,2013,30(4):37-39.

[3] 刘永平,孟鹏飞.基于MATLAB的高阶椭圆齿轮副节曲线的设计[J].机械,2010,37(2):39-42.

[4] 黄志东,赵文珍.高阶椭圆齿轮参数化建模与模态分析[J].制造业自动化,2015,37(23):8-12.

[5] 叶素娣,徐敬华.精密变位斜齿轮行星轮系混合型变量多目标优化设计[J].机械设计,2016,33(7):98-104.

[6] 李名尧,张猛,孙健.椭圆齿轮泵流量分析[J].上海工程技术大学学报,2009,23(1)：6-8.

[7] 谭伟明.高阶椭圆齿轮多齿轮泵原理及其流量特性[J].机械传动,2012,36(8):19-22,30.

[8] 丁凡,邓民胜,刘硕,等.耐高压双向椭圆齿轮微小流量计研究[J].农业机械学报,2015,46(6):327-333.

[9] 柴树峰,张学玲,李玉兰.非圆齿轮设计及运动学仿真分析[J].军事交通学院学报,2014,16(9):36-40.

[10] 张国政,韩江,刘有余.高阶椭圆齿轮的滚齿加工方法及理论[J].计算机集成制造系统,2014,20(5):1106-1113.

[责任编辑、校对：梁春燕]

Research of Flow Pulsation & Gear Hobbing of Third-order Non-circular Gear Pumps

YESu-di1,XUJing-hua2

(1.School of Electrical Engineering, Wuhu Institute of Technology, Wuhu 241000,China; 2.School of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China)

With the development of gear pumps towards the direction of high pressure,high flow,and low noise,the paper presents a kind of non-circular gear pumps with low trapped oil and pulsation,and establishes the corresponding pitch-curve mode. By contrasting 3-3 combination with 3-3-3 combination in terms of flow and flow pulsation rate,the 3-3-3 combination is used as the main structure of non-circular gear pump.Coordinate transformation method is used to analyze the non-circular gear tooth profile equation, which provides a theoretical basis for establishing CAD modeling and simulation analysis.A graph is used to directly reflect the different order number convexity judging of non-circular gear,and obtain the conditions for the processing of three-order non-circular gears through the gear hobbing method,thus pointing out the direction for the technical route of non-circular gear processing.

non-circular gear;flow pulse;gear pump;tooth profile equation;convexity judging

2017-04-01

国家自然科学基金青年-面上连续资助项目(51005204，51375012)；浙江省自然科学基金资助项目(Y13E050014)；安徽省高校自然科研重点项目(KJ2017A553)；安徽省省级质量工程项目(2016ckjh227)

叶素娣(1969-)，女，浙江上虞人，副教授，工程师，主要从事CAD/CAE/CAM研究。

TH132.424

A

1008-9233(2017)03-0037-05