基于局部测量方法的堆石料变形特性试验研究

彭兴楠，邹德高，刘京茂,2，周晨光

(1.大连理工大学 水利工程学院， 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024)

基于局部测量方法的堆石料变形特性试验研究

彭兴楠1，邹德高1，刘京茂1,2，周晨光1

(1.大连理工大学 水利工程学院， 辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024)

在大型三轴仪中联合采用了局部轴向位移计和径向变形测量位移传感器，通过直接测量试样局部的轴向应变和径向应变，排除了端部误差的影响。在此基础上研究了堆石料小应变阶段的变形规律。试验结果表明：轴向应变在0.001%～0.01%的范围时，局部位移计测定的割线模量是外部位移传感器测量结果的1.5～2.0倍，当轴向应变达到1%时两者测定的割线模量基本一致；传统测量方法会明显高估试样的实际体应变，低估径向应变，在小应变阶段局部测量方法测定的泊松比约为传统测量方法的2.0倍。

堆石料；小应变；局部测量；径向应变；泊松比

堆石料是土石坝等土工建筑物的重要填筑材料。已有的土石坝实际工程表明，坝体大部分区域的实际应力状态均远小于堆石料的峰值应力状态，在坝体填筑和运行期堆石体一般处于小应变状态(轴向应变小于1%)，因此精确测量堆石料小应变阶段的变形特性对准确评价坝体的变形规律是非常重要的。

由于试样端部误差的存在，目前大型三轴仪传统的测量方法难以满足对堆石料小应变阶段变形特性深入研究的需求，主要体现在以下几个方面[1-3]：(1) 端部接触问题。传统三轴仪的位移传感器安装在压力室外部，测得的轴向位移中包括上下试样帽与试样之间的空隙引起的变形等端垫误差。(2) 端部约束问题。三轴试样上下端部土体受试样帽摩擦力的作用，导致试验过程中试样端部土体径向变形偏小。传统三轴仪仅能利用外部排水管测量得到试样的体积变形，然后推算出试样的径向变形，因此传统测量方法不能准确地测定试样真实的径向变形。(3) 端部“藏水区”问题。三轴试样端部存有空隙，在试样饱和后会形成“藏水区”，使传统测量方法难以准确测得试样的体积变形。许多学者提出了多种方法来排除这种端部误差。Ibraim E等[4]提出了一种在三轴仪压力室内部安装直线位移传感器LVDT测量试样局部应变的试验方法；Soga K等[5]开发了悬臂式局部位移计(Cantilever-LDT)；孔宪京等[6]在自主研制的大型三轴仪中安装了局部位移计LDT。Suwal L P等[7]在三轴仪中采用局部位移计和夹式测量计(Clip gauge)，直接测量三轴试样中部的轴向变形与径向变形；孙树国等[8]开发了激光量测系统(PSD)，可以测量试样不同位置的局部变形；邵龙潭等[9]在三轴仪中引进数字图像测量技术，可以直接测量试样不同范围内的轴向变形与径向变形。

以上研究主要是基于土工小型三轴试验，有关堆石料大型三轴试验端部问题的研究还较少，特别是在径向变形测量方面。本文在传统大型三轴仪中联合应用局部轴向变形测量装置—局部位移计和径向变形测量位移传感器，研究了堆石料小变形阶段的应力应变关系、体应变、泊松比的变化规律，得到了一些有益的成果。

1 试验测试技术

本次试验采用大连理工大学的液压伺服大型三轴仪。试样直径300 mm，高度600 mm。

1.1 轴向变形测量局部位移计LDT

由于三轴试验中的端部接触问题，传统三轴仪外部位移传感器测得的轴向位移中包含端垫误差，不能反映试样的真实变形。因此，本次试验安装了2个局部位移计[10]。试验时，局部位移计通过上下支座固定到试样中部(见图1)，测量高度500 mm，测量位置与文献[3]一致。局部位移计测定的轴向变形不仅排除了端垫误差，且试样中部的应力和变形分布比较均匀，测定的轴向变形更可靠。

图1 试样示意图

1.2 径向变形测量位移传感器LVDT

传统测量方法中，试样径向变形是通过外部体变管测定的体积变形和外部位移传感器测定的轴向变形换算得到的。由于试样端部误差的存在，传统测量方法测定的体积变形和轴向变形均不能准确地反映试样的真实变形，由此得到的径向变形也是存在问题的。

本次试验在大型三轴仪中安装了4个适用于高压水环境下的高精度位移传感器，直接测量试样中部的径向变形(见图1)，测量位置参考文献[11]。LVDT能适应恶劣的外界条件，不受外界温度和压力变化的影响。试验前分别在大气中及400 kPa、1 000 kPa、2 000 kPa水压力环境中对LVDT进行标定，标定系数均一致。由于LVDT测量位置距离试样上下端部均有一定的距离，测量的结果排除了试样端部误差的影响，测定的径向变形可信度更高。

2 试验材料

试验所用材料是某心墙坝的主堆石料，最大粒径60 mm，试验采用的颗粒级配及干密度ρd见表1。

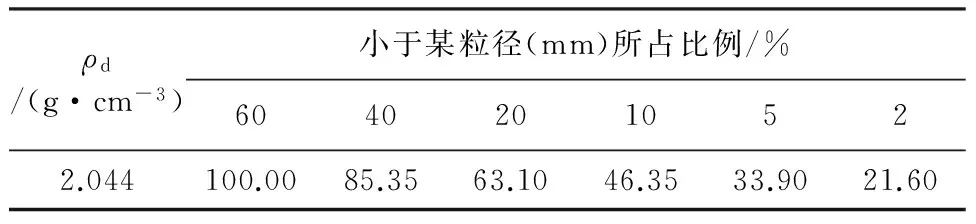
表1 密度与级配

本次试验按《土工试验规程》[12](SL239—1991)中有关标准严格地操作。试验固结围压σ3=400 kPa、700 kPa和1 000 kPa。

3 试验结果及分析

3.1 应力应变关系

图2是试验测定的偏应力q与轴向应变εa的关系，图3是割线模量Esec与轴向应变εa的关系。

图2 偏应力q与轴向应变εa的关系

图3 割线模量Esec与轴向应变εa的关系

两种方法测定的应力应变关系曲线存有很明显的差别，端垫误差对小应变阶段堆石体的割线模量的影响特别显著。外部位移传感器测定的割线模量偏低，这主要是因为外部位移传感器测定的轴向位移包含着端垫误差，高估了试样的轴向应变。而局部位移计则是直接安装在试样上，测量试验结果可信性更高。初始阶段(εa=0.001%～0.01%)局部位移计测定的割线模量是外部位移传感器测量结果的1.5～2.0倍，当轴向应变达到1%时两者基本一致。

3.2 体应变

本文列出了体应变εv三种不同计算方法的试验结果：传统测量εv=Δv/v0，整体测量方法εv=εae+2ε3，局部测量方法εv=εai+2ε3，其中Δv为试样的排水量，v0为试样体积，εae为外部位移传感器测量的轴向应变，εai为局部位移计测量的局部轴向应变，ε3为径向测量位移传感器测量的径向应变。图4(a)～图4(c)为各个围压下不同测量方法测得的体应变与轴向应变的关系。

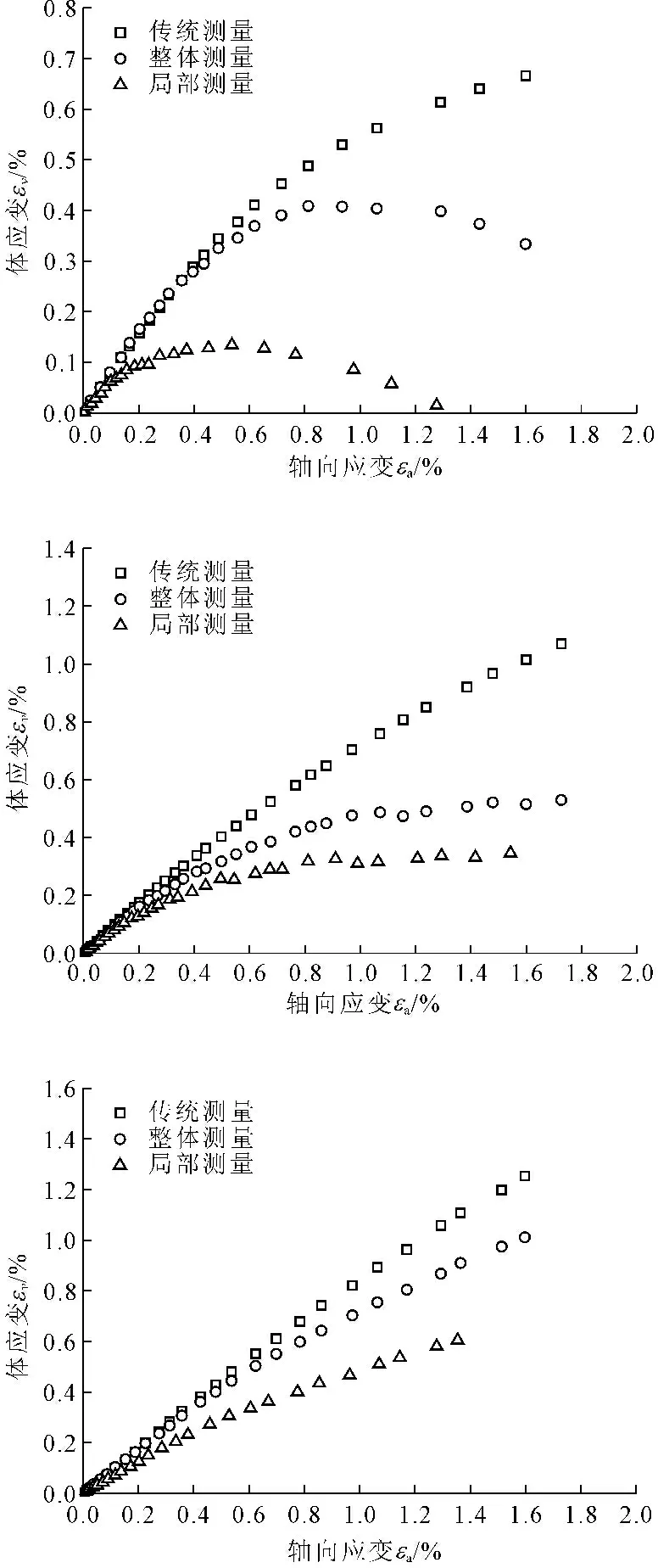
图4 体应变εv与轴向应变εa的关系

由图4(a)～图4(c)可见：(1) 初始阶段，传统测量和整体测量方法测定的体应变结果较一致，但随着变形的增大，两者差别增大，传统测量方法测定的体应变偏大。这可能是因为随变形增大，端部约束作用的影响逐渐显著，试样径向开始出现“鼓状”不均匀变形，试样端部径向变形偏小，导致传统测量方法测得的径向应变比径向测量位移传感器测得的结果偏小，体应变偏大；(2) 整体测量方法较局部测量方法测定的体应变大。因为外部位移传感器测定的轴向变形中包含着端垫误差，从而导致整体测量方法结果中的轴向应变偏大。

综上，传统测量方法高估了试样的体应变，低估了试样的径向应变。局部测量方法直接测量试样中部的轴向应变与径向应变，均排除了试样端部误差的影响，能够更准确地反映试样的实际变形。局部测量方法对试样的剪胀特性更敏感。

3.3 泊松比

目前国内外土石坝静力分析过程中广泛使用的是邓肯-张本构模型[13-14]。泊松比是邓肯-张本构模型中重要的变形参数之一，对大坝有限元计算中坝体的水平位移及应力状态具有重要的影响[15]。土体与其他固体材料性质有很大的区别，土体所受荷载较大时会出现剪胀现象，泊松比将会大于0.5[16]。

切线泊松比μt=-∂ε3/∂εa，传统测量方法中径向应变ε3需要通过ε3=(εv-εa)/2计算得出。但是由于试样端部误差的影响，传统测量方法测定的外部轴向应变和体应变均含有误差，测定的泊松比是不准确的。

图5是局部测量方法和传统测量方法得到的径向应变-ε3与轴向应变εa的关系。可见传统测量方法测定的径向应变(绝对值)小于局部测量方法的结果，低估了试样的径向应变。

图5 径向应变-ε3与轴向应变εa的关系

图6是局部测量方法和传统测量方法得到的切线泊松比μt与轴向应变εa的关系。由图6可知：(1)小应变阶段局部测量方法测定的泊松比约是传统测量方法的2.0倍，且局部测量方法测定的泊松比增长较快；(2) 不同围压下局部测量方法测定的泊松比均从0.1～0.2范围开始变化，并且泊松比在加载初期随轴向应变变化迅速，之后变化较缓慢；(3) 相同轴向应变条件下，泊松比随围压增大会减小。这与砂土现有的研究成果是一样的，随围压增大试样会更加密实，径向变形能力减弱。

图6 泊松比μt与轴向应变εa的关系

4 结 论

(1) 两种测量方法测得的应力应变关系曲线存有很明显的差别，对小应变阶段堆石体割线模量的影响特别显著。初始阶段(εa=0.001%～0.01%)局部位移计测量的割线模量是外部位移传感器结果的1.5～2.0倍，当轴向应变达到1%时两者基本一致。

(2) 传统测量方法高估了试样的体应变，低估了试样的径向应变和剪胀性。局部测量方法直接测量试样中部的轴向应变与径向应变，均排除了试样端部误差的影响，能够更准确地测量试样的径向应变与体应变。局部测量方法对试样的剪胀特性更敏感。

(3) 不同围压下局部测量方法测定的切线泊松比均从0.1～0.2范围开始变化，并且泊松比在加载初期随轴向应变变化迅速，之后变化较缓慢。相同轴向应变条件下，泊松比随围压的增大会减小。小应变阶段局部测量方法测定的泊松比约是传统测量方法结果的2.0倍。

[1] 王助贫,邵龙潭.三轴试验土样的端部影响问题研究[J].岩土力学,2003,24(3):363-368.

[2] 董建军,邵龙潭.考虑端部效应影响的非饱和压实土三轴试验研究[J].岩石力学与工程学报,2010,29(9):1937-1944.

[3] 孔宪京,贾革续,邹德高,等.微小应变下堆石料的变形特性[J].岩土工程学报,2001,23(1):32-37.

[4] Ibraim E, Di Benedetto H. New local system of measurement of axial strains for triaxial apparatus using LVDT[J]. ASTM Geotechnical Testing Journal, 2005,28(5):436-444.

[5] Yimsiri S, Soga K, Chandler S. Cantilever-type local deformation transducer for local axial strain measurement in triaxial test[J]. Geotechnical Testing Journal, 2005,28(5):445-451.

[6] 孔宪京，韩国城，娄树莲，等.高精度大型液压伺服静动三轴仪研制报告[R].大连：大连理工大学海岸与近海工程国家重点实验室,1997.

[7] Suwal L P, Kuwano R. Statically and dynamically measured poisson's ratio of granular soils on triaxial laboratory specimens[J]. Geotechnical Testing Journal, 2013,36(4):493-505.

[8] 孙树国,陈正汉,冷 文,等.基于高精度PSD的三轴试样径向变形激光量测系统的研制[J].岩土工程学报,2007,29(10):1587-1590.

[9] 邵龙潭,孙益振,王助贫,等.数字图像测量技术在土工三轴试验中的应用研究[J].岩土力学,2006,27(1):29-34.

[10] Goto S, Tatsuoka F, Shibuya S, et al. A simple gauge for local small strain measurements in the laboratory[J]. Soils & Foundations，1991,31(1):169-180.

[11] Hoque E, Tatsuoka F. Triaxial testing system for measuring loading-rate effects during cyclic tests of sand[J]. Geotechnical Testing Journal, 2004,27(5):483-495.

[12] 中华人民共和国水利部.土工试验规程:SL237—1999[S].北京:中国水利水电出版社,1999.

[13] 李云清,邹德高,董博文.心墙掺砾黏土料静力本构模型的对比分析[J].水利与建筑工程学报,2015,13(5):208-211.

[14] 邓同春,岑威钧,董坤明,等.Duncan模型若干修正适用性研究[J].水利与建筑工程学报,2013,11(3):141-144.

[15] 邹越强,季益洪,赵正军.泊松比对土石坝应力水平的影响[J].合肥工业大学学报(自然科学版),1995,18(4):63-69.

[16] 孙益振,邵龙潭,范志强,等.非黏性土泊松比试验研究[J].岩土力学,2009,30(S1):63-68.

Experimental Study on Deformation Characteristics of Rockfill with Local Measurement Method

PENG Xingnan1, ZOU Degao1, LIU Jingmao1,2, ZHOU Chenguang1

(1.SchoolofHydraulicEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China;2.StateKeyLaboratoryofIndustrialEquipmentStructuralAnalysis,DalianUniversityofTechnology,Dalian,Liaoning116024,China)

It is very important to evaluate the deformation law of the dam by accurately measuring the deformation characteristics in the small strain stage. Because of the existence of end errors, the traditional large triaxial apparatus can not accurately measure the deformation characteristics of rockfill in the small strain stage. So local axial displacement transducer and radial displacement transducer are used in the large triaxial apparatus, measuring the local axial strain and radial strain directly, and the effects of the end errors are eliminated. By using this technique we study the deformation characteristics of rockfill in the small strain stage. The results show that the secant modulus measured by local axial displacement transducer is 1.5 to 2.0 times of the results measured by external displacement transducer when axial strain is between 0.001% and 0.01%. When the axial strain comes to 1%, the results achieved by two different means become consistent basically. Traditional measuring method overestimate the volumetric strain and underestimate the radial strain. The poisson's ratio measured by local deformation is about 2.0 times of the result measured by traditional means in the small strain range.

rockfill; small strain; local measurement; radial strain; poisson's ratio

10.3969/j.issn.1672-1144.2017.03.022

2017-02-07

2017-03-10

国家自然科学基金项目(51678113)；水利部土石坝破坏机理与防控技术重点实验室开放研究基金项目(YK916005)

彭兴楠(1990—)，男，河南新乡人，硕士研究生，研究方向为筑坝堆石料小应变变形特性试验研究。 E-mail:pxndl156@163.com

TU521

A

1672—1144(2017)03—0110—05