一类二阶三点边值问题的正解

张永军

（合肥学院 学报编辑部，安徽 合肥 230601）

[数学与统计]

一类二阶三点边值问题的正解

张永军

（合肥学院 学报编辑部，安徽 合肥 230601）

利用锥上拉伸与压缩不动点定理，研究了一类二阶三点非线性边值问题以及该系统正解的存在性，得到了存在正解的几个充分条件。

不动点定理；三点边值问题；锥

0 引 言

微分方程中一个重要研究方向，即常微分方程的边值问题，目前，数学和物理学中的许多研究成果已经出现了许多二阶非线性微分方程的多点边值问题。因此，近年来二阶三点边值问题成为许多学者与专家研究的热点，且得到了许多有意义的 结 果 ， 可 参 阅 文 献[1-8]。 文 献[7]利 用 锥 上 的 不 动 点定理，在满足次线性或超线性条件下，讨论了如下系统

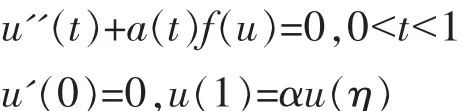
的 正 解 性 质 。 文 献[8]针 对 一 类 二 阶 非 线 性 常 微 分 方程三点边值问题。

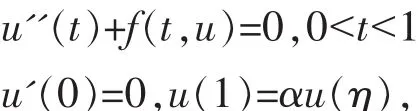
给 出 了 该 系 统 平 凡 解 的 存 在 性 结 论 ， 受 文 献[7-8]的启发，本文研究了如下一类非线性二阶三点边值问题的正解的存在性，其中 f∶[0.1]×[0，+∞）→R 连续，0＜ η＜1，α＞0 均为常数。 最终给出系统（1）（2）正解存在性的充分条件。

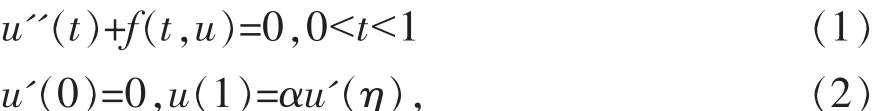
1 预备知识

首先给出几个引理。

引理 1[7]：设，α≠1 则对 σ∈C[0，1]，边值问 题有唯一解

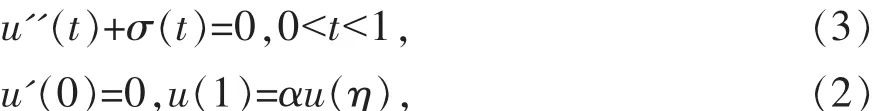
唯一解满足：

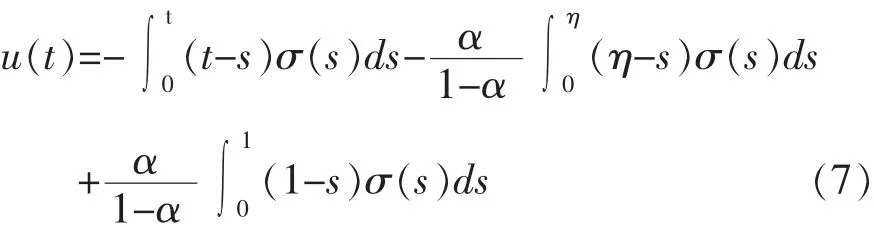
引 理 2[7]： 设 ，α≠1， 则 对 σ∈C[0，1]，σ≥0 则 边值问题（3）（2）的

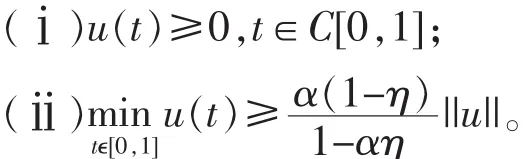
为了讨论边值问题（1）（2）的正解的存在性，我们主要利用下面的范数形式的锥拉伸与锥压缩不动点定理。

引 理 3[9]：设 E 是一个 Banach 空间 ，K 是 E 中 的一个锥，Ω1，Ω2是 E 中的有界开集，0∈⊂Ω2，又 A∶K∩→K 是一个全连续算子。 如果满足条件

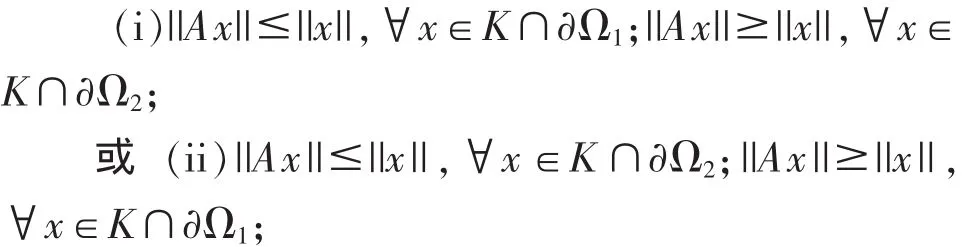
2 主要结果

记 E=C[0，1]，则 E 是 一 个 Banach 空 间 ，定 义其范数为，则 K 是 E 中的一个锥。

定义算子 A∶E→E 如下：

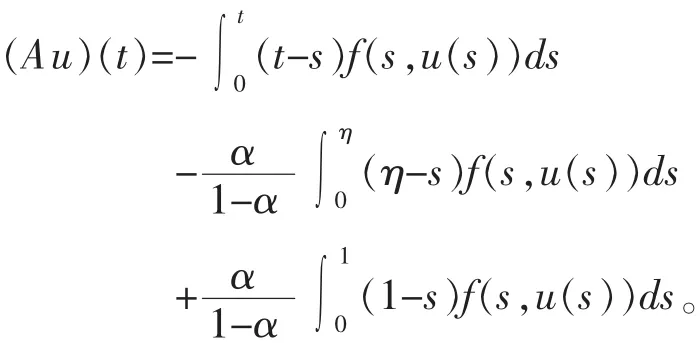
由引理 1 知，若算子 A 在 E 中存在不动点，则边值问题（1）（2）在 E 中必存在正解。

定理 1： 假设 f （t，u）∶[0，1]×[0，+∞]→[0，+∞]连续。若条件成立 ，则 边值 问 题（1）（2）在 E 中 至 少 存 在 一 个正解。

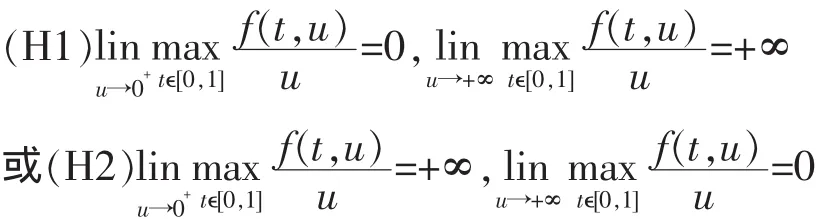
证明：由引理 2，AK⊂K，由算子 A 的定义 g（t，u） 的连续性不难证明算子 A是E中的一个全连续算子。

假设条件（H1）成立，故可选取 ε1＞0，使得 ε1＜2（1-α），则 由等式知，存在 r1＞0 使得对任意的 0≤u≤r1≤有 f（t，u）≤ε1u

记 Ω1={u∈E∶||u||＜r1}，则对∀u∈K∩∂Ω1，有 0≤u（t）≤||u||=r1，从而

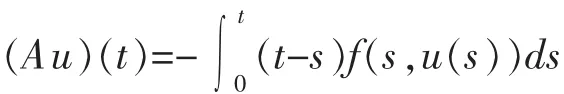
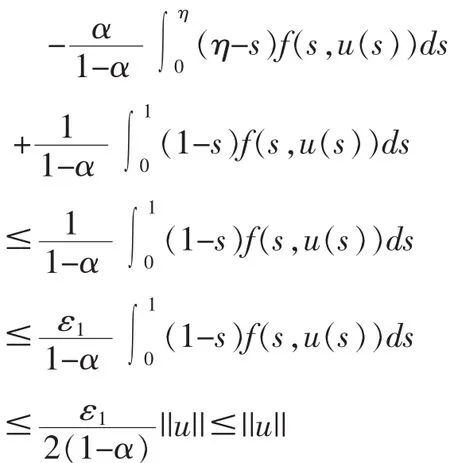
从而，当 u∈K∩∂Ω1时有||Au||≤||u||

另一方面，选取 ρ1＞0，使得，则由等式知，存在 R1＞0（R1＞r1），使得对任意的 u≥R1有 f（t，u）≥ρ1u

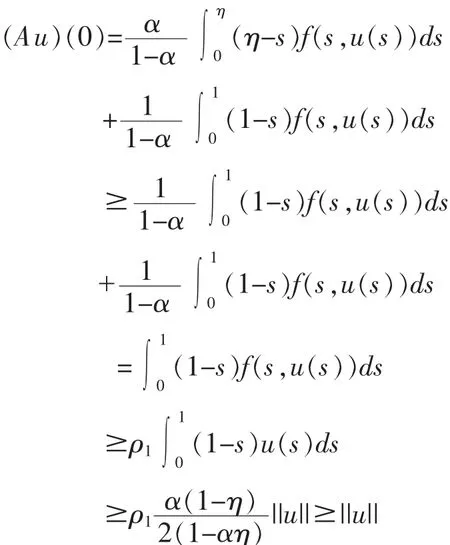
于是，当 u∈K∩∂Ω2时有||Au||≥||u||。 故由引理3 知， 算子 A 存在一个不动点 u0∈K∩（Ω2Ω1），也即边值问题（1）（2）至少存在一个正解。

假设条件（H2）成立。

首 先 ， 选 取 ρ2＞0， 使 得，则由知，存在 r3＞0，使得 当 0＜u＜r3时 f（t，u）≥ρ2u。

记 Ω3={x∈E ∶||x||＜r3）， 则 当 u ∈K ∩∂Ω3时 有0≤u（t）≤||u||=r3，t∈[0，1]，从而有

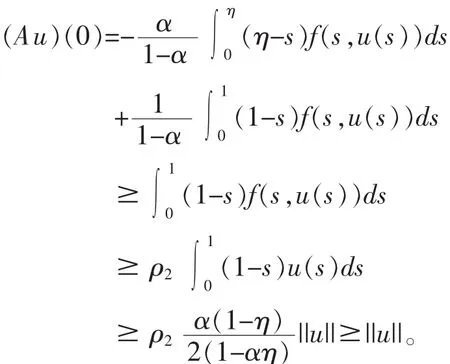
另一方面，选取 ε2＞0，使得则由等知 ， 存 在 R2＞0（R2＞r3） 使 得 对 任意的 u＞R2有 f（t，u）≤ε2u。

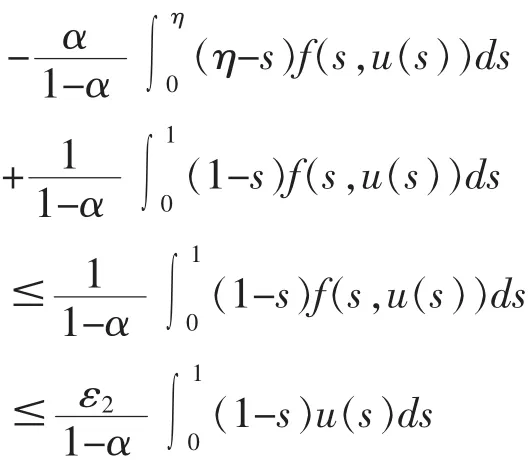
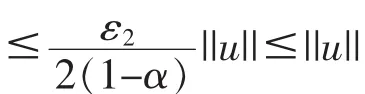
故由引理 3 知，算子 A 存在一个不动点 u0∈K∩，也即边值问题（1）（2）至少存在一个正解。

[1]Li Ren-gui,Liu Li-shan.Positive solutions of Boundary Value Problems for Second-order Singular Nonlinear Differential Equations[J].Applied Mathematics and Mechanics，2001，22(4):495-500.

[2]杨 海 艳 ，陈 海 波.二 阶 三 点 边 值 问 题 正 解 的 存 在 性[J].数 学理论与应用，2008，28（3）：97-102.

[3]Liu J，Feng H Y.Positive solutions for a second-order threepoint boundary value problem[J].Journal of Natural Science of Heilongjiang Universsity June，2015，32(3):325-329.

[4]李淑红.二阶三 点边值问题 正解的存在 性[J].高校应用数学学报，2007，22（4）：441-446.

[5]马巧珍.非线性 三点边值问 题正解的存 在 性[J].应用泛函分析学报，2001，3（2）：178-182.

[6]许也平，李淑 红.一类次 线 性三点边 值 问题正解 的 存在性[J].丽水学院学报，2006，28（5）：1-4.

[7]马巧珍.非线性 三点边值问 题正解的存 在 性[J].应用泛函分析学报，2001，3(2):178-182.

[8]李淑红.一类二 阶非线性方 程三点边值 问 题 解 的 存 在 性[J].丽水学院学报，2005，27（2）：1-3.

[9]郭 大 均.非 线 性 泛 函 分 析[M].济 南 ：山 东 科 学 技 术 出 版 社 ，2001.

责任编辑：胡德明

A Study on a Kind of Second-order Three-point Boundary Value Problem's Positive Solutions

Zhang Yongjun
(Editorial Department of School Journal,Hefei University,Hefei 230601,China)

By utilizing a fixed point theorem on a cone in Banach space,the existence of positive solutions for a kind of nonlinear second-order three-point boundary value problem is studied in this paper, and obtained some sufficient conditions for the existence of positive solufive solutions.

fixed point theorem;three-point boundary value problem;cone

O175

：A

：1672-447X（2017）03-0001-03

2017-04-21

张永军（1975-），安徽合肥人，合肥学院学报编辑部副编审。