轻型直升机的飞行动力学特性分析

姜波

中国电子科技集团公司第二十七研究所，河南 郑州 450047

直升机飞行动力学是为直升机总体设计服务、建立直升机飞行动力学非线性数学模型的一项全局性工作，涉及的学科众多，如空气动力学、旋翼空气动力学、自动控制理论、计算数学等[1]。直升机飞行动力学非线性数学模型是开展操稳特性分析、飞行实时数值/半实物仿真、飞行控制系统设计等研究的基础。它经历了从线性模型向非线性模型、从简单模型向复杂模型（包含飞行控制、发动机动力学及控制增稳等子系统）发展的过程，研究的飞行状态也由定常飞行向机动飞行发展。

为了满足高性能武装直升机发展的需求，国内外对直升机飞行动力学建模做了较系统的理论研究。针对不同的机型，发展了多种直升机飞行动力学非线性数学模型及其改进型，如直升机飞行动力学ARMCOP模型[2]、AH-64A直升机飞行动力学模型[3]、UH-1H直升机飞行动力学模型[4]、UH-60A直升机飞行动力学模型（GENHEL）[5]等。在进行理论模型研究的同时，还进行了大量的风洞和飞行试验，以验证所建数学模型的精确度和可靠性。不少模型在工程实际中获得了很好的应用。

1 直升机飞行力学模型

本文针对常规单旋翼带尾桨直升机建立其数值仿真模型，该模型是多体动力学系统，包含旋翼、尾桨、机身等各部件的气动力模型、运动学模型及模型间的耦合与约束。本文采用层次化、模块化的建模思路，部件为独立的仿真实体，仿真实体间的数据接口为力、力矩、姿态和机体轴速度等。这种模块化的思路保证了仿真系统的灵活性。相关轻型直升机的详细数据根据参考文献[6]和参考文献[7]整理。

直升机模型由机身动力学、旋翼系统、发动机和控制增稳系统子模型构成。机身动力学模型：机身气动模型在大角度范围内定义了非线性的机身升力、阻力和侧向力[X，Y，Z]f，wt及俯仰、滚转及偏航的各向力矩 [L，M，N]h，其影响参数为机身迎角αf，、侧滑角βf、旋翼下洗流系数emr和机身动压。机身的力与力矩在风轴系中计算后以Ch/wt矩阵转化到体轴系。旋翼模型：主旋翼与尾桨采用非线性模型定义拉力 T、阻力 H 和侧向力 J、铰接式桨毂力矩 [L，M，N]hub，h，并且从悬停状态至后飞、侧飞等情况均适用。旋翼模型包含变化的入流比λ、桨叶惯性矩Ib、桨叶扭转θ1、旋翼锥度a0、旋翼挥舞铰偏置量e和尾桨挥舞调节系数δ3等参数。旋翼的力在控制轴系中计算以矩阵Ch/s转化到体轴系。控制系统模型：直升机控制系统模型将飞行员的驾驶杆操纵、总距控制和脚蹬控制转化为主桨与尾桨的总距与周期变距操纵A1afs和B1afs。自动飞行控制系统主要提供直升机的滚转、俯仰和偏航的速率稳定性。

风场扰动与飞行员的操纵输入一起作为直升机模型的输入，分解为平均风速和湍流（旧称紊流）分量，采用Simulink的德莱顿（Dryden）形式湍流模型。

2 模型的构建

2.1 坐标系

体轴系的运动方程使用所有的力[X，Y，Z]与力矩[L，M，N]，计算机体的线加速和角加速度。线加速度积分后得出机体的运动速度[u，v，w]as，h并转化到地轴系，再次积分后得到直升机的位置[x，y，z]cg，e。角加速度积分后得到机身的角速度 [p，q，r]h，转化到欧拉角 [Φ，θ，φ]h并积分得到直升机的姿态。

2.2 机身动力学模型

机身动力学的数据在Simulink中以查表模块（Lookup Table）差值的形式组成。风轴系的力和力矩主要受迎角αf、平尾的当地来流角ito和侧滑角βf，机身角速度和动压影响。机身空气动力模型在大的迎角和侧滑角（±10º）范围定义非线性的三向力和力矩，数值与旋翼下洗emr、机身角速率和动压相关。机身采用ICEM软件划分非结构四面体网格，流场区域（前6L后10L，上下左右各6L），最大面网格32，最小网格8，网格数量570万， CFX计算流体软件计算力与力矩[8]，如图2所示。对流项采用二阶迎风格式离散，湍流模型为SST k-ω，迭代次数200，平均残差控制1E-5。机身横向气动力特性如图2所示。

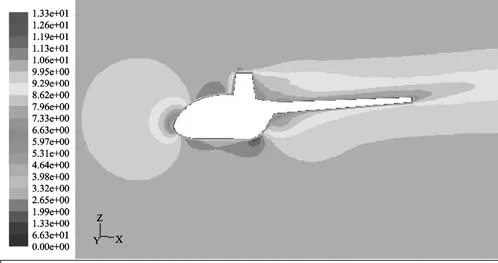
图1 机身迎角3°的速度分布Fig.1 Velocity contours for the fuselage 3 degree angle of attack

机身气动力矩从风轴系转换到体轴系，力矩包括CFX软件坐标系原点计算力矩，由于原点与重心偏移的附加力矩，角速度和旋翼下洗对尾部的阻尼。机身在体轴系的力矩为：

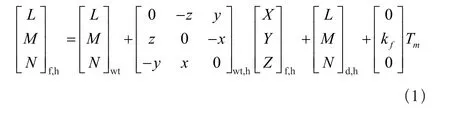
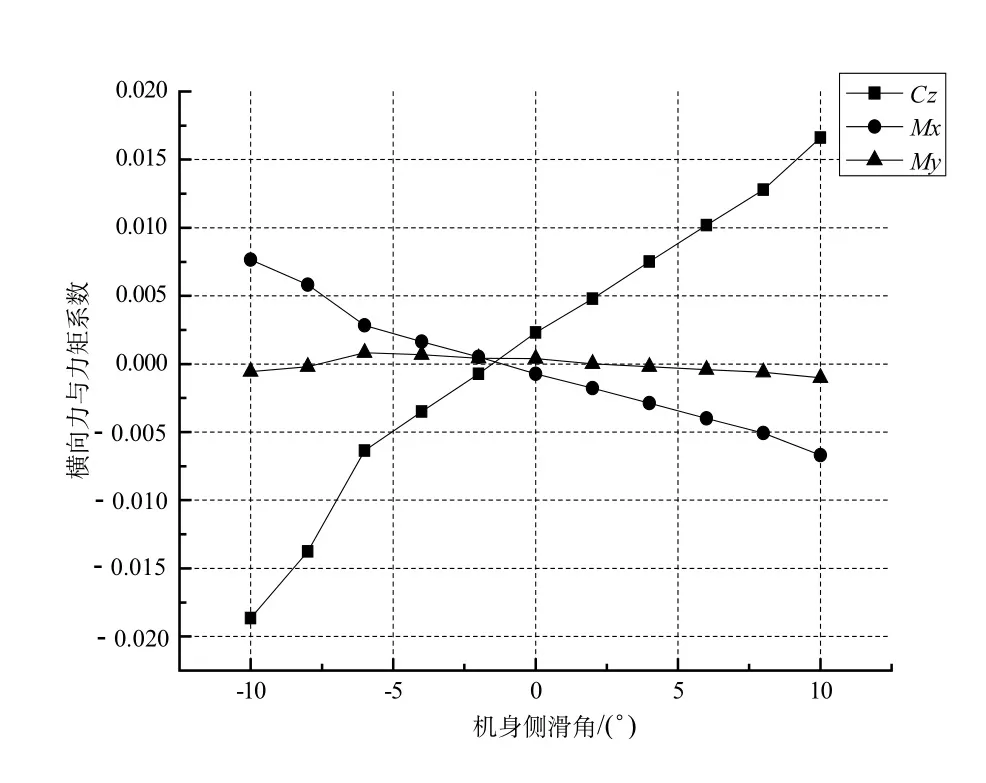
图2 机身横向气动力特性Fig.2 Lateral aerodynamic characteristics of the fuselage

2.3 旋翼模型

旋翼的力和力矩使用非线性经典旋翼理论，参考文献[4]的假设条件，这种简单的旋翼模型在实时仿真中相对易用，主要假设条件包括：旋翼桨盘采用均匀入流；忽略旋翼桨叶的摆振运动、压缩和失速的影响；只考虑旋翼桨叶的一阶谐波运动。

旋翼桨毂在控制轴系中的速度计算：空速最开始在主轴坐标系中确定，使用直升机空速[u，v，w]as，h和角速度[p，q，r]h转换到控制轴系。

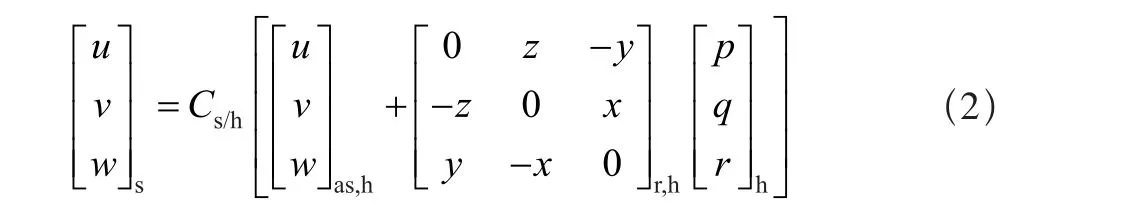
在尾桨模型中，由于没有周期变距，对应的B′1和A′1项为0。桨尖速度和诱导速度比直接影响到旋翼的力和力矩，其为控制轴系的桨毂速度函数。诱导速度比v通过对定常状态的诱导速度滤波得到，时间常数τv考虑了旋翼入流改变的延迟，拉力系数CT和入流λ都是v的函数，所以为一阶非线性微分方程。其微分方程为：

控制轴系中的旋翼拉力T和锥度角a0是旋翼速度比值的三次函数：

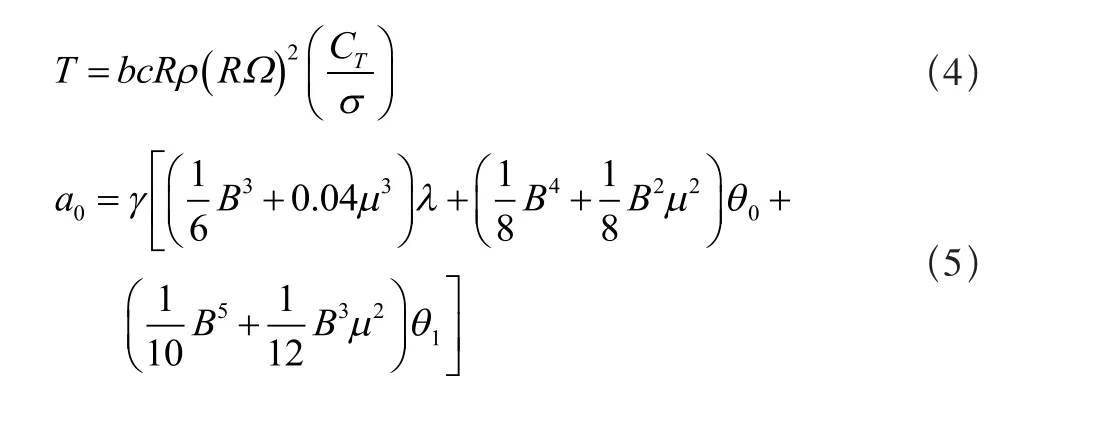
式中：θ0是桨根处的桨距角，θ1是桨叶扭转度数。在拉力系数CT/σ方程中涉及到的桨叶质量惯性矩项在α0的表达式中被忽略。

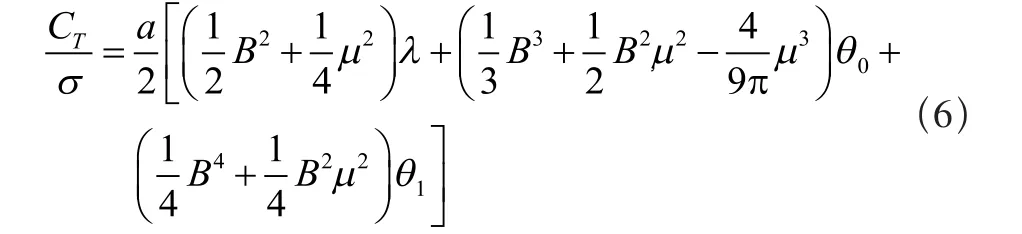
旋翼挥舞角，其计算要求先得控制轴系中的到机身角速度[p，q，r]c，旋翼挥舞角α1和b1用以下方程在控制轴系中计算：

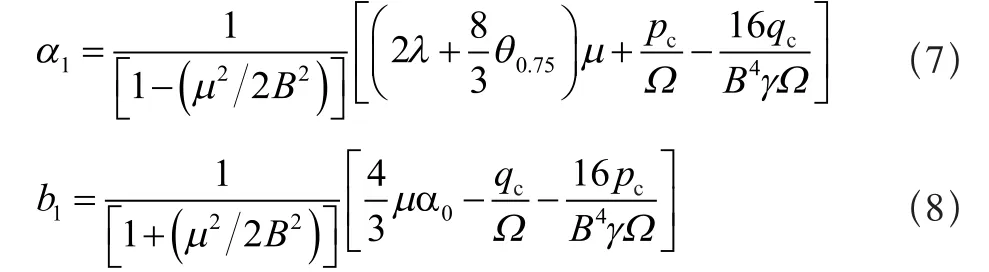
对于线性扭转和弦长不变的桨叶，其总距角可用3/4展向位置的桨距角θ0.75代替。旋翼后向力：

小角度α′是旋翼拉力和诱导速度的函数，其表达式与纵向挥舞角α1相似：

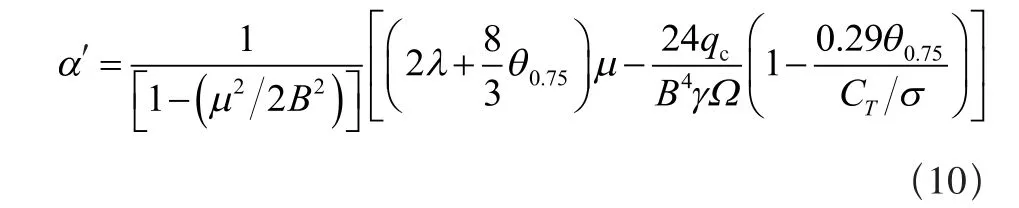
侧向力的计算公式：

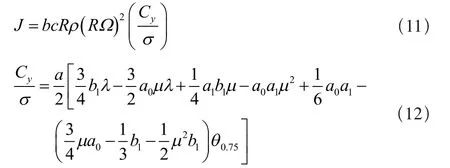
将旋翼力从控制轴系转换到体坐标系方程如下：

将桨毂轴系中的旋翼力矩转换到机体轴系中，旋翼作用于机身的总力矩包含：桨毂力矩（由于挥舞角偏置形成）和桨毂相对重心偏移导致的额外力矩。

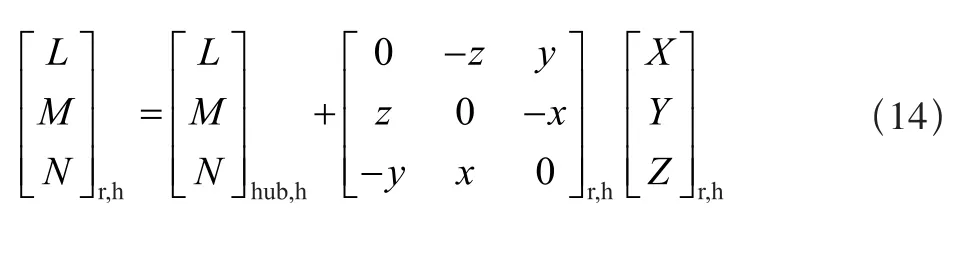
以上模型表示了直升机主旋翼的模型。而尾旋翼具有δ3铰，旋翼锥度和挥舞运动均影响桨叶变距；模型作以下修正：

其中：θct是控制系统指定的总距值。锥度角α0（见式（12））是θ0的函数，因此对于尾旋翼模型，式（5）和式（15）同时求解。

2.4 发动机和控制器模型

发动机和控制器模型包括了旋翼气动扭矩和作用于机身之间延迟。验证模型时取自参考文献[5]的涡轮轴发动机模型。模型包括压气机涡轮作用、动力涡轮作用、叶片惯性矩和轴间干扰，涉及到参考转速Ω0和主旋翼气动扭矩CQ，以计算主旋翼、尾桨和发动机的扭矩数值。

2.5 控制系统模型

控制系统模型包含操纵输入、控制交叉耦合、自动飞行控制系统和伺服作动器。定义了主旋翼总距θom、纵、横向周期变距B1和A1、尾桨总距操纵θct。模型取自参考文献[5]。

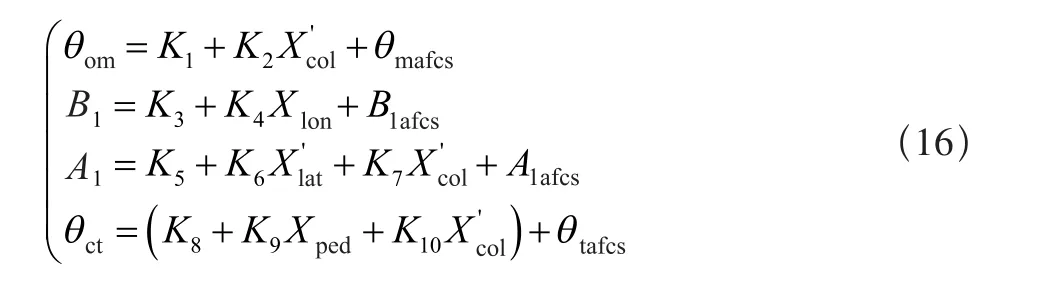
对于小的操纵位移，应避免响应过于灵敏，其中总距操纵量X′col>2.54cm时：

总距操纵量被限定在-0.0349rad（-2.0º）到0.419rad（+24.0º）范围内。上式中飞行员的输入是相对位置的控制量。当系统仿真进入航向保持、定高等增稳模式时，控制系统模型根据配平角Φtrim和Ψtrim分别表示输出相应的A1afs、B1afs操纵量[3]。

2.6 运动方程模型

直升机的运动方程定义在体轴系，以假定平整不旋转的大地为参考系。直升机假定为刚体且相对Xh-Zh平面质量对称，忽略发动机角动量的影响。

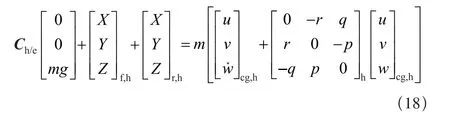
运动方程的转换（加速度等式）如下：式中：Ch/e为地轴系到体轴系的转换矩阵，Φh、θh和Ψh是相对机体坐标系定义的欧拉角，式（18）可作以下变换：

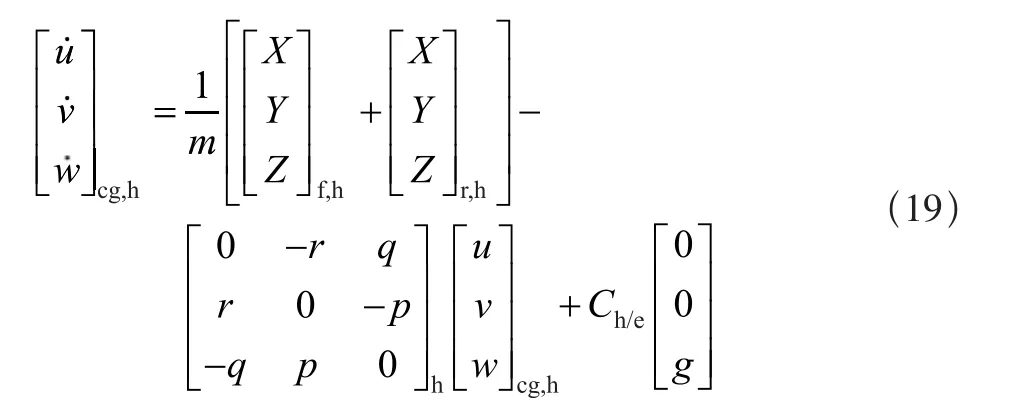
体坐标系中的惯性速度通过对式（19）的时间积分和初始条件设定得到，体坐标系中的直升机位置通过对速度表达式的积分得到。旋转运动方程（角加速度形式）为：

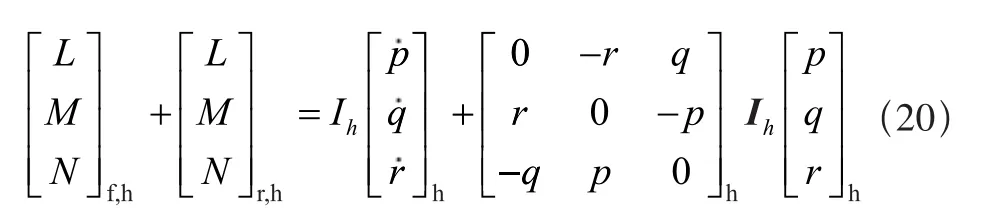
其中：Ih为直升机的惯性矩阵，式（20）等式可变换为：

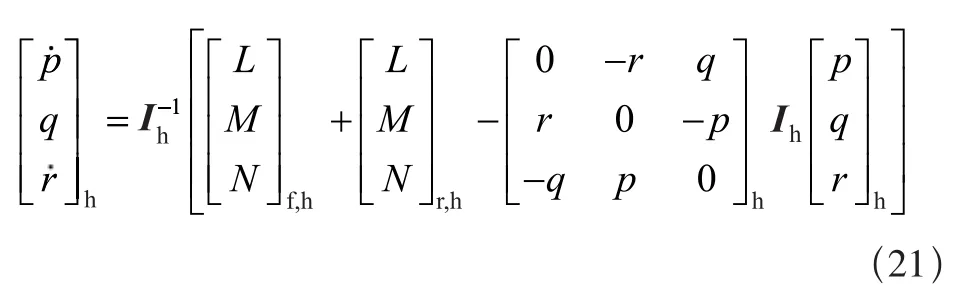
机体坐标系中角速度通过对式（21）的时间积分和适当的初始条件得到，直升机的欧拉角通过以下积分公式：

2.7 时域内的模型验证

为验证基于Simulink模型方法的正确性，选择NASA报告[9]的试验数据进行对照，为与结果对比，按试验模型参数设定初始参数，包括主旋翼转速Ω=185r/min，全机总质量m=18614kg等，对比结果如图3所示。

对于纵向周期变距的脉冲输入响应对比，实线代表文献的试验数据，虚线代表模型的仿真值。欧拉角和机体轴系中的角速度吻合良好。此处假设横向配平功能未启用，因轴间耦合因素，横向滚转角在脉冲操作后未归零。合理的修正包含将阻尼增益等增稳参数做出调整和对不同机身构型的气动特性调节。

2.8 某轻型直升机分析实例

利用前面介绍过的理论方法和模型搭建过程，在可快速设定直升机的不同起飞重量、高度和飞行速度的条件，首先对某轻型直升机的原型机无侧滑时前极限重心、正常重心、后极限重心三种状态进行了配平计算，如图4所示。

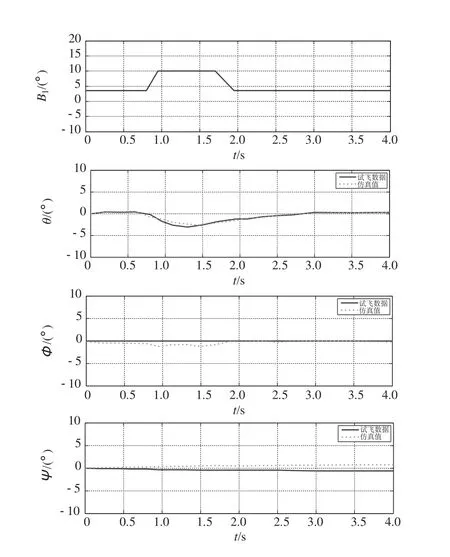
图3 试飞与数学模型对比Fig.3 Flight test and math model comparisons

动态响应数值模拟也称为操纵性计算。利用该数学模型，采用四阶方法提供候选解，五阶方法控制误差的Runge-Kutta算法（ODE45数值方法）求解，对原型机进行了动态响应仿真计算。分析时关闭增稳控制系统的作用，只根据直升机对某一操纵输入的主要响应曲线来判断计算结果的合理性，如图5所示。

3 结论

通过建立基于Simulink的轻型直升机的简化飞行动力学模型，并验证了模型的可信度。对某轻型直升机的无人化改装研究提供了理论依据，以此为基础得到以下结论：

（1）该机型符合常规单旋翼有人驾驶轻型直升机的配平特性：在正常重心的定常飞行状态，机身的姿态角接近水平状态，有利于减少机身阻力和保证乘员的舒适性，并且尾桨距等操纵量均有较大的机动余量（θOTR=-10.6º～+19.5º）；机体的重心布置前后不同时，对纵向周期变距操纵的影响较大，而其他操纵通道关联弱，在改装为电传伺服舵机的行程方面需着重考虑。

（2）操纵响应方面，经模型仿真计算显示：前推杆之后（△B1=1°），直升机产生低头、向前加速的运动；纵向速度u随时间而递增即前飞速度加快，俯仰角θ负方向增加即直升机低头程度增大，对应的俯仰角速度q也呈现负值。基本能够反映在某一操纵输入后，直升机初始时刻的运动或运动趋势，计算结果是合理的。

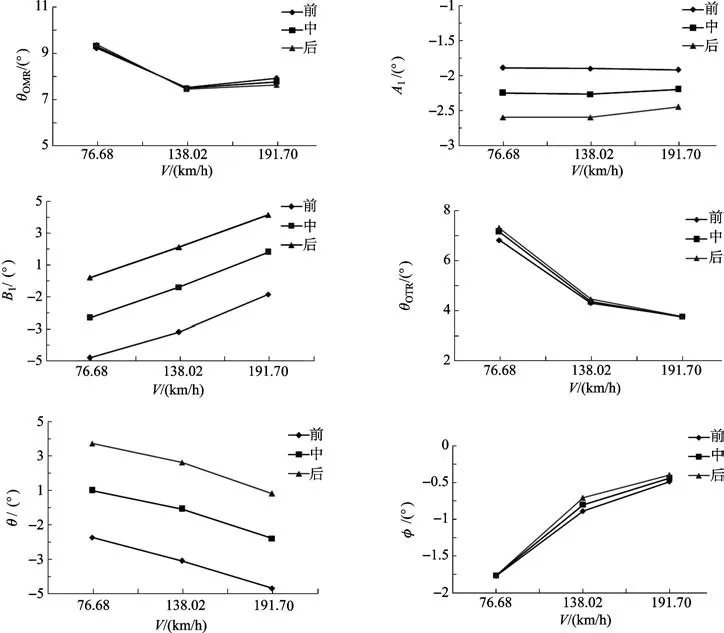
图4 操纵量及姿态角随速度的变化（G=620kg，H=0，β=0，不同重心位置）Fig.4 The control value and attitude angle with the speed（G=620kg，H=0，β=0，Different center of gravity）

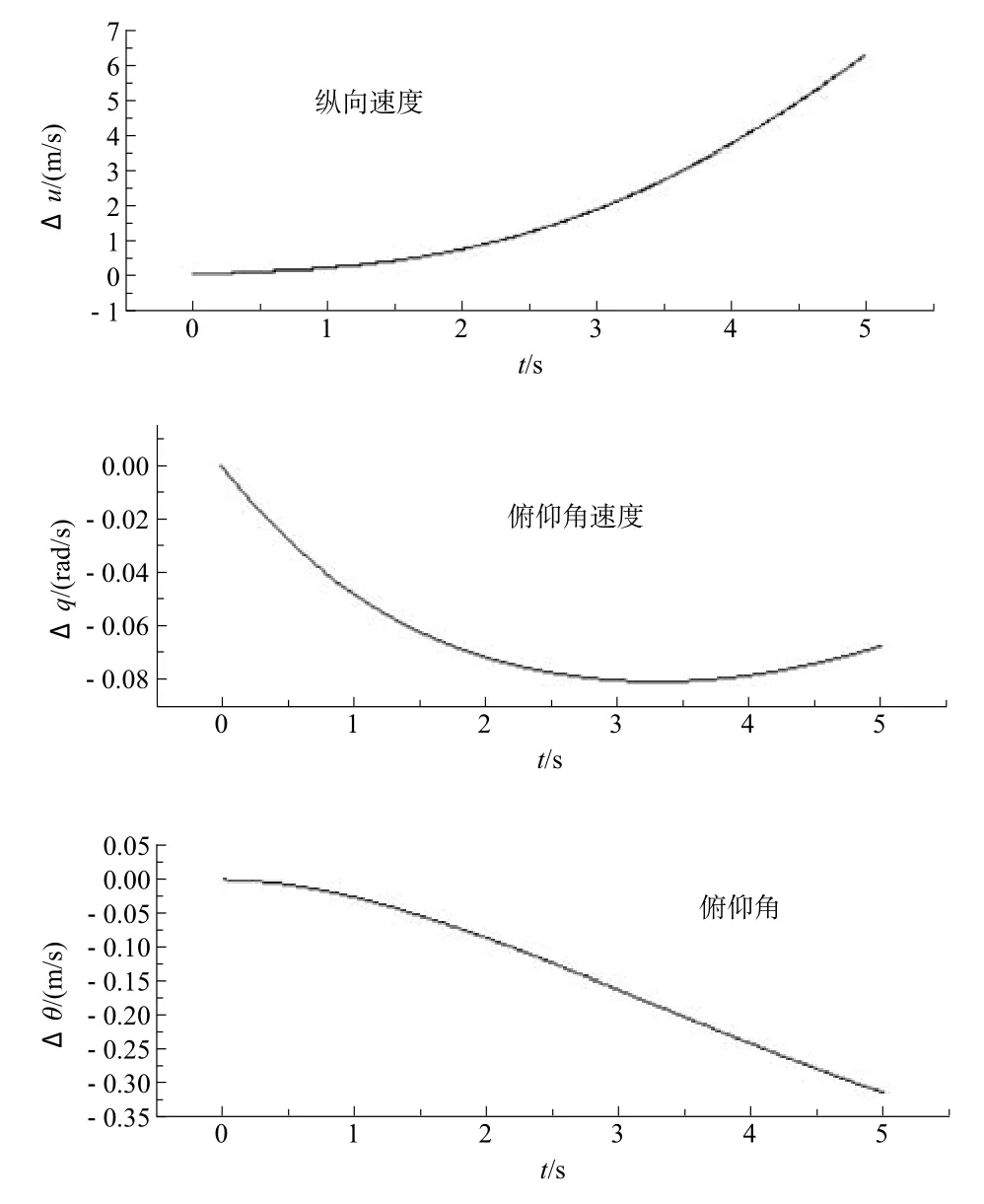
图 5 动态响应（μ=0.25，△B1=1°，阶跃输入）Fig.5 Dynamic response（μ=0.25， △B1=1°，β=0，Step input）

[1] 高正，陈仁良.直升机飞行力学[M].北京：科学出版社，2003.GAO Zheng， CHEN Renliang. Helicopter fl ight dynamics [M].Beijing：Science Press， 2003. （in Chinese）

[2] Shaughnessy J D， Deaux T N， Yenni K R. Development and validation of a piloted simulation of a helicopter [R] . NASA，1979.

[3] Aiken E W. A mathematical representation of an advanced helicopter for piloted simulator investigations of control-system and display variations [R]. NASA， 1980.

[4] Talbot P D， Corliss L D. A mathematical force and moment model of a UH-1H helicopter for fl ight dynamics simulations [R].NASA， 1977.

[5] Howlett J J. UH-60A black hawk engineering simulation program[R]. NASA， 1981.

[6] Robinson model R22 maintenance manual [Z]. U. S.： Robinson，2004.

[7] 普劳蒂R. W.. 直升机性能及稳定性和操纵性 [M]. 北京：航空工业出版社， 1990.Prouty R W. Helicopter performance， stability and control [M].Beijing： Aviation Industry Press，1990. （in Chinese）

[8] 王福军. 计算流体动力学分析：CFD软件原理与应用 [M]. 北京：清华大学出版社， 2004.WANG Fujun. Computational fluid dynamics analysis： CFD software principles and applications [M]. Beijing： Tsinghua University Press， 2004. （in Chinese）

[9] Sturgeon W R. A mathematical model of the CH-53 helicopter[R]. NASA， 1981.