导电圆环电感系数的计算方法辨析

龙中权， 周东明， 尹家贤

(1.北京宇航系统工程研究所， 北京 100076 2.国防科学技术大学 电子科学与工程学院， 湖南 长沙 410000)

导电圆环电感系数的计算方法辨析

龙中权1， 周东明2， 尹家贤2

(1.北京宇航系统工程研究所， 北京 100076 2.国防科学技术大学 电子科学与工程学院， 湖南 长沙 410000)

本文计算了导电圆环的内自感系数和外电感系数。对于通有低频电流的导电圆环，可近似认为电流在导电圆环的截面内均匀分布，且导电圆环半径远大于导电圆环截面半径。导电圆环的内自感系数可以根据直导线的内自感近似得出；而外电感系数可以根据导电圆环的空间辐射场计算得到。结果表明，最终得到的电感系数与实际工程经验相符。文中采用的方法为任意几何形状导电环的外电感系数的计算提供了有效参考。

导电圆环；内自感；外电感

0 引言

导体回路的交变电流所产生的交变磁场在自身回路中会产生感应电动势，这属于电感现象，可以用电感来描述。

导线中的电流，在导线内部、外部都会产生磁场。因此，对于一般导线而言，不仅存在外电感，同时也存在内电感。

长直导线或长直螺线管的电感都不难求出，而导电圆环的结构并不复杂，其电感的计算却并非容易。

本文首先讨论了将导电圆环等效为磁振子，根据磁振子的辐射场，由电感的定义计算出导电圆环的外电感。经验证，这种思路存在一定的问题，本文对此进行了详细的讨论。计算导电圆环电感的方法是将导电圆环分割成无数短直导电圆柱，计算出各短直导电圆柱在空间的辐射场；导电圆环的辐射场可以看成是各个导电圆柱辐射场的叠加，进而根据电感的定义计算出导电圆环的外电感。而导电圆环内电感可以根据直导线的内电感近似得到。

1 导电圆环内电感系数的计算

本文主要讨论导电圆环在通有低频电流情况下其电感的计算，所以，电流I可以近似认为在导电圆环的截面内均匀分布。

假设导电圆环的截面半径为a，圆环半径为R。将导电圆环放置于直角坐标系的XY平面内，如图1所示。

图1 导电圆环放置示意图

由于在导电圆环的内部存在电磁场，则存在内磁通，所以存在内电感Li。因为电流在圆环截面均匀分布，所以当圆环的半径远大于圆环的截面半径时(R>>a)，导电圆环的内电感可以足够近似地按照长直导线内电感情况计算。

一段长为l，导电材料的磁导率为μ的长直导线内电感为[1]

(1)

从而，圆环半径为R的导电圆环的内电感为

(2)

2 导电圆环外电感系数的计算

导电圆环的外电感系数比较难以计算。目前，工程上普遍使用导电圆环的外电感计算公式为[2]

(3)

式(3)成立的前提条件是：假设电流在导电圆环的截面内均匀分布，且R>>a，即：导电圆环的半径远大于导电圆环的截面半径。考虑到，在满足上述条件的情况下，导电圆环的内电感往往可以忽略。

本文首先讨论将导电圆环等效为磁振子来计算其外电感；然后讨论将导电圆环分割成无数短直导电圆柱，通过计算其辐射场来计算外电感。

2.1 等效磁振子方法中存在的问题

由电磁场基本理论可知，小导电圆环在空间的辐射场可以等效为磁偶极子在空间的辐射场。所以，可以尝试将导电圆环等效为磁振子，通过计算磁振子的辐射场，再来计算导电圆环所包围平面的磁通量，然后根据电感的定义计算出导电圆环的外电感。

1) 导电圆环的空间辐射电磁场

已知磁振子在空间产生的电磁场为[3]

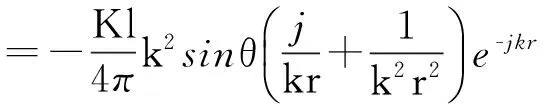
(4)

(5)

(6)

其中K为自由空间波阻抗，l为磁振子的长度，k为波数。

根据两者之间的对应关系，可以得到导电圆环的空间辐射电磁场：

(7)

(8)

(9)

其中，R为导电圆环的半径

2) 计算导电圆环外电感

由于考虑的是低频电流下的导电圆环电感系数，所以导电圆环几何大小相对其产生的电磁场的波长来说属于电小尺寸。

考虑导电圆环的近场，忽略低阶项，得到

(10)

(11)

由回路的电感的定义可知

(12)

将式(10)与式(11)代入式(12)，在导电圆环所包围的面上进行积分，得到电流环的电感：

(13)

对式(13)进行积分，得到导电圆环的电感

(14)

(15)

考虑到R≫a，式(13)可近似为

(16)

上述计算导电圆环外电感的思路是将导电圆环等效为磁振子，通过计算磁振子在空间的辐射场，从而得到导电圆环在空间的辐射特性。然后由式(13)计算出导电圆环的外电感。

根据式(16)可以发现，由上述思路最终得到导电圆环的外电感与导电圆环的截面半径没有关系，只与导电圆环的半径成正比，这显然不符合实际的工程经验，也与公式(3)相矛盾。

出现上述错误推论的原因是导电圆环辐射场的计算存在问题。问题出在哪里？简单地认为导电圆环的辐射场可以直接等效为磁振子的辐射场，这种等效是有一定前提条件的。一般情况下，小电流环辐射场与磁基本振子辐射场的等效关系，只有在小电流环中通有高频电流情况下，两者的辐射场才近似相同。并且，如果将导电圆环等效为磁偶极子，算出其辐射场后，不能再返回去计算磁偶极子围绕区域的场分布。

问题就出在将通有低频电流的导电圆环的辐射场等效为磁振子的辐射场是不正确的。

2.2 等效导电圆柱方法

低频情况下，电流I在导电圆环的截面上近似均匀分布。 并且，满足条件R≫a，所以，在计算过程中，可以将导电圆环截面的电流看成在圆环截面中心线集中分布。

将导电圆环分割成无数段弧长为dl的导电圆柱，由于细分的导电圆柱弧长长度很小，故可以将其近似看成是短直线导电圆柱。所以，导电圆环在空间的辐射场可以等效为各无限小导电圆柱辐射场的叠加。

在导电圆环上与 轴的夹角为β处，取出一段弧长为dl的导电圆柱进行研究(如图1所示)。将短直导电圆柱放置于X1Y1Z1坐标系内，方向朝Z1轴放置，如图2所示。

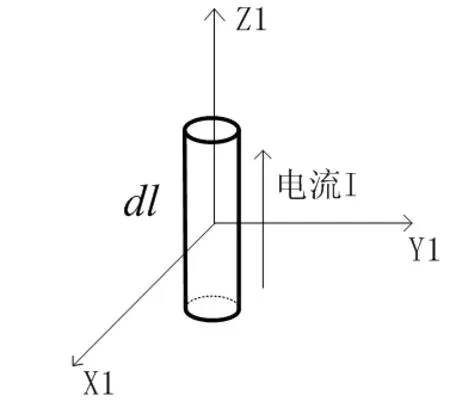
图2 长度为dl的导体柱放置示意图

1) 无限小短直导电圆柱辐射场的计算

在通有电流I的导电圆柱中，截面电流密度

(17)

由矢量位公式

(18)

计算得到圆柱的矢量位

(19)

以上计算得到导电圆柱的矢量位是在直角坐标X1Y1Z1下计算的结果，为了方便后续的计算，需要将AZ1转化为基于X1Y1Z1直角坐标的球坐标下进行研究，即：

(20)

(21)

根据矢量位与磁场强度的关系

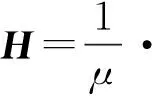
(22)

得到短直导电圆柱在空间产生的辐射电磁场为

(23)

(24)

(25)

由于考虑的是低频电流，在所考虑圆环半径范围内的辐射场是导电圆柱辐射的近场。

经过上述简化，长度为dl的短直导电圆柱的空间辐射场为

(26)

2) 坐标系的转换

上述的结果是在坐标系X1Y1Z1下得到的辐射场，X1Y1Z1坐标系是动坐标系，随着角度β的变化而变化。为了使参考坐标系一致，有必要进行坐标变换，将X1Y1Z1坐标系下导电圆柱的辐射场转换到XYZ坐标系下进行研究。

XYZ坐标系与X1Y1Z1坐标系的空间位置关系如图3所示，X1轴与X轴的夹角为β。

图3 两个坐标轴之间的几何关系

由坐标系的转换关系可得到两坐标的坐标转换矩阵

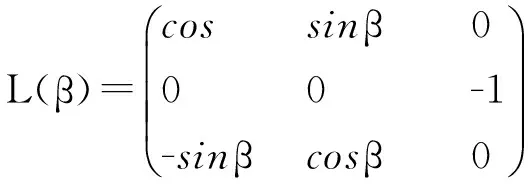
(27)

从而X1Y1Z1坐标系与XYZ坐标系之间的转换关系为

(28)

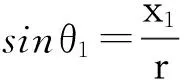
按照式(28)的转换关系，式(26)转换到XYZ坐标系后，得到

(29)

将式(29)转化为极坐标并化简

(30)

3) 导电圆环外电感系数的计算

对式(30)在圆环所包围的面内进行积分：

(31)

由式(31)可得到导电圆环在空间辐射的近磁场。从而，当圆环内的电流为I时，圆环包围的半径为(R-a)圆面内的磁通Φ为

(32)

所以，导电圆环的外电感

(33)

给定导电圆环的截面半径a以及导电圆环的半径R，根据式(33)，通过数值积分即可算出各种情况下导电圆环的外电感。

综合上述分析，导电圆环的电感由内电感Li和外电感Le两部分组成。导电圆环的总电感为内电感Li和外电感Le之和，即

L=Li+Le

(34)

实际上，导电圆环的内电感相对于外电感可以忽略。

4) 结果讨论

对式(33)进行数值积分，绘制导电圆环的外电感随导电圆环半径与截面半径比值(R/a)变化的曲线；同时对经验公式(3)取相应点的数值以做比较，得到的图形如图4所示。

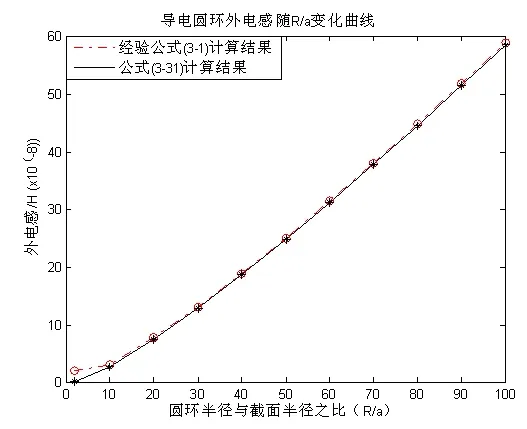
(a) R/a值较小

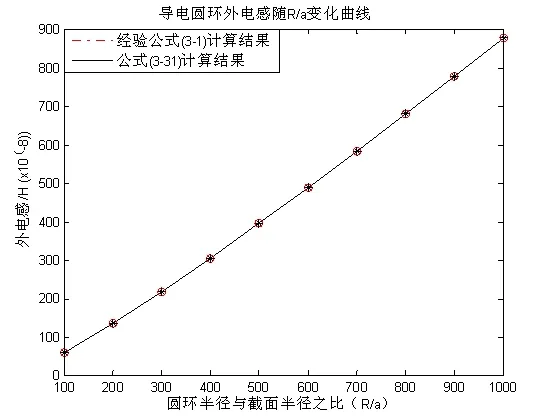
(b) R/a值较大时图4 导电圆环外电感随R/a变化曲线

对比图4可以发现，当(R/a)较小时，式(33)计算出的电感与工程经验公式(3)计算出的结果差别较大，如图4(a)中的第一个点(R/a=2),两者的差别比较明显；当(R/a)较大时，两个公式的计算结果

符合非常好。并且，随着导电圆环半径与圆环截面半径的比值(R/a)增大，两个计算公式的误差逐渐减小。当R/a=50时，两个公式的误差低至1%，上述误差完全在可接受范围内。

3 结语

本文针对导电圆环的电感进行了研究，包括导电圆环的内电感和外电感，导电环的总电感如式(34)所示。

导电圆环的内电感可以根据直导线内电感近似得出。对于外电感，本文首先讨论了将导电圆环等效为磁振子，再进行相关的计算。分析表明，这种思路存在一定的问题，为此给出了合理的解释。

本文采用的方法是将导电圆环分割成无数个短直导电圆柱，通过计算各个导电圆柱的辐射场，然后对所有导电圆柱的辐射场叠加，得到导电圆环的辐射场。根据电感的定义，计算出导电环的外电感。计算结果如式(33)，这与工程经验公式(3)符合非常好。

本文采用的等效导电圆柱计算电感的方法，为计算任何几何形状导电环的外电感提供了一定的参考。

[1] 路宏敏，赵永久，朱满座. 电磁场与电磁波基础(第二版)[M]. 北京：科学出版社，2012

[2] 钟顺时. 电磁场基础[M]. 北京：清华大学出版社，2006

[3] 魏文元，宫德明等. 天线原理[M]. 北京：国防工业出版社，1985

Analysis of Calculating Inductance Coefficient of Conducting Circular Ring

LONG Zhong-quan1， ZHOU Dong-ming2， YIN Jia-xian2

(1BeijingInstituteofAerospaceEngineeringSystem,Beijing100076，China2CollegeofElectronicScienceandEngineering，NationalUniversityofDefenseTechnology,Changsha410000，China)

This paper explores the inductance coefficient of conducting circular ring, including internal self-inductance coefficient and external inductance coefficient. With consideration of low frequency current in conducting circular ring, the current can be regarded as distributing uniformly in cross section of the ring. The internal self-inductance can be calculated according to the inductance of straight line conduct; and external inductance can be calculated by the electromagnetic radiation field of conducting circular ring. The results show that the inductance coefficient conforms very well to engineering experiences. Furthermore, the methods adopted in this paper can be a reference calculating the inductance coefficient of conducting ring of any shape.

conducting circular ring; internal self-inductance; external inductance

2016-05-21;

2016-09-09

龙中权(1991-)，男，在读研究生，研究方法为强电磁脉冲响应，E-mail: yb_longzq@163.com

G426

A

1008-0686(2017)02-0094-05