关于FIR滤波器窗函数设计法的若干问题讨论

王艳芬， 张晓光， 王 刚， 刘卫东， 张 林

(中国矿业大学 信息与电气工程学院， 江苏 徐州 221116)

关于FIR滤波器窗函数设计法的若干问题讨论

王艳芬， 张晓光， 王 刚， 刘卫东， 张 林

(中国矿业大学 信息与电气工程学院， 江苏 徐州 221116)

本文针对利用窗函数设计法设计FIR滤波器时所遇到的一些常见问题，例如如何理解吉布斯效应、加窗后的FIR低通滤波器幅度函数特性与IIR滤波器的区别、怎样理解阻带频率和阻带最小衰减、如何进行FIR滤波器指标验证以及利用窗函数法设计线性相位FIR高通滤波器等问题，结合实验设计举例进行了较为详细的讨论和Matlab仿真分析，帮助学生拓展对相关问题的思考，加深对窗函数设计法的理解和应用。

FIR滤波器；窗函数设计法；吉布斯效应

0 引言

“数字信号处理”课程主要学习离散时间信号及系统、离散傅里叶变换(DFT)、快速傅里叶变换(FFT)、IIR滤波器和FIR滤波器两大数字滤波器的设计及数字滤波器网络结构等内容[1-4]。其中窗函数设计法是FIR滤波器设计的重要方法，也是在课程实验中不可缺少的内容，在实际中有着广泛应用[5-8]。我们在多年的教学中发现学生在学习这一内容及在做实验中，容易产生几个比较模糊的问题。例如，如何理解吉布斯效应、加窗后的FIR低通滤波器幅度函数特性与IIR滤波器的区别、怎样理解阻带频率和阻带最小衰减、如何进行FIR滤波器指标验证、利用窗函数法设计线性相位FIR高通滤波器只能采用1型滤波器吗？现就这些问题总结归纳如下，与大家一起讨论和分享。

1 FIR滤波器窗函数设计法原理

窗函数法是设计FIR数字滤波器最常用的方法。这种方法一般是先给定所要求的理想滤波器的频率响应Hd(ejω)，要求设计一个FIR滤波器频率响应H(ejω)去逼近理想的Hd(ejω)。因为利用窗函数法设计FIR数字滤波器是在时域上进行的，所以，必须首先由给定的理想频率响应Hd(ejω)求傅里叶反变换得到对应的单位脉冲响应hd(n)。

因为hd(n)是以纵轴为对称轴的sinc函数，它有两个特点：①它是无限长的序列；②它是非因果的。而要设计有限长(设长度为N)、线性相位的FIR滤波器因果系统，其h(n)必定是因果序列和有限长序列，所以要采取两个措施来得到h(n)：①通过截断将无限长的序列变为有限长的；②通过移位将非因果序列变为因果的。其中截断是通过加窗函数来实现的，正是由于加窗处理，就会产生了以下几个问题。

2 问题讨论

2.1 吉布斯(Gibbs)效应

在学习窗函数法设计FIR滤波器时，首先涉及到一个重要的概念：吉布斯(Gibbs)效应。

什么是吉布斯效应？从数学角度上来说，将具有不连续点的周期函数(如矩形脉冲)进行傅里叶级数展开后，若选取有限项进行合成。选取的项数越多，在所合成的波形中出现的峰值越靠近原信号的不连续点。当选取的项数很大时，该峰值趋于一个常数，大约等于总跳变值的9%。这种现象称为吉布斯效应。

窗函数法是通过加窗对无限长的序列hd(n)截断得到有限长序列h(n)，由于Hd(ejω)是以2π为周期的周期函数，hd(n)可看作Hd(ejω)在频域展为傅里叶级数的系数，所以该方法又称为傅里叶级数法。用有限项傅里叶级数系数去代替无限项傅里叶级数系数，在频率不连续点附近肯定会引起较大误差，则在频域就产生所谓的吉布斯效应。这种效应造成通带和阻带内出现波动，直接影响滤波器的性能，通带内的波动影响滤波器通带中的平稳性，阻带内的波动影响阻带内的衰减，会使设计得到的滤波器满足不了技术上的要求。采用矩形窗设计的滤波器幅度特性如图1所示。

由图1可以看到H(ω)与原理想低通Hd(ω)(虚线矩形)存在两点差别：①H(ω)将Hd(ω)在截止频率处的间断点变成了连续曲线，使理想频率特性不连续点处边沿加宽，形成一个过渡带；②在截止频率πc的两边即ω=ωc±2π/N之处，H(ω)出现最大的肩峰值，肩峰的两侧形成起伏振荡。

直观上，增加窗口宽度N，可能会减小吉布斯效应，但却不然。因为在矩形窗情况下，其幅度函数是一个sinx/x函数(x=ωN/2)，其特点是随x加大(即N加大)，主瓣幅度提高，同时旁瓣幅度也提高，而主瓣和旁瓣幅度相对值不变。所以当截取长度N增加时，只会减小过渡带宽度(4π/N)，但不能改变主瓣与旁瓣幅值的相对比例，即不会改变肩峰值。这个相对比例是由窗函数形状决定的，与N无关。例如，在矩形窗情况下，采用Matlab仿真的结果如图2(a)所示，可清楚看到N增加时，波动并不消失，而是波动振荡变密，最大相对肩峰值则趋于一个常数(约为8.95%)，且最大肩峰值位置越来越接近间断点(此例中，ωc=0.5π)，意味着滤波器的过渡带宽减小。

图1 采用矩形窗设计的滤波器幅度特性

减小吉布斯效应的方法是选取旁瓣较小的窗函数，例如采用汉宁窗、海明窗等。图2(b)是采用汉宁窗在不同N长度下得到的仿真结果。可以看到，通带和阻带内的波动大大减小，滤波器性能得到改善，当然，这是以增加过渡带为代价的。

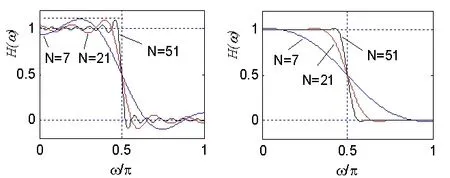
(a) 矩形窗 (b) 汉宁窗 图2 采用不同宽度窗函数设计的滤波器幅度特性

2.2 加窗后的FIR低通滤波器幅度函数特性

理想滤波器对应的单位脉冲响应是非因果的，而因果性是物理系统实现的必要条件，因此只能用一个因果系统去逼近它。另外，也要考虑逼近后系统的容易实现和价格低廉问题，所以实用中的数字滤波器总是在通带和阻带中允许一定的容限，而且在通带与阻带之间有一个过渡带。以一个低通滤波器为例，可以用图3所示容限图来说明。图中δ1为通带的容限，δ2为阻带的容限，ωp为通带截止频率，ωs为阻带截止频率，在ωp与ωs之间为过渡带。

图3 典型IIR低通滤波器的幅频响应

因此，对于低通滤波器的技术指标包括通带截止频率ωp及在ω=ωp处的通带内所允许的最大衰减αp，定义为

αp(dB)=-20lg|H(ejω)|=-20lg(1-δ1)

(1)

此外，还要包括阻带截止频率ωs，及在ω=ωs处的阻带内所允许的最小衰减αs，定义为

αs(dB)=-20lg|H(ejω)|=-20lgδ2

(2)

与IIR滤波器不同，实际FIR滤波器的频率响应是理想低通滤波器的频率响应与窗函数的频率响应的复卷积，卷积的结果使得所设计的滤波器的幅度特性通带和阻带都会出现波动，特别是阻带内会出现偏离零值的负波动。图4给出了加窗后的FIR低通滤波器幅度函数H(ω)特性，与图3不同，H(ω)=1是通带内振幅响应的中间值，通带波纹δ表示振幅响应偏离1的幅度，因此，通带内振幅响应的最大和最小值分别为1+δ和1-δ。H(ω)的正负肩峰是相等的，其绝对值都是δ。如果相对于通带内的中间值H(ω)=1，则与IIR滤波器指标的定义类似，通带最大衰减和阻带最小衰减分别为αp=-20lg(1-δ) dB,αs=-20lgδ dB。

这里要注意的是，图中画出了两个带宽，一个是过渡带宽Δω，是指加窗后滤波器H(ω)的过渡带宽，即从H(ω)=1-δ处衰减到H(ω)=δ处的频率差值，也就是指标中给出的阻带截止频率ωs与通带截止频率ωp之差值，即Δω=ωs-ωp。另外一个带宽Δωw是H(ω)的两个正负肩峰之间的频率差值，它等于窗函数的主瓣宽度。

两个带宽的关系是Δω<Δωw，设计的滤波器性能越接近理想状态即δ越小，两个带宽越接近。两个带宽都与窗长度N成反比，不同窗的比例系数是不同的，如表1所示。

图4 加窗后的FIR低通滤波器幅度函数特性

表1中，旁瓣峰值衰减与阻带最小衰减有联系，但不是一个概念。旁瓣峰值衰减是针对窗函数而言，它是窗谱主副瓣幅度之比，而阻带最小衰减是针对滤波器而言的，当滤波器是采用窗函数方法得到时，阻带最小衰减取决于窗谱主副瓣面积之比。

表1 几种窗函数基本参数的比较

2.3 阻带频率和阻带最小衰减

大家知道，滤波器设计完成时要进行指标验证。IIR滤波器在指标验证时很简单，只需要结合设计的滤波器幅频特性验证在边界频率处(比如阻带频率ωs时所对应的阻带最小衰减αs)是否满足设计要求即可。但用窗函数法设计的FIR滤波器在指标验证时学生往往有一些困惑的地方，比如在给定阻带频率ωs和αs时，仿真结果找到该频率处所对应的值是不是阻带最小衰减αs？在什么情况下它就是阻带内的最大波纹衰减(图4中的大于ωs处对应-δ的dB值)？同一个窗，改变长度N，过渡带在变，ωs处的衰减在变，如何验证设计的滤波器指标？

下面通过一个设计举例来进行该问题的分析。

举例1：用窗函数法设计一个线性相位FIR低通滤波器，设计指标为ωp=0.3π，αp=0.25 dB，ωs=0.5π，αs=50 dB。

首先由阻带衰减决定用什么窗。按照表1，海明窗和布莱克曼窗阻带最小衰减大于50 dB，因为海明窗的过渡带宽小于布莱克曼窗，所以优先选择海明窗。

然后由过渡带决定窗口长度N取多少。按表1过渡带宽Δω=6.6π/N及Δωw=8π/N(下面会说明实际中只需要采用其中一个带宽即可)，让这两个带宽都等于ωs-ωp=0.2π(实际上带宽Δωw用此计算是有近似的)，计算出窗口长度为

窗口长度N改变时得到的滤波器幅频响应仿真波形如图5所示。由仿真图可以看出，当N=N1时，ωs=0.5π处在阻带的边缘，当N>N1且N>N2时，例如取N=45，ωs=0.5π处在阻带内，所对应的阻带衰减值为-52.91 dB，此时该衰减正好等于阻带内的最大波纹衰减。同时可以看到，N的变化基本不影响阻带最大波纹衰减的大小，它只由窗形状决定，而过渡带的宽度则不仅和窗形状有关，且随N的增加而减小，所以调整点数N，实际是在调节过渡带宽，一般调节到ωs处对应衰减等于阻带内的最大波纹衰减时可以得到窗函数设计法最好的性能，因为此时可以做到在满足阻带衰减指标的情况下过渡带达到最窄，如图5(b)所示。

(a) 海明窗 N=33 (b) 海明窗N=45 图5 窗口长度N改变时的滤波器幅频响应

因此，对于窗函数法设计的FIR滤波器指标验证时，与IIR滤波器是不同的，给出以下结论：

(1)用窗函数法设计的FIR滤波器阻带最小衰减通常是指阻带内的最大波纹衰减(图4 中的大于ωs处对应-δ的dB值)，它由窗形状决定，一旦窗函数选定后，阻带最小衰减就是固定的，不受窗长N的影响。

(2)与IIR滤波器不同，用窗函数法设计的FIR滤波器阻带频率ωs和阻带最小衰减αs一般没有直接对应关系，需要通过反复调整窗长和窗形状来达到最佳设计效果，此时可以做到在满足阻带衰减指标的情况下过渡带达到最窄。

(3)窗函数设计法的主要缺点就是通带和阻带的边界频率不易控制，长度N也不易一次决定，要反复多次才能求得满意的结果。也就是说FIR滤波器窗函数设计法不像IIR 滤波器设计那样能精确指定通带和阻带的边界频率及这两个带内的衰减αp和αs，而是有时仅给出截止频率ωc，其它参数是靠长度N及所使用的窗函数的性能来决定的。

此外，也可以看出，窗长N或者说滤波器单位脉冲响应长度的选取主要取决于带宽Δωw，因此一般教材只给出一个带宽，且认为滤波器过渡带宽度近似等于窗函数的主瓣宽度。

注意，按照表1选择海明窗，当N较小，例如N=15时，仿真波形如图6(a)所示，阻带最小衰减为48.21 dB，可以看到，不能满足设计要求50 dB。实际上，表1中所给出的各个窗函数的阻带最小衰减是在N较大(例如N=51)时给出的结果，作为设计FIR滤波器的参考值。所谓N较小，一般是指N大约等于由过渡带宽得到的N值的1/3，例如：按照举例1的过渡带指标，采用Δωw计算，用海明窗和矩形窗时得到的最小N值分别为40和20，它们的1/3约为15和7，此时，得到的阻带最小衰减都比表1中给出的要小，矩形窗得到的结果为18.15 dB，如图6(b)所示。

因此，所谓窗函数选定后阻带最小衰减是固定的，不受窗长N的影响，是指N较大时(可由过渡带求出所需的最小值)，N较小时(此时一定不满足过渡带宽要求了，且ωs处在过渡带中)，阻带最小衰减低于表1中给出的参考值。这也再次说明，设计FIR滤波器时，过渡带和阻带最小衰减都必须要满足设计要求。

(a) 海明窗 (b) 矩形窗图6 不同窗N值较小时的滤波器幅频响应

2.4 线性相位FIR高通滤波器设计

根据线性相位FIR滤波器的单位脉冲响应 的奇、偶对称性以及点数N取值的奇、偶性，分别对应于四种类型线性相位FIR数字滤波器，如表2所示。其中对于高通滤波器的设计，由于H(ω)约束条件的限制，只能选择1型和4型。

表2 四种类型线性相位FIR数字滤波器

问题：当利用窗函数法设计高通滤波器时，有哪些方法?只能采用1型滤波器吗？

(方法一) 利用理想低通滤波器间接设计

在课堂教学中，讲授窗函数设计法原理时都是以设计一个线性相位FIR低通滤波器为例进行的(基本上各教材都是这样叙述的[1-4])。按照窗函数设计思路，假设理想低通滤波器的频率响应为

(3)

其相应的单位脉冲响应为

(4)

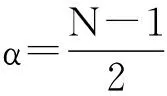
h(n)=hd(n)w(n)

(5)

若设计一个截止频率为ωc的线性相位高通滤波器，可以采用截止频率为ωc=π的低通(即全通滤波器)减去截止频率为ωc的低通滤波器来实现，方法示意图如图7所示。

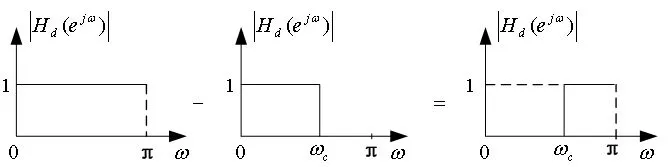
图7 利用全通减低通得到高通滤波器的示意图

根据傅里叶变换的线性性质，频域两个滤波器特性相减，对应时域也是相减，结合式(4)，可以得到理想高通滤波器的单位脉冲响应为

hd(n)|高通=hd(n)|全通-hd(n)|低通

(6)

举例2：设计一个具有下列指标的线性相位FIR高通滤波器：阻带频率ωs=0.6π，αs=50 dB；通带频率ωp=0.75π，αp=0.5 dB。

按照表1，可以选用海明窗。假如ωs-ωp=0.15π=8π/N，得N=53.34 。需要注意的是，因为采用这种方法设计高通，h(n)是偶对称的，所以点数N只能取奇数，即只能采用1型滤波器，N=55时仿真结果如图8(a)。当N取偶数时，在高通的通带π处出现过零，如图8(b)所示，此时显然不能满足设计要求。

(a)N=55为奇数 (b)N=54为偶数 图8 利用理想低通设计高通滤波器结果

(方法二)直接利用理想高通滤波器设计

该方法也称为频谱搬移法[1]。大家知道，一个低频信号乘以(-1)″=cos(nπ)，就可以转换成一个高频信号，这就是“调制性”，时域的调制(相乘)对应于频域的位移，反之亦然。

举例3：采用海明窗设计一个截止频率为ωc=0.5π的线性相位FIR数字高通滤波器[9]。

本题采用上述思路，频域移位对应时域相乘。

设线性相位理想高通滤波器的频率响应为

其相应的单位脉冲响应为

则所设计的高通滤波器的单位脉冲响应为

h(n)=hd(n)wham(n)

其Matlab仿真得到的单位脉冲响应和幅频响应曲线如图9所示。

(a)1型滤波器(h(n)偶对称，N=51为奇数)

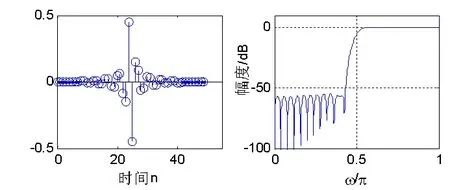
(b)4型滤波器(h(n)奇对称，N=50为偶数)图9利用理想高通设计高通滤波器结果

由此可以看出，直接利用理想高通设计线性相位高通滤波器既可以采用1型滤波器(N取奇数)

也可以采用4型滤波器(N取偶数)，方法比较灵活，均可以达到设计指标要求。

3 结语

窗函数设计法是“数字信号处理”课程中FIR滤波器设计的重要方法。本文针对该方法的一些常见问题结合实验设计举例进行了较为详细的讨论和Matlab仿真分析，可以帮助学生拓展对相关问题的思考，加深对窗函数设计法的理解。

[1] 程佩青. 数字信号处理教程(第三版)[M]. 北京：清华大学出版社，2007

[2] 胡广书. 数字信号处理-理论、算法与实现(第三版)[M]. 北京：清华大学出版社，2012

[3] 吴镇扬．数字信号处理(第二版)[M]. 北京：高等教育出版社，2010

[4] 王艳芬，王 刚，张晓光，等. 数字信号处理原理及实现(第2版)[M]. 北京：清华大学出版社，2013.

[5] 席在芳，周少武， 欧青立, 基于Simulink 的FIR数字滤波器设计实验教学探索与实践[J]. 北京：实验技术与管理，2010，27(5)：80-82.

[6] 欧阳华，尹为民，邵英. 基于比较教学法的FIR数字滤波器设计实验[J].南京：电气电子教学学报，2011，33(1)：75-77.

[7] 申艳，陈后金，薛健. 基于Matlab 加噪语音的FIR滤波器设计[J].南京：电气电子教学学报，2011，33(2)：41-44.

[8] 朱金秀， 张卓，朱昌平. 数字信号处理课程实验教学研究与实践[J] 上海：.实验室研究与探索, 2008，27(5)：96-98.

[9] 王艳芬，王 刚，张晓光，等. 数字信号处理原理及实现学习指导(第2版)[M]. 北京：清华大学出版社，2014.

重要通告

近日来，网上出现假借“电气电子教学学报”投稿系统之名的钓鱼网站，敬请广大作者和读者注意辨识，以免上当受骗。

我刊—电气电子教学学报的官方网址为：http://www.j4eseu.com

联系电话：025-83793107；联系邮箱：j4e@seu.edu.cn

编辑部地址：江苏省 南京市 四牌楼2号 东南大学 李文正楼北404室

Discussion on Some Problems about the Design of Window Function of FIR Filter

WANG Yan-fen，ZHANG Xiao-guang，WANG Gang，LIU Wei-dong，ZHANG Lin

(SchoolInformationandElectricalEngineering，ChinaUniversityofMining&Technology，Xuzhou221116,China)

For the use of the design method of FIR filter encountered some common problems with window function design method, such as how to understand the Gibbs effect, the difference between windowed FIR low pass filter amplitude function characteristics and IIR filter, how to understand the stopband frequency and minimum stopband attenuation, how to verify the FIR filter parameters, using window function method to design linear phase FIR high pass filter is only by type 1 filter, etc，combined with the design example in experiment, a detailed discussion and Matlab simulation analysis are carried out to help students develop the thinking about the related problems and deepen the understanding and application of the window function design method.

FIR filter; window function design method; Gibbs effect

2016-04-23;

2016-06- 24 基金项目：江苏省高等教育教改研究立项课题(2015JSJG275)，教育部第六批国家特色专业建设项目(TS1Z293)，中国矿业大学课程建设与教学改革项目(2014SF04)

王艳芬(1962-)女，博士，教授，主要从事信号处理与通信方面的教学和科研工作,E-mail: lszwyf@163.com

G642.0

A

1008-0686(2017)00-0083-06