系泊系统的设计

王颖俐，王飞，谢文丹

（长治学院 数学系，山西 长治 046011）

系泊系统的设计

王颖俐，王飞，谢文丹

（长治学院 数学系，山西 长治 046011）

文章研究了近浅海系泊系统的设计问题。根据力学的相关原理，利用受力平衡，建立了系泊系统各个部分的受力模型，得到多元非线性方程组，以浮标的吃水深度和游动区域及钢桶的倾斜角度最小为目标，使得系泊系统的各个部位达到最优。

系泊系统；受力平衡；倾斜角度

1 研究背景及问题重述

以2016年全国大学生数学建模竞赛A题为研究背景，研究系泊系统的设计问题，即：为了使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能的小，如何确定锚链的型号、长度和重物球的质量问题。

2 问题的分析

系泊系统要求锚链末端和锚的链接处的切线方向与海床所形成的夹角不能超过16°，否则锚就会被拖行，使得节点移位而丢失。该传输节点的水声通讯系统安装在一个密封的圆柱形钢桶内，其中钢桶长为1 m，外径为30 cm，设备和钢桶总重为100kg。钢桶上接第4节钢管，下接电焊锚链。若要水声通讯设备的工作效果最佳，则钢桶应该竖直。钢桶的倾斜角度，即钢桶与竖直线的夹角超过5°时，设备的工作效果较差。为了控制钢桶的倾斜角度，则需在钢桶与电焊锚链链接处悬挂一个重物球。因此所研究的系泊系统的设计问题就是为了确定锚链的型号、长度和重物球的质量，使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能的小。

首先根据整体分析确定浮标的受力情况。然后再进行局部分析，以水平方向的力为x轴，以竖直方向的力为y轴，建立平面直角坐标系，利用牛顿第一定律，即在合外力为0的情况下物体保持静止，建立系泊系统各个部分的受力模型，以浮标的吃水深度和游动区域及钢桶的倾斜角度最小为目标，通过Maple软件计算，逐步迭代得到。最后利用Maple软件得到锚链形状图为一个类抛物线。

3 模型假设及符号说明

3.1 模型假设

（1）假设海水对整个系统的摩擦力以及各部分之间的摩擦力忽略不计；

（2）假设水声通讯系统正常工作；

（3）假设系泊系统始终能正常工作，且不发生意外状况；

（4）附表中所给的数据真实有效。

3.2 符号说明

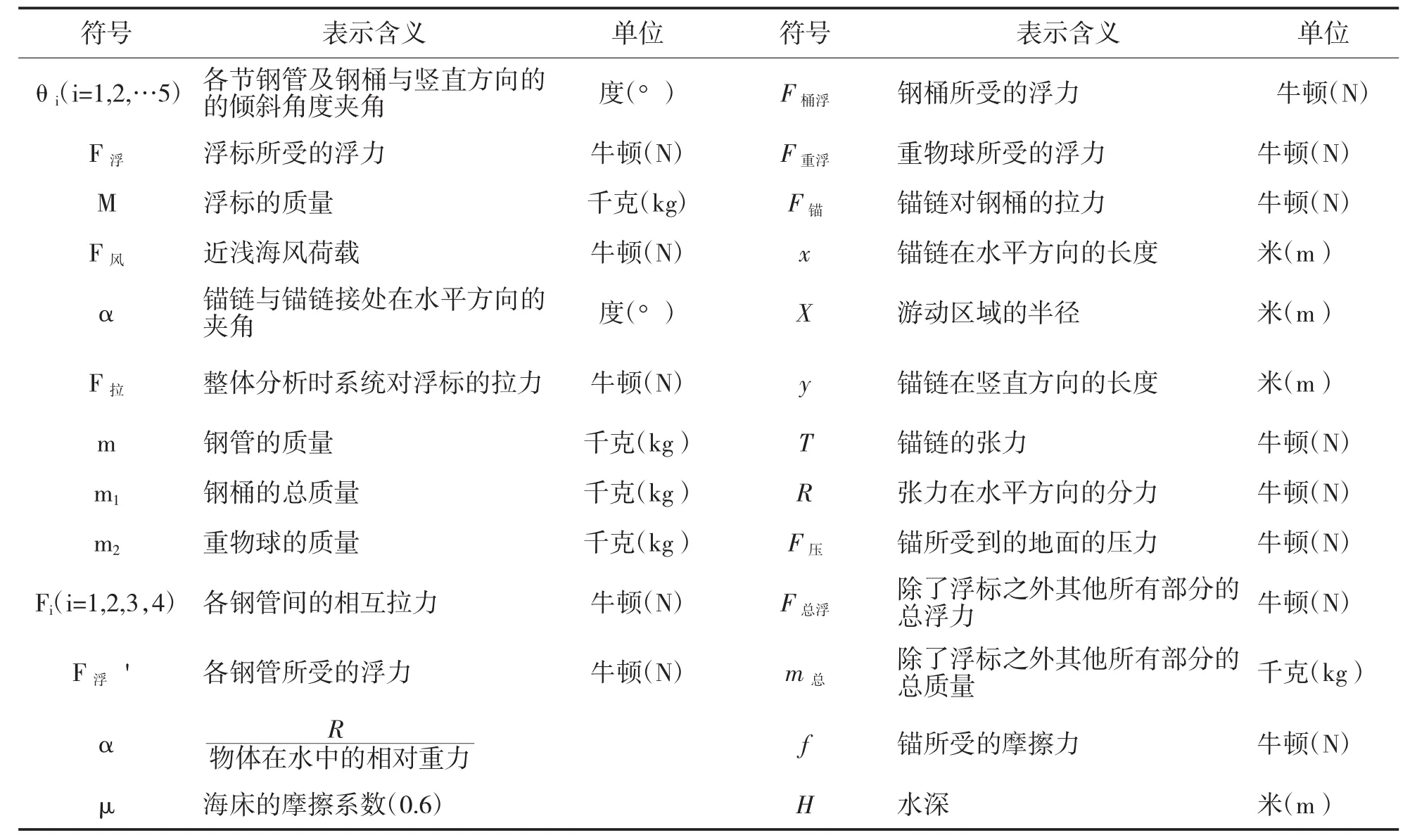
符号 表示含义 单位 符号 表示含义 单位θ（i=1,2,…5） 各节钢管及钢桶与竖直方向的度（°） F钢桶所受的浮力 牛顿（N）i的倾斜角度夹角桶浮F浮 浮标所受的浮力 牛顿（N） F重浮 重物球所受的浮力 牛顿（N）M 浮标的质量 千克（kg） F锚 锚链对钢桶的拉力 牛顿（N）F风 近浅海风荷载 牛顿（N） x 锚链在水平方向的长度 米（m）α 锚链与锚链接处在水平方向的度（°） X 游动区域的半径 米（m）夹角F拉 整体分析时系统对浮标的拉力 牛顿（N） y 锚链在竖直方向的长度 米（m）m 钢管的质量 千克（kg） T 锚链的张力 牛顿（N）m1 钢桶的总质量 千克（kg） R 张力在水平方向的分力 牛顿（N）m2 重物球的质量 千克（kg） F压 锚所受到的地面的压力 牛顿（N）F（ii=1,2,3，4） 各钢管间的相互拉力 牛顿（N） F总浮除了浮标之外其他所有部分的牛顿（N）总浮力F浮＇ 各钢管所受的浮力 牛顿（N） m总除了浮标之外其他所有部分的千克（kg）总质量f 锚所受的摩擦力 牛顿（N）μ 海床的摩擦系数（0.6） H 水深 米（m）α R物体在水中的相对重力

4 模型的建立与求解

利用牛顿第一定律[1]，对系泊系统传输节点进行整体分析和局部分析。首先进行整体分析如图1所示。

图1 传输节点示意图（仅为结构块示意图，未考虑尺寸比例）

如图1所示，每个钢管和竖直方向的夹角和钢桶与竖直方向的夹角，分别用θ（ii=1，2，…5）表示，下面对整体进行受力分析。分析如下：把浮标以下的部位看成悬链线[2]，如图2所示：

浮标受自身的重力Mg，海水对其的浮力F浮，近海风对它的荷载力F风，悬链线的拉力F拉，其中悬链线方程为：

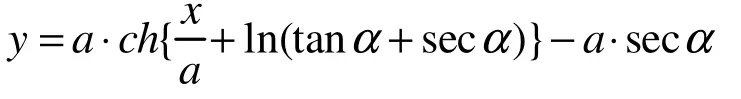
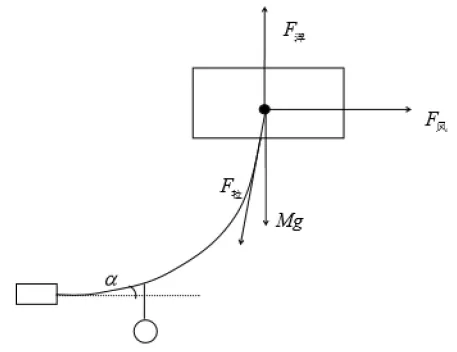
图2 系泊系统整体示意图

悬链线的张力为：

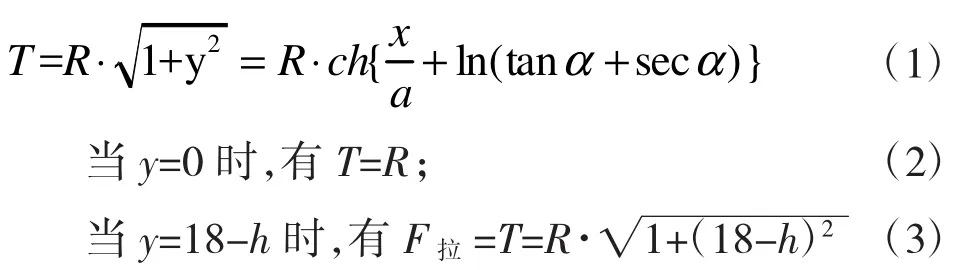
联立（1）（2）（3）式，利用Maple软件计算可得浮标的吃水深度为：

当v=12m/s时，h=0.8008420463m；当v=24m/s时，h=1.050419325m。

再针对局部进行受力分析，分析情况如下表1所示：

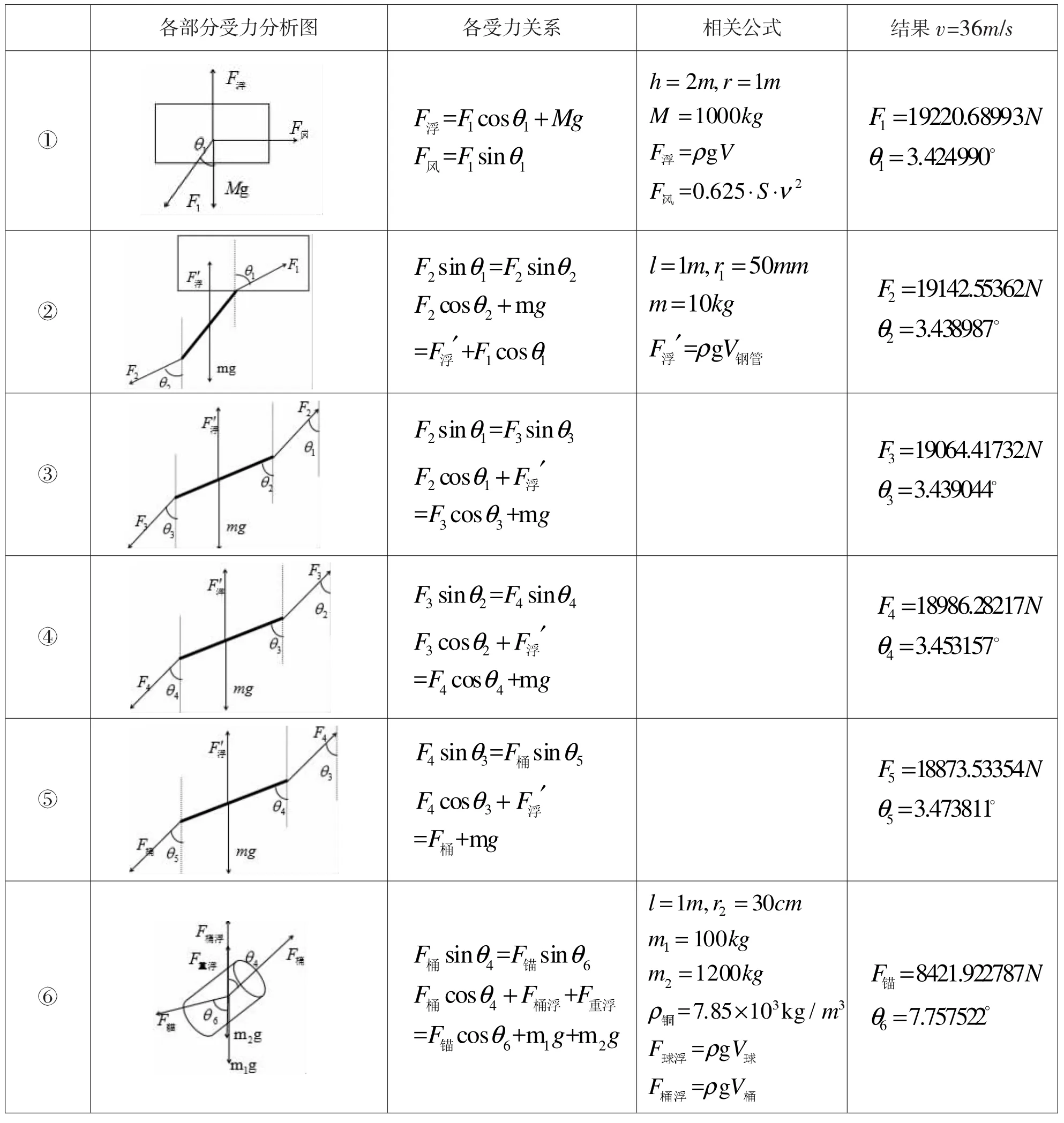
表1 系泊系统各部分受力分析表

根据F锚对锚链的受力进行分析，并将锚链看为一个悬链线，可得方程组：

因此，浮标的游动范围是在海平面上与锚竖直方向相交的点为圆心，X=10.11356613为半径的圆，则所得锚链形状如图3所示，利用Maple软件进行作图，取第二卦限的图像，即为锚链的形状。

图3 V=36m/s时的锚链形状

从上述结果可以看出，当风速为V=36 m/s时，锚链在锚点处与海床的夹角超过了所要求的最大角度16°，使得锚被拖行，导致节点移位丢失，故应调节重物球的质量，使其节点位置不变。通过受力分析画出受力图，如图4所示。

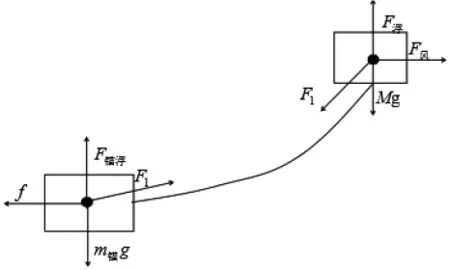
图4 浮标与锚的整体受力分析

根据受力平衡原理，可联立方程组：

解之可得：m=2570 kg

同理可得，要使钢桶的倾斜角度不超过5°时重物球的质量为：m=5285 kg

综上可得，需调节重物球的质量在2570～5285 kg，使得锚链在锚点与海床的夹角不超过16°和钢桶的倾斜角不超过5°。

［1］艾萨克·牛顿（著），赵振江（译）.自然哲学的数学原理［M］.商务印书馆，2006.7.

［2］王丹，刘家新.一般状态下悬链线方程的应用［J］.船海工程，2007，36（3）：26-28.

The Design of Mooring System

Wang Ying-li，Wang Fei，Xie Wen-dan
（Department of Mathematics Changzhi University,Changzhi Shanxi 046011）

This paper studies the design of nearly shallow sea mooring.According to the relevant principles of mechanics,we got the nonlinear multivariable equations by using the principle of force equilibrium.To make any part of the mooring system achieve the optimal,we aimed at minimum of draft depth of buoy,the winding angle area and steel drum.

mooring system;the stress balance;tilt angle

O369

A

1673-2014（2017）02-0006-04

（责任编辑 赵巨涛）

山西省大学生创新项目（2017429）；长治学院科研项目（201514）

2017—02-22

王颖俐（1987— ），女，山西临汾人，硕士，讲师，主要从事时间序列分析及排队论等领域的研究。