频域两尺度下一类Filippov系统的非光滑分析

杨秀芳，张正娣，李绍龙，毕勤胜

频域两尺度下一类Filippov系统的非光滑分析

杨秀芳，张正娣，李绍龙，毕勤胜

(江苏大学理学院，江苏镇江212013)

借助于含非光滑分界面的耦合Bohoffer-Van der Pol(BVP)电路系统，引入周期慢变的交流电源，构建两频域尺度的Filippov系统。利用微分包含理论，分析了尺度因素与非光滑因素相互作用的机理。当周期激励频率远远小于系统固有频率时，选取适当参数，得到了具有滑动结构的复杂周期簇发振荡，并结合理论分析揭示了滑动结构的产生机制。数值结果与理论分析吻合较好。

Filippov系统;频域两尺度;非光滑;簇发;滑动结构

0 引言

非光滑动力系统的研究，越来越引起国内外学者的兴趣和关注。Filippov系统作为一类典型的非光滑动力系统，反映到数学模型上，可以表示为右端不连续的常微分方程(组)，诸多学科领域内的非光滑问题，都可以用此类模型来描述。例如，干摩擦系统［1］、切换电路［2］、生态与经济动力学的阈值［3－4］、电机中的间隙［5］、生物种群的庇护行为［6］和疾病动力学中的媒介效应［7］等。

至今，对Filippov系统动力学行为的研究已取得诸多成果，如文献［8］给出了干摩擦系统分岔与混沌的实验结果。分段线性系统作为一类特殊的Filippov系统，文献［9］研究了参数激励下分段线性两尺度系统的分岔。文献［10］通过施加连续和匹配条件考虑了分段弱非线性振子在周期激励下的对称型周期运动。文献［11］拓展了文献［12］的研究内容，通过尤金等价的思想，利用非光滑分界面相对于两侧光滑向量场的方向导数，在理论上给出了滑动分岔以及擦边分岔的规范型。文献［13］基于Floquet乘子理论，通过引入辅助参数q，分析了激励下的黏滑系统中稳定周期轨道与不稳定周期轨道在非光滑分界面处的动力学行为，指出了周期轨道Floquet乘子跳跃式的穿出单位圆的不连续分岔。但上述研究都是在单一尺度上，并没有考虑广泛存在的尺度因素对这一类典型非光滑系统的动力学行为的影响。

基于此，本文借助一个拓展的具有阈值控制特性的耦合广义Bohoffer-Van der Pol(BVP)电路系统［14］，引入一个慢变交流电源，构建一个两频域尺度的Filippov系统，其无量纲动力学方程表示为:

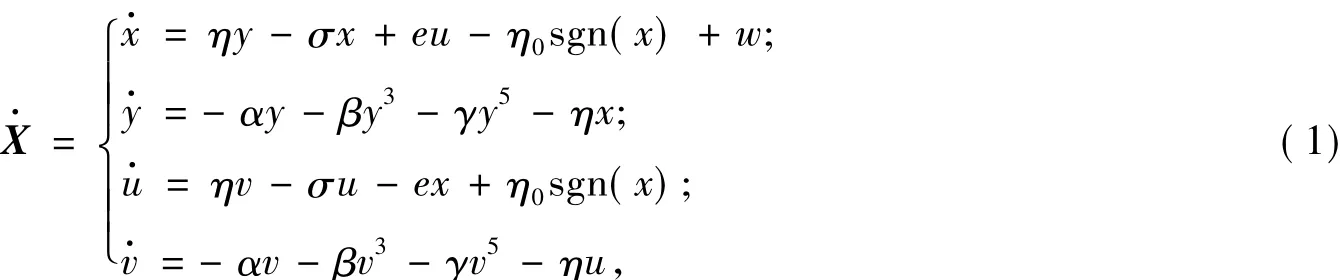
其中:向量X=［xyuv］T;x，y，u，v为状态变量;α，β，γ，σ，η，e，η0为参数。系统(1)中周期激励项w=10Usin(Ωτ)，U和Ω分别为外激励振幅和频率，τ为无量纲时间。

首先通过微分包含理论，探讨尺度因素与非光滑因素之间的相互作用机制，并分析系统(1)在分界面可能出现的动力学行为;然后，选取适当参数，得到了典型的周期簇发振荡，并结合数值结果验证了理论分析的正确性。

1 非常规分岔分析

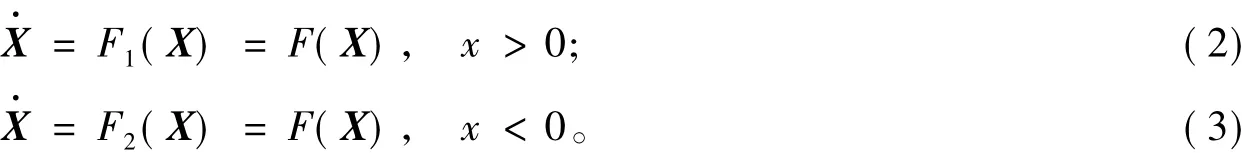
由于系统(1)的向量场不连续，为典型的Filippov系统，借助于微分包含理论，引入辅助参数q∈［0，1］，讨论系统轨线在与非光滑分界面Σx=0接触时的动力学行为，系统(1)可进一步改写为:

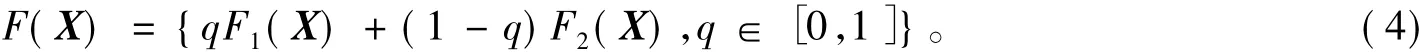
为了明确尺度因素与非光滑因素之间的相互作用关系，在非光滑分界面Σx=0上，定义系统(1)满足x·=0的区域，形式如下:

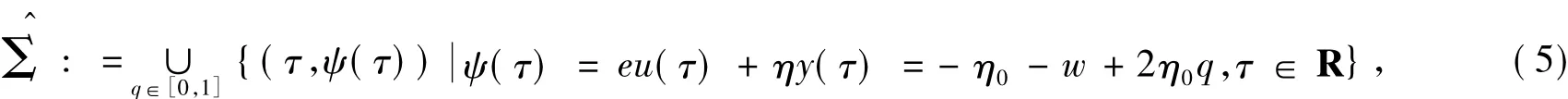
其中:ψ(τ)为eu(τ)+ηy(τ)或－η0－w+2η0q;q为连续闭集。对于任意时刻τ=τ'，假定η0＞0，则集存在上确界与下确界，分别为:

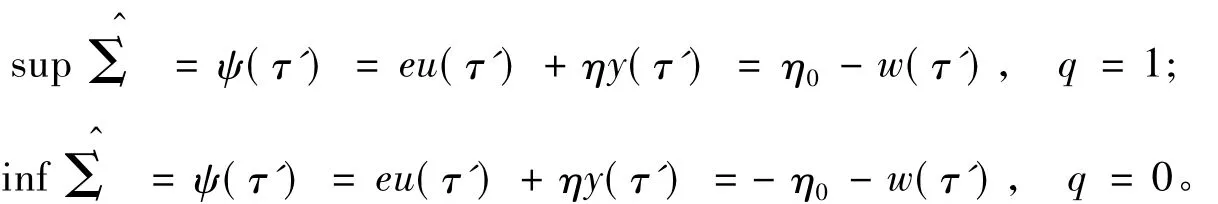
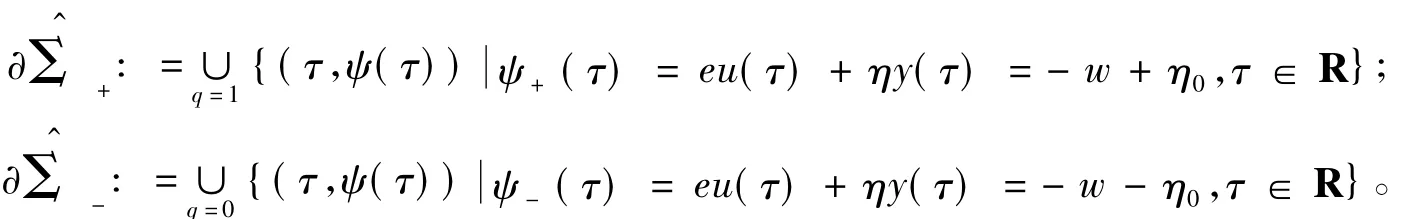
图1为分界面处·x在单个激励周期下的示意图。如图1所示，边界可以将的取值范围在分界面处划分为4个部分:位于边界以上的区域Ⅰ、位于边界以下的区域Ⅲ、边界所围成的区域以及边界本身。不妨假设在时刻τ'，轨线从任意光滑区域到达非光滑分界面显然满足x(τ')=0。下面，根据·x的取值情况，继续讨论轨线在非光滑分界面处的动力学行为。

图1 分界面处x·在单个激励周期下的示意图

首先，根据x(τ')=0时对应的曲线ψ(τ')在图1所处的位置，得到3个确定区域，即轨线将在下一时刻的动力学行为是明确的。当ψ(τ')位于区域Ⅰ:x·＞0，则系统轨线由区域D－到达，并将横截穿过非光滑分界面后进入区域D+运动。当ψ(τ')位于区域，满足x·(τ')=ψ(τ')+ w(τ')－2q'η0+η0=0，其中，q'∈(0，1)满足多值条件，且由于系统状态变量是连续的，则系统轨线将在接下来的一段时间驻留在当ψ(τ')位于区域Ⅲ:x·(τ')＜0，则系统轨线是由区域D+到达，并将横截穿过非光滑分界面后进入区域D－运动。将区域Ⅰ与区域Ⅲ称为横截穿过区域，将区域Ⅱ称为系统的滑动区域。

2 数值验证

选取参数σ=－0.2，η0=4.0，η=2.2，β=－0.8，γ=3.0，α=0.21，e=2.2，Ω=0.01，由于激励频率和系统固有频率之间存在量级上的差异，系统往往会表现出快慢耦合的动力学行为，即簇发振荡。当U=10.0时，系统的轨线与非光滑分界面Σx=0接触，并呈现出一个自身关于原点对称的周期簇发振荡，如图2所示。

图2 系统(1)在U=10.0时的周期簇发振荡

图2a给出了系统U=10.0时，在(w，x)平面逆时针运动的周期簇发振荡的转换相图及其与系统平衡曲线的叠加图，图2b为对应的状态变量x的时间历程图。数值结果显示:整个周期簇发振荡包含了两个激发态SP±和两个沉寂态QS±，如图2b所示。通过对系统常规分岔的计算可以发现:由超临界Hopf分岔B1±、B2±和B5±(如图2a中的三角形所示)生成的稳定极限环SC1±与SC2±(如图2a中细实线所示)，导致轨线围绕平衡线(如图2a中粗实线所示)振荡(激发态)，而这里的亚临界Hopf分岔B3±与B4±使得平衡线的稳定性发生改变，加上平衡线此时上下方向存在一定距离，导致轨线出现跳跃现象，处于激发态。轨线在越过分岔点B1±后，逐渐收敛到平衡线上并沿着平衡线运行(沉寂态)。

结合上述对于系统轨线接触非光滑分界面时可能出现的动力学行为的分析，揭示整个周期簇发振荡中出现的两种不同滑动结构的形成机制。图3给出了一个振荡周期内的时间历程、滑动边界与曲线ψ(τ)的叠加图。

图3 时间历程、滑动边界与ψ(τ)的叠加

首先，结合数值结果来讨论位于激发态中的“从分界面一侧进入分界面-滑动-返回分界面同一侧”滑动结构的成因。假设以位于激发态SP－的点A1－为整个周期簇发振荡的起始点，随着轨线的运行，如图3a右上角的局部放大图所示，在τ0时刻，轨线首次由光滑区域D－到达分界面，对应时刻的曲线ψ(τ0)在此时落在滑动区域内部，由于系统变量的连续性，轨线将在分界面内运行一段时间，出现滑动现象。而在时刻τ1，曲线ψ(τ)与滑动边界横截相交，并在此后进入横截区域Ⅲ，导致轨线随后脱离分界面并返回光滑区域D－。由数值结果可以发现，轨线在激发态SP－中多次呈现出从区域D－进入分界面-滑动-返回区域D－的滑动振荡模式，其成因与轨线在时间区间［τ0，τ1］相同。相应地，轨线在激发态SP+中多次出现从区域D+进入分界面-滑动-返回区域D+的滑动振荡模式，其原因可相似地分析。

可见，轨线在整个周期簇发振荡中出现的两种滑动结构:“从分界面一侧进入分界面-滑动-返回分界面同一侧”与“进入分界面-滑动-穿过分界面”，数值结果和本文的理论分析吻合较好。

3 结束语

对于周期外激励下Filippov系统，当外激励频率远远小于系统的固有频率时，系统存在频域两尺度。把整个周期外激励项看作一个慢变参数，利用微分包含理论，根据尺度因素与非光滑因素之间的相互作用机制，采取时间序列的分析法，分析了系统在非光滑分界面处可能出现的动力学行为。在数值验证中，得到了系统具有滑动结构的复杂周期簇发振荡，其滑动结构的产生与理论分析吻合较好。

［1］张有强.干摩擦碰撞振动系统的非线性动力学研究［D］.兰州:兰州交通大学，2008.

［2］陈章耀，王亚茗.切换电路时间对非线性切换系统振荡特性的影响［J］.河南科技大学学报(自然科学版)，2016，37(5):87－90.

［3］BERNARDO M D，VASCA F.Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters［J］.IEEE transactions on circuits＆systems-part I(fundamental theory＆applications)，2000，47(2):130－143.

［4］BOR Y J.Uncertain control of dynamic economic threshold in pest management［J］.Agricultural systems，2003，78(1): 105－118.

［5］ZHOU Z，TAN Y，XIE Y，et al.State estimation of a compound non-smooth sandwich system with backlash and dead zone［J］.Mechanical systems＆signal processing，2016，83:439－449.

［6］CHEN X，HUANG L.A Filippov system describing the effect of prey refuge use on a ratio-dependent predator-prey model［J］.Journal of mathematical analysis＆applications，2015，428(2):817－837.

［7］WANG A，XIAO Y A.Filippov system describing media effects on the spread of infectious diseases［J］.Nonlinear analysis hybrid systems，2014，11(1):84－97.

［8］CSERNK G，STPN G.On the periodic response of a harmonically excited dry friction oscillator［J］.Journal of sound＆vibration，2006，295:649－658.

［9］陆慧玲，李绍龙，张正娣.参数激励下分段线性两尺度系统的分岔［J］.河南科技大学学报(自然科学版)，2015，36(6):71－74.

［10］JI J C，HANSEN C H.Approximate solutions and chaotic motions of a piecewise nonlinear oscillator［J］.Chaos，solitons＆fractals，2004，20(5):1121－1133.

［11］COLOMBO A，BERNARDO M D，HOGAN S J，et al.Bifurcations of piecewise smooth flows:perspectives，methodologies and open problems［J］.Physica d(nonlinear phenomena)，2012，241(22):1845－1860.

［12］FEIGIN M I.The increasingly complex structure of the bifurcation tree of a piecewise-smooth system［J］.Journal of applied mathematics and mechanics，1995，59(6):853－863.

［13］LEINE R I，CAMPEN D H.Bifurcation phenomena in non-smooth dynamical systems［J］.European journal of mechanicsa (solids)，2006，25(4):595－616.

［14］WU X P，WANG L C.Codimension-2 bifurcations of coupled BVP oscillators with hard characteristics［J］.Applied mathematics＆computation，2013，219(10):5303－5320.

O29

A

1672－6871(2017)05－0065－05

10.15926/j.cnki.issn1672－6871.2017.05.014

国家自然科学基金项目(11472115，11472116)

杨秀芳(1990－)，女，江苏南京人，硕士生;张正娣(1972－)，女，江苏丹阳人，教授，博士，博士生导师，主要研究方向为非线性动力学.

2017－03－01