基于云模型与证据理论的故障诊断方法*
李少波,陈永前(贵州大学.现代制造技术教育部重点实验室;b.机械工程学院,贵阳550025)
基于云模型与证据理论的故障诊断方法*
李少波a,b,陈永前a
(贵州大学a.现代制造技术教育部重点实验室;b.机械工程学院,贵阳550025)
针对单一传感器无法对复杂设备进行故障诊断和证据理论难以合理获取BPA的问题,提出了一种基于云模型与证据理论的多传感器数据融合故障诊断方法;首先求取每个故障模型下各个特征参数的云模型参数,建立故障诊断云模型知识库;然后结合云模型知识库,求取各个测量参数的隶属度值,并转换为各个诊断证据体;最后通过证据理论组合规则将各个证据进行融合,在融合决策条件下求出诊断结果。实验结果表明,该方法能合理并有效地对复杂设备进行故障诊断。
云模型;证据理论;故障诊断;数据融合
0 引言
故障诊断技术往往是通过传感器对设备或产品进行监测,采集其状态数据,并在一定的判定规则下,通过与专家知识库进行对比判断,从而决断出故障的所在。在设备与产品都逐渐趋于复杂的今天,引起故障的因素也越来越复杂,同一故障可能会是不同的多个因素引起的,一个因素也可能引起多个故障的发,这些故障的复杂性、多样性以及相互关联性成为故障诊断的一大特征。同时由于传感器自身精度与测量范围的约束,以及测量环境的影响、测量方法的局限性等因素,使采集来的信息具有模糊性、不确定性乃至错误性。这决定了单一传感器难以对复杂设备与产品进行故障诊断。
证据理论是由Dempster和Shafer提出并完善而来的。它是一种不确定推理的数学方法,在处理不确定信息融合与故障诊断方面得到很大的应用与研究[1-4]。文献[1]将一种改进的证据理论应用于对齿轮故障诊断过程中,提高了故障诊断的正确性;文献[2]将D-S证据理论应用于电机机械故障诊断,通过融合各类特征的信息来提升了故障诊断结果的准确性;文献[3]用D-S证据理论对轨道电路的微调电容进行故障诊断,提高了诊断的准确性。文献[4]研究了证据理论在复合故障诊断中的应用,综述了证据理论在故障诊断中的研究情况,并提出了将证据理论与其他方法结合使用的思想。然而,在利用证据理论进行故障诊断过程中,往往会因为某些传感器测量信息错误而产生证据间的高冲突问题,从而影响了融合结果的正确性,因此,正确地获取证据的赋值函数(BPA)是故障诊断结果正确与否的关键。
基于此,本文引入云模型理论,利用云模型善于处理模糊性、不确定性和随机性的特点,实现对传感器信息向证据理论的基本概率赋值的转化,完善证据理论正确地获取赋值函数难的问题,为故障诊断提供更合理的决策。
1 相关知识介绍
1.1 云模型
云模型是在随机数学和模糊数学的基础上发展而来,实现模糊集理论中的模糊性和概率论中的随机性的有机结合,可以用来统一刻画语言值中大量存在的随机性、模糊性以及两者之间的关联性[5]。
设U是一个用数值表示的定量论域,C是U上的定性概念,若定量数值x∈U是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0,1]是具有稳定倾向的随机数,即:

则x在论域U上的分布称为云(cloud),记为C(x),每一个x称为一个云滴,云模型便是由多个云滴所组成。
云模型中用期望Ex、熵En和超熵He这3个数字特征来表示信息的模糊性和不确定性的数学性质[6-7]。期望Ex代表这个定性概念的点,反映云滴群的平均点;熵En反映了定性概念中的模糊性和随机性,并揭示了二者之间的关联性,是定性概念的不确定性度量;超熵He是熵的不确定性度量,即熵的熵,反映云滴的凝聚度。在故障整定过程中,对云模型三参数的求取是确定基本概率赋值的重要前提。
1.2 证据理论
证据理论是一种不确定推理的数学方法,在处理不确定信息融合方面有很好的优势。证据理论的详细介绍可以参照文献[8-10],此处仅对证据理论的组合规则进行说明。
设Θ为一个辨识框架,若对AΘ,有mi(i= 1,2,…,n)为Ai(i=1,2,…,n)的n个基本概率分配,则证据理论的组合规则为:

2 云模型——证据理论的故障诊断方法
所谓故障诊断,就是将传感器采集到的特征参数跟模板库中的故障特征参数进行匹配,从而得到故障类型的过程。本文中将云模型理论与D-S证据理论有机地结合,其中云模型理论主要是实现对不同诊断数据的统一建模,并求取各个传感器特征参数的基本概率赋值;而D-S证据理论则用于对各个传感器的的基本概率赋值进行融合处理。基于云模型与D-S证据理论的故障诊断流程图如图1所示。
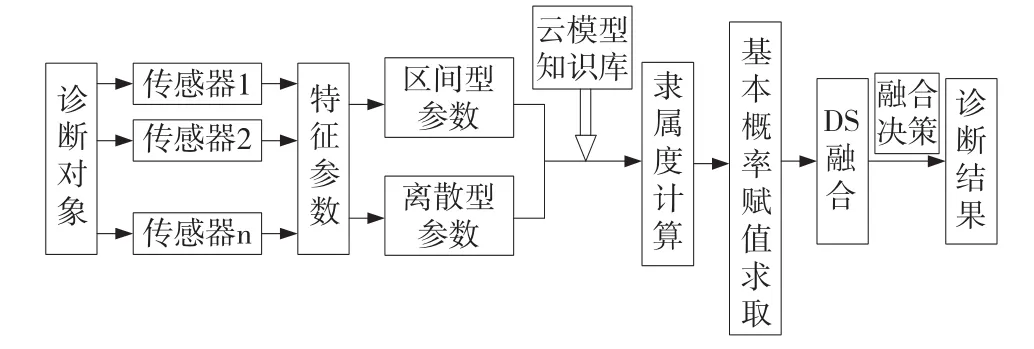
图1 基于云模型与证据理论的故障诊断流程图
2.1 云模型下的故障隶属度计算
设有n类故障θ1,θ2,…θn,在每一类故障θi下都有m个特征指标参数X(θi)=(xi1,xi2,…,xim),xij表示在第i类故障下的第j个参数,每个参数都可以用云模型来表示。由于传感器类型及监测的要求不同,其采集来的数据有不同的类型,主要表现为区间型变量和离散型变量。同时,在故障诊断时,大多参数都服从正态分布,故可以使用正态云进行建模。
对于区间指标变量而言,不同的故障模式下可能出现不同的区间取值,假定在第k种故障模式下测得故障模式信号中区间值为[Cmin(k),Cmax(k)],即为该故障模式下的双边约束,则可设期望值为约束条件的中值,主要作用区域为双边约束区域的云来近似建模,参数计算如下:

式中,Exij、Enij、Heij分别为第i类故障下的第j个参数云模型的期望值、熵值和超熵值,一般由实验获取。
对离散型指标而言,在某一故障模式下的某个特征参数xij的云模型参数可以通过实验方法获得。在假如第i类故障的第j个参数下,测得r个数据(xij1,xij2,…xijr),则云参数可以由如下计算得到:

式中,Exij、Enij、Heij的意义与区间型指标变量中的相类似。
当确定了故障诊断云模型的各个参数后,通过多个传感器对诊断对象进行特征参数采集,得到的数据集X=(x1,x2,…,xm),其中xi(i=1,2,…,m)为被诊断对象的第i个特征参数,便可求得被诊断对象的每个特征参数相对于云模型的隶属度值。其计算公式为[11]:
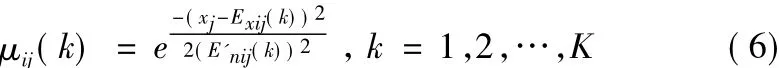
式中,μij(k)表示被诊断对象的第j个特征参数相对于云模型模板库中的第i类故障下第j个特征的第k次诊断的隶属度;E'nij(k)为以熵值Enij(k)为期望,Heij为标准差所产生的一个正态随机数。当k大于1时,特征参数为多个值的情况下(传感器多次采集数据),故障诊断中的第j个特征参数相当于云模型故障库中地i类故障下第j个特征参数的隶属度可由k个隶属度值中的最大值确定:
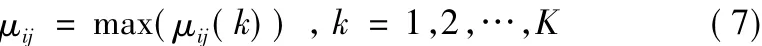
同时,考虑到故障诊断过程中的传感器精度、测量误差、外界干扰等原因,会引起传感器测量的不确定性,不确定性的隶属度可由下式获得:

式中ψj为第j个特征参数不确定度的隶属度值。当求得所有参数的隶属度后,可以得到隶属度矩阵:
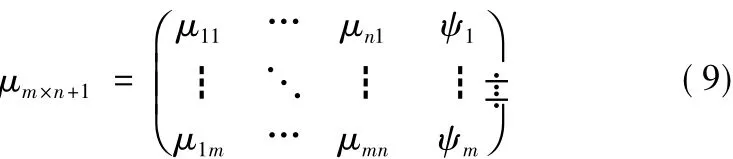
2.2 基本概率赋值(BPA)确定
设识别框架Θ=(θ1,θ2,…,θn),对于指标k的一个测量值V,该测量值隶属于各故障库云模型的程度分别为μij,则该测量值的基本概率赋值可以用以下方法求得:
在隶属度矩阵中,每一行数列μij(j为定值,i= 1,2,…,n)可表示为各种故障模式下对同一特征参数值的隶属度,即一个故障诊断传感器一次诊断采集的数据对每种故障模式的隶属度。因此,对隶属度矩阵的每一行进行归一化处理可得到各特征参数的基本概率赋值:
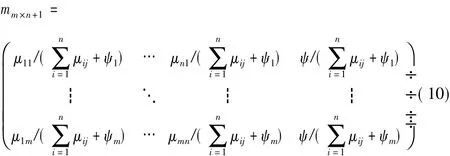
2.3 融合诊断决策
通过对故障诊断对象的云模型的建立、隶属度及基本概率赋值求解,便可利用证据理论组合规则的各条证据进行融合。但在对故障做出判断时,应还需一定的融合判定准则[12]:
设Θ为一个辨识框架,θ1和θ2是辨识框架Θ的两个元素,若满足m(θ1)=max{m(θi),θiΘ},则故障诊断决策的基本准则为:

式中,m(Θ)为不确定情况下的证据值,λ1、λ2、λ3为门限阀值,本文取值分别为0.7、0.01、0.5。
3 故障诊断实例分析
下面以数控机床故障诊断为例,对本文方法的可行性和有效性进行验证。根据实际故障诊断经验和专家知识库,规定数控机床的故障模式机床状态正常θ1、主轴转速过大θ2、刀具磨损量较大θ3,刀具磨损量大,并且主轴转速业过大θ4,则组成的故障模式辨识框架为Θ={θ1,θ2,θ3,θ4}。
在确定故障模式辨识框架后,便可通过采集的数据进行故障诊断。首先利用三个加速度传感器x1,x2,x3对某数控机床的床身、主轴和刀架的进行故障监测,并在数控机床处于不同的故障模式下进行数据采集;然后将采集来的数据进行整理和处理,求出不同故障模式下的不同参数的云参数;此处应用文献[13]中的实验数据,对其处理后求得不同故障模式下的云模型参数如表1。
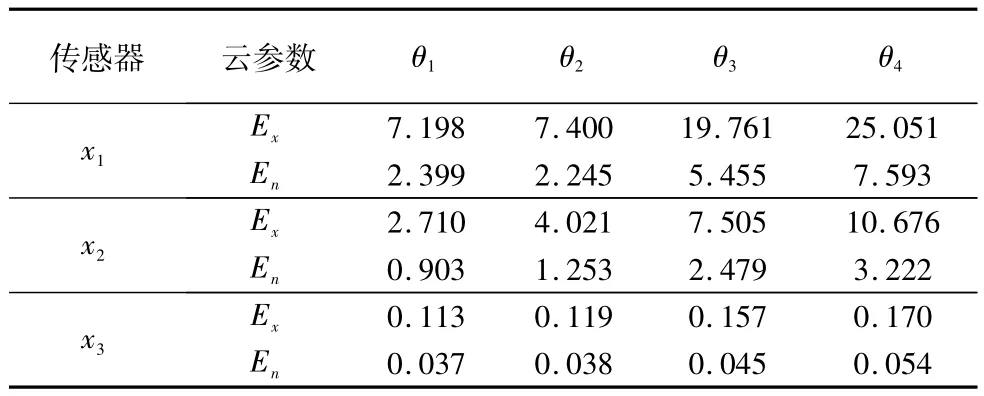
表1 不同故障下的云参数值(He=0.2)
求得各个云参数后,按照式(6)~式(8)便可求得不同故障模式下不同传感器的隶属度值。我们取某次实验三个传感器的采集值(x1,x2,x3)=(16.054,7.505,0.136),求得不同故障模式下的不同传感器的隶属度值见表2。
按照式(10)对隶属度进行归一化处理求取隶属度矩阵,得到不同故障下各传感器的基本概率赋值见表3。
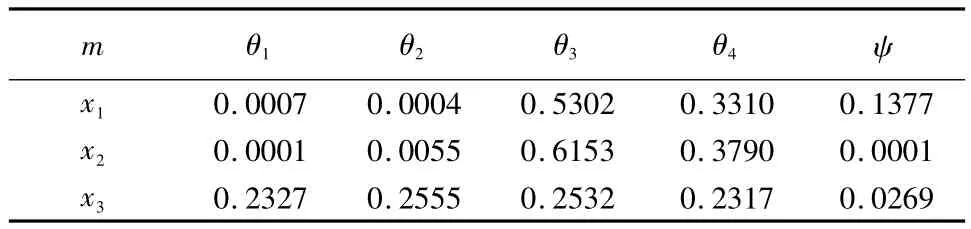
表3 基本概率赋值
将求得的基本概率赋值按照证据理论融合规则式(2)进行融合得到诊断结果见表4。

表4 故障诊断融合结果
由融合结果可以看出,若仅仅使用单一传感器采集的数据进行诊断,由表3可以得到,传感器x1均不能满足2.3节中的三个门限的要求,传感器x2不能满门限2的要求,传感器x3不能满足1和3两个门限的要求,故通过单一传感器无法对故障进行诊断。而利用本文方法,由表4结果可知有82.65%的概率为刀具磨损量较大θ3,远大于其他故障下的概率值,且不确定度ψ值仅为0.01%,完全满足2.4节中的故障诊断决策,能有效地决断出对数控机床的故障所在。同时,利用文献[13]的方法对本文数据进行诊断比较,得到文献[13]方法计算值为(0.730、0.875、0.984、0.626),将其归一化处理得到(0.2271、0.2721、0.3062、0.1946),可见文献[13]的方法得到的各个故障模式下的值都较相近,结果可信度不高。因此,本文方法能有效地解决单一传感器对故障诊断的局限性和不确定性,并且该方法诊断的总体不确定度仅为0.0001,是一种有效的故障诊断方法,具有一定的实际工程应用价值。
4 结论
本文将云模型理论与证据理论相结合,提出了一种基于云模型和证据理论的故障诊断方法。该方法利用云模型善于处理离散性、随机性和模糊性数据的特点,对故障诊断数据进行处理,解决了证据理论正确合理地获取基本概率赋值的难题;并结合证据理论对各个基本概率赋值进行融合得到故障诊断的结果。通过对数控机床故障诊断的实验结果表明,该方法具有较高的故障诊断率和较低的不确定性,克服单一传感器和一些现存方法在故障诊断中的不足,为复杂设备及产品故障诊断领域提供参考。
[1]刘希亮,陈桂明,李方溪,等.基于改进证据理论的齿轮泵故障诊断方法研究[J].机械科学与技术,2014,33(2): 183-188.
[2]Yang B S,Kim K J.Application of Dempster-Shafer theory in fault diagnosis ofinduction motors using vibration and current signals[J].Mechanical Systems and Signal Processing,2006,20:403-420.
[3]Oukhellou L.Fault diagnosis in railway track circuits using Dempster-Shafer classifier fusion[J].Engineering Applications of Artificial Intelligence,2010(23):117-128.
[4]雷高伟,张清华,马春燕,等.证据理论在复合故障诊断中的应用研究[J].组合机床与自动化加工技术,2014(2): 75-78.
[5]李德毅,刘常显.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.
[6]Naylor J,Gilmore M S,Thompson R L,et al.Compar-ison of objective supercell identification tec-hniques using an idealized cloud model[J].Monthly Weather Review,2012,140 (7):2090-2102.
[7]张仕斌,徐春香.基于云模型的信任评价方法研究[J].计算机学报,2013,36(2):422-431.
[8]He Y,Hu L F,Guan X,et al.New method for measuring the degree of conflict among general basic probab-ility assignments[J].Science China Information Sciences,2012,24 (31):159-165.
[9]邵景峰,贺兴时,王进富,等.大数据环境下的仿织制造执行系统设计[J].机械工程学报,2015,51(5):160-170.
[10]Guo K,Li W.Combination rule of D-S evidence theory based on the strategy of cross merging between evidences[J].Exp-ert Systems with Applications,2011,38(10): 13360-13366.
[11]王守信,张莉,李鹤松.一种基于云模型的主观信任评价方法[J].软件学报,2010,21(6):1341-1352.
[12]FAN X F,ZUO M J.Fanlt diagnosis of machines based on D-S evidence theory in gearbox fault diagnosis[J].Pattern Recognition Letter,2006,27:377-385.
[13]李遇春.基于贝叶斯网络的数控机床远程智能故障诊断研究[D].杭州:浙江大学,2010.
(编辑李秀敏)
A Fault Diagnosis Method Based on Cloud Theory and Evidential Theory
LI Shao-boa,b;CHEN Yong-qiana
(a.Key Laboratory of Advanced Manufacturing Technology,Ministry of Education;b.School of Mechanical Engineering,Guizhou University,Guiyang 550025,China)
Aiming to the problem of single sensor cannot make a fault diagnosis for complex equipment and evidence theory is difficult to make a reasonable BPA,the paper proposed a multi sensor data fusion fault diagnosis method based on cloud modeland evidence theory.Firstly,taking the cloud modelparameters of various characteristics under each faultmodel,and establishing the cloud modelknow ledge base for faultdiagnosis;Then combining w ith the cloud model know ledge base to obtaining the membership values of various measurement parameters,and transform it as each diagnosis evidence;finally,all the evidence is fused by the combination rule of evidence theory,and the diagnosis results are obtained under the condition of fusion decision.Experimental results show that the method is effective and accurate for the fault diagnosis of complex equipment.
cloud model;evidential theory;fault diagnosis;data fusion
TH16;TG506
A
1001-2265(2017)04-0099-04
10.13462/j.cnki.mmtamt.2017.04.025
2016-06-30;
2016-08-05
国家自然科学基金资助项目(51475097);贵州省基础研究重大项目(黔科合JZ字[2014]2001)
李少波(1973—),男,湖南岳阳人,贵州大学博士生导师,博士,研究方向为制造物联、智能故障诊断,(E-mail)lishaobo@gzu.edu.cn;通讯作者:陈永前(1991—),男,贵州毕节人,贵州大学硕士研究生,研究方向为数字化设计制造,(E-mail)chenyq620@163.com。

