双螺母预紧滚珠丝杠副轴向静刚度与扭转变形关系研究*

黄金宝，荣乾锋，欧屹，祖莉(南京理工大学机械工程学院，南京210094)

双螺母预紧滚珠丝杠副轴向静刚度与扭转变形关系研究*

黄金宝，荣乾锋，欧屹，祖莉
(南京理工大学机械工程学院，南京210094)

为了研究扭转变形对滚珠丝杠副轴向静刚度影响，对双螺母预紧滚珠丝杠副的滚珠进行动力学分析，并考虑接触角的变化，建立滚珠丝杠副扭转变形数学模型。使用滚珠丝杠副摩擦力矩试验台、静刚度试验台对双螺母预紧滚珠丝杠副进行摩擦力矩、静刚度检测。结果表明:滚珠丝杠副刚性测量中对丝杠进行扭转补偿后，测量结果更加合理、准确;滚珠丝杠副刚性测量中，丝杠被测长度越长，丝杠产生的扭转变形越大，对滚珠丝杠副轴向静刚度测量结果影响越大。

滚珠丝杠副;轴向静刚度;扭转变形;摩擦力矩

0 引言

滚珠丝杠副为数控机床关键滚动功能部件，广泛应用于数控机床进给系统［1-3］。滚珠丝杠副刚性是数控机床进给系统动态稳定、振动幅度的重要影响因素［4］。随着滚珠丝杠副速度和载荷的不断提高，其振动问题愈加突出，严重影响数控机床的定位精度，滚珠丝杠副刚度不足严重阻碍数控机床向高速化、高精度方向发展［5］。

目前，滚珠丝杠副刚性的研究大多集中在滚珠丝杠副静刚度的影响因素分析、静刚度建模及有限元仿真上。Kazuki TAKAFUJI以双螺母滚珠丝杠副为研究对象，综合考虑丝杠轴、螺母、丝杠螺纹的弹性变形等因素，建立新型滚珠丝杠副静刚度数学模型，并通过试验进行验证分析［6］。陈勇将分析滚珠丝杠副刚度影响因素，考虑接触角的变化及接触变形影响，建立联合载荷下滚珠丝杠副刚度数学模型，并通过试验验证理论模型的可靠性［5］。周福兴对力加载系统工装和位移测量系统工装的设计做了详细讨论［7］。然而，上述研究在进行刚性试验时并未考虑丝杠的扭转变形对刚性的影响，且丝杠的被测长度不同，其扭转变形量不同。为了研究滚珠丝杠副刚性试验中不同被测长度与扭转变形关系，本文考虑了接触角的变化，对双螺母预紧滚珠丝杠副的滚珠进行动力学分析，建立滚珠丝杠副扭转变形模型，并通过试验分析滚珠丝杠副扭转变形对刚性的影响程度。

1 双螺母预紧滚珠丝杠副扭转变形数学模型

1.1 坐标系转换

为了便于分析，本文采用坐标转换矩阵的理论方法来描述滚珠丝杠副系统中各个部件之间的相对位置，(x，y，z)为固定坐标系，z轴与丝杠轴线所在的方向一致;(xr，yr，zr)为旋转坐标系，该坐标系与丝杠具有相同的转速，轴也与丝杠轴线所在的方向一致。在滚珠球心处建立Frenet坐标系(t，n，b)，t轴方向与球心轨迹螺旋线在球心o处的切线方向重合，n轴方向与丝杠在滚珠球心o径向方向重合，β表示滚珠丝杠副的螺旋角，θ表示滚珠相对于丝杠旋转的角度，Ω表示旋转坐标系(xr，yr，zr)相对于固定坐标系(x，y，z)的旋转角度。

图1 滚珠丝杠副空间坐标系

固定坐标系(x，y，z)与旋转坐标系(xr，yr，zr)转换关系为:

旋转坐标系(xr，yr，zr)与Frenet坐标系(t，n，b)之间的转换关系为:

式中:θN中N=L时表示左侧螺母中滚珠，N=R表示右侧螺母中滚珠;

1.2 滚珠与滚道间的接触角

根据国际标准BS ISO3408-4规定，滚珠丝杠副刚性检测时，外加轴向载荷Fa=30%Ca，(Ca为滚珠丝杠副额定动载荷)。经检测，国内外滚珠丝杠副预紧力皆小于其30%Ca，当外加轴向载荷Fa=30%Ca时，双螺母预紧滚珠丝杠副滚珠受力分析如图2所示。由于滚珠丝杠副各个部件为材料性能相近的钢材，因此丝杠滚道与螺母滚道结构参数可近似看成相同，则同一螺母滚道中滚珠与丝杠滚道、螺母滚道接触变形量近似相等，且接触角也近似相等，αL表示左侧螺母1滚珠与滚道间的接触角，αR表示右侧螺母2与滚道间的接触角;δ表示滚珠接触变形量(N表示螺母;S表示丝杠;L表示左侧滚珠;R表示右侧滚珠)。

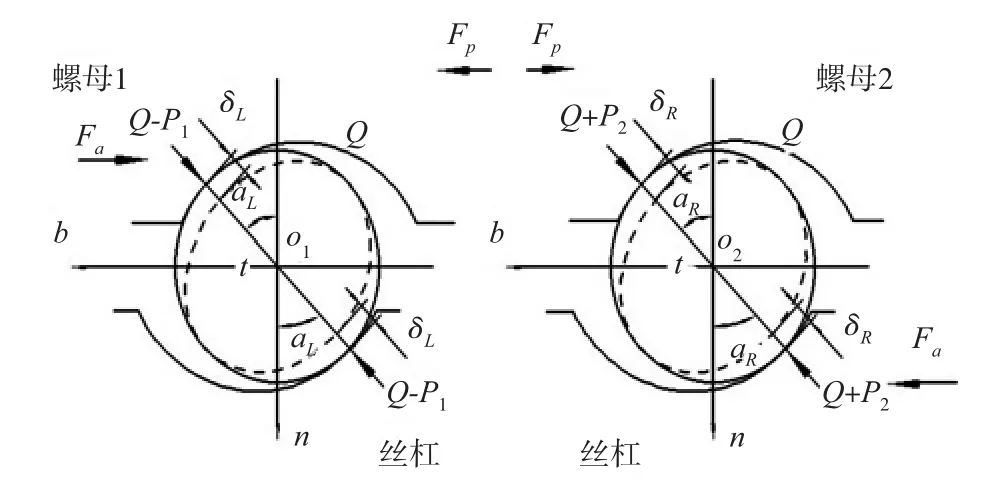
图2 双螺母预紧滚珠丝杠副滚珠受力分析

假设螺母固定不动，当丝杠受到轴向力Fa时，螺母1受到的预紧力减小量为F1，螺母2受到的预紧力增加量为F2。同时滚珠受到的法向载荷也发生了变化，Q表示丝杠副仅受预紧力Fp时滚珠受到的法向载荷，P1、P2分别表示丝杠在轴向载荷作用下滚珠1、滚珠2受到的法向载荷。设左侧滚珠1所受法向载荷为QL，右侧滚珠2所受法向载荷为QR，则有:

式中:FL表示左侧螺母1受到的预紧力;FR表示右侧螺母2受到的预紧力。

当双螺母预紧滚珠丝杠副仅受预紧力作用时，设滚珠1、滚珠2与螺母1、螺母2的初始接触角为α0，取α0=45°。由丝杠轴线方向受力平衡关系可得:

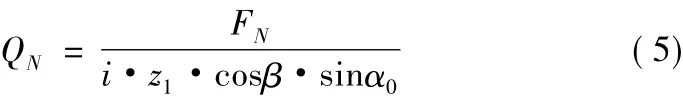
式中:N取L或R。

滚珠丝杠副预紧力与摩擦力矩之间的关系式为［8］:

式中:μ为摩擦系数;rs为丝杠半径;rb为滚珠半径; Mtest为实际检测的摩擦力矩。

滚珠与滚道间的接触变形满足赫兹接触理论，则有:

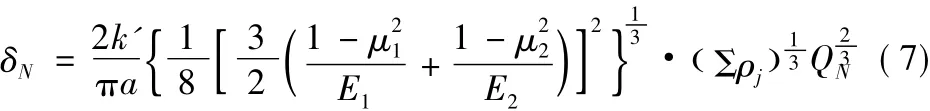
式中:、k'、a是Hertz系数;μ1、μ2是两接触弹性体的泊松比;E1、E2为两接触弹性体的弹性模量;Σρj为两弹性接触体在接触点处的综合曲率;QN表示滚珠受到的法向载荷(N=L表示滚珠1所受法向载荷，N=R表示滚珠2所受法向载荷);δN表示滚珠与滚道接触变形量(N=L表示滚珠1与滚道接触变形量，N=R时表示滚珠2与滚道接触变形量)。

根据丝杠和螺母滚道中心螺旋线的半径不变，并结合式(1)、(2)可列出如下关于αj、r、βi的3元非线性方程组［9］:

式中:Cθ表示cos(θ)，Cαj表示cos(αj)，Sβj表示sin(βj)，Sαj表示sin(αj)，Sθ表示sin(θ)，Tβj表示tan(βj);rs、rn分别表示丝杠、螺母滚道半径;rcs、rcn分别表示丝杠、螺母滚道中心螺旋线底圆半径;rb表示滚珠半径;r表示丝杠公称半径;Ph为丝杠导程。

随着轴向载荷的不断增加，滚道和滚珠局部的几何参数均发生变化，从而导致接触角的变化。接触区域几何参数变化如下:

式中:N取L或R。

联立公式(5)～公式(8)，采用Newton非线性迭代法可求出变化的αj、P1、P2。

1.3 丝杠扭转变形

由图2知，滚珠1、滚珠2受到的法向载荷QL、QR在Frenet坐标系中表示为:

设滚珠与丝杠的接触点到丝杠轴线的距离为l［8］，则:

由于滚珠丝杠副刚性测量过程中，螺母固定不动，丝杠与螺母之间不发生相对旋转，所以Ω=0。而不同的滚珠对应不同的θ(第1个滚珠对应的θ为0，第2个滚珠对应的θ为2×2π/z1，第n个滚珠对应的θ为n×2π/z1)，左右螺母中滚珠作用于丝杠上的力对丝杠产生的扭矩分别为:

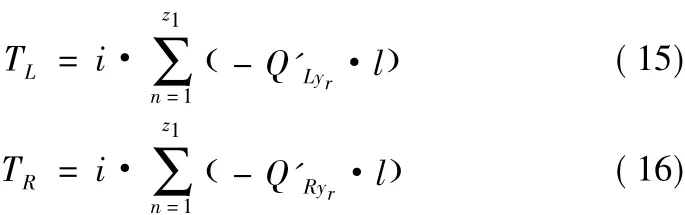
式中:Q'Lyr

、Q'Ryr分别表示Q'L、Q'R在旋转坐标系yr轴上的分量。

滚珠作用于丝杠上的力对丝杠产生的总扭矩为:

滚珠丝杠受到扭矩T作用产生的扭转角为:

式中:G为滚珠丝杠材料剪切弹性模量;T为左右螺母中所有滚珠作用于丝杠上的力产生的扭矩;l'为螺母中心到丝杠轴端受力处距离;Ip为滚珠丝杠极惯性矩，Ip=πd4/32，d为滚珠丝杠螺纹内径，d=33.65mm。

扭转变形角φ引起的轴向位移为:

考虑丝杠扭转补偿后，滚珠丝杠副轴向静刚度为:

式中:λno表示为无扭转补偿时丝杠相对于螺母的轴向位移。

2 试验

本次试验选取的双螺母预紧滚珠丝杠副(型号为R40-10k4-FDC)具体参数如表1所示。

表1 滚珠丝杠副参数表

2.1 滚珠丝杠副摩擦力矩测量原理

目前，滚珠丝杠副预紧力无法直接测量获得，一般通过测量摩擦力矩来计算预紧力。目前，出厂后的滚珠丝杠副的摩擦力矩标称值仅仅只是其摩擦力矩平均值。由于滚珠丝杠副行程误差的影响，不同位置处的摩擦力矩均不相同，对应的预紧力和刚性值也均不相同。因此，为了准确获得刚性测量位置处的摩擦力矩和预紧力，需要测量滚珠丝杠副有效行程内的摩擦力矩变化曲线。摩擦力矩测量原理如图3所示，丝杠一端与伺服电机相连，另一端固定在尾座中心。螺母的圆周运动受到连杆①与悬臂②的约束，支撑单元与丝杠滚道相接触，当丝杠转动时，螺母和工作台可同时沿丝杠轴线方向往返运动。试验前，先对压力传感器③进行标定，然后使用100号润滑油让丝杠跑合5min，确保滚珠丝杠副充分润滑;试验过程中，丝杠以100r/min的转速进行摩擦力矩测量。

图3 滚珠丝杠副摩擦力矩测量原理

2.2 滚珠丝杠副静刚度测量原理

目前，滚珠丝杠副静刚度测量过程中没有考虑丝杠的扭转变形。因此，本文对滚珠丝杠副静刚度测量系统进行了优化，优化后的测量系统主要由移动横梁、压力传感器、丝杠防转装置、刚度测量装置组成，如图4所示。针对滚珠丝杠副静刚度测量过程中丝杠发生旋转的现象，设计了丝杠防转装置，结构如图5所示。上压盘1与连杆4通过螺钉连接，连杆4与下压盘2中对应的孔相配合，丝杠5与下压盘2之间通过平键6连接，钢球3起到轴向负载的传递作用。因此，当移动横梁缓慢加载时，通过连杆4与平键6的作用，可以防止丝杠发生旋转。为了测量丝杠的扭转变形量，设计新型刚度测量装置，该装置中设有4个接触式位移传感器(型号:Pretec 2940N)，其中3个传感器检测丝杠受外加轴向力状态下的轴向变形，3个传感器成120°均匀分布。剩余的1个传感器用来检测丝杠受外加轴向力状态下的扭转变形，通过该传感器可得到静刚度测量过程中丝杠发生的扭转变形量。

图4 滚珠丝杠副静刚度测量系统

图5 滚珠丝杠副防转装置

为了研究不同位置处丝杠扭转变形对滚珠丝杠副轴向静刚度的影响，根据国际标准BS ISO3408-4规定，使用30%Ca的力对丝杠轴端进行加载(螺母固定)，最终利用最小二乘法对外加载荷与轴向变形进行刚度曲线拟合。本试验中，在滚珠丝杠副有效行程内选取5个测量点，每个位置点进行5次轴向静刚度检测。

3 结果分析与讨论

由于滚珠丝杠副存在加工误差，其有效行程内的摩擦力矩存在波动。型号为R40-10k4-FDC的滚珠丝杠副摩擦力矩如图6所示，摩擦力矩波动范围为1.19N·m～1.33N·m。由于滚珠丝杠副静刚度测量时，测量装置在安装时存在一定误差，因此，不同位置处的摩擦力矩值取该位置点左右10mm范围内的平均值，根据公式(6)即可得到双螺母预紧滚珠丝杠副不同位置点处的预紧力值。

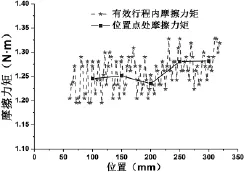
图6 滚珠丝杠副摩擦力矩

滚珠丝杠副静刚度试验中检测到的旋转变形包括防转装置中平键的周向变形、丝杠副自身间隙引起的旋转变形及丝杠扭转变形，它们的关系为:

式中:φtest表示试验中检测到的旋转变形;φ1表示平键的周向变形;φ2表示丝杠副自身间隙引起的旋转变形;φ表示丝杠扭转变形计算值。不考虑丝杠扭转变形量时丝杠的旋转变形量，φ1+φ2。结合施加的轴向载荷便可求得滚珠丝杠副不同位置的轴向静刚度。扭转补偿后，滚珠丝杠副轴向静刚度较之补偿前更加接近于理论值(根据BS ISO3408-4计算获得)，测量数据更加合理、准确，如图7所示。且随着测量距离(螺母中心到丝杠轴端受力处的距离)增加，轴向静刚度的变化幅度也增加，如图7所示，变化幅度从100mm处的2.5%到300mm处的7.7%，变化趋势基本成线性关系。试验表明，滚珠丝杠副轴向静刚度检测时，丝杠螺母中心距离丝杠轴端受力处越远，扭转变形对轴向静刚度的影响越大。

图7 扭转补偿前后滚珠丝杠副轴向静刚度及其变化幅度

需要说明的是，在位置250mm处，滚珠丝杠副轴向静刚度与其他位置处相比较低，可能由于该段处丝杠的导程误差或材料等原因(见图7)，导致此处的滚珠产生的轴向变形较大，使得丝杠相对于螺母的整体轴向位移较大，最终使得该点的轴向静刚度较低。

4 结论

本文通过对双螺母预紧滚珠丝杠副滚珠进行动力学分析，考虑接触角的变化，建立滚珠丝杠副扭转变形数学模型，并通过试验分析丝杠扭转变形对滚珠丝杠副轴向静刚度的影响。试验结果表明:

(1)考虑扭转变形，对滚珠丝杠副刚性测量进行扭转补偿后，测量结果更加合理、准确;

(2)滚珠丝杠副刚性测量中，丝杠被测长度越长，丝杠产生的扭转变形越大，对滚珠丝杠副轴向静刚度影响越大;本文研究结论不仅适用于双螺母预紧滚珠丝杠副，同样也适用于单螺母滚珠丝杠副。该研究结论对滚珠丝杠副轴向静刚度测量具有十分重要的意义。

［1］XU Z Z，Liu X J，Kim H K，et al.Thermal error forecast and performance evaluation for an air-cooling ball screw system［J］.International Journal of Machine Tools and Manufacture，2011，51(7－8):605－611.

［2］Wei C C，Lai R S.Kinematical analyses and transmission efficiency of a preloaded ball operating at high rotational speeds［J］.Mechanism and Machine Theory，2011，46 (7):880－898.

［3］许向荣，宋现春，姜洪奎.提高数控机床滚珠丝杠进给系统机械刚度的措施［J］.组合机床与自动化加工技术，2008(8):1－4.

［4］Feng G H，Pan Y L.Investigation of ball screw preload variation based on dynamic modeling of a preload adjustable feeddrive system and spectrum analysis of ball-nuts sensed vibration signals［J］.International Journal of Machine Tools＆Manufacture，2012，52(1):85－96.

［5］陈勇将，汤文成，王洁璐.滚珠丝杠副刚度影响因素及试验研究［J］.振动与冲击，2013，32(11):70－74.

［6］Takafuji K，Nakashima Katuhiro.Stiffness of a ball screw with consideration of deformation of the Screw，Net and Screw thread.Preloaded double nut［J］.Jsme International Journal，1990，33(4):.620－626

［7］周福兴，王禹林，韩军，等.滚珠丝杠副刚性试验台加载及测量系统工装设计［J］.组合机床与自动化加工技术，2016(4):113－116.

［8］Zhou C G，Feng H T，Chen Z T，et al.Correlation between preload and no-load drag torque of ball screws［J］.International Journal of Machine Tools＆Manufacture，2016 (102):35－40.

［9］胡建忠，王民，高相胜，等.双螺母定位预紧滚珠丝杠副轴向接触刚度分析［J］.机械工程学报，2014，50(7): 60－69.

(编辑李秀敏)

Investigation of the Correlation between the Axial Static Stiffness and the Torsional Deformation of the Double-nut Preloaded Ball Screw Mechanism

HUANG Jin-bao，RONG Qian-feng，OU Yi，ZU Li
(School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China)

In order to study the influence of the torsional deformation on the axial static stiffness of the ball screw mechanism，the kinetics of the double-nut preloaded ball screw mechanism w as analyzed firstly，and then taking the changes of contact angle into consideration，the mathematical model based on the torsional deformation of the ball screw mechanism was established.The friction torques of the double-nut preload ball screw mechanism was measured on the ballscrew friction torque testbench.And the axialstatic stiffness of the ball screw was also measured on the ball screw stiffness test bench.The test results agree well with our theoretical analysis and the results showed that，w ith the compensation of the torsional deformation，the measurement results are more reasonable and accurate.And in the process of rigidity measurement of the ball screw mechanism，with the increasing of the measured length of the screw，the torsional deformation is also increased，w hich has a greater impacton the measurementresults of the ballscrew axialstatic stiffness.

ball screw;the axial static stiffness;torsional deformation;friction torque

TH166;TG506

A

1001－2265(2017)04－0034－04

10.13462/j.cnki.mmtamt.2017.04.009

2016－07－20;

2016－07－30

国家科技重大专项(2014ZX04011031)

黄金宝(1987—)，男，江苏沭阳人，南京理工大学硕士研究生，研究方向为滚珠丝杠副刚性与综合性能测评，(E－mail)459252447@qq.com;通讯作者:欧屹(1982—)，男，南京人，南京理工大学讲师，博士，研究方向为滚动功能部件性能检测，(E－mail)ouyi3281289@163.com。