借助平面直角坐标系实现线段长度的计算转化

摘 要：借助平面直角坐标系，将线段长度的求法分为两类：一是平行于坐标轴，二是不平行于坐标轴；在初中学段不允许应用两点间坐标公式的前提下，通过数形结合、化归思想及类比思想，较好解决线段长度的求法应用问题。

关键词：求线段长度；平面直角坐标系；数形结合；化归思想；类比思想

授人以鱼不如授人以渔，在数学教育教学中，作为老师，更加应该教授给学生的是数学的魅力，而魅力之处就是数学思想方法。初中学段，要求不允许使用两点间坐标公式，所以我们借助平面直角坐标系，将线段的位置关系作为分类标准，分为两类，通过几何的构造与代数结合，从而解决线段长度的求法问题。

一、数形结合建系求线段长

一般地，我们需要知道一条线段的长度，可以采用两种基本的方法，一是通过生活经验进行对比、丈量、估值；二是通过直尺等工具进行丈量。在数学计算中，如果遇到动点问题或者是有条件缺失的情况下，特别在初中学段的很多二次函数动点题中，则更加需要掌握利用数形结合的方法解决此问题了。

数形结合就是建立在数形优势互补基础上，抓住数与形之间本质上的联系，以“形”直观地表达数，以“数”精确地研究形的思想方法，其实质就是讲问题抽象的数量关系与直观的图形结构结合起来进行考虑，既分析其代数意义，又揭示其几何直观，使数量的精确刻画与空间形式的直观形象巧妙、和谐地结合在一起，充分利用这种结合，寻找解题思路的一种思想；具体而言，就是根据问题的具体情况，把具有直观形式的图形性质的问题转化为具有算法性质的数量关系的问题，通过代数方法分析数量关系来探讨、论证、揭示直观图形的性质，从而使抽象思维和形象思维结合起来，使复杂问题简单化，抽象问题具体化，化难为易，使问题得到解决。

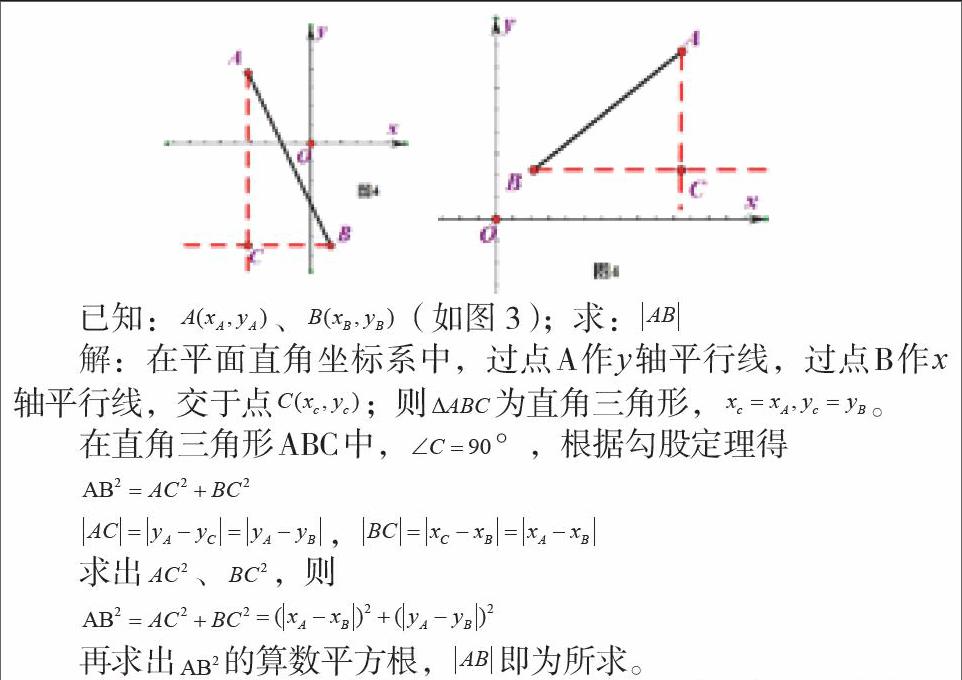
建立平面直角坐标系，由于在平面直角坐标系中，每一个位置都可以用一对有序数对进行表达，即一个点的坐标（横坐标、纵坐标），从而实现线段的长度代数化。在一个平面直角坐标系中，有无数条线段，。不难发现，所有的线段可以被分为两大类，第一是平行于坐标轴，第二是不平行于坐标轴。由于一条线段有两个端点，将线段放入平面直角坐标系后，这两个端点就是两个点，存在着这两个端点各自的横坐标、纵坐标；由此便实现线段的长度代数化的转化。

分析：运用类比的思想方法。类比是一种间接推理的方法，也是一种科学研究的方法。类比是通过两类不同对象A、B间的某些属性的相似，而从A具有某种其他属性便猜想B也是这种属性。所以，党线段AB平行于y轴时，其长度为两点纵坐标之差，为满足非负数的线段长度，故“上—下”。

二、化归思想探究转化

第二类：线段的位置关系——不平行于坐标轴

笛卡尔说过：“任何一个几何问题都很容易化归为用一些术语来表示，使得只要知道直线段的长度的有关知识，就足以完成它的作图。”“化归”是“转化和归结”的简称。化归方法是数学问题解决的一般方法，其基本思想是：把待解决的问题，通过某种转化手段，归结为易解决的另一个或一些问题，通过后者问题的解决，而获得原问题的解决。

显然，当线段与坐标轴平行时，我们很容易可以通过分析得到线段长度的代数坐标计算表达，可以当不平行时，情况就较为复杂啦。要考虑的问题就有许多，不平行，倾斜程度如何，有没有什么特殊點可以构造等。所以采用化归思想，把不平行的位置关系想办法转为第一类平行时的位置关系即可。

总结，所线段AB不平行于坐标轴，则它的线段长度的代数表达仍然只有线段的两端点坐标有关系，由此解决问题。

从数学教学角度讲，一堂课往往新就新在思维过程上，高就高在思想性上，好就好在学生参与活动的深度和广度上。有思想深度的课，给学生留下长久的心灵激荡和对知识的深刻理解，以后即使具体的知识忘了，但数学地思考问题的方法将长存，这样的数学教学才具有真正的实效和长效，真正能提高人的数学素养。

参考文献：

[1]顾泠沅.作为教育任务的数学思想与方法[M].上海：上海教育出版社，2009：9、11、280、302.

[2] 张雄、李得虎.数学方法论与解题研究[M].北京：高等教育出版社，2006：364.

[3]何君青.例谈代数问题中的几何解法[J].初中数学教与学， 2015（5）：61-63.

作者简介：杨周荣麟，云南师范大学实验中学数学中职教师。从教以来担任班主任和数学教学工作，所带班级荣获“2015～16学年昆明市级先进班集体光荣称号”；多次获“优秀班主任”、“先进教育工作者”称号；所教班级成绩优异，数学成绩经常年级第一、第二，优秀率较高，所教学生喜爱数学。曾获全国师范大学讲课比赛二等奖；云南师大讲课比赛特等奖、实验现场教案设计一等奖、课件制作一等奖等。