挖掘数学之美，拓展通识视域*

郭培俊（浙江工贸职业技术学院，浙江温州325003）

挖掘数学之美，拓展通识视域*

郭培俊
（浙江工贸职业技术学院，浙江温州325003）

为研究改变高职数学教学现状，把美育作为切入点。高职数学的美育按照不同的面向可分为四个层次分层递进：数学通识要泛美；高等数学要渗美；专升本数学要拣美；数学建模要求美。挖掘高职数学美的元素，充实数学教育内涵，拓展通识教育新视野，数学美育实为一种一举多得的教学策略。

高职数学；美育；通识教育；分层递进

高职教育改革已步入深水区，教育理念也相应发生转变：唯“重技能、快就业”是瞻的短期功利思想，放眼成“重素养、强通识”为学生一生考虑的终身教育理念，通识课程变成核心课程，大学教育包括高等职业教育回归到培养人的这一终极目的上来。开发覆盖面广、整合性强的通识课程是当下乃至今后高职教育教学改革的重要任务之一，两门或多门课程的有机整合是一条成功并值得借鉴的建设途径。比如清华大学开发的《艺术与审美》《基础社会科学》（包括心理学、社会学、政治学）都是课程建设成功的范例。数学作为大学通识教育的重要课程之一，把它与美学融合在一起是一个很美的设想与课题。浙江工贸职业技术学院（以下简称工贸学院）在通识教育改革研究中，就此进行了专题立项研究。课题从挖掘高职数学及数学教学中的美元素着手，进而开展数学与美育、数学与人文的融合研究，以美启真，以美创新，对高素质创新人才培养是非常有意义的，对改变高职数学教学现状是一种颠覆性的突破。

一、高职数学美育的背景及意义

（一）生源特点

高职学生层次低、差异大、学习数学兴趣淡。高职招生情况路人皆知，学生学习数学索然无味，教师越教越郁闷。激发学生学习数学兴趣势在必行。

（二）素质需要

工贸学院通识教育研究院院长邱开金教授提出了“三通”教育理念，即“通智通识通人”，是高职院校实施通识教育的捷径之一。高职不仅仅培养工匠，而是培养具有创新精神的高素质的大国工匠。

改变高职数学教学现状的最佳切入点之一便是——美育，通过美育唤醒学生学习数学的兴趣[1]。爱美之心人皆有之；哪里有数哪里就有美（普罗克洛斯）。数学课堂实施美育具有悠远的渊源性和广泛的普适性。由于种种原因，部分学生对数学不感兴趣，但这种现状是可以改变的。“认为数学枯燥乏味的人，只是看到了数学的严谨性，而没有体会出数学的内在美”（数学家华罗庚）。让学生学会欣赏美、鉴赏美，继而创造美，也是实现素质教育的需要[2]。

二、数学美育的途径

数学美是一种严肃的冷峻的深沉的美。根据高职数学教学的内容和特点，高职数学美育的途径可采取：分层递进式。

高职院校开设的数学课型有：数学通识，高等数学，专升本数学和数学建模。按照开课的面向和普及程度，其相应的美育方式和内容也有所区别。按照参与人数多少可以用一个金字塔模型来表示，如图1所示。

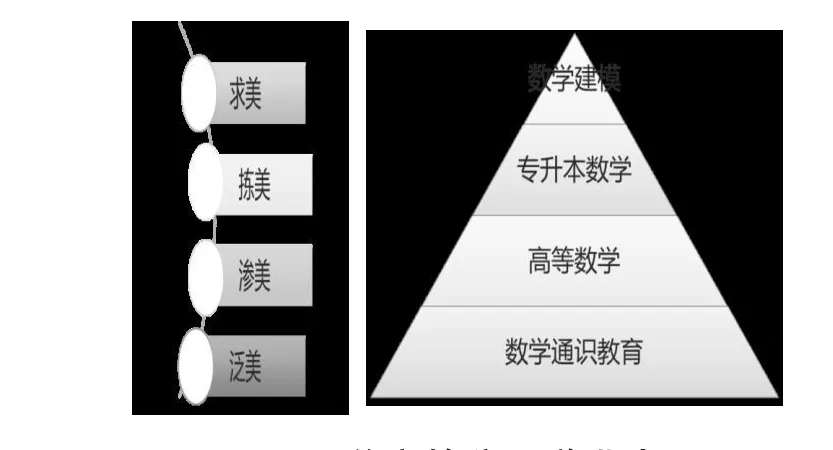
图1 美育的分层递进式

三、数学美育的内容

(一)数学通识教育的美育——泛美[3]

数学通识作为一门文化通识课程，可以开设美育专讲，处处体现数学之美。其内容包含：

1.中小学数学美育的概述

针对中小学数学中出现的数学美（代数、几何、函数）通过数形结合方式进行补偿性回顾，分两类小结，让学生对数学的内在美和形式美有一个感性认识，形成数学美的初步概念，为高等数学的美育作铺垫。

和谐美：统一、规律、对称、平衡、一致、简捷。

奇异美：超越、意外、特解、无限、反常、猜想。

2.黄金比率的拓展

设计程序和内容包括：最美五角星→相似三角形→黄金比→大自然的优乐美（向日葵、松果）→探索发现（兔子问题：斐波拉契数列）→应用1（穿高跟鞋的学问）→应用2（演讲的最佳位置）→应用3（照相取景焦点）→应用4（文学音乐高潮点）→应用5（建筑装饰）→应用6（炒股个案）。

3.音乐中的美学

世界是数字的和谐；宇宙是音乐的载体。音乐是跳动的数学，数学是凝固的音乐。“数还可以把世界转化为和我们心灵相通的音乐”（圣奥古斯汀）。数学中的音乐美育设计如下：

（1）毕达哥拉斯音乐数。从人们知道的勾股数3、4、5，提出问题：音乐数是哪三个数？引出毕达哥拉斯的音乐数3、4、6；再说明为什么把这三个数字称为音乐数。介绍基本乐理常识：3/6=1/2八度音，4/6=2/3五度音，3/4四度音，其公因数为3、4、6。

（2）伯努利螺旋线。乐理上为解决任意转调问题，人为地把八度音按等比序列分成12个相等半音。若按等差数列，八度音应该分成14个半音，但音乐里要求只能分成12个半音，如何分呢？其数学原理如下：这个方程近似成立（逼近思想）的最优正整数解为m=12,n=7。方程解的音乐意义即是：一个音程的7个全音可以分成12个相等的半音。也就是我们熟知的3（咪）到4（发），7（唏）到高音1（哆）之间是半音，而其他两个相邻的音阶之间是全音的乐理常识了。

为了推广十二音律，音乐家巴赫找到了当时的数学家伯努利。伯努利一针见血地指出用对数螺旋线来表示十二平均音律的模型，恰如其分，巧夺天工，优美无比，如图2所示。

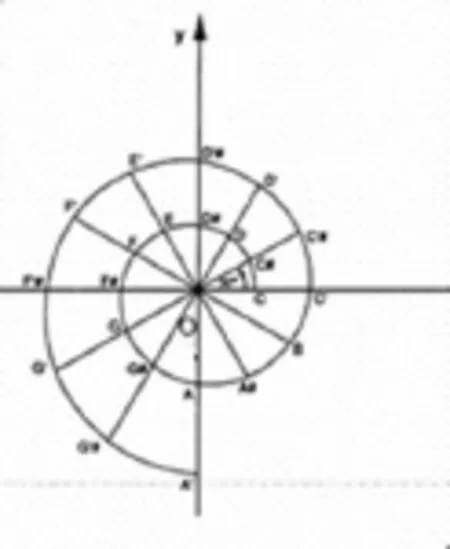
图2 对数螺旋线应用于转调

对数螺旋线有一条重要性质：作任何初等变换后其还是对数螺旋。伯努利一生酷爱对数螺旋，由此而用“我将按着原来的样子变化后复活”作为他的墓字铭，就取自于螺旋线不变性之意。

（3）乐器之王——钢琴键盘的“黑雪”（和谐）美

一个音程，从音名1到高音1的黑白键盘数及和数为2，3，5，8，13构成了斐波拉契数列，其环比暗含黄金比率。

（4）傅里叶级数

傅里叶曾预言“器乐和声乐都可用数学式来描述”，并用简单的数学式——周期正弦函数和余弦函数来表示，从而发现了三角级数。

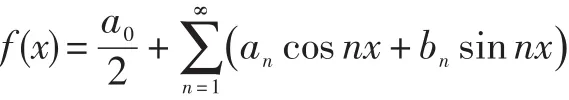
4.比尔折线

比尔是瑞士的设计师、艺术家，其影响不止于使荣汉斯（Junghans）钟表品牌设计成为世界经典，更在于其精湛光彩的作品展现的文化创意。如图3是比尔的创意折线，画法是：三角形不画第三边，接着画四边形但不画第四边，依此类推，无限画下去。图4是用其创意生产出来的工业产品，主要用于手表背面的工艺。

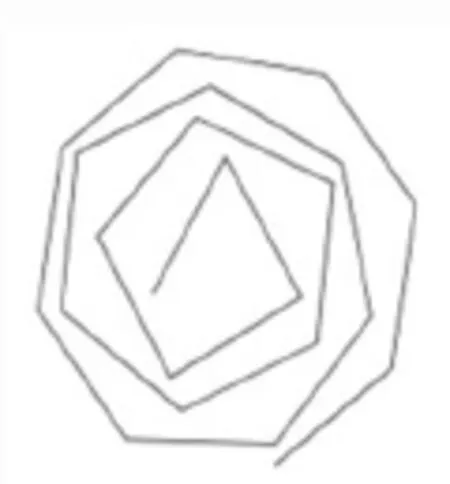
图3 比尔折线

图4 比尔的创意作品

5.曼德布劳特分形

美国物理学大师约翰·惠勒说：“今后谁不熟悉分形，谁就不能被称为科学上的文化人”。中国著名学者周海中教授认为：分形几何不仅展示了数学之美，也揭示了世界的本质，还改变了人们理解自然奥秘的方式；分形几何是真正描述大自然的几何学。对它的研究也极大地拓展了人类的认知疆域。

分形是如何发现的？数学家曼德布罗特（B.B. Mandelbrot）研究海岸线的长度时发现：许多国家的公共边界线存在极大的误差----大国公布的公共边界线小，而小国公布的公共边界线大，何故？

可以通过冯·科赫（Von Koch）曲线来进行解释。如图5，通过计算以下各线段的总长度，就不难发现：

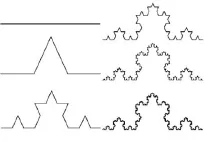
图5 冯·科赫曲线

设(l(E0)=1)，Ek是由Ek-1的每一个直线段中间1 3用等边三角形的另外两边取代而得到的。k→∞时Ek的长度

用二叉树的做法，在平面上标定出二进小数0.0，0.1，0.01，0.11，0.001，0.011，0.101，0.111，…。从而形成了H分形图。

分形之美鉴赏：分形艺术作品体现出许多传统美学的标准，如平衡、和谐、对称等等；结构丰富饱满却不杂乱；蕴涵着无穷的嵌套结构；有序和无序的和谐搭配，正是“天道崇美”的一种表现手法。

分形之哲学美：阐释了“一沙一世界”的哲学意境。

为了让学生理解分形中无限嵌套的意义，设计一道数学题让学生训练：化简无限迭代分式体味分形之美。

（二）高等数学的美育——渗美

高职高等数学一般包含《微积分》《线性代数初步》《概率统计初步》。在教学设计中要适时渗透数学之美。其主要美育形式和结点有：

1.简捷美。如极限、导数的定义和计算公式；

2.统一美。如在各类积分计算中，借助不同公式，可以将线积分、面积分、重积分、定积分，通过不断转换最终都转化为不定积分；

3.对称美。如定积分关于奇偶函数的性质，在函数图像描绘中，常见的具有对称性的心脏线、玫瑰线等漂亮曲线和马鞍面、椭球面等完美曲面；

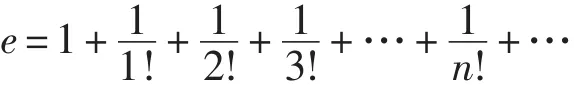
（三）专生本数学——拣美

专升本数学教学目的很明确，就是让学生考取理想的本科。结合专生本《高等数学》考试大纲和历年考点分析，就数学思想和解题方法，删繁就简，对比凸显，拣最美最易方法进行教学是最优设计，数学美主要体现在解题过程中。如：

1.简捷美。以下3道微分方程解答过程中，任意常数的取法就源自于答案简捷美的要求。

4.奇异美。如用级数表示无理数。

方程y′=y x任意常数取法ln||y=ln||x+ln||c y′=x y 12y2=12x2+12c通解y=cx y2=x2+c y′=xy ln||y=12x2+ln||cy=ce 12x2

2.平衡美。以下一道不定积分题的2种解题技巧：加减同一项、乘除同一项，体现的就是平衡对称思想。

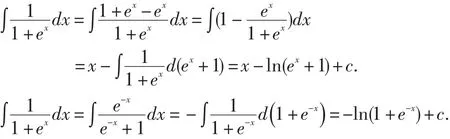
3.统一美。利用定积分的统一定义式，把复杂的极限问题转化为简单的定积分表达式，简捷明快。

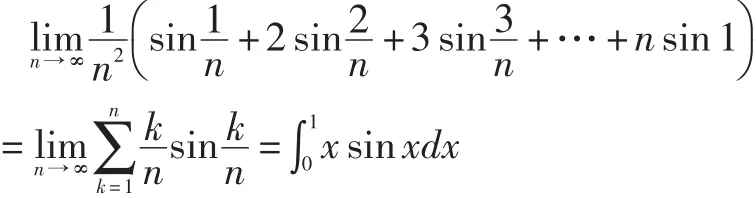
4.奇异美。有些题直接解不出来，但通过一些奇特的思维和灵异的方法，即能“化险为夷”，柳暗花明，美不胜收[4]。

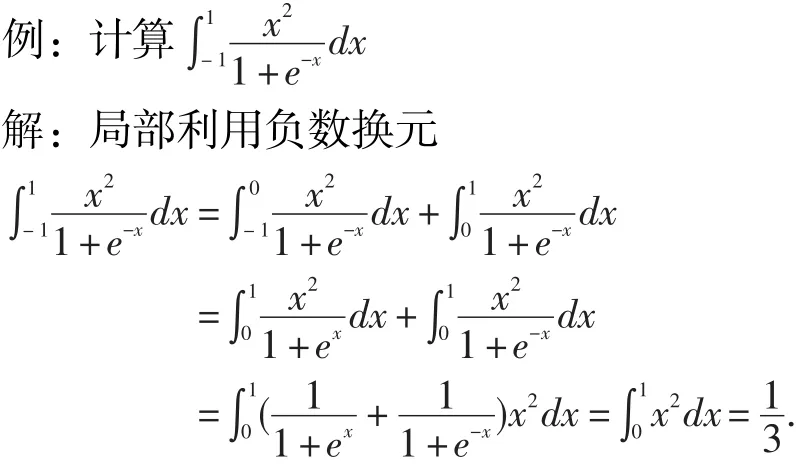
专升本解题中的数学美的呈现形式可提炼为：技巧缘于简捷（美），复杂归于简单（美），混沌清于平衡（美），奇异（美）隐于通常，深邃（美）起于猜想。

（四）数学建模——求美

数学建模是大学生四大科技竞赛之一，它能培养学生的众多能力，在高职高专也备受重视。对于不同的数学模型在解决问题效果相同前提下，追求简捷美。如人们熟知的牛顿降温模型：

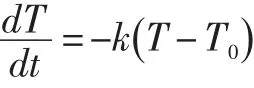
就非常简捷明了。再如，信息熵的定义式：

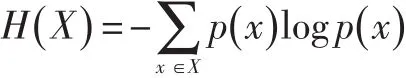
及最大熵模型：

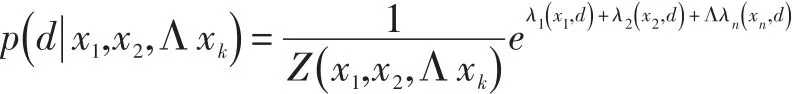
都是很优美灵性的式子。

在高职数学教学中，发掘美育的切入点，通过简捷美化复杂为简单，通过统一美化散乱为一致，通过平衡美化平庸为神奇，通过对称美化一般为特殊；通过奇异美化绝望为惊喜；通过深邃美化猜想为定理。数学课堂美育的介入，既能激发学生的学习兴趣，又能培养学生的审美鉴美能力，还能提升学生创美创新水平[5]，是一举多得的一种教学策略。

[1]干国胜,冯兴山,范光.论数学美唤起学生学习数学的兴趣[J].十堰职业技术学院学报,2009,2(1):108-109.

[2]王岳,代婷.探析高等数学中的数学美及其教学意义[J].济南职业学院学报,2013,2(1):79-81.

[3]郭培俊.科学与生活[M].北京:电子工业出版社,2015:78-91.

[4]胡桐春.数学美在高等数学解题中的运用[J].杭州师范学院学报:自然科学版,2006,11(6):503-506.

[5]宋艳丽.论高等数学中的美学思想[J].统计与管理,2016(3):191-192.

（责任编辑：尹清杰）

Dig the beauty of mathematics,expand the vision of general education

GUO Pei-jun
（Zhejiang Industry&Trade Vocational College,Wenzhou,325003,China）

In order to change the present situation of higher vocational mathematics,we put aesthetic education as a breakthrough point.The aesthetic education can be divided into four levels according to the different aspects,and the ways to design and the contents are also different:general mathematics needs abroad beauty;higher mathematics needs penetrant beauty;Top-up mathematics needs to pick beauty;and mathematical modeling need to seek beauty.Digging the elements of mathematics in higher vocational education,enriching the connotation of mathematics education,expanding the new horizons of general education,so mathematical aesthetic education is an instructional strategy to achieve multiple purpose.

Higher mathematic;Aesthetic education;General education;Hierarchical progressive

O13

C

1672-0105(2017)02-0076-04

10.3969/j.issn.1672-0105.2017.02.017

2017-02-24

2016年度高等教育教学改革项目“基于高考制度改革的高职数学文化重构”（361）；2015年浙江省教育厅一般科研项目立项课题“高职通识教育课程改革实验研究”（Y201534870）；浙江工贸职业技术学院学术委员会2016年度专项课题（XW1604）。

郭培俊，男，硕士，浙江工贸职业技术学院副教授，主要研究方向：数学建模和数学文化。