基于新阈值函数的小波分析在被动声呐消噪中的应用

赵萌 欧阳华 梁星宇 杨士雨

（1.海军工程大学电气工程学院武汉430033）（2.海军工程大学电子工程学院武汉430033）

基于新阈值函数的小波分析在被动声呐消噪中的应用

赵萌1欧阳华1梁星宇1杨士雨2

（1.海军工程大学电气工程学院武汉430033）（2.海军工程大学电子工程学院武汉430033）

论文将小波分析应用于被动声呐消噪处理中，通过对被动声呐信号的建模，提出了一种基于反双曲正切函数的阈值函数，分析了在不同阈值条件下不同阈值函数的消噪效果。仿真结果表明基于新阈值函数的小波分析消噪效果更好，能够克服传统的软、硬阈值函数消噪的不足，具有很好的应用前景。

小波分析；被动声呐；消噪；阈值函数

Class NumberTN911

1 引言

近年来，随着军事海洋环境的日益复杂，各国对海洋的开发不断深入，海军军备竞争更加激烈。声呐是各国海军进行水下监视的主要装备，其利用水中声波对水下目标进行探测、定位、跟踪、通信和导航，能有效保障舰艇、反潜机的战术机动和水中武器的使用。但在实际情况下，声呐信号往往存在大量噪声，其作战性能受到严重影响，被动声呐尤为明显。有效消噪从而获取目标信号是声呐发挥最大效用的关键。小波分析是一种多尺度信号分析方法，克服了傅立叶变换固定分辨率的特点，既可以分析信号概貌，又可以分析细节。本文主要基于小波分析研究了被动声呐的消噪问题，并提出了一种基于反双曲正切函数的阈值函数，通过仿真发现，新阈值函数在被动声呐消噪中具有较好的效果。

2 被动声呐信号模型的建立

被动声纳信号由舰船辐射噪声和海洋噪声合成。在此基础上，考虑传播过程中的能量损失，建立舰船被动声呐信号模型。

2.1 舰船辐射噪声信号

被动声纳通过接受和处理水中目标发出的辐射噪声，从而获取目标参数，舰船辐射噪声谱包括宽带连续谱分量和窄带线谱分量，其公式可表示为式中，S0(t)为连续谱时域信号，S1(t)为线谱信号。

2.1.1 被动声呐连续谱信号

根据实际测量和分析［1］，舰船噪声的连续谱在100Hz～1000Hz之间具有一个峰值，谱峰频率受舰船类型影响，频率低于谱峰频率时，频谱随频率增加略有提高；高于谱峰频率时，频谱大约以-20dB/10oct衰减。根据文献［1］，其公式可表示为

式中，SLf为f对应的噪声声压谱源级（dB）；SLS为100Hz以上的总声级（dB）；V为舰船实际航速（kn）；Vmax为舰船最高航速（kn）；DT为舰船排水量（t）。

Preliminary Study on Quantitative Research Methods of Discussion-based Teaching: CAD/CAM Course

通过得到连续谱的幅频曲线，易获得连续谱的时域信号S0(t)。

2.1.2 被动声呐线谱信号

舰船辐射噪声中线谱部分通常位于1kHz以下。引起线谱幅度变化的原因是复杂的，故线谱的幅度是一个与时间、航速、水温、海况等因素有关的多元函数。这里根据文献［2］，利用某一固定线谱幅度的数学模型：

式中，M=-200dB，A0=10-4uv，SLf为f对应的谱级分贝（dB），Rand（1）为［0，1］的随机数。Ai是第i条线谱所对应的幅值。

2.2 被动声呐传播损失

声音在传播过程中能量逐渐损失称为传播损失。这里，对于传播损失，采用球面扩展损失公式［3］：

式中，R为舰船与声呐的距离（m），a为声吸收系数，S(t)为舰船辐射噪声信号，可由式（1）得到。TL为传播损失，f为声纳工作频率。

2.3 海洋环境噪声信号

海洋环境噪声包括生物噪声、工业噪声、风浪噪声等，这种混合噪声随着时间、地点而显著变化，难以建立特定的模型。这里利用文献［4］中提供的实测环境公式：

式中，k，b为常系数，根据自然噪声平均功率谱确定，SN，j(f)是fj对应的谱级分贝（dB），基于式（4）可得到第j条线谱所对应的幅值Aj。

2.4 被动声呐染噪信号合成

综合以上分析，基于式（9）～（10），可以确定染噪信号的公式：

3 小波分析消噪

由于小波分析不同于傅立叶变换，它是一种窗口大小固定但时间窗和频率窗都可以改变的时频局部化分析方法，具有多分辨率、低熵性、去相关性等特点，用于信号消噪，取得了很好的效果，得到了广泛的应用。

对于任意的函数f(t)∈L2R，其连续小波变换定义为

式中，Ψ为基小波，a为伸缩因子且不为0，b为平移因子。

实际中，信号主要分布于低频部分，而噪声主要分布于高频部分，滤除信号的高频部分就可以消除噪声。经大量研究，人们发现噪声的小波系数和有用信号的小波系数在幅值上存在不同的表现形式，可以通过选择阈值达到消噪和保留高频信息的目的。

3.1 常用阈值函数

利用小波变换对信号进行消噪处理时，其关键问题是阈值的选取。一维小波分析消噪常用的有硬阈值和软阈值两种方法，其数学表达式分别为

由图可以看出，硬阈值函数在所取的阈值处不连续，该方法得到的小波系数对信号进行重构时会引起震荡，而软阈值函数得到的小波系数与实际信号经小波分析得到的系数存在恒定偏差，直接影响重构信号和真实信号的逼近程度。

3.2 一种新的阈值函数

针对硬阈值与软阈值方法所存在的问题，构造以下新的阈值函数：

式中，arctanh为反双曲正切函数，a，b为常系数。当a=0.2，b=1.5，T=4时，该函数曲线如图3所示。

由图3可以直观看出，新的阈值函数能够实现硬阈值、软阈值函数的同时，也克服其缺陷，便于对信号进行处理。

4 仿真验证

在四级海风的情况下，假设工作频率为1kHz的被动声呐收到了一艘在航舰船的辐射噪声，距离为2km，该舰船排水量为7000t，现时航速为20kn，最高航速为32kn，共有4条线谱，分别为0.032kHz谱级为160dB，0.255kHz谱级为154dB，0.583kHz谱级为160dB，0.723kHz谱级为163dB，海洋环境噪声有3条线谱分别为1kHz，1.782kHz，6.115kHz。

基于上文所建立的被动声纳信号模型，可对染噪信号仿真。基于航速和排水量可得到被动声纳的连续谱信号；基于线谱频谱可得到线谱信号；基于声纳的工作频率和与船的距离，可得到传播损失；基于海洋噪声线谱，可得到海洋噪声信号。染噪信号的示意图如图1所示。

我们采用信噪比来评价消噪性能。根据信噪比的定义：原始时间序列x1，x2，…，xn和消噪后时间序列y1，y2，…，yn之间的信噪比和ax-y分别为消噪后时间序列方差和噪声序列方差。信噪比越大，说明消噪信号越好。

基于文献［4］，选择dB28小波基，尺度水平为1的小波分析进行消噪。选择shannon熵类型，取阈值分别为1～20，分别在硬阈值、软阈值和新提出的阈值函数下进行消噪，得到结果如表1所示。

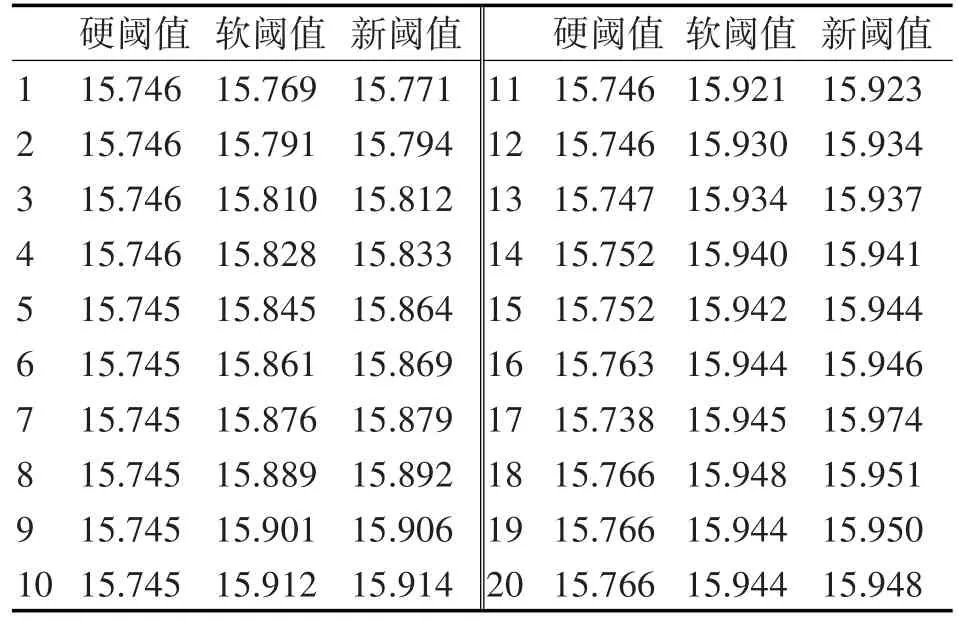
表1 不同阈值时的信噪比

由图可以发现，在相同条件下，新提出的阈值函数消噪效果更好，在阈值为17时，该阈值函数消噪效果最优。

5 结语

本文在建立了被动声呐信号模型的基础上，采用小波分析去除信号中的噪声，针对常用的软阈值和硬阈值消噪方法的不足，提出了一种新的阈值函数。既避免了硬阈值函数不连续导致的信号震荡，又避免了软阈值方法中小波系数存在的恒定偏差导致的重构信号与真实信号存在的差异的缺陷。实验结果，小波分析能较好实现消噪，新的阈值函数消噪效果最优。

［1］廖宏宇.被动声纳目标/背景建模与仿真［J］.计算机仿真，2006，23（4）：1-4.

［2］白银生，赵君渭，陈华伟.声纳数据合成仿真研究［J］.系统仿真学报，2004，16（8）：1634-1638.

［3］叶平贤，龚沈光.舰船物理场［M］.北京：兵器工业出版社，1992：23.

［4］李峰，王毅，李枚毅.基于小波的被动声呐降噪研究［J］.中国海洋平台，2007，22（5）：22-26.

［5］白志茂，黄高明，杨绿溪.基于舰船辐射噪声的舰船目标定位技术［J］.电路与系统学报，2008，13（2）：148-152.

［6］王盼盼，张国军，关凌纲.舰船辐射噪声特征线谱提取方法研究［J］.海洋技术，2010，29（3）：47-50.

［7］何风华.小波分析在信号消噪中的应用［J］.兵工自动化，2002，21（6）：22-24

［8］张建伟，张效民，相敬林.小波分析及其在水声工程中应用的探讨［J］.声学技术，1997.16（2）：94-96.

［9］王之程.舰船噪声测量与分析［M］.北京：国防工业出版社，2004：26.

［10］赵瑞珍，宋国乡.一种基于小波变换白噪声消噪方法的改进［J］.西安电子科技大学学报，2000，27（5）：619-622.

［11］Donoho D L，Johnstone I M.Adapting to unknown smoothness via wavelet shrinkage［J］.J.Amor.Star.Assoc.1995，4（90）：1200-1224.

Application of Wavelet Analysis Based on A New Threshold Function in De-nosing of the Passive Sonar

ZHAO Meng1OUYANG Hua1LIANG Xingyu1YANG Shiyu2
（1.College of Electrical Engineering，Naval University of Engineering，Wuhan430033）（2.College of Electronic Engineering，Naval University of Engineering，Wuhan430033）

In this paper，wavelet analysis is applied in de-noising of the passive sonar.A new threshold function is put forward based on the inverse hyperbolic tangent function，and the de-noising effect in different functions is analyzed with different threshold conditions.The simulation results show that wavelet analysis based on a new threshold function has better de-noising effect which can overcome the weaknesses of do-noising of the soft-threshold and hard-threshold function and has good application prospects.

wavelet analysis，passive sonar，de-nosing，threshold function

TN911

10.3969/j.issn.1672-9730.2017.06.029

2016年12月7日，

2017年1月12日

赵萌，男，研究方向：电气自动化。欧阳华，女，博士，副教授，研究方向：信号检测与处理。梁星宇，男，研究

方向：电气自动化。杨士雨，女，研究方向：无线通信。