改进QPSO算法识别结构模态参数

胡 皞，邵永亮，常 军

（1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.苏州科技大学设计研究院有限公司，江苏 苏州 215011）

改进QPSO算法识别结构模态参数

胡 皞1,2，邵永亮1，常 军1

（1.苏州科技大学 土木工程学院，江苏 苏州 215011；2.苏州科技大学设计研究院有限公司，江苏 苏州 215011）

为了进一步增强量子粒子群优化算法的全局寻优能力，提高粒子寻优效率，改善其容易陷入局部最优的缺陷，首先在引入同化和竞争思想的基础上提出一种改进的量子粒子群算法。该改进算法将民族间的同化竞争思想引入粒子寻优过程，以全局最优粒子作为中心粒子，不断同化其余粒子，使粒子之间保持不断竞争关系，以改进粒子的进化方式，提高粒子的寻优性能。接着将改进算法应用于结构模态参数识别，并采用简支梁数值模型对该算法的有效性进行验证，结果表明，改进算法较量子粒子群算法的识别精度和抗噪性都有显著的提高。最后通过三层框架试验验证改进算法在实际工程应用中的有效性。

振动与波；量子粒子群优化算法；同化与竞争；全局最优；局部最优；模态参数识别

20世纪中叶至今，伴随土木工程建设的飞速发展，一大批规模庞大、结构复杂的高层建筑、大跨度桥梁拔地而起，但是随着时间的推移，这些建筑结构在自身材料的老化、外界复杂环境的侵蚀、超负荷的运营以及自然灾害的等因素的共同影响下，都出现了不同程度的损伤、强度刚度的下降，严重影响了结构使用性能，对国家经济，人民生命财产安全产生了巨大的威胁。因此，结构健康监测逐渐受到学者们的重视，结构健康监测就是利用现代信息技术、计算机智能技术等，对工程结构进行结构检测、损伤预警，实时监控，从而保证结构的耐久性、安全性和适用性，预防和防止工程灾害的发生。结构模态参数识别作为结构健康监测的核心内容近年来也受到研究者们的广泛关注。模态参数识别的主要任务就是从所测得的振动信号中，确定结构的模态参数，包括频率、阻尼比和振型等。传统参数识别方法有极大似然法[1]、最小二乘法[2]等，但是这些传统的方法一般都是根据实验条件下的频响函数进行参数识别，这需要同时知道输入激励和响应信号，但在许多实际工程中，特别是对于一些大型结构，因无法施加激励或者施加激励费用昂贵，所以如何直接利用环境激励下的结构响应数据进行模态参数识别引起了高度重视[3–5]。

针对传统参数识别方法的不足，越来越多的研究者将智能算法引入参数识别中，提出了许多基于人工智能算法的参数识别方法，包括遗传算法[6–7]、微分演化算法[8]以及粒子群优化算法[9–11]等。2004年，针对粒子群优化算法PSO算法的缺陷，孙俊等人受到量子力学的基本理论启发，提出了量子粒子群优化(QPSO)算法[12]，同其他算法一样，其存在全局寻优能力不足且容易陷入局部最优的缺陷。针对这个问题，受到民族间同化与竞争关系的启发，本文将民族间的同化竞争思想引入QPSO算法，对QPSO算法的粒子进化方式进行改进，提出一种基于竞争的改进量子粒子群算法(以下简称ACQPSO)，进而对比改进前后算法识别结构模态参数的效果。

1 QPSO算法原理

2004年，孙俊等针对PSO算法的缺陷，提出QPSO算法[13]。在QPSO算法中，认为粒子具有量子行为，引入δ势阱，设粒子在以p点为中心的δ势阱中，因为粒子的速度和位置在量子空间中不能同时确定，故粒子的状态不再通过粒子的位置和速度来描述，而是通过粒子运动的波函数来描述

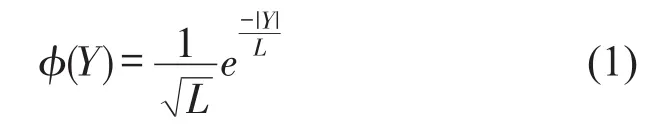
式中L为势阱δ特征长度，为粒子质量，ℏ为普朗克常数概率密度函数Q为

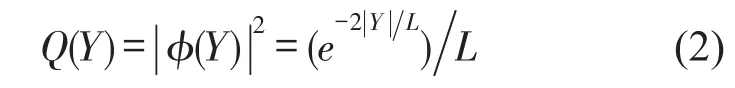
其概率分布函数F为

Q和F仅给出了粒子出现在量子空间任何位置的概率，难以准确定位，为此采用Monte Carlo方法随机模拟待测粒子的位置，得出粒子的位置方程[14]

式中u为区间(0,1)上的均匀分布随机数。

第i个吸引子第j维在t次迭代坐标表示为

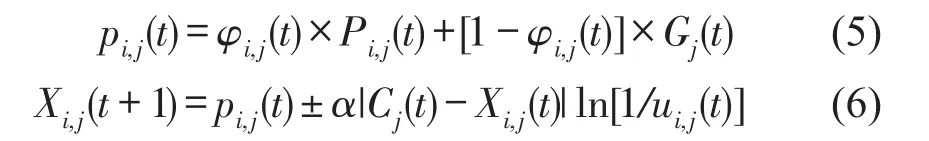
式中φi,j(t)～U(0,1)，ui,j(t)～U(0,1)，C(t)满足式(7)关系

式中Pi,j(t)，Gj(t)，Xi,j(t)和Cj(t)分别为粒子局部最优值，全局最优值，当前位置值和平均最优位置值，M为粒子群体数，参数α为压缩-扩张因子，t为粒子当前迭代次数。

每个粒子的适应值是关于位置向量的函数，适应值越小则粒子所在位置越优，每次粒子迭代更新位置后，都要计算每个粒子的适应值

2 基于竞争思想的改进QPSO算法

2.1 同化竞争思想理论

同化是民族产生以来，在社会发展各个阶段都存在的历史现象。落后的民族与先进的民族交往时，落后的民族吸收先进民族的文化，逐渐改变直到最后完全丧失自己民族的特征而变成别的民族，自然同化是先进取代落后，是历史发展的必然趋势。历史就在民族之间的不断同化斗争中得到进步发展。

本文所提出的基于竞争的量子粒子群优化算法(ACQPSO)的思想就是受到民族的同化与斗争的启发。在QPSO算法中，每一次迭代都能找到一个全局最优粒子，可以把这个全局最优粒子看成是一个最强大的民族，而其余的粒子看成是较弱的民族，全局最优粒子通过不断的同化其余粒子，使其余粒子向自己越来越靠近。从数学的角度来描述这种同化过程，通过一个随机数y来控制粒子向全局最优粒子移动的距离。定义y服从(0，ξ×d)的均匀分布

式中ξ为一大于1的同化系数，d为粒子与全局最优粒子间的距离。接下来定义粒子移动公式为

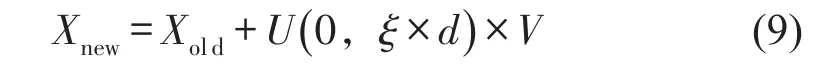
式中Xnew为同化后粒子新位置，Xold为同化前粒子位置，V为粒子到全局最优粒子的方向向量。

2.2 基于竞争的QPSO算法具体步骤

ACQPSO算法的具体步骤如下：

①确定种群规模、维数，并初始化粒子位置；

②根据公式(7)计算粒子种群的平均最优位置；

③计算每一个粒子的初始适应值，得到粒子初始最优位置和初始全局最优位置；

④根据公式(6)更新每个粒子的位置；

⑤计算每个粒子适应值，找出全局最优粒子；

⑥根据公式(9)将其余粒子进行同化，产生新的粒子种群；

⑦对同化后的粒子一一进行比较，若存在较全局最优粒子更优的粒子，则替代全局最优粒子。

⑧判断算法是否达到最大迭代次数，若没有则返回步骤④；

⑨输出全局最优位置G，算法结束。

2.3 改进算法性能分析

为了测试ACQPSO算法的性能，将采用6个常用标准测试函数，函数相关信息如表1所示，对ACQPSO算法进行测试，并与QPSO算法进行比较。在仿真测试中，采用种群规模为20，维数取10，最大迭代次数为1 000，收缩-扩张因子α的值随迭代次数从1.0到0.5线性减小，同化系数ξ=2。测试结果如表2所示，测试函数收敛曲线如图1所示：

本文所选测试函数中，Sphere函数为非线性且图像对称的单峰函数，主要用与检验算法的寻优精度；Rosenbrock、Schwefel和Ellipse函数主要用于检验算法的寻优能力；而Griewank函数和Ackley函数都为多峰函数，具有大量的局部最优点，所以算法很容易陷入局部最优，所以一般用于检验算法抵抗局部最优能力。以上述测试函数运算结果和寻优曲线来看，ACQPSO算法的识别结果大大优于QPSO算法，这表明在改进算法的粒子进化过程中加入同化和竞争处理，对提高算法寻优能力、收敛精度和防止陷入局部最优都起到非常好的效果。

3 ACQPSO识别结构模态参数

3.1 问题描述

结构的模态参数识别问题可以看作是一个优化问题，即最小化真实结构的实测响应数据和预测结构模拟数值响应数据的误差。设y(t)为k个自由度黏性阻尼系统的结构振动响应，表达式为

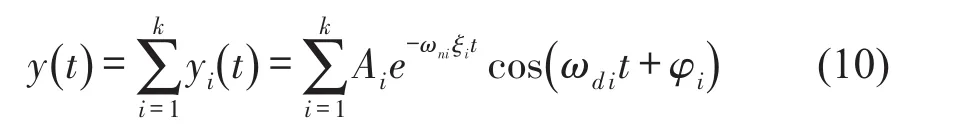
式中yi(t)表示结构振动响应输出，Ai为振动幅值，ωni、ωdi分别为无阻尼和有阻尼的结构阻尼圆频率，ζi为阻尼比，φi为相位角，t为时间变量。其中有阻尼圆频率ωdi为

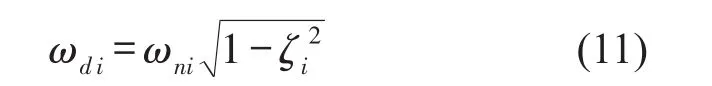
本文将采用均方误差函数

表1 测试函数基本信息

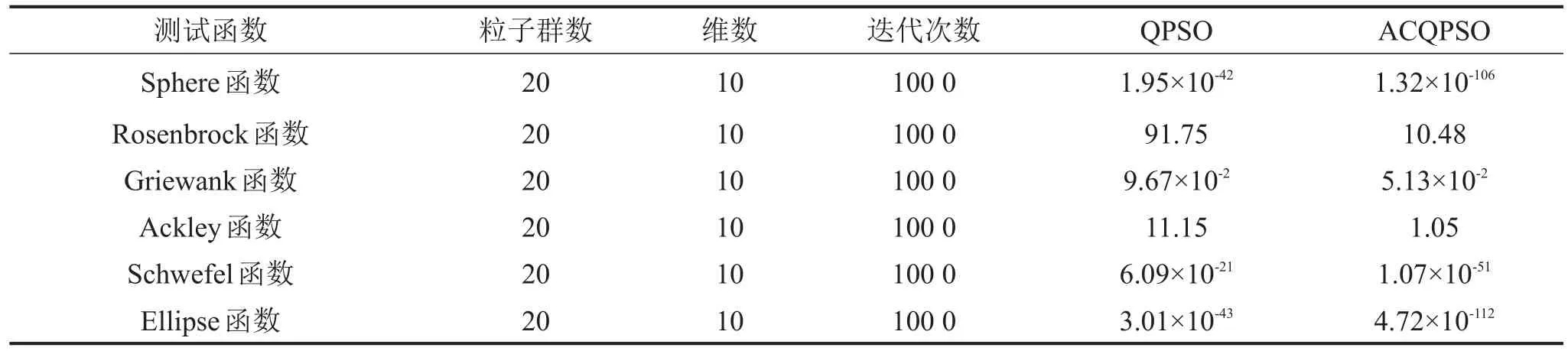
表2 测试函数的测试结果

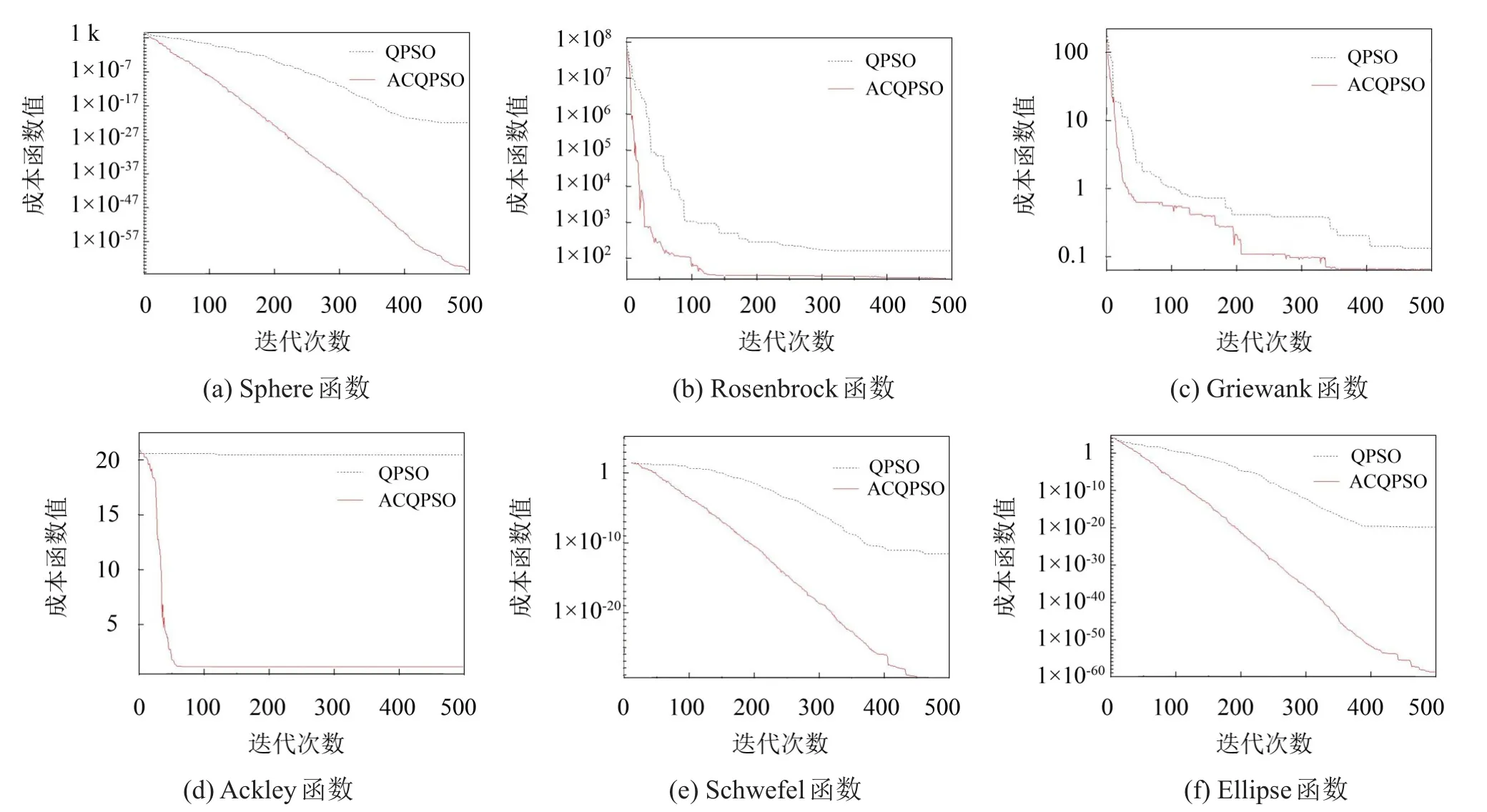
图1 测试函数寻优曲线

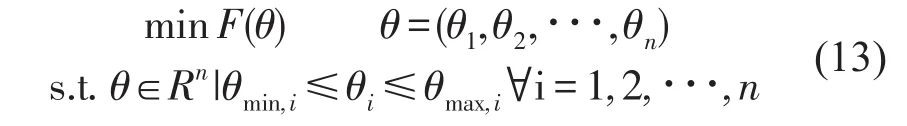
式中θmax和θmin分别为n个待识别参数取值的上限和下限，它们构成了待识别的区间范围。

3.2 数值模拟参数识别

如图2所示，建立一简支梁模型，模型采用两端简支的钢板矩形梁，截面尺寸为26 mm×10 mm，梁长为3.00 m，材料为Q235钢材。模型的惯性矩是2.167×10-9，弹性模量是2.06×105MPa，密度是7 850 kg/m2。沿梁长1/8节点处均布7个加速度传感器，并在这7个位置施加稳态白噪声激励。采样频率f= 1 000 Hz，响应信号时间50 s，阻尼按照Rayleigh阻尼，第1阶和第6阶阻尼比设为2%，其余按公式计算，加噪从0%到30%。加入峰值拾取法(PP)作对比，分别采用PP、QPSO和ACQPSO识别结构模态参数。粒子数取60，迭代次数为2 000，α的值随迭代次数从1.0到0.5线性减小，同化系数ξ=1.5。识别结果如表3－表5所示，振型图如图3所示。

图2 简支梁结构模型(单位：mm)

由上述简支梁结构模态参数识别结果可知，利用均方误差作为目标函数，并采用优化算法对目标函数进行优化，从而识别出结构的模态参数的方法是完全可行的。在频率识别上，ACQPSO算法识别效果明显优于QPSO算法、PP法；在阻尼比识别上，ACQPSO、QPSO算法的识别精度较PP法有很大提高；在振型识别上，当加噪到30%时，ACQPSO算法较QPSO和PP法存在明显优势，且从数据上来看，ACQPSO算法的抗噪性能强于QPSO算法。

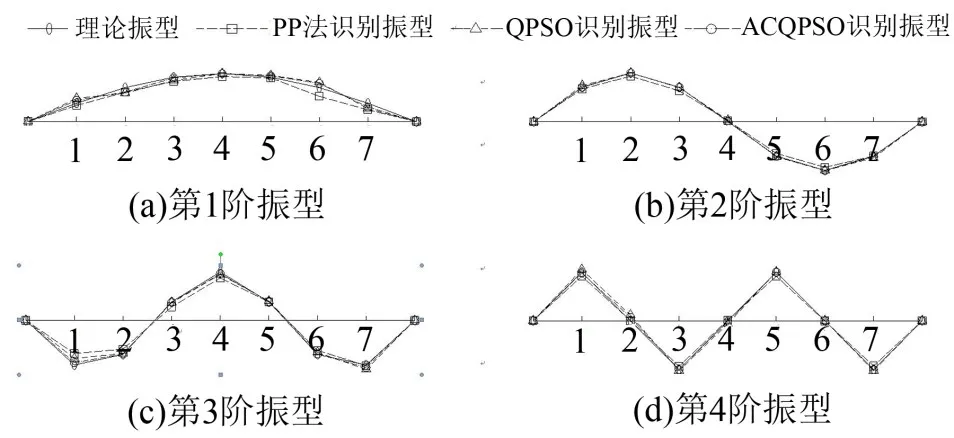
图3 简支梁振型图

3.3 结构试验参数识别

在实验室建立如图4所示的三层钢框架结构，各层布置加速度传感器，用以测量框架各层加速度响应时程，传感器采用频率为1/0.000 195，将该框架结构放置在小型振动台上进行脉冲试验，脉冲试验开始前传感器开始采集数据记为0 s时刻，第5.85 s时开始激励，第20 s结束振动。收集提取全部试验数据进行分析处理。

分别采用峰值法(PP)、QPSO算法和ACQPSO算法对试验采集到的响应数据进行处理，从而识别出该三层框架的模态参数。此次计算粒子数取60，迭代次数为3 000，α的值随迭代次数从1.0到0.5线性减小，ACQPSO算法中，同化系数ξ=1.5。识别结果如表6－表7和图5所示。

在模态参数识别中，由于PP法作为比较成熟的识别方法，且识别结果具有一定的可信度，因此，本试验参数识别采用PP法的识别结果作为参考标准，验证ACQPSO算法在实际应用中的有效性和可靠性。从试验识别结果来看，频率方面，ACQPSO与QPSO算法识别结果与PP法都较为接近；阻尼方面，由于此结构是大阻尼结构，PP法对于结构第2阶的阻尼无法识别，QPSO与ACQPSO成功识别；振型方面，通过MAC值的比较，ACQPSO的识别结果更接近于PP法。由此可以得出结论，ACQPSO在实际应用中的识别结果具有相当高的可靠性。

表3 结构固有频率识别结果

表4 结构阻尼比识别结果

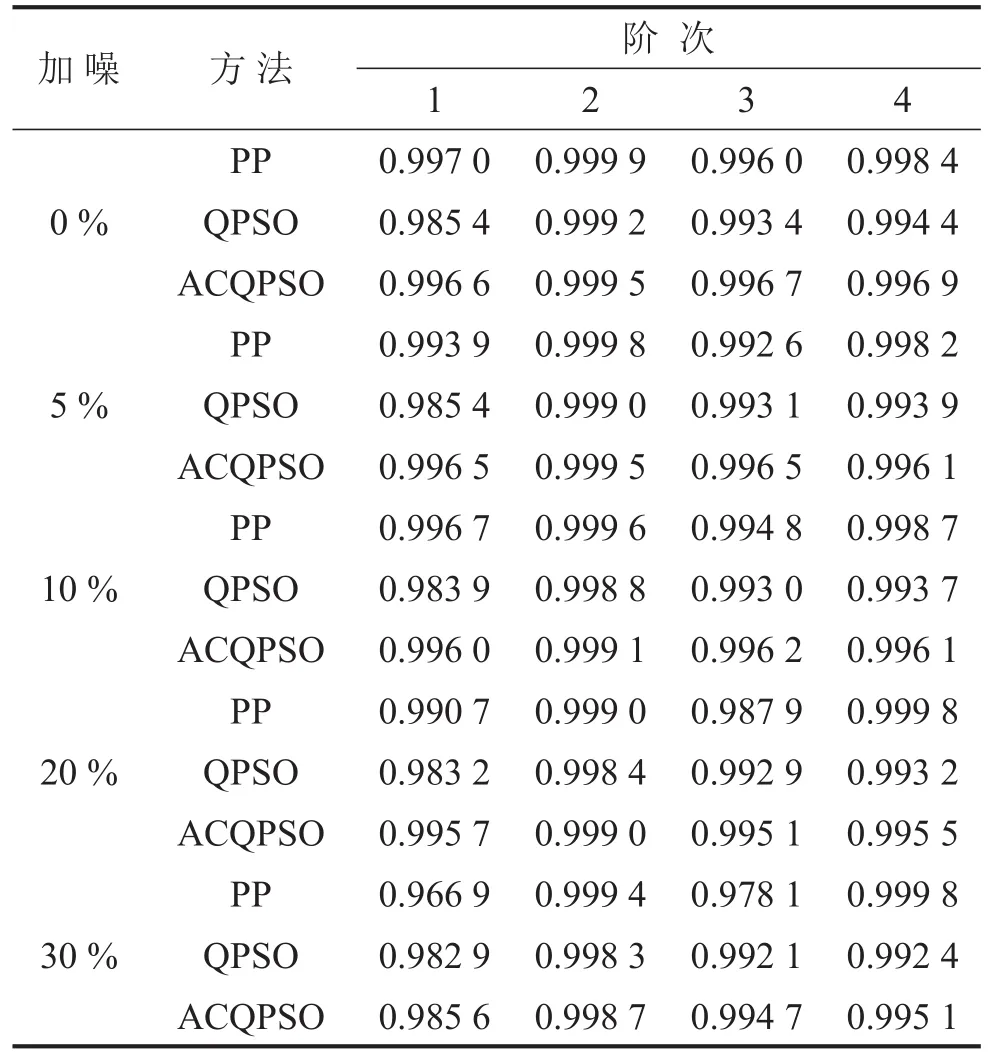
表5 结构振型MAC值识别结果

图4 三层框架结构试验图

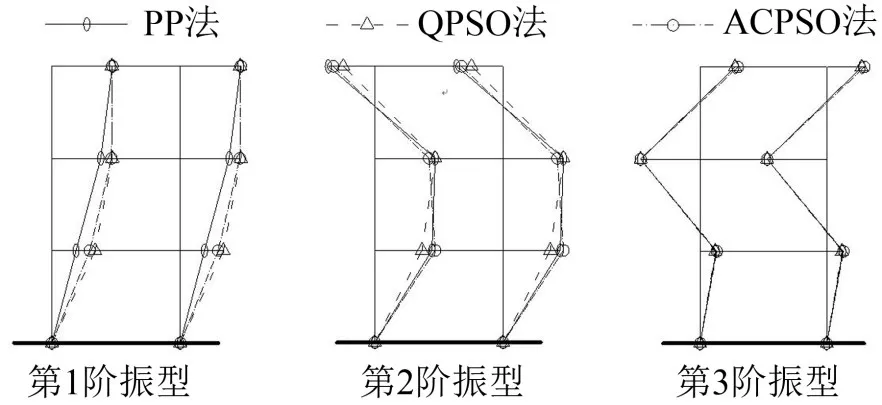
图5 三层框架试验振型图

表6 结构频率、阻尼的识别结果

表7 振型MAC值的识别结果

4 结语

针对QPSO算法全局寻优能力不强，容易陷入局部最优的缺陷，本文首先将民族间同化竞争的思想引入QPSO算法，对QPSO算法的粒子进化方式进行改进，提出了ACQPSO算法。

(1)通过典型测试函数的仿真结果分析表明，在不带来附加计算时长、不增加算法繁琐程度的情况下，ACQPSO算法的全局寻优性能和避免陷入局部最优能力都得到了很大的提高，因此基于同化与竞争的改进方法是有效的。

(2)将ACQPSO算法应用于结构模态参数识别的实际应用中，通过对一简支梁结构进行数值模拟，并与QPSO算法进行对比，识别结果表明，改进后的算法的识别精度与抗噪性均得到显著提高。对三层框架结构试验信号进行参数识别，并以PP法作为参考标准，识别结果表明ACQPSO算法识别结果与PP法更为接近，在实际工程应用中具有很高的可靠性。

(3)综上所述，改进方法ACQPSO算法是成功的，并且在实际应用中也得到了很好的验证，因此，本文提出的改进思想对于群体智能优化算法的进一步发展具有很大的指导和推动作用。

[1]CAMPILLO F,MEVEL L.Recursivemaximum likelihood estimation for structural health monitoring tangent filter implementations[C].Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference(CDC-ECC’05),Seville Spain,2005.

[2]YANG J,PAN S,LIN S.Least squares estimation with unknown excitations for damage identification of structures[J].J Eng Mech,2007,133(1):12-21.

[3]纪晓东，钱稼茹，徐龙河.模拟环境激励下结构模态参数识别试验研究[J].清华大学学报(自然科学版)，2006，46 (6)：769-772.

[4]张之颖，谭高铭，吕西林.环境激励下房屋建筑阻尼比的识别方法[J].西安建筑科技大学学报(自然科学版)， 2007，39(6)：767-772.

[5]续秀忠，华宏星，陈兆能.基于环境激励的模态参数辨识方法综述[J].振动与冲击，2002，21(3)：1-5.

[6]PERRY M J,KOH C G,CHOO Y S.Modified genetic algorithm strategy for structural identification[J].Computers&Structures,2006,84(8-9):529-540.

[7]KOH C G,HONG B,LIAW C Y.Substructural system identification by genetic algorithms[C].3rd US Japan Workshop on Nonlinear System Identification and Structural Health Monitoring,LosAngeles(CA),2000.

[8]TANG H,XUE S.Differential evolution strategy for structural system identification[J].Computerand Structures,2008,86(21 22):2004 2012.

[9]COELHO L.S.KROHLING,R.A.Nonlinear system identification based on B-spline neural network and modified particleswarm optimization[C].Vancouver, Canada,Proc.IEEE World Conference on Computational Intelligence(WCCI),2006.

[10]榎本裕里，杨晓楠.粒子群优化算法在结构参数识别中的应用[J].结构工程师，2010，26(3)：78-81.

[11]张伟.基于粒子群优化算法的结构参数及损伤识别[D].上海：同济大学，2008.

[12]SUN J,FENG B,XU W B.Particle Swarm Optimization with Particle Having Quantum Behavior[C].2004 IEEE Congress on Evolutionary Computation,Portland,OR, US:IEEE Press,2004:325-331.

[13]孙俊.量子行为粒子群优化算法研究[D].无锡：江南大学，2009.

[14]常军，巩文龙.量子粒子群结合小波变换识别结构模态参数[J].振动与冲击，2014，33(23)：42-46.

Structural Modal Parameter Identification Based on Improved QPSOAlgorithm

HU Hao1,2,SHAO Yong-liang1,CHANG Jun1
（1.School of Civil Engineering,Suzhou University of Science and Technology, Suzhou 215011,Jiangsu China; 2.Architectural Design and Research Institute of USTS,Suzhou 215011,Jiangsu China）

To further enhance the ability of quantum-behaved particle swarm optimization(QPSO)algorithm in global optimization,raise the efficiency of particles searching and overcome the defect that QPSO may fall into the local optimum easily,an improved QPSO algorithm is proposed.The idea of national assimilation and competition is introduced into the particle optimization process.In the improved QPSO,the global best particle,treated as the central particle,assimilates the other particles constantly.At the same time,competition is maintained among the particles to improve the optimization performance of the algorithm.Then,the improved QPSO is applied to the structural modal parameters identification.The results of numerical simulation of a simply supported beam show that the identification accuracy and the noise-immunity are both improved remarkably.At last,the test of a 3-story frame structure is carried out to verify the practicability and reliability of the improved QPSO.

vibration and wave;quantum-behaved particle swarm optimization algorithm;assimilation and competition;global optimum;local optimum;structural modal parameters identification

TP206+.3

：A

：10.3969/j.issn.1006-1355.2017.03.016

1006-1355(2017)03-0082-06+116

2016-12-26

江苏省自然科学基金资助项目(BK20141180)；江苏省结构工程重点实验室开放课题(DZ1405)；江苏省建设系统科技项目(2015ZD77)

胡皞(1989－)，男，江苏省苏州市人，硕士研究生，主要研究方向为桥梁健康监测。

常军，男，教授，博士，主要研究方向为桥梁健康监测与振动控制研究。E-mail:changjun21@usts.edu.cn