基座刚度对主被动隔振系统控制效果的影响分析

张 能，何 琳，李 彦

（1.海军工程大学 振动与噪声研究所，武汉 430033；2.船舶振动噪声重点实验室，武汉 430033）

基座刚度对主被动隔振系统控制效果的影响分析

张 能1，2，何 琳1，2，李 彦1，2

（1.海军工程大学 振动与噪声研究所，武汉 430033；2.船舶振动噪声重点实验室，武汉 430033）

为了研究基于弹性基座的主被动隔振系统的隔振性能，将弹性基座简化为一个大刚度弹簧连接的质量单元，建立主被动隔振系统的三自由度模型和运动方程，推导主通道传递函数和次级通道传递函数的频域表达式。结合Fx LMS自适应控制算法，在Matlab/Simulink中建立该隔振系统模型，对上层机械设备施加含白噪声的多频正弦激励力，进行主动隔振研究。分析基座刚度对主通道、次级通道传递函数的幅频特性，振动线谱控制效果以及主动控制力的影响。结果发现较大的基座刚度有利于提高振动线谱控制效果，也有利于降低主动控制力需求。

振动与波；弹性基座；主被动隔振；Fx LMS算法；振动线谱控制；幅频特性

传统的刚性基座假设是，将基础看作是具有无限质量的绝对刚性体，所有运动参量为零。在舰船的隔振系统中，基座是有一定弹性的[1]，其质量也不是无限大的，基座刚度对隔振系统的性能会产生重要影响[2]。

主被动隔振技术是通过被动装置承载设备重量并隔离宽频振动，作动器对振动线谱进行主动控制[3–4]。部分学者对柔性基础的主被动隔振技术开展了研究[5–7]，采用梁或者板的结构来模拟基座，分析了主动隔振系统的阻抗/导纳、功率流传递特性等[8–9]。由于以梁、板结构来模拟基座，需要基座三维尺度满足一定的假设条件，而且梁、板结构的导纳矩阵相对复杂，分析结果难以推广到一般弹性基座的隔振系统研究中。本文提出将基座简化为一个大刚度弹簧连接的质量单元，这样可以给动力学建模与分析带来便利，也能揭示弹性基座的普遍规律。

针对基座刚度对主被动隔振系统性能的影响这一问题，本文建立了基于弹性基座的三自由度主被动隔振系统的运动方程，通过拉普拉斯变换求得了主通道和次级通道的传递函数。采用FxLMS自适应前馈控制算法，在Matlab/Simulink建立了该隔振系统的仿真模型。在含白噪声的多频正弦作用力激励下进行振动线谱控制研究，分析了基座刚度对主通道、次级通道传递函数的幅频特性，振动线谱控制效果以及主动控制力的影响。

1 理论研究

1.1 弹性基座主被动隔振系统运动方程

如图1所示为某型主被动隔振系统的结构示意图，m1、m2和m3表示机械设备、中间筏架和基座，基座与中间筏架之间由被动隔振器和作动器并联，基座与参考系弹性连接。

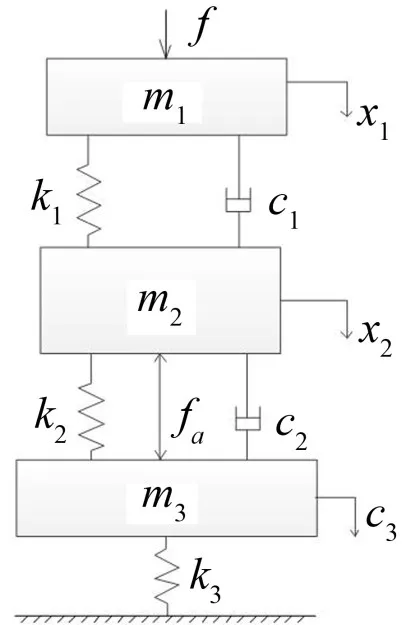
图1 主被动隔振系统结构示意图

在如图1所示弹性基座主被动隔振系统中，主动隔振的基本原理是：采集机械设备所受的激励力信号，输入控制器中，控制器基于自适应前馈控制算法产生驱动电流信号，经过功率放大器及作动器后，输出主动作用力作用于筏架和基座，抑制传递至基座的振动，控制的目标是最大程度减小基座的振动。

针对此系统，建立三自由度运动方程

式(1)中，f为激励力，fa为主动控制力，其他特征参数及其参数值如表1所示。

表1 系统模型参数

1.2 主通道、次级通道传递函数

激励力到基座加速度的传递函数称为主通道传递函数，主动控制力到基座加速度的传递函数称为次级通道传递函数。为求得主通道、次级通道传递函数在频域的表达式。在零初始条件下，xi=ẋi=0，i=1、2、3。对式(1)进行拉普拉斯变换可得

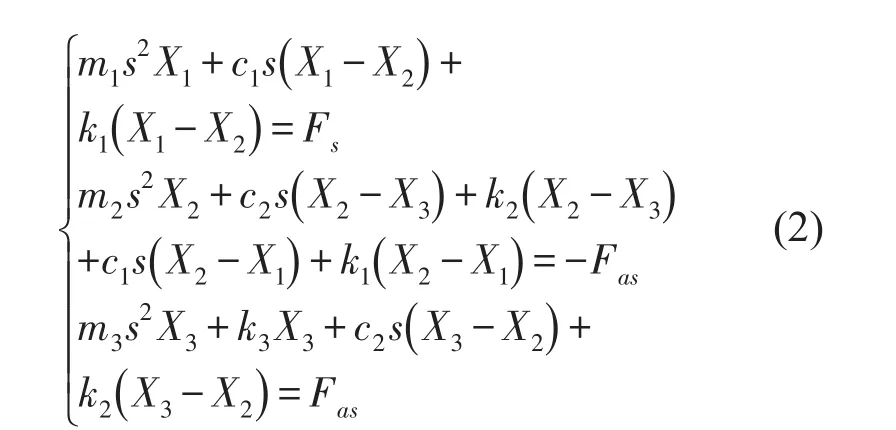
可令a=m1s2+c1s+k1,b=-c1s-k1,c=m2s2+c1s+c2s+k1+k2,d=-c2s-k2,e=m3s2+c2s+k2+k3。

由式(2)可得

分别令Fs=0、Fas=0，可得主通道、次级通道传递函数的频域表达式为

其中X3/Fs为主通道传递函数，X3/Fas为次级通道传递函数。

2 主被动隔振系统仿真模型

在第一节推导的主被动隔振系统运动方程的基础上，结合Fx LMS算法对振动线谱进行自适应前馈控制，本节建立该系统的仿真模型，模型如图2所示。

FxLMS算法通过自编的S函数模块实现，滤波器阶数为300阶，为了满足FxLMS算法的收敛条件[10–11]，滤波器权系数更新步长为0.000 2，由于滤波器阶数较高，滤波器的系数输出模块采用子系统Subsystem封装。仿真时间为10 s，求解器采用固定步长的Euler算法，步长为0.000 1 s。

3 结果与讨论

在主被动隔振系统中，为了考虑系统不可避免地受到外界干扰，选取了25 Hz、50 Hz和75 Hz倍频关系组合的正弦信号和白噪声信号叠加作为扰动激励力，其表达式为

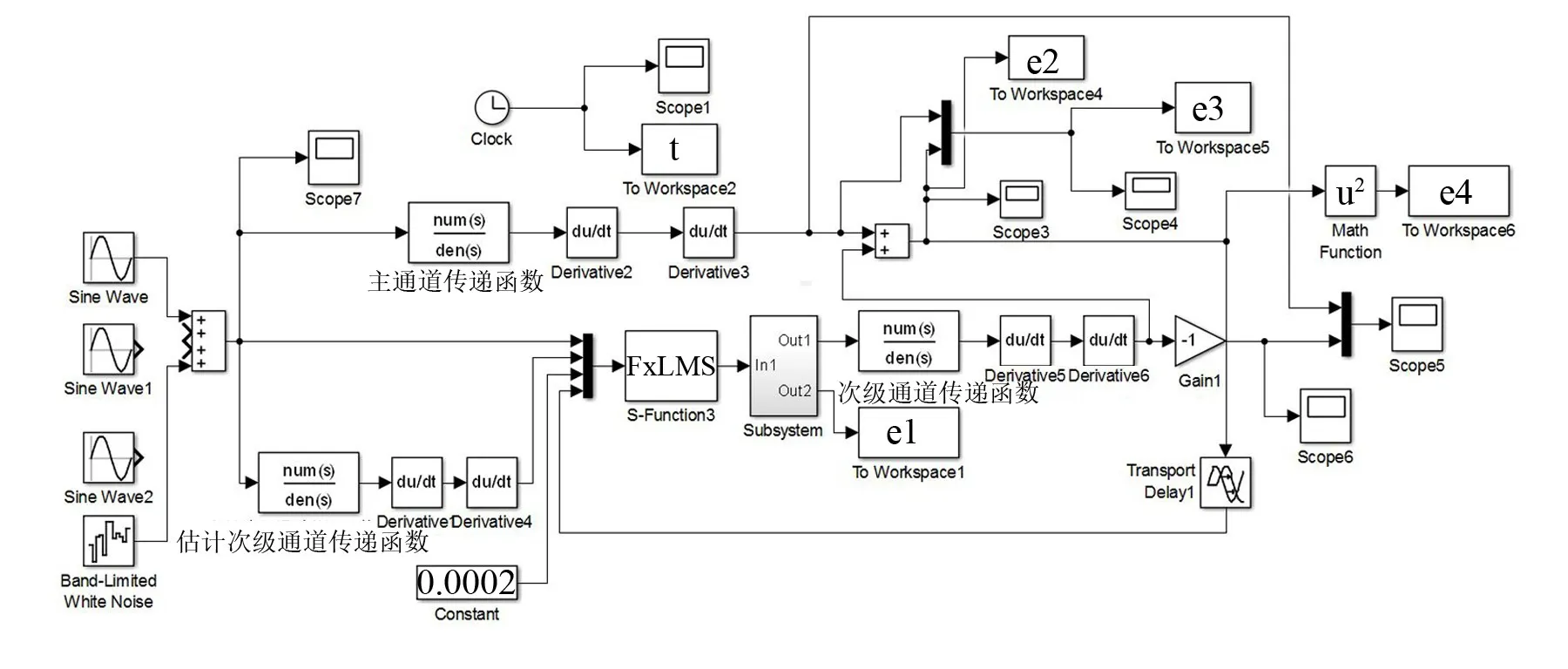
图2 主被动隔振系统Simulink仿真模型

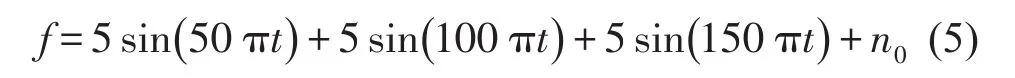
式(5)中n0为有限带宽白噪声，其噪声功率大小为0.000 2。

在下层弹簧和中层弹簧刚度比k3/k2分别为1、5、10时，分别分析了主通道、次级通道传递函数的频响特性，并对主被动隔振系统进行仿真，对比分析了振动线谱控制效果以及控制过程中主动控制力的变化情况。

3.1 幅频特性

如图3所示，随着基座刚度的增大，主通道传递函数的频响曲线第一峰值逐渐降低，对应频率缓慢增大，而第二峰值几乎不变，对应频率逐渐增大。

如图4所示，当k3/k2=1时，次级通道传递函数的频响曲线在8 Hz处存在两个比较靠近的峰，其幅值较小；随着基座刚度的增大，次级通道传递函数幅频响应曲线呈现出单个逐渐陡峭的峰值，其对应的频率逐渐增大，幅值迅速增大。

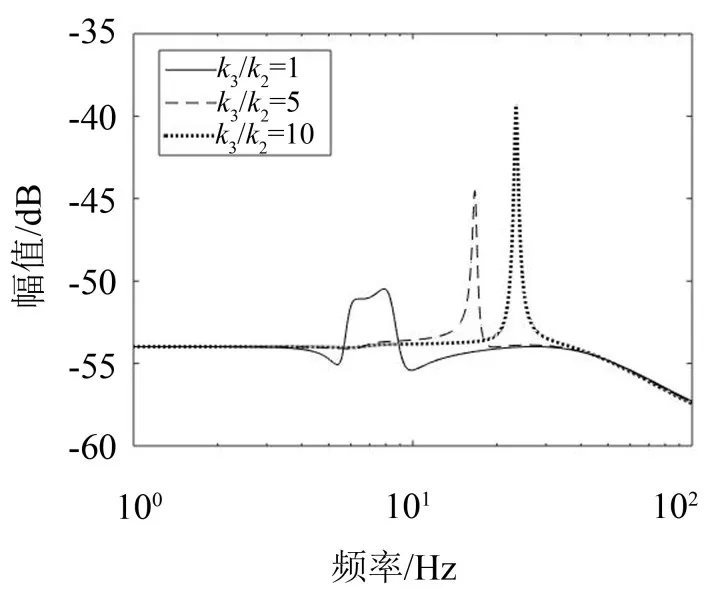
图4 次级通道传递函数幅频响应曲线

3.2 线谱控制效果

取基座的加速度作为控制效果的评价指标，在不同的基座刚度下，控制前后基座的加速度功率谱如图5所示，25 Hz、50 Hz和75 Hz振动线谱衰减量如表2所示。

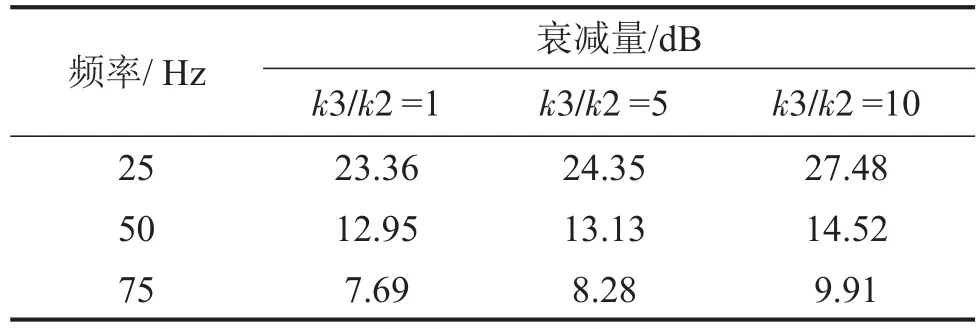
表2 振动线谱衰减量

由表2和图5可知，在k3/k2分别为1、5、10时，振动线谱都能取得一定的控制效果。

其中，25 Hz线谱控制效果最好，在三种基座刚度下都能达到20 dB以上，50 Hz和75 Hz则次之，振动线谱衰减量在10 dB左右。此外可以发现，随着基座刚度的增大，25 Hz、50 Hz和75 Hz处的振动线谱衰减量都逐渐增大，控制效果逐渐增强。

3.3 主动控制力

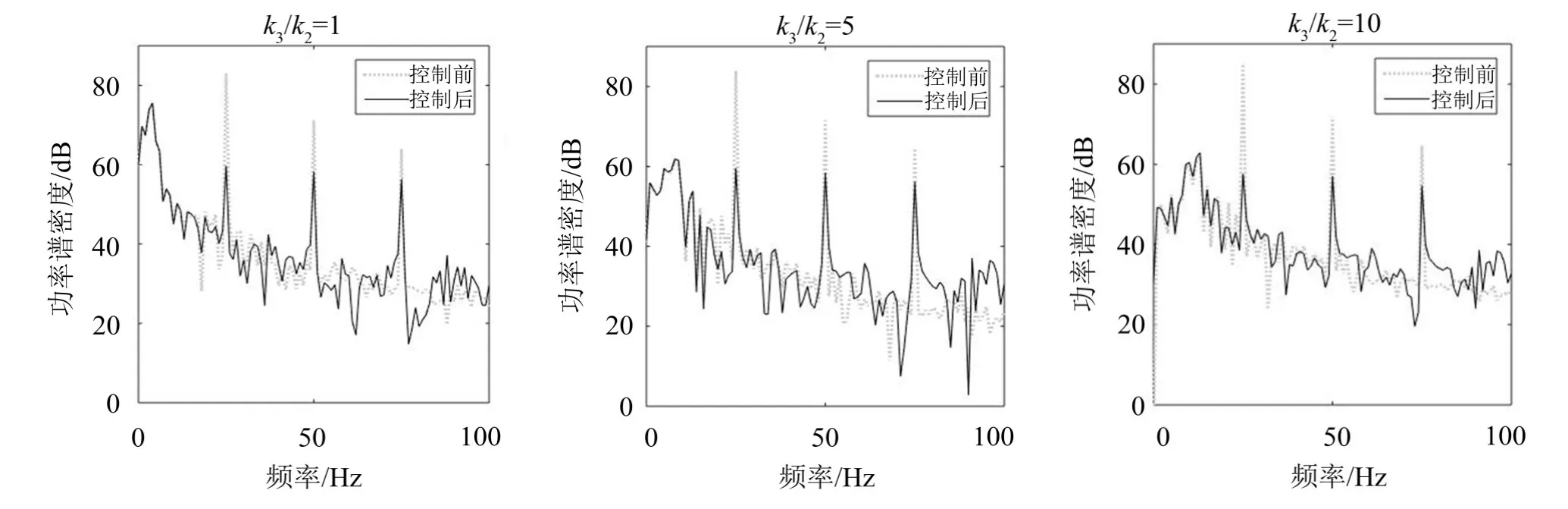
图5 振动线谱控制效果图

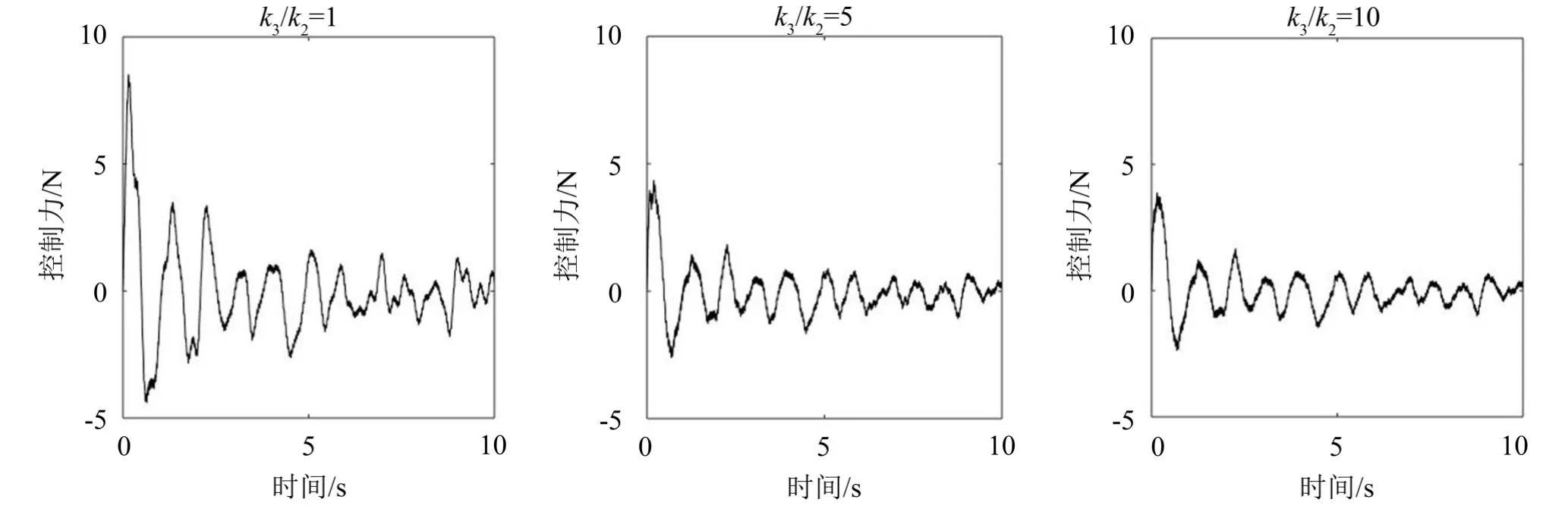
图6 主动控制力时间历程图

控制力需求也是主被动隔振系统的重要考察指标，在不同的基座刚度下，分析主动控制过程中主动控制力的时间历程变化情况，结果如图6所示。

由图6可知，在控制初期控制力非常大，在k3/k2分别为1、5、10时，最大的控制力分别为8.53 N、4.37 N和3.88 N，可见随着基座刚度的增大，最大的控制力需求逐渐降低。此外还发现，控制力在控制初期过后慢慢趋于稳定的小幅波动，这是因为激励力包含白噪声所致。

4 结语

本文建立了基于弹性基座的主被动隔振系统的动力学方程，推导了主通道和次级通道的传递函数模型，采用Fx LMS算法，在Matlab/Simulink中对主被动隔振系统开展线谱控制仿真研究，在不同的基座刚度下，分别分析了基座刚度对主通道、次级通道传递函数的幅频特性，振动线谱控制效果以及主动控制力的影响。结果发现随着基座刚度的增大，控制效果增强，所需的最大主动控制力降低，增大基座刚度对提高主被动隔振系统隔振性能，降低控制力需求具有重要作用。

[1]朱石坚，楼京俊，何其伟，等.振动理论与隔振技术[M].北京：国防工业出版社，2006.

[2]管延峰.柔性基础多支承非线性隔振系统动力学分析[D].济南：山东大学，2013.

[3]李彦，何琳，帅长庚，等.磁悬浮主被动隔振系统的自适应控制和非线性补偿[J].振动与冲击，2015，34(6)：89-94.

[4]何琳，李彦，杨军.磁悬浮-气囊主被动混合隔振装置理论和实验[J].声学学报，2013，38(2)：241-249.

[5]徐洋，孙以泽，华宏星，等.主动柔性耦合隔振系统的直接速度反馈实验研究[J].振动与冲击，2009，28(4)：6-8.

[6]袁万朋.弹性基础上的主动隔振技术研究[D].哈尔滨：哈尔滨工程大学，2012.

[7]徐洋，华宏星，张志谊.舰用主动柔性耦合隔振系统建模研究[J].工程力学，2008，25(12)：223-228.

[8]徐洋，孙志军，陈广峰，等.柔性耦合隔振系统主动控制方法的仿真研究[J].噪声与振动控制，2010，30(2)：16-18.

[9]承颖瑶.柔性隔振系统的功率流传递特性与控制研究[D].上海：上海交通大学，2009.

[10]FULLER C R,ELLIOTT S J,NELSON P A.Active control of vibration[M].London:Academic Press,1997.

[11]范威.主动隔振器及自适应控制方法研究[D].上海：上海交通大学，2008.

Analysis of the Effect of Base Stiffness on Control Performance of Passive-active Vibration Isolation Systems

ZHANG Neng1，2,HE Lin1，2,LI Yan1，2
（1.Institute of Noise and Vibration,Naval University of Engineering,Wuhan 430033,China; 2.National Key Laboratory on Ship Vibration and Noise,Wuhan 430033,China）

The isolation performance of the passive-active vibration isolation system on a flexible base is investigated. The flexible base is simplified as a mass element connected to a spring with large stiffness.The 3-DOF model of the passiveactive vibration isolation system on the flexible base is established and the corresponding dynamic equation is developed. The transfer functions of primary path and secondary path are derived in the frequency domain.Combined with FxLMS adaptive algorithm,the model of the vibration isolation system is built by means of Matlab/Simulink software.The multifrequency sinusoidal exciting force containing white noise is added to the system for active vibration isolation analysis. Influences of the base stiffness on the amplitude-frequency characteristics of the transfer functions of the primary and secondary paths,vibrational spectral line control performance and active control force are analyzed.It is found that large base stiffness is beneficial for improving vibrational spectral line control performance and reducing active control force demand.

vibration and wave;flexible base;passive-active vibration isolation;FxLMS algorithm;vibrational spectral line control;amplitude-frequency characteristic

O328；TB123

A

：10.3969/j.issn.1006-1355.2017.03.012

1006-1355(2017)03-0062-04

2017-01-18

张能(1991－)，男，武汉市人，博士生，主要研究方向为振动与噪声控制。E-mail:zn710119@163.com

何琳(1957－)，男，教授，博士生导师。E-mail:helin202@vip.sina.com