结合PSO与序列运算理论的微电网的优化配置

夏惠，杨秀，杨帆，刘文飞，张春丽

（1.上海电力学院电气工程学院，上海 200082；2.国网上海市电力公司浦东供电公司，上海 200120）

结合PSO与序列运算理论的微电网的优化配置

夏惠1，杨秀1，杨帆1，刘文飞1，张春丽2

（1.上海电力学院电气工程学院，上海 200082；2.国网上海市电力公司浦东供电公司，上海 200120）

考虑到独立微电网优化配置中风光出力的随机性和负荷的波动性，建立以综合经济成本为优化目标函数的机会约束规划模型，满足供电可靠性、能量过剩率等约束条件；应用序列运算理论将随机变量离散为概率序列，将概率序列与粒子群算法中的粒子相结合表示出每时刻风光共同出力和等效负荷的概率序列，从而将机会约束规划转变为确定性计算优化求解微源的安装数量。此方法使得优化配置结果更为精确具体，并且避免了传统模拟法的耗时和每次求解结果不相同的缺点。

微网；优化配置；机会约束规划；序列运算

随着传统能源危机和环境问题的不断紧张，发展可再生能源发电技术成为解决传统能源所带来问题的必然途经[1]。分布式可再生能源的微电网技术是目前采用的重要形式，但是风光等分布式能源输出的随机性和间歇性的特点给微电网运行的安全性和稳定性带来直接影响[21-22]。

根据所需规划微网所在地的历史风速、光照强度和负荷等数据对系统进行仿真计算得到系统全寿命周期内优化目标值。但是风速和光照强度具有随机性和间歇性并且负荷也存在波动性[2]，若在规划时不考虑这些不确定性因素，则优化配置结果不能保证在实际运行状态下风光有一定程度波动时系统实际运行的安全性和可靠性的水平[3]。文献[4]提出了等可信容量概念，通过蒙特卡罗法得到风光储机组组合，从集合中选出最适合目标函数的风光储容量配置。文献[5]建立了考虑负荷波动的最优切负荷模型和综合经济成本双目标函数。文献[6]在蒙特卡罗方法的基础上，提出了多区间划分和建立概率分布从而减少了抽样次数并且简化了计算过程。文献[7]运用多状态理论对典型日的各个时刻风光出力建立了多种状态，从而全面分析了系统运行状态的所有可能性。

本文考虑到独立微网内风机出力、光伏出力和负荷的不确定性，建立了基于机会约束规划的微网优化配置模型。根据序列基本理论将风机出力、光伏出力和负荷离散化生成概率性序列，将单台风机出力和单个光伏模块出力的概率性序列与粒子群算法中的每一次迭代的粒子通过卷积运算生成每时刻风光共同随机出力和等效负荷概率性序列，将机会约束规划转化为直接性的概率计算。以具体微网系统为例，对比不同可靠性水平和离散化步长等因素对微网优化配置的影响，验证了本文方法的有效性。

1 发电单元的数学模型

本文重点研究考虑风光出力的随机性和负荷的波动性的独立微电网的优化配置，因此其他模型不作详细介绍和讨论。微网优化配置中的风速模型和风机出力模型见文献[8-9]；光照强度模型和光伏出力模型见文献[10-11]；蓄电池模型见文献[12]；负荷波动认为服从正态分布。本文所指负荷默认为有功负荷。

2 机会约束规划的优化配置模型

2.1 目标函数

独立型的微电网系统优化目标是在保证满足约束条件的前提下尽可能地减少综合成本[13]。本文以风机个数NWT，光伏个数NPV和蓄电池个数NBAT为变量，目标函数主要考虑了设备投资成本、运行和维护成本、惩罚成本及发电补贴这4部分费用。本文假设在同一地点的风机出力和光伏出力都是相同并且相互独立的。

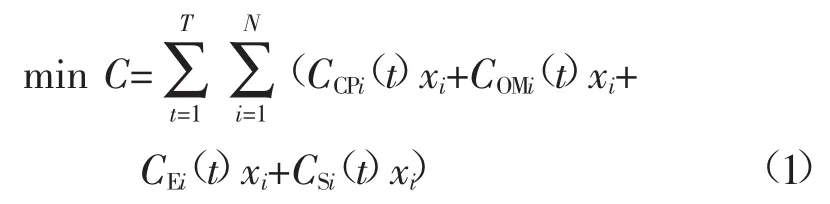
式中：T为运行时间；N为电源的类型数目；x=[x1，x2，…，xN]为决策变量，xi为第i种电源的数目；CCPi（t）、COMi（t）、COMi（t）、CEi（t）、CSi（t）分别为t时刻第i种电源的设备投资成本、运行和维护成本、惩罚成本和发电补贴。

1）设备投资费用

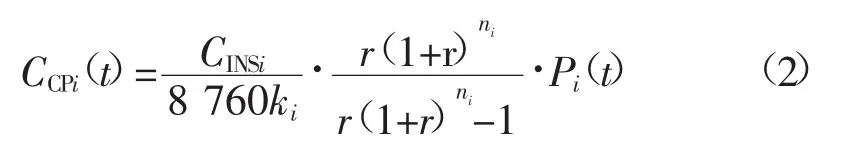
式中：CCPi是第i个微源每单位容量的投资成本；ki等于第i个微源的年发电量/（8 760×该微源的额定容量），是第i个微源的容量因数，；r为年利率，取6.7%；ni是第i个微源的寿命；Pi（t）是第i个微源在t时刻的有功输出。

2）运行和维护费用

COMi正比于微源的实际运行功率[13]：

式中：KOMi是第i个微源的每单位容量的运行维护成本系数。

3）惩罚费用

停电惩罚费CE1（t）和能量浪费惩罚费CEw（t）的引入可以减少微源总出力高于负荷需求造成的能量浪费和微源总出力低于负荷需求造成的电力不足。

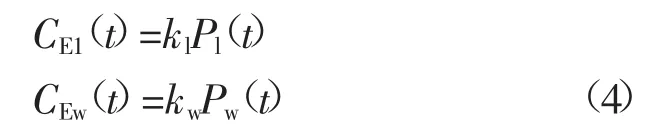
式中：kl、kw分别为能量浪费的惩罚系数和电力不足的惩罚系数；Pl（t）、Pw（t）分别为t时刻功率缺额和功率过剩。

4）发电补贴

政府对新能源发电有相应的发电补贴。

式中：ps为补贴电价；Ps（t）为t时刻风机和光伏输出功率。

2.2 约束条件

为方便理解本文定义等效负荷（equivalent Load，EL）为风机出力、光伏出力和负荷的等效值，三者的关系为[14]

1）风机、光伏出力约束

式中：PWTN、PPVN分别为单台风机和单个光伏组件的额定功率。

2）负载供电率机会约束模型

如果满足系统所有情况下的可靠性，其中包括实际运行中某些发生概率很小的极端情况，则需要很大的储能容量和较高的经济成本才能实现。运用机会约束规划方法构建负载供电率可靠性概率约束模型，即风光出力与储能容量满足负荷需求的概率。负载供电率概率约束描述如式（8），即t时刻当等效负荷小于0，则表示风光出力满足负荷需求；或者等效负荷大于0，表示风光出力不满足负荷但是此时储能剩余容量满足剩余负荷。

式中：Pr{}为事件成立的概率；α为预先给定的置信水平；R（t）为时段t内系统储能容量。

3）能量过剩率机会约束模型

能量过剩率概率约束描述见式（9），即风光出力满足负荷需求的同时又超出储能的剩余储能容量：

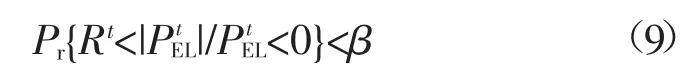
式中：Pr{}为事件成立的概率；β为预先给定的置信水平；R（t）为时段t内系统储能容量。

4）蓄电池充放电约束

①荷电状态约束

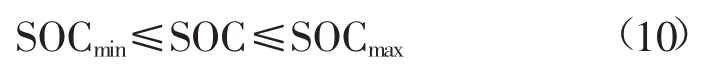
式中：SOCmin、SOCmax分别为允许荷电状态的上下限。②充放电功率的约束[15]

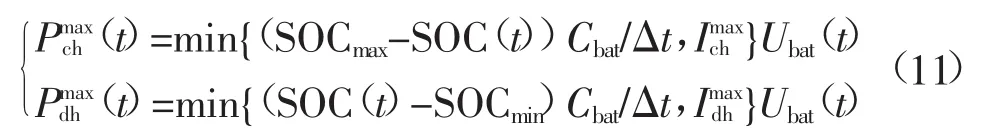
3 结合PSO与序列运算理论定量化机会约束概率

3.1 风光负荷的序列化建模

根据序列运算的基础理论将随机变量依据其概率密度函数离散为概率性序列。已知随机变量的概率密度函数为f（p），则概率性序列可表示为[16]

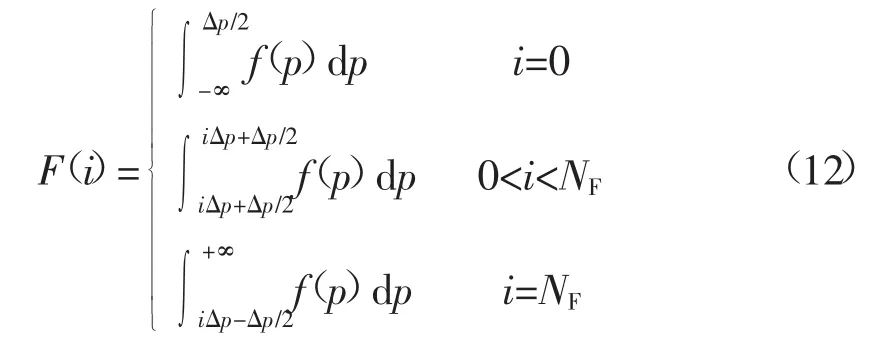
式中：NF为序列长度，取为[pmax/Δp]，pmax为随机变量最大值；Δp一般取多个随机变量的公约数，为离散化步长。

根据公式（12）将单台风机出力，单个光伏模块出力和负荷的概率分布离散化为概率性序列。如图1、2、3分别为单台风机出力、单个光伏出力和负荷的概率密度以及相应的离散化的概率性序列。

图1中单台风力发电机容量为300 W，风速概率的分布形状系数k=2.181 9，c=9.143 6；图2中单个光伏电池模块组件的容量为300 W，Beta分布的形状参数δ=4.2。图3中，负荷的期望值为25 kW，最大值为30 kW，负荷波动的标准差δL取负荷期望值UL的5%。

图1 单台风机出力的概率序列Fig.1 Probability sequence of the single wind turbine output

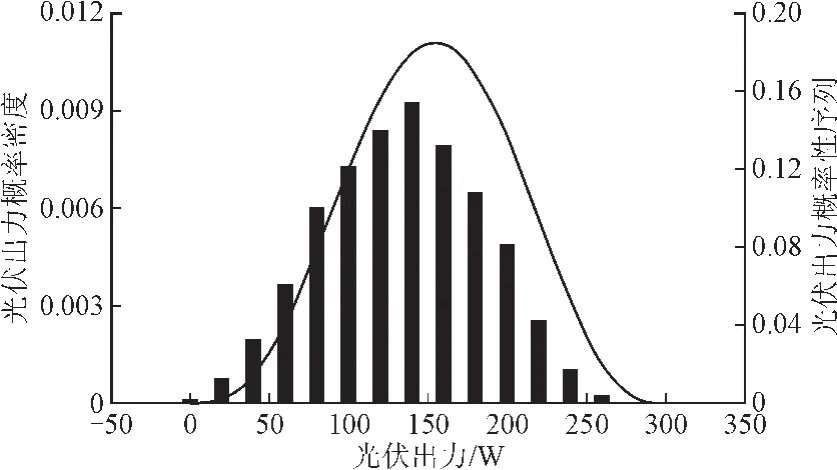
图2 单个光伏电池模块组件的概率序列Fig.2 Probability sequence of the single PV module assembly

图3 负荷的概率序列Fig.3 Load probability sequence

3.2 结合PSO与序列理论求解等效负荷的概率性序列

3.2.1 风光共同随机出力概率序列

如果t时刻风机出力PWTt和光伏出力PPVt的概率性序列分别为a（iat）、b（ibt），序列长度分别为Nat、Nbt，假设共同随机出力PWTPVt概率性序列为c（ict），序列长度为Nct，那么c（ict）由a（iat）与b（ibt）卷和运算得到：c（ict）= a（iat）⊕b（ibt），Nct=Nat+Nbt。根据卷和定义有[17]

式中，ict=0，1，…，Nct。

粒子群算法在初始化时会随机抽取粒子群，在每一次迭代过程中会改变粒子的速度和位置重新寻找最优解。本文的求解过程中每一个粒子的维数是风机个数NWT，光伏个数NPV和蓄电池个数NBAT，n个粒子则组成粒子群。

式（6）中，t时段风机出力PPVt和光伏发电PPVt的概率性序列都是数台风机的总出力和数个光伏的总出力。将粒子群算法中每一次迭代过程中的粒子取值中风机和光伏模块数量分别与时t段单台风机出力和单个光伏组件出力的概率性序列相结合，则可以得到t时段风机总出力和光伏总出力的概率性序列，经过卷和运算可得到风光共同随机出力的概率性序列。如图4是粒子中NWT=70时与单台风机出力结合的概率序列，图5是粒子中NPV=80时与单个光伏出力结合的概率序列，图6是粒子取值NWT=70、NPV=80时风光共同随机出力概率序列。

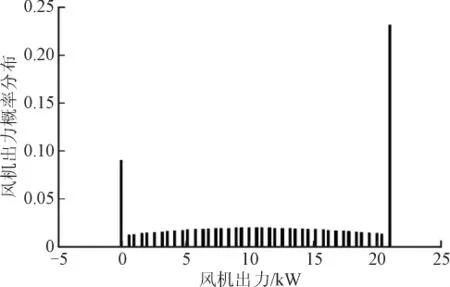
图4 粒子风机取值与单台风机出力结合的概率序列Fig.4 The probability sequence of combining the value of particle fan with the single wind turbine output

图5 粒子光伏取值与单个光伏出力结合的概率序列Fig.5 The probability sequence of combining the value of particle photovoltaic with the single PV output

3.2.2 等效负荷的概率序列

负荷概率性序列和共同随机出力概率性序列通过卷差计算可得出等效负荷的概率性序列。如果t时刻的负荷PL（t）概率性序列为d（idt），序列长度为Ndt，等效负荷PEL（t）的概率性序列为f（ift），序列长度为Nft，则由卷差计算f（ift）=d（idt）-c（ict），Nft=Ndt，等效负荷PEL（t）的概率性序列表示为

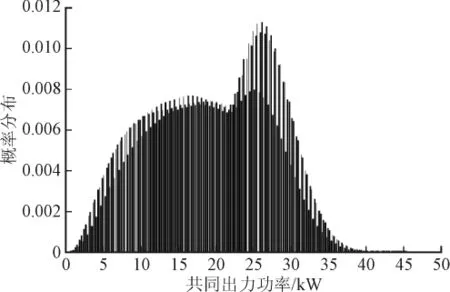
图6 与粒子结合的风光共同随机出力概率序列Fig.6 The probability sequence of combining the value of particle with the common random output

当ift=0时卷差运算是有实际物理意义的，ift=0的概率是所有负荷小于等于风光共同随机出力的概率之和，也就是将所有负荷与风光共同随机出力之差的负值部分合并到此点上，此时等效负荷小于0，可靠性满足的概率为100%，符合ift=0的实际分析需求。如图7是等效负荷的概率性序列。

图7 等效负荷的概率序列Fig.7 The probability sequence of the equivalent load

3.3 负载供电率概率性约束的确定性计算

为计算负载供电率满足概率，定义0-1变量[18]为

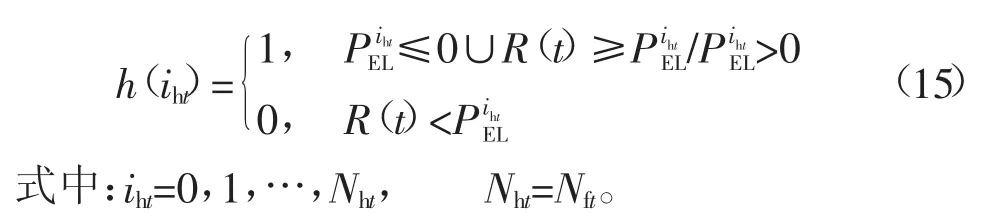
式（15）表明：在t时刻如果风光的共同出力满足负荷需求或者在风光的共同出力不满足负荷需求时储能剩余容量满足剩余的负荷，此时对应的h（iht）则取1，其他的情况取0，则此时的负载供电率概率则是对所有满足情况的序列概率的累积，t时段负载供电率约束满足的概率可确定性计算为

当χ＞α时表示满足负载供电率机会约束，其中α为满足负载供电率的置信水平。

3.4 能量过剩率概率约束的确定性计算

基于同样的理论计算能量过剩率满足概率，定义0-1变量为

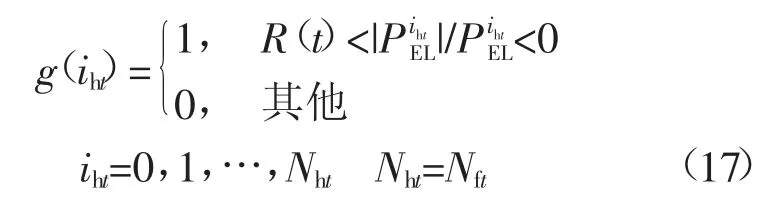
式（17）表明：在t时刻风光的共同出力满足负荷需求并且储能系统也不能完全消耗掉剩余的风光出力时，变量取1，否则取0。

则能量过剩率约束满足概率可确定性计算为

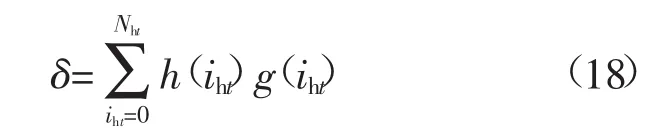
当δ＞β时表示满足能量过剩率机会约束，其中β为满足能量过剩率的置信水平。

3.5 优化算法流程

本文在计算确定性的约束概率时将概率序列与粒子群算法相结合，从而对微电网优化配置模型进行求解，算法流程图如图8所示。

图8 算法流程图Fig.8 Algorithm flow chart

4 算例分析

4.1 基础数据

如图9、10为某地区的典型月份的每小时天气数据，图11为每小时负荷功率数据，T=720 h。选择单台风力发电机容量为300 W，单个太阳能光伏电池模块容量为300 W，单个蓄电池单元额定容量为1.2 kW·h、额定功率为1.2 kW，它们的成本和相关费用数据见文献[19]，电池储能系统的初始剩余电SOC（0）=0.5，假设各个电源的使用年限均为15 a。

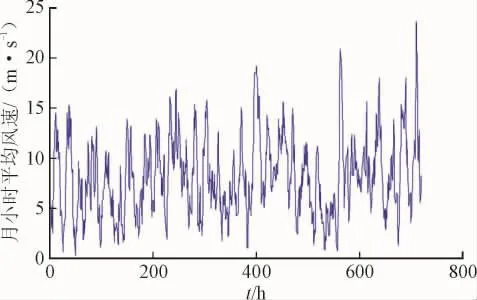
图9 典型月份的每小时风速Fig.9 Hourly wind speed in a typical month

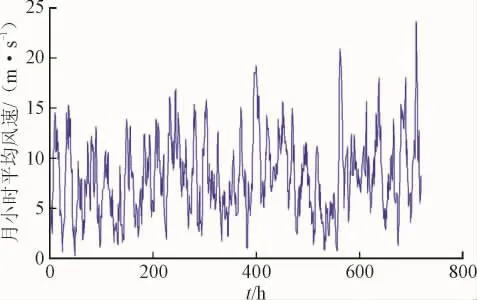
图10 典型月份的每小时光照强度Fig.10 Hourly light intensity in a typical month

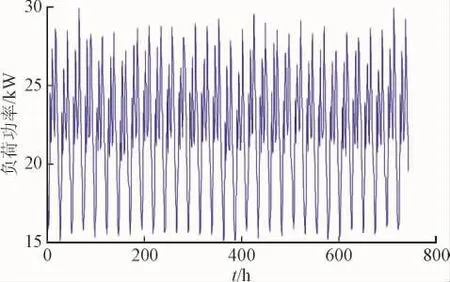
图11 典型月份的每小时负荷Fig.11 Hourly load ina typical month

4.2 不同负载供电率对优化配置结果的影响

设定能量过剩率β为100%，负载供电率α分别为100%、95%、90%时[20]，微网优化配置的结果如表1所示。

由表1的优化结果对比看出，不管负载供电率α的取值为何值时，能量过剩率δ都低于设定值β的100%，这表明风机出力、光伏电池出力和蓄电池之间在能量过剩率不到100%的情况下达到了一定的功率平衡。当风机出力和光伏电池出力过剩时可以给蓄电池充电，不足时蓄电池进行放电补偿，这样的优化配置结果降低了微网的经济投资成本。

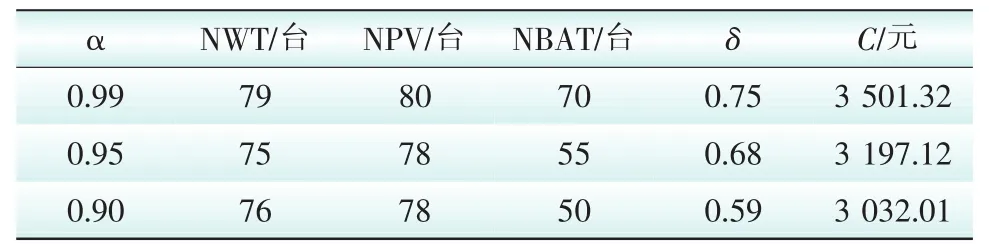
表1 微网优化配置结果Tab.1 Optimal allocation results of micro-grid

由表1可见，当负载供电率α由90%提高到95%时和α由95%提高到99%相比，前者综合成本增加的并不多，但是后者的综合成本相对大幅度增加，这是由于在负载供电率稍低时惩罚成本与电源与储能的购入成本相比比较低，可以由惩罚体系补偿可靠性的提高。但是随着可靠性的提高，在负荷较重时段需要更多的电源和储能才能满足需求，此时惩罚费用已经不能补偿负载供电率的提高，必须要增加微源和储能容量从而使得综合成本增加。合适的负载供电率水平对配置经济性有很大的影响。

4.3 负载供电率和能量过剩率的关系

1）在设定负载供电率α为99%的情况下，计算不同能量过剩率对负载供电率α的影响，结果如图12所示。

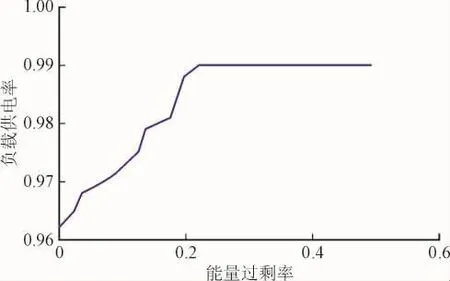
图12 能量过剩率和负载供电率的关系Fig.12 Relationship between excess energy and load power supply

由图12的关系曲线分析当能量过剩率置信水平β设置相对较高时，负载供电率α始终等于设定值0.99，表明微网系统不仅能达到可靠性指标，也能保证能量过剩率符合设定值要求。但是当能量过剩率β逐渐减小到0.2附近时，负载供电率则开始降低小于期望值，此时微网已经不能达到可靠性指标，需要通过降低可靠性水平来达到能量过剩率要求。当能量过剩率继续减小时，由图12可见系统负载供电率将迅速下降。

2）设定能量过剩率为100%，仿真计算负载供电率可靠性和能量过剩率。

由图13关系曲线分析能量过剩率随着负载供电率水平的降低而逐渐下降，这表明在负载供电率降低时微网在满足可靠性指标的同时会减少安装微电源数量来降低综合成本和能量的浪费惩罚。

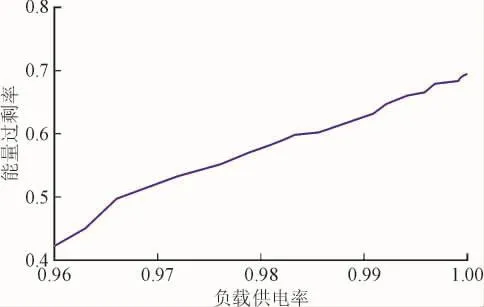
图13 能量过剩率和负载供电率的关系Fig.13 Relationship between excess energy and load power supply

这2种情况对比可看出负载供电率与能量过剩率是属于矛盾关系：可靠性指标是希望系统每时每刻都能满足负荷的需求，而能量过剩率是希望微源出力与储能系统每时每刻达到平衡没有剩余，本身两者在定义上就有一定的矛盾关系，而这样的理想情况一般无法达到。所以决策者可根据实际系统设计的要求选择合适的可靠性水平和能量过剩率水平。

4.4 离散化步长对负载供电率水平的影响

设定负载供电率α=95%，能量过剩率β=0.2时，不同的离散化步长对负载供电率的影响如图14所示。

图14 离散化步长对负载供电率水平的影响Fig.14 The influence of the discrete step size on the power supply rate

如图14取一天的24个小时数据分析，当负荷较小时，系统的微源出力与储能容量满足负荷需求，离散化步长对负载供电率的影响并不明显；当负荷较重时，离散化步长越精细，此时负载供电率越接近于置信水平。因此选择合理的公共步长也会对优化配置结果会有影响。

4.5 与传统模拟方法运行比较

大多数机会约束规划求解都是采用随机模拟的方法，本文将随机模拟和粒子群算法相结合，每次迭代对随机变量模拟N次，根据大数定律估计概率，满足规划约束的次数为N′，当N′/N＞α时机会约束满足。设定能量过剩率为β=0.2时分别采用随机模拟法和本文的算法求解配置结果如表2所示。

表2 随机模拟法和本文算法的配置结果Tab.2 The allocation results of the random simulation method and the algorithm of this paper

由表2可知，将负载供电率置信水平设定为99%时，随机模拟法和序列运算法的计算所用时间都大幅度增加，序列运算方法的主要耗时是粒子群算法每次迭代中新粒子的可靠性约束和能量过剩率约束的判断，这些约束都是定量性计算可得。而随机模拟法判断约束时耗时于机会约束大量模拟计算，需要大量的模拟计算才能保证结果的正确性，相比较序列运算方法节省了计算时间。

5 结语

本文将风机出力、光伏出力和负荷作为随机变量，采用机会约束规划方法建立微网优化配置模型。应用序列运算理论与粒子群算法相结合的方法将机会约束规划转化为定量性的概率计算，以概率形式准确表示微网运行约束。通过仿真分析可得出：微网的综合经济成本随着负载供电率的提高而增长，因此设定合理的可靠性置信水平可以降低多余投资；微网系统的负载供电率与能量过剩率之间属于矛盾关系，两者不可能同时都处于最佳水平，因此根据系统需求设定合适的负载供电率可靠性和能量过剩率水平对优化配置结果有改善效果；在采用序列运算理论与粒子群算法相结合的方法时需要选择合适的离散化步长提高优化配置约束的计算精确度。微网优化配置结果的影响因素太多，本文针对不确定性因素提出了新的处理方法寻优解得经济成本最优的微网电源装机数量的配置方案。

[1]刘舒，李正力，王翼，等.含分布式发电的微电网中储能装置容量优化配置[J].电力系统保护与控制，2016，44（3）：78-84.LIU Shu，LI Zhengli，WANG Yi，et al.Optimal capacity allocation of energy storage in micro-grid with distributed generation[J].Power System Protection and Control，2016，44（3）：78-84（in Chinese）.

[2]赵冬梅，尹颢涵，王建锋.间歇性能源出力特性综合分析体系及其应用[J].南方电网技术，2015，9（5）：7-14.ZHAO Dongmei，YIN Haohan，WANG Jianfeng.Comprehensive analysis system of intermittent energy output characteristics and its application[J].Southern Power System Technology，2015，9（5）：7-14（in Chinese）.

[3]丁明，王波，赵波，等.独立风光柴储微网系统容量优化配置[J].电网技术，2013，37（12）：575-581.DING Ming，WANG Bo，ZHAO Bo，et al.Configuration optimization of capacity of standalone PV-wind-dieselbattery hybrid microgrid[J].Power System Technology，2013，37（12）：575-581（in Chinese）.

[4]何俊，邓长虹，徐秋实，等.基于等可信容量的风光储电源优化配置方法[J].电网技术，2013，37（3）：3317-3324.HE Jun，DENG Changhong，XU Qiushi，et al.Optimal configuration of distributed generation system containing wind PV battery power sources based on equivalent credible capacity theory[J].Power System Technology，2013，37（3）：3317-3324（in Chinese）.

[5]程晓悦，卢锦玲.考虑不确定性的分布式电源多目标优化配置[J].电力科学与工程，2014，30（11）：16-21.CHENG Xiaoyue，LU Jinling.Multi-objective planning of distributed generations considering uncertainties[J].Electric Power Science and Engineering，2014，30（11）：16-21（in Chinese）.

[6]夏澍，顾劲岳，葛晓琳，等.风光联合优化配置的多目标机会约束规划方法[J].电力系统保护与控制，2016，44（6）：35-40.XIA Shu，GU Jinyue，GE Xiaolin，et al.Multi objective chance-constrained programming method for wind generations and photovoltaic allocating[J].Power System Protection and Control，2016，44（6）：35-40（in Chinese）.

[7]余金龙，赵文会，赵波，等.基于多状态建模的独立型微网优化配置[J].电力系统自动化，2015，39（6）：11-17.YU Jinlong，ZHAO Wenhui，ZHAO Bo，et al.Optimal configuration of standalone micro-grid based on miltistate modeling[J].Automation of Electric Power Systems，2015，39（6）：11-17（in Chinese）.

[8]鲜杏，范传光，文闪闪，等.考虑可再生能源随机性的孤岛微网容量优化配置方法[J].武汉大学学报（工学版），2016，49（1）：100-105.XIAN Xing，FAN Chuanguang，WEN Shanshan，et al.Optimal deployment for island micro-grid considering probabilistic factors of renewable energy generations[J].Engineering Journal of Wuhan University，2016，49（1）：100-105（in Chinese）.

[9]张建华，王昕伟，蒋程，等.基于蒙特卡罗方法的风电场有功出力的概率性评估[J].电力系统保护与控制，2013，42（3）：82-87.ZHANG Jianhua，WANG Xinwei，JIANG Cheng，et al.Probabilistic assessment of wind farm active power based on monte-carlo simulation[J].Power System Protection and Control，2013，42（3）：82-87（in Chinese）.

[10]赵文会，余金龙，李士动.基于SMCS-NSGAⅡ的独立型微网优化配置[J].电力系统保护与控制，2016，44（1）：97-105.ZHAO Wenhui，YU Jinlong，LI Shidong.Optimal configuration of standalone micro-grid based on SMCS-NSGAⅡalgorithm[J].Power System Protection and Control，2016，44（1）：97-105（in Chinese）.

[11]王敏.分布式电源的概率建模对电力系统的影响[D].合肥：合肥工业大学，2010.

[12]杨秀，陈洁，朱兰，等.基于经济调度的微网储能优化配置[J].电力系统保护与控制，2013，41（1）：53-59.YANG Xiu，CHEN Jie，ZHU Lan，et al.Optimization allocation of energy storage for micro-grid based on economic dispatch[J].Power System Protection and Control，2013，41（1）：53-59（in Chinese）.

[13]马艺玮.独立微电网分布电源优化配置与协调控制[D].广州：华南理工大学，2010.

[14]沈玉明.微电网电源容量优化配置与最优经济运行的模型和算法研究[D].重庆：重庆大学，2014.

[15]刘方，杨秀，时珊珊，等.不同时间尺度下基于混合储能调度的微网能量优化[J].电网技术，2014，38（11）：3079-3087.LIU Fang，YANG Xiu，SHI Shanshan，et al.Hybrid energy storage scheduling based micro-grid energy optimization under different time scales[J].Power System Technology，2014，38（11）：3079-3087（in Chinese）.

[16]朱兰，严正，杨秀，等.计及需求侧响应的微网综合资源规划方法[J].中国电机工程学报，2014，34（16）：2621-2628.ZHU Lan，YAN Zheng，YANG Xiu，et al.Integrated resources planning in micro-grid based on modeling demand response[J].Proceedings of the CSEE，2014，34（16）：2621-2628（in Chinese）.

[17]金鹏，艾欣，许佳佳.基于序列运算理论的孤立微电网经济运行模型[J].中国电机工程学报，2012，32（25）：52-60.JIN Peng，AI Xin，XU Jiajia.An economic operation model for isolated microgrid based on sequence operation theory[J].Proceedings of the CSEE，2012，32（25）：52-60（in Chinese）.

[18]刘方，杨秀，时珊珊，等.基于序列运算的微网经济优化调度[J].电工技术学报，2015，30（20）：227-237.LIU Fang，YANG Xiu，SHI Shanshan，et al.Economic operation of micro-grid based on sequence operation[J].Transactions of China Electrotechnical Society，2015，30（20）：227-237（in Chinese）.

[19]李成.微网系统中储能的优化配置与运行的研究[D].上海：上海电力学院，2013.

[20]王晶，陈江斌，束洪春.基于可靠性的微网容量最优配置[J].电力自动化设备，2014，34（4）：120-127.WANG Jing，CHEN Jiangbin，SHU Hongchun.Microgrid capacity configuration optimization based on reliability [J].Electric Power Automation Equipment，2014，34（4）：120-127（in Chinese）.

[21]武星，殷晓刚，宋昕，等.中国微电网技术研究及其应用现状[J].高压电器，2013，49（9）：142-149.WU Xing，YIN Xiaogang，SONG Xin，et al.Research on micro-grid and its application in china[J].High Voltage Apparatus，2013，49（9）：142-149（in Chinese）.

[22]胡林献，顾雅云，姚友素.并网型风光互补系统容量优化配置方法[J].电网与清洁能源，2016，32（3）：120-126.HU Linxian，GU Yayun，YAO Yousu.Optimal capacity configuration method for grid-connected wind-solar complementary power system[J].Power System and Clean Energy，2016，32（3）：120-126（in Chinese）.

Optimal Allocation of Micro-Grid Based on PSO and Sequence Operation Theory

XIA Hui1，YANG Xiu1，YANG Fan1，LIU Wenfei1，ZHANG Chunli2
（1.School of Electrical Engineering，Shanghai University of Electric Power，Shanghai 200082，China；2.Pudong Power Supply Company，State Grid Shanghai Electric Power Company，Shanghai 200120，China）

Considering the uncertainty of wind turbine output，photovoltaic output and load fluctuation in the optimal allocation of the independent micro-grid，a chance constrained programming model is built in this paper with the comprehensive economic cost as the optimal objective function and with power supply reliability and the energy surplus rate meeting the the restraint condition.Probability sequence is used to represent random variables based on the theory of sequence operation，the probability sequence and the particle in particle swarm optimization algorithm are combined to solve the probability sequence of the common output and the equivalent load in every moment，and then quantitatively calculate the probability of the constraint to solve the optimal number of micro source installation.This method helps to make the optimal allocation result more accurate and avoids the time consuming disadvantages of the traditional simulation method and overcomes the shortcoming that the result of each solution is different.

micro-grid；optimal allocation；chance constrained programming；sequence operation

2016-08-17。

夏 惠（1991—），女，硕士研究生，研究方向为含分布式电源的优化规划；

（编辑 冯露）

国家自然科学基金（51407114）。

Project Supported by the National Science Foundation of China（NSFC）（51407114）.

1674-3814（2017）04-0040-08

TM73

A

杨 秀（1972—），男，教授，硕士生导师，研究方向为分布式发电与微电网的运行与仿真。