一种新型交直流系统混合仿真方法
赵云灏,刘崇茹,李庚银,李越,罗钢
(1.新能源电力系统国家重点实验室(华北电力大学),北京 102206;2.广东电网有限责任公司电力调度控制中心,广东广州 510600)
一种新型交直流系统混合仿真方法
赵云灏1,刘崇茹1,李庚银1,李越1,罗钢2
(1.新能源电力系统国家重点实验室(华北电力大学),北京 102206;2.广东电网有限责任公司电力调度控制中心,广东广州 510600)
为发挥电磁暂态仿真方法和动态相量仿真方法的优势,提出了一种新型交直流系统混合仿真方法——交流系统使用电磁暂态模型、直流系统使用动态相量模型的电磁-动态相量混合仿真方法来分析交直流系统扰动情况下系统的动态过程,根据交直流系统位置和相互作用关系,分析了混合仿真中交直流系统模型的接口位置、等效方法以及混合仿真方法。将所提出的混合仿真的仿真结果和PSCAD/EMTDC中的电磁暂态模型仿真结果进行了比较,验证了所提交直流系统电磁-动态相量混合仿真方法的正确性和有效性。
交直流系统;动态相量;电磁暂态
随着电力电子器件制造技术的提高以及远距离大容量输电的需求,高压直流输电技术在国内外得到广泛应用。尤其在中国,为解决能源中心和负荷中心距离较远的现状,高压直流系统在能源中心向负荷中心送电、跨区互联中发挥了重要作用,形成了跨区互联、交直流并列运行的世界上最复杂的交直流混合系统[1]。为研究交直流系统的动态过程,开展关于不同详细程度、适合不同研究用途的交直流系统仿真模型以及仿真方法的研究,已成为研究人员多年来的研究重点。
目前电力系统时域仿真中广泛使用的仿真模型可分为两类:电磁暂态模型[2-3]和机电暂态模型(或称为准稳态模型)[4]。其中,电磁暂态模型使用差分计算模型,能准确反映交直流系统各频次的动态特性,但是计算求解规模大,尤其在模拟换流器等电力电子器件时更为明显;机电暂态模型使用基波相量模型,计算求解规模小,但该模型对交流系统及直流系统换流器均采用准稳态模型,不够精确。为了综合解决仿真精度和计算规模的问题,动态相量建模理论[5]因其在换流器等电力电子器件建模中的优势被引入到电力系统建模仿真中。其原理是通过对时变信号进行傅里叶变换,导出其主导分量对应的时变傅里叶系数,以建立能反映元件动态特性的动态相量模型。该方法已在HVDC换流器及HVDC系统[6-7]、FACTS元件[8]以及 dc-dc变换器[9]等电力电子器件建模中得到成功应用。为充分发挥3种模型在交直流系统建模仿真中的优势,文献[10-12]分别对交直流系统动态相量仿真以及交直流系统机电-动态相量、机电-电磁混合仿真进行了相关研究。
为结合电磁暂态仿真和动态相量建模方法的优势,充分发挥电磁暂态仿真方法的优势,需建立一套交流系统模型,既可反映交流系统基波及各次谐波全部动态特性的优势,同时又能有效利用直流系统动态相量模型;既可根据仿真精度的需要,建立换流器主要特征谐波的数学模型的特点,又能将换流器模型处理成代数模型,以减少建模和仿真计算的复杂度。本文使用文献[7]提出的直流系统动态相量模型,提出了交流系统使用电磁暂态模型,直流系统使用动态相量模型的交直流系统电磁-动态相量混合仿真方法。
本文根据电磁暂态仿真和动态相量建模仿真方法的优点与原理,以及交直流系统相互关系,分析了交直流系统电磁-动态相量混合仿真中交直流系统的分区、相互等效方法以及混合仿真算法。在MATLAB中编程实现了提出的交直流系统电磁-动态相量混合仿真。将混合仿真结果与PSCAD/EMTDC中的交直流系统电磁暂态模型仿真结果进行了对比,验证了所提出的交直流系统电磁-动态相量混合仿真的可行性和准确性。
1 电磁暂态模型和动态向量模型的基本原理
1.1 电磁暂态模型基本原理
电磁暂态数值计算方法以微分方程的隐式梯形积分法为基础。因为隐式梯形积分法在求解微分方程中具有极高的求解精度及计算稳定性,因此电磁暂态仿真能准确反应电感、电容等基本电器元件以及电力滤波器和传输线等交流系统元件的动态特性。
以电感元件为例对电磁暂态模型数值计算方法进行说明,电感元件的时域微分方程为

式中:uL为电感两端的电压;iL为流过电感的电流。应用隐式梯形积分法,可将式(1)转化为差分方程(2)求解

式中:Δt为积分求解步长。
交流系统电磁暂态过程的计算方法和流程参见文献[13]。
1.2 动态相量模型基本原理
动态相量模型的数学基础是傅里叶变换。对于时域中周期为T的函数x(τ),在任一时间长度为(t-T,t]的区间上可以用傅里叶级数表示为[5]

式中:ω=2π/T;Xk(t)为k次时变的傅里叶系数,称为k阶动态相量,记为〈x〉k。
根据动态相量的基本理论可知,时域值到动态相量值的转换可通过下列数值积分完成:

式中:N=T/Δt;Δt为积分求解步长。
根据k阶动态相量的定义可知,动态相量具有:
1)共轭特性

上标“*”表示共轭复数。
2)微分特性

3)卷积特性

利用动态相量理论以及直流系统换流器的调制理论,可方便地建立能反映换流器谐波动态特性的换流器动态相量模型以及直流线路的动态相量微分模型和直流系统控制器动态相量模型。
2 交直流系统电磁动态相量混合仿方法
混合仿真中交流系统使用电磁暂态模型;直流系统使用文献[7]提出的直流系统动态相量模型,该模型包含完整的换流器动态相量模型、直流系统动态相量模型以及定电流控制器、定电压控制器以及低压限流环节等控制系统模型。另外文献[7]提出的直流系统动态相量模型未建立锁相环(PLL)模型,为实现混合仿真,完善直流系统控制系统模型,本文根据文献[14]建立了PLL模型。
2.1 交直流系统分区及等效
混合仿真中,为方便交直流系统分区,发挥直流系统动态相量模型的优势,选取整流侧以及逆变侧换流母线作为电磁-动态相量混合仿真模型的接口。
根据交直流系统仿真过程中的相互关系以及交直流系统混合仿真的分区及接口位置的选取,交流系统在换流母线处对直流系统等效为电压源,直流系统在换流母线处对交流系统等效为电流源。此外,因直流系统直流侧滤波电感的作用,直流系统换流器的直流侧考虑直流量;交流侧电流根据换流器的组成形式,考虑基波以及主要特征谐波电流,如12脉动换流器,交流侧考虑基波以及11次和13次谐波电流。
2.2 混合仿真算法
混合仿真方法为:首先根据交直流系统位置建立交流系统电磁暂态计算网络,并将直流线路的动态相量模型、控制器模型以及PLL模型差分化;其次将交流系统电磁暂态模型、换流器动态向量模型以及差分后的直流线路动态相量模型和控制器模型、PLL模型配合,进行仿真,仿真流程图如图1所示。

图1 交直流系统电磁-动态相量混合仿真流程图Fig.1 The flowchart of EMT-DP hybrid simulation of AC-DC system
混合仿真流程如下:
步骤1 以整流侧和逆变侧的换流母线为边界,根据交流系统的滤波器等各元件连接方式及直流系统位置形成式(8)所示的交流系统电磁暂态计算网络的节点方程,并根据潮流计算结果设定仿真初值。

式中:G为根据交流系统元件形成的电磁暂态计算节点导纳矩阵;uac(t+Δt)为t+Δt时刻交流系统各节点瞬时电压组成的列向量;ihistory(t)为根据t时刻交流系统各节点电压值uac(t),各支路电流值iac(t)。两侧换流母线注入直流系统的电流的时域值ir(t)、ii(t)组成的历史电流列向量。
步骤2 根据式(8)计算得到t+Δt时刻各节点的瞬时电压值uac(t+Δt)。
步骤3 根据交流系统元件差分模型计算得到t+Δt时刻交流系统各支路的电流值iac(t+Δt)。
步骤4 根据t时刻和t+Δt时刻两侧换流母线的交流电压值,t时刻换流母线a相电压相角θrva(t)、θiva(t),由PLL差分模型计算t+Δt时刻两侧换流母线电压的相角θra(t+Δt)、θia(t+Δt)。
步骤5 通过时域值向动态相量值转换的公式式(5),计算得到t+Δt时刻的两侧换流母线a相电压的动态相量值〈vra〉1(t+Δt)、〈via〉1(t+Δt)。
步骤6 根据t+Δt时刻两侧换流母线a相电压的动态相量值αr(t)、αi(t)控制器输出的,以及文献[7]中直流系统动态相量模型计算得到的两侧换流器的换相角μr(t)、μi(t),通过文献[7]中整流器和逆变器动态相量模型的直流电压部分,计算得到t+Δt时刻直流系统整流侧和逆变侧的直流电压动态相量值〈vdr〉0(t+Δt)、〈vdi〉0(t+Δt)。
步骤7 根据t+Δt时刻直流侧直流电压动态相量值〈vdr〉0(t+Δt)、〈vdi〉0(t+Δt),t时刻直流侧直流电压〈vdr〉0(t)、〈vdi〉0(t)、〈vdc〉0(t)以及t时刻直流系统整流侧、逆变侧和直流线路对地电容的电流动态相量值〈idr〉0(t)、〈idi〉0(t)、〈idc〉0(t),通过差分后的直流线路动态相量模型计算得到t+Δt时刻直流侧直流电流动态相量值〈idr〉0(t+Δt)、〈idi〉0(t+Δt)、〈idc〉0(t+Δt)以及直流线路对地电容的电压动态相量〈vdc〉0(t+Δt)。
步骤8 根据t+Δt时刻直流侧直流电压、电流动态相量〈vdr〉0(t+Δt)、〈vdc〉0(t+Δt)、〈vdi〉0(t+Δt)和〈idr〉0(t+Δt)、〈idi〉0(t+Δt)、〈idc〉0(t+Δt)以及动态相量与时域值转换公式计算得到t+Δt时刻直流侧直流电压、电流的时域值vdr(t+Δt)、vdc(t+Δt)、vdi(t+Δt)和idr(t+ Δt)、idc(t+Δt)、idi(t+Δt)。
步骤9 根据t+Δt时刻直流侧直流电流动态相量值〈idr〉0(t+Δt)和〈idi〉0(t+Δt),t时刻整流侧和逆变侧触发角αr(t)、αi(t),文献[7]中模型计算得到的两侧换流器的换相角μr(t)、μi(t)以及PLL计算得到的t+Δt时刻的整流侧、逆变侧的a相电压相角θra(t+Δt)、θia(t+ Δt)和整流侧、逆变侧换流母线a相电压的初相位,利用文献[7]中整流器和逆变器动态相量模型交流电流部分以及动态相量到时域值的定义,计算得到t+ Δt时刻两侧换流母线注入直流系统的电流值ira(t+ Δt)、irb(t+Δt)、irc(t+Δt)和iia(t+Δt)、iib(t+Δt)、iic(t+Δt)。
步骤10 根据t+Δt时刻直流侧直流电压、电流动态相量值〈vdi〉0(t+Δt)、〈idr〉0(t+Δt)、〈idi〉0(t+Δt)以及t时刻直流侧直流电压、电流动态相量〈vdi〉0(t)、〈idr〉0(t)、〈idi〉0(t),由控制器差分模型计算得到t+Δt时刻整流侧和逆变侧的触发角αr(t+Δt)、αi(t+Δt)。
步骤11 令t=t+Δt,检测是否t=tt_end;如果是,则仿真结束;如果不是,返回步骤1循环。

图2 单极12脉动HVDC系统Fig.2 A monopolar 12-pules HVDC transmission system
3 仿真结果
本文仿真测试系统为图2所示的单极12脉动高压直流系统。系统参数为:交流系统频率50 Hz,整流侧交流系统电源线电压有效值为382.867 2 kV,整流侧换流变压器变比为1/Kr=345/213.455 7,逆变侧交流系统电源线电压有效值为215.05 kV,逆变侧换流变压器变比为1/Ki=230/209.228 8,整流侧和逆变侧的换流变压器漏抗标幺值均为0.18 pu,整流侧及逆变侧换流母线处均装有11次及13次滤波器和无功补偿装置。直流系统额定电压500 kV,额定电流2 kA,直流线路电阻5 Ω,直流线路整流侧和逆变侧的平波电感均为0.596 8 H,直流线路对地电容50 μF。控制系统整流侧采用定电流控制,逆变侧采用定电压控制,同时整流侧和逆变侧均配有低压限流环节。
在电磁暂态仿真程序PSCAD/EMTDC中,建立了图2所示的交直流系统电磁暂态模型。应用所提出的交直流系统电磁-动态相量混合仿真方法,使用Matlab编程实现了图2所示的交直流系统电磁-动态相量混合仿真。使用所建混合仿真模型与PSCAD/EMTDC中的电磁暂态模型在下列2种扰动情况进行了对比。
Case 1,HVDC系统直流电流参考值Idref在t=2 s时从1 pu变化到0.6 pu。
Case 2,整流侧交流电源电压在t=2 s时跌落5%,这类故障一般是由远方系统发生故障引起的[16]。
2种扰动下混合仿真和电磁暂态仿真所得的直流系统整流侧直流电流以及整流侧换流母线a相交流电压、整流侧换流母线流向直流系统的a相交流电流分别如图3—图5所示,其中idrHybrid、vraHybrid、iraHybrid是所提交混合仿真得到的直流电流以及交流电压、电流;idrEMT、vraEMT、iraEMT是电磁暂态仿真得到的直流电流以及交流电压、电流。
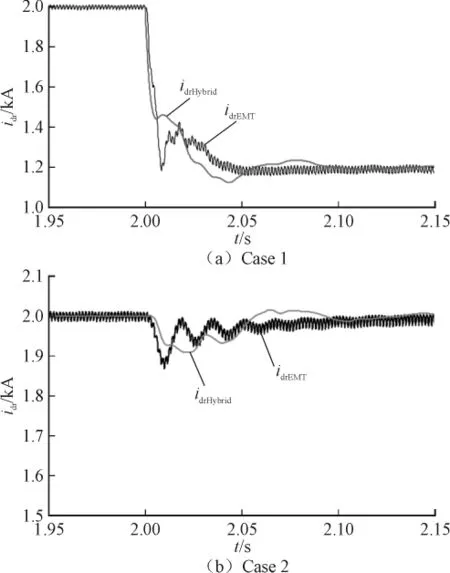
图3 直流电流仿真结果对比Fig.3 Simulation results of the direct current
图3—图5的仿真结果可以看出,交直流系统混合仿真在直流系统和交流系统扰动下能很好地反映交直流系统的动态特性,并能很好地反映直流系统换流器的谐波特性。
对比的仿真结果中,电磁暂态模型仿真步长为50 μs,混合仿真仿真步长为100 μs。因为在不同平台建立了电磁暂态模型和混合仿真模型,不能直接对比仿真速度,但混合仿真的仿真步长比电磁暂态仿真的仿真步长大,而且动态相量建模方法通过代数方程,既可建立能准确反映换流器频率特性的换流器模型,又能有效降低计算求解规模(与电磁暂态计算方法相比)。文献[6]对动态相量仿真方法能有效减少仿真时间进行了详细分析。因此可知混合仿真能有效反映交直流系统动态特性,并能有效提高仿真速度。
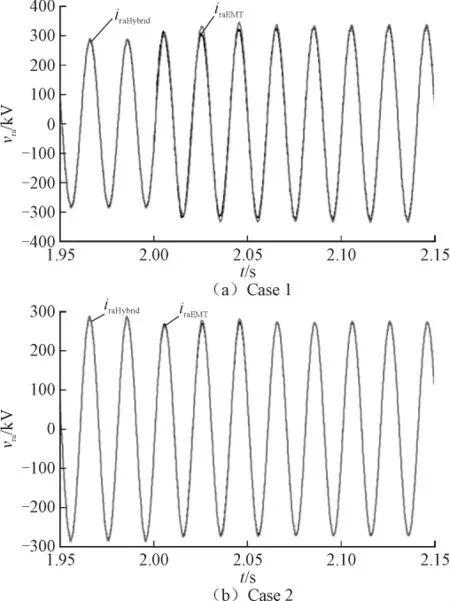
图4 整流侧换流母线电压仿真结果对比Fig.4 Simulation results of the commutation bus voltage in the rectifier side

图5 整流侧换流母线流向直流系统电流仿真结果对比Fig.5 Simulation results of the AC current in the rectifier side
4 结论
为发挥电磁暂态建模仿真方法以及动态相量建模仿真方法各自的优势,本文提出了一种新型交直流系统混合仿真方法-交流系统使用电磁暂态模型,直流系统使用动态相量模型的交直流系统电磁-动态相量混合仿真方法,详细分析了混合仿真的实现流程。
MATLAB中混合仿真结果和PSCAD/EMTDC中电磁暂态模型仿真结果的对比分析表明,所提出的混合仿真能在使用比直流系统电磁暂态模型简单易求解的直流系统动态相量模型以及较大仿真步长时,在不同的交直流系统扰动下,准确反映交直流系统的动态过程,具有良好的仿真精度,验证了混合仿真的正确性和有效性。该混合仿真方法为交直流系统仿真提供了新思路。
[1]HUANG Daochun,SHU Yinbiao,PUAN Jiangjun,et al.Ultra high voltage transmission in China:developments,current status and future prospects[J].Proceedings of the IEEE,2009,97(3):555-583.
[2]ZHU Haojun,CAI Zexiang,GOLE A M,et al.Improved coherency-based wide-band equivalents for real-time digital simulators[J].IEEE Transaction on Power System,2011,26(3):1410-1417.
[3]KUNDER PRABHA.Power system stability and control [M].New York:McGraw-Hill,1994:545-557.
[4]BAHRMAN M P,JOHNSON B K.The ABCs ofHVDC transmission technologies[J].IEEE Power and Energy Magazine,2007,5(2):32-44.
[5]SANDERS S R,NOWOROLSHI J M,LIU X Z,et al.Generalized averaging method for power conversion circuits[J].IEEE Transactions on Power Electronics,1991,6(2):251-259.
[6]LIU Chongru,BOSE Anjan,TIAN Pengfei.Modeling and analysis of HVDC converter three-phase dynamic phasor [J].IEEE Transactions on Power Delivery,2014,29(1):3-12.
[7]戚庆茹,焦连伟,陈寿孙,等.高压直流输电动态相量建模与仿真[J].中国电机工程学报,2003,23(12):28-32.QI Qingru,JIAO Lianwei,CHENG Shousun,et al.Modeling and simulation of HVDC with synamic phasors [J].Proceedings of the CSEE,2003,23(12):28-32(in Chinese).
[8]FERMANDO C J,SERGIO G J R,GLAUCO N T.SSR results obtained with a dynamic phasor model of SVC using model analysis[J].Electrical Power and Energy System,2010,26(3):1744-1754.
[9]CALISKAN V A,VERGHESE O C,STANKOVIC A M.Multifrequency averaging of dc-dc converters IEEE Trans on Power Electronics,1999,14(1):124-133.
[10]DARYABAK M,FILIZADEH S,JATSKVICH J,et al.Modeling of LCC-HVDC systems using dynamic phasors [J].IEEE Transactions on Power Delivery,2014,29(4):1989-1998.
[11]朱浩骏,蔡泽祥,刘皓明,等.基于动态相量模型的交直流系统混合仿真[J].华南理工大学学报(自然科学版),2006,34(10):83-18.ZHU Haojun,CAI Zexing,LIU Haoming,et al.Hybrid simulation of AC/DC power system based on dynamic phasor model[J].Journal of South China University of Technology(Natural Science Edition),2006,34(10):83-18(in Chinese).
[12]陈磊,张侃君,夏勇军,等.基于ADPSS的高压直流输电系统机电暂态-电磁暂态混合仿真研究[J].电力系统保护与控制,2013,41(12):137-142.CHEN Lei,ZHANG Kanjun,XIA Yongjun,et al.Electromechanical-electromagnetic transient hybrid simulation on HVDC power transmission system based on ADPSS[J].Power System Protection and Control,2013,41(12):137-142(in Chinese).
[13]夏道止.电力系统分析(下册)[M].北京:水利电力出版社,1995:56-59.
[14]ÖGREN J.PLL design for inverter grid connection:simulations for ideal and non-ideal grid conditions[D/OL].[2017-01-01].Uppsala University,Available:http://www.divaportal.org/smash/record.jsf pid=diva2:430787.
(编辑 冯露)
A New Kind of Hybrid Simulation Method of AC-DC Power System
ZHAO Yunhao1,LIU Chongru1,LI Gengyin1,LI Yue1,LUO Gang2
(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources(North China Electric Power University),Beijing 102206,China;2.Power Dispatch Control Centre of Guangdong Power Grid Corp.Ltd.,Guangzhou 510660,Guangdong,China)
In order to take the advantage of electromagnetic transient(EMT)simulation method and dynamic phasors simulation method,this paper proposes a new hybrid simulation of AC-DC system-electromagnetic transient-dynamic phasors hybrid simulation of AC-DC System where dynamic phasors model and traditional EMT models are respectively applied to build the model of HVDC system and AC system.The location of the interface,equivalent method of AC-DC system and EMT-DP hybrid simulation method are investigated.Simulation results show that the proposed EMT-DP hybrid simulation of AC-DC system are both effective and acceptable.
AC-DC system;dynamic phasors;electromagnetic transient
2017-01-26。
赵云灏(1988—),男,博士研究生,主要研究方向为交直流混合系统分析与仿真、运行与控制;
刘崇茹(1977—),女,博士,教授,博士生导师,主要从事交直流混合系统分析与仿真、运行与控制的科研和教学工作;
李庚银(1964—),男,博士,教授,博士生导师,主要从事新能源电力系统、电能质量、新型输配电技术等方面的研究
高等学校学科创新引智计划(“111”计划)(B08013);广东电网有限责任公司科技项目(K-GD2014-198)。
Project Supported by the“111”Project(B08013)of China;Science and Technology Program of Guangdong Power Grid Company Limited(K-GD2014-198).
1674-3814(2017)04-0001-06
TM743
A

