两个正数的各种均值

徐望斌，陈敬华

(湖北师范大学数学与统计学院，湖北 黄石 435002)

两个正数的各种均值

徐望斌，陈敬华

(湖北师范大学数学与统计学院，湖北 黄石 435002)

给出了两个正数的各种均值的一种新的几何模型，并由此构造了两个正数的各种均值不等关系的一种证明．再对均值不等式进行了拓展，说明其应用。

两个正数；均值；几何模型

0 引言

两个正数的各种均值的不等性在数学中占有重要的地位，不等式的证明中经常用到两个正数的算术平均数、几何平均数、调和平均数和平方平均数之间的关系，也就是均值不等式[1]。本文通过对梯形中位线的性质联想，给出了这四种均值之间的不等关系的一种几何模型，再依照几何模型的性质给出了均值不等式的一种证明．再对均值不等式进行了拓展，说明其应用。

目前，关于两个正数a，b的各种均值主要有：

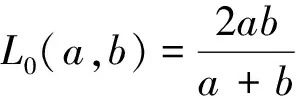
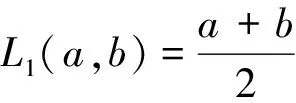
Lehmer 平均定义不了平方平均．

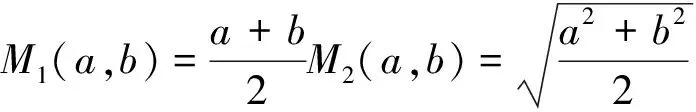
Mp(a,b)与Lp(a,b)都是p的严格单调增函数，从而得到均值不等式

1 均值不等式的几何模型

如图1：设梯形ABCD的上底AB的长为a，下底CD的长为b，不妨设0

f(θ)=a+θ(b-a),(0≤θ≤1)

易得函数的性质：

1)f(θ)=a+θ(b-a),(0≤θ≤1)是θ的增函数；

2) 当θ1+θ2=1(0≤θ1，θ2≤1)时，f(θ1)+f(θ2)=a+b；

3) 当θ1+θ2>1(0≤θ1，θ2≤1)时，f(θ1)+f(θ2)>a+b．

其次，θ的值以及对应f(θ)值如表1：

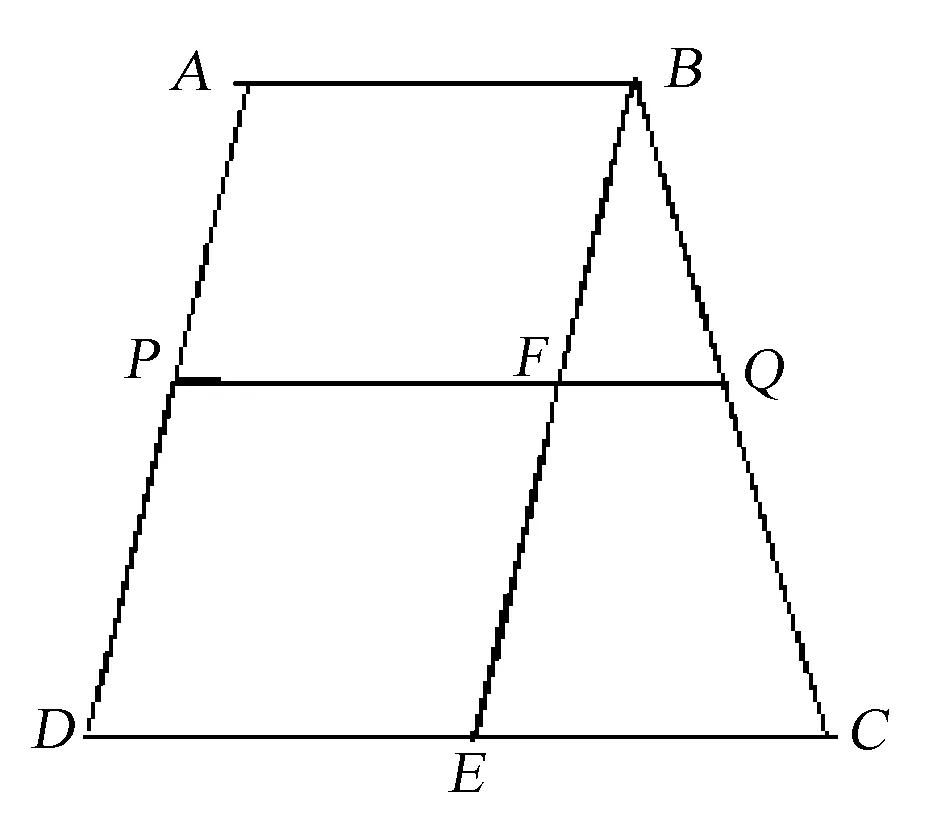
图1 几何模型

表1 θ与f(θ)的值

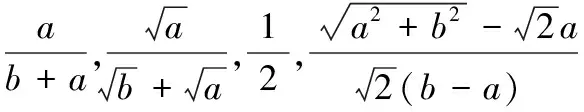
这样就从图形上直接得到了均值不等式，清楚明了．上式在a=b时，所有不等号变成等号．

从上面的推导也容易想到：均值不等式实际上是在两个数a,b(0

由f(θ)=a+θ(b-a),(0≤θ≤1)是θ的增函数，这样就从代数方面得到了均值不等式．

2 均值不等式的拓展及其应用

从上面的分析，易得均值不等式的拓展式：对正数a与b，有

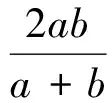
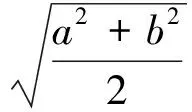
(1)

证明 当a=b时上式显然成立．

不妨设b>a，由f(θ)=a+θ(b-a),θ∈[0,1]的性质3)来证明．

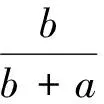
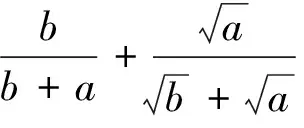
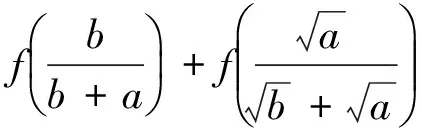
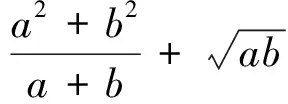
例2 设0≤θ≤1．对于已知正数a,b，证明：a+θ(b-a)≥a1-θbθ．

证明 令h(a)=a+θ(b-a)-a1-θbθ，则

h＇(a)=1-θ-(1-θ)a-θbθ

由h＇(a)=1-θ-(1-θ)a-θbθ=0

得a=b，又

h＂(a)=θ(1-θ)a-1-θbθ

显然，h＂(a)=θ(1-θ)a-1-θbθ>0，故当a=b时h(a)取得最小值h(b)=0 ．

∴h(a)≥h(b)=0

即a+θ(b-a)≥a1-θbθ

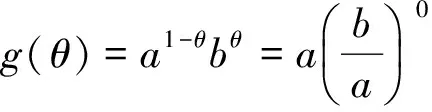
例3 设正数m,k满足m≥2k．对于已知正数a,b，证明：

是k的增函数，且

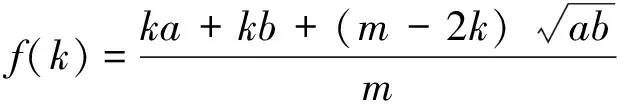
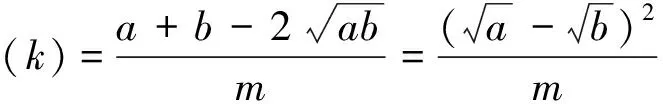
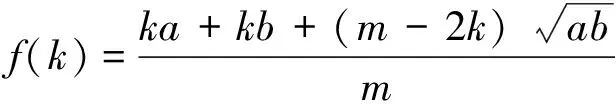
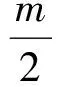
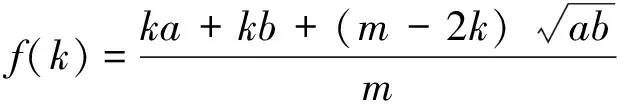
实际上，任选表格中的几个均值，把它们相加后除以均值的个数，其商也是分布在两正数a,b之间的正数，即对于不全为零的自然数ni,i=1,2,…,6 ．形如

是两正数a,b的均值．

3 结语

两个正数均值的几何模型把常见的几个均值进行了简洁直观的排序，便于记忆和理解，而且可以得到a和b之间的新均值．由此产生的函数式

f(θ)=a+θ(b-a)(b≥a,θ∈[0,1])

表示了两个正数的均值与这两个正数a和b之间的本质联系．另外，我们也发现

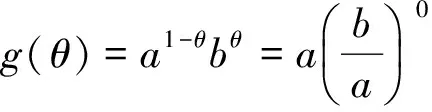
也同样表示了两个正数的均值与这两个正数a和b之间的本质联系．

[1]余元希,田万海等.初等代数研究(下册)[M].北京:高等教育出版社，1988.

[2]匡继昌.常用不等式[M].济南：山东科学技术出版社，2004.

[3]黄华平，胡松林.一个常见不等式的推广及其应用[J].湖北师范学院学报(自然科学版)，2012,32(3):96～100.

All kinds of mean values on two positive numbers

XU Wang-bin,CHEN Jing-hua

(School of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)

In this paper, a new geometric model on several average values for two positive numbers is obtained. A proof on mean value inequalities between two positive numbers is also given. Besides this, an expansion on them is still exhibited to illustrate the superioty of applications.

positive number;mean value;geometric model

2016—06—14

徐望斌(1965— )，男，湖北天门人，副教授，主要从事中学数学的教学研究.

O174

A

2096-3149(2017)01- 0093-04

10.3969/j.issn.2096-3149.2017.01.019