Several congruences involving harmonic numbers

YANG Jizhen， WANG Yunpeng

(1.Department of Mathematics, Luoyang Normal College, Luoyang, Henan 471934;2.Department of Mathematics and Physical, Luoyang Institute of Science and Technology, Luoyang, Henan 471022)

Several congruences involving harmonic numbers

YANG Jizhen1， WANG Yunpeng2*

(1.Department of Mathematics, Luoyang Normal College, Luoyang, Henan 471934;2.Department of Mathematics and Physical, Luoyang Institute of Science and Technology, Luoyang, Henan 471022)

The purpose of this paper is to establish several congruences involving harmonic numbers. Letp>3 be a prime. With the help of some combinatorial identities and congruences, the following congruences is generated:

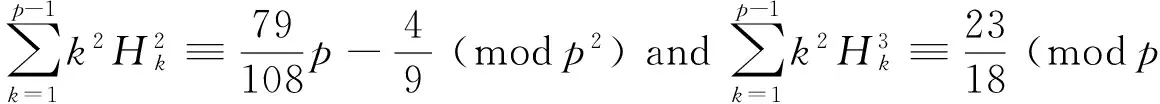
The congruences are also established as

and

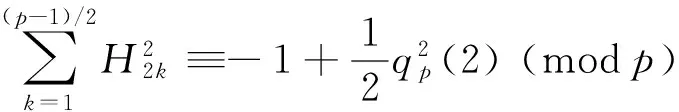
whereBn(n∈) are Bernoulli numbers andqp(a)=(ap-1-1)/pis usually called a Fermat quotient providedpa．

congruences; harmonic numbers; combinatorial identities

1Introduction

Harmonic numbers play important roles in number theory， analysis algorithms and special function. Forα∈， the generalized harmonic numbers are defined by

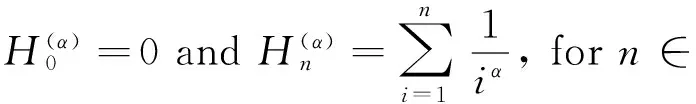
whenα=1， they reduce to the well-known harmonic numbers

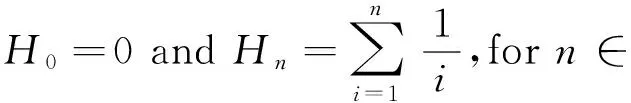
In 1862， Wolstenholme[1]proved that if p > 3 is a prime， then

(1)

which imply that

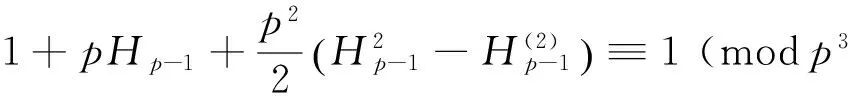
In 1938， LEHMER[2]showed

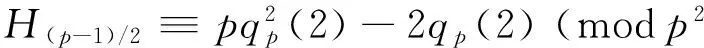
(2)

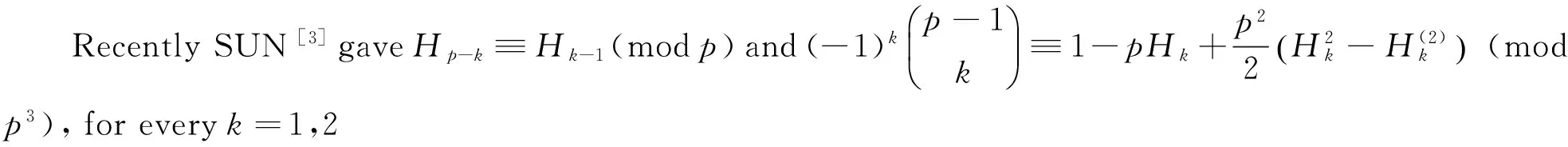
(3)

Using these congruences， SUN[3]obtained a series of congruences involving harmonic numbers. For example，

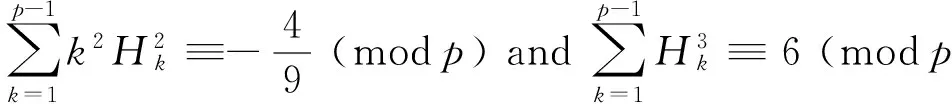
(4)

In this paper， we establish several congruences for sums involving harmonic numbers. Our main result is as follows．

2Main result

Theorem 1Letp> 3 be a prime. Then

(5)

and

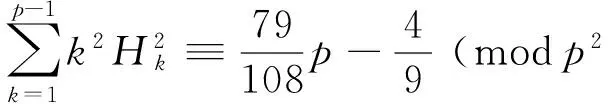
(6)

Theorem 2Letp> 3 be a prime. Then

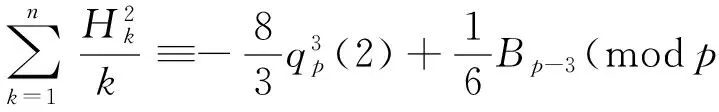
(7)

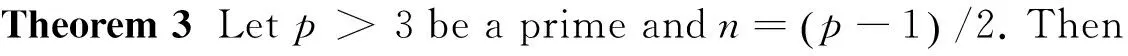
(8)

and

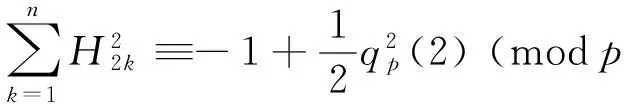
(9)

3Some lemmas

We first state some basic facts which will be used very often. For any prime p， it is well-known that

wherenis a integer. We also have

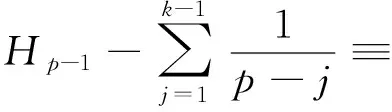
Thus

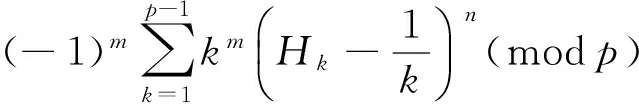
wheremis a integer and n is a positive integer. Whenp>3，

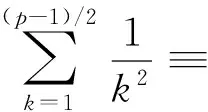
Lemma 1Letnbe a positive integer. Then

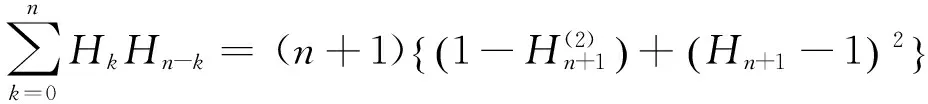
(10)

Whenn≥3， we have

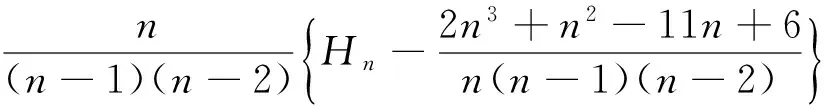
(11)

ProofBoth of the above identities are due to Wei (cf. [4， Theorem 1 and Theorem 6])．

Lemma 2 Letnbe a positive integer. Then

(12)

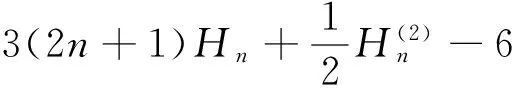
(13)

ProofThese two identities were deduced by Chen( cf. [5， (2.8)， (2.9)])．

).

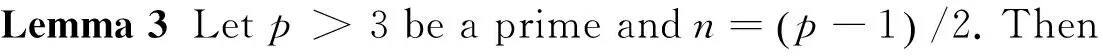
(14)

ProofWe have

Note that (cf. [6， Corollary5.2(b)])

(15)

and (cf. [7， (5.4)])

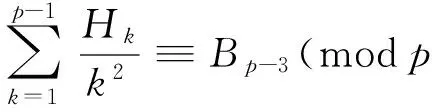
(16)

Therefore

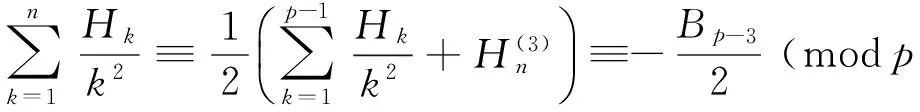
4The proofs of (5)-(9)

Proof of (5) Observe that

(modp).

In view of (3) and (4)， we have

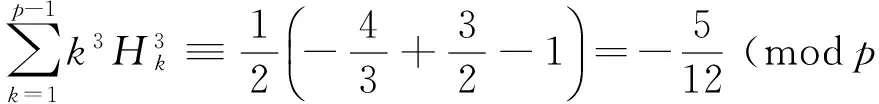
(17)

Since

(modp)，

we have

(modp).

Note that (cf. [3， Corollary1.1])

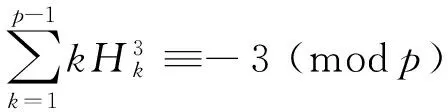
(18)

therefore

with the help of (4)， (17) and (18). This proves (5)．

Using the same method， we can deduce the following congruences:

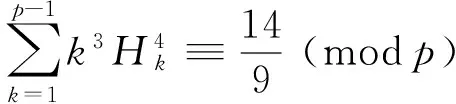
(19)

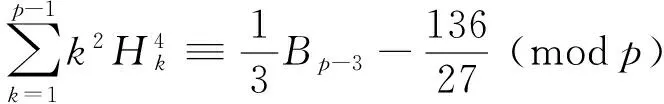
(20)

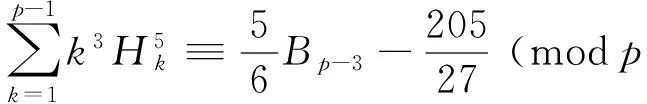
(21)

Whenp> 5 ， we have

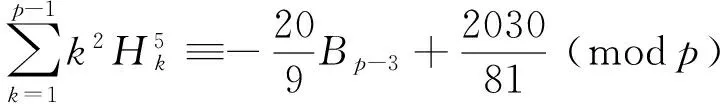
(22)

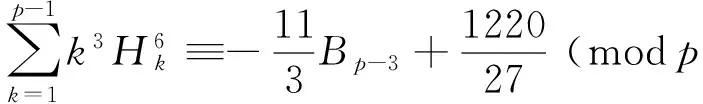
(23)

Proof of (6) Observe that

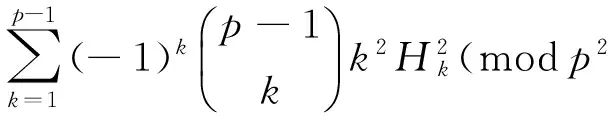
Takingn=p-1 in (11)， we have

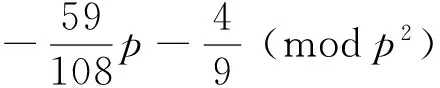
sinceHp-1≡0 (modp2). Hence

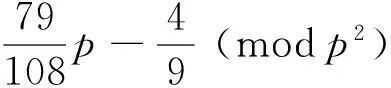
with the help of (5). This concludes the proof of (6)．

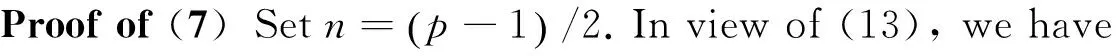
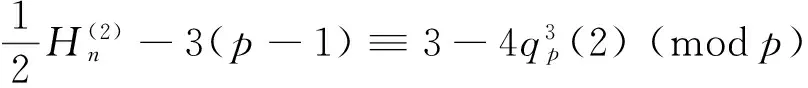
(24)

sinceH(p-1)/2≡-2qp(2) (modp). Observe that

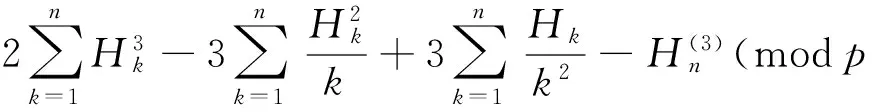
Thus

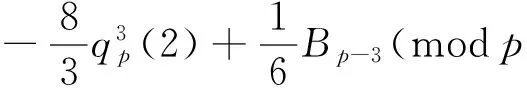
with the help of (4)， (14)， (15)， (24). This proves (7)．

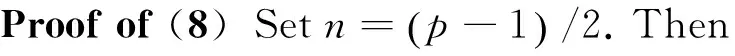
-2qp(2)+2H2k-Hk(modp)，

which implies that

Therefore

(modp).

In view of (10)， we have

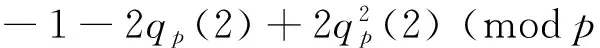
In light of (12)， we obtain

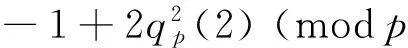
Also

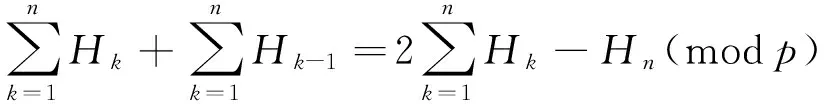
and hence

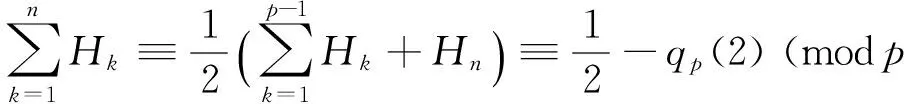
(25)

Combining the above， we obtain

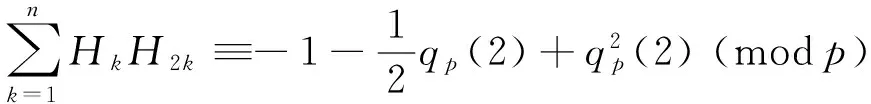
as desired．

Furthermore， we can deduce the following congruences:

(26)

and

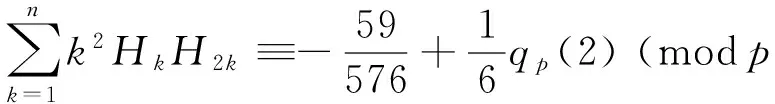
(27)

).

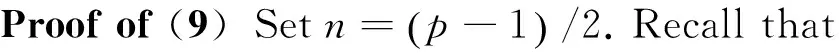
Thus

4HkH2k-8qp(2)H2k+4qp(2)Hk)≡

4HkH2k-4qp(2)Hn-k) (modp)，

which implies that

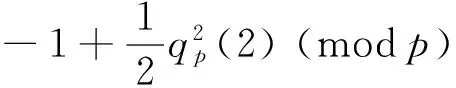
with the help of (8) and (25). The proof of (9) is now completed．

[1] WOLSTENHOLME J. On certain properties of prime numbers [J]. Quart J Math， 1862， 5: 35-39．

[2] LEHMER E. On congruences involving Bernoulli numbers and the quotients of Fermat and Wilson [J]. Ann of Math， 1938， 39: 350-360．

[3] SUN Z W. Arithmetic theory of harmonic numbers [J].Proc Amer Math Soc， 2012， 140: 415-428．

[4] WEI C A. Chu-Vandermonde convolution and harmonic number identities [J]. Integr Transf Spec F， 2014， 24: 324-330．

[5] CHEN Y， HOU Q， JIN H. The Able-Zeilberger algorithm [J].Electron J Comb， 2011， 8: 17．

[6] SUN Z H. Congruences concerning Bernoulli numbers and Bernoulli polynom-ials[J].Discrete Appl Math， 2000， 105: 193-223．

[7] SUN Z W， TAURASO R. New congruences for central binomial coefficients [J]. Adv in Appl Math， 2010， 45: 125-148．

[8] SUN Z W. A new series for π3and related congruences [J]. Internat J Math， 2015， 26(8): 1-23．

[9] SPIESS J. Some identities involving harmonic numbers [J]. Math Comput， 1990， 55: 839-863．

[10] CHYZAK F. An extension of Zeilbergers fast algorithm to general holonomic functions[J]. Discrete Math， 2000， 217: 115-134．

[11] MESTROVIC R. Proof of a congruence for harmonic numbers conjectured by Z.-W. Sun[J]. Int J Number Theory， 2012，8(4):1-5．

2017-02-24.

国家自然科学基金青年基金项目(11601543，11601216)；河南省科技攻关(国际科技合作)项目(172102410069)；河南省高等学校重点科研项目(16B110009)；河南省高等学校青年骨干教师培养计划项目(2015GGJS-115)；洛阳师范学院青年基金项目(2013-QNJJ-001).

1000-1190(2017)03-0277-05

一类含有调和数的同余式

杨继真1， 王云鹏2

(1.洛阳师范学院 数学科学学院， 河南 洛阳， 471934； 2.洛阳理工学院 数理部， 河南 洛阳， 471022)

该文目的是创建一系列含有调和数的同余式.当p>3为一素数时，利用已有的组合恒等式和同余式，得到了如下的同余式：

同时也得到了

这里Bn(n∈)称为Bernoulli数，当pa时，qp(a)=(ap-1-1)/p称为Fermat商.

同余式； 调和式； 组合恒等式

O156.1

A

*通讯联系人. E-mail: wangruipeng1981@126.com.